Lo que hay detrás de la constante de Feigenbaum

Obituario: Mitchell Feigenbaum, (1944-2019), 4.66920160910299067185320382 ...

Artículo del blog de Steven Wolfram



Se llama constante de Feigenbaum y equivale aproximadamente a 4,6692016. Y ocurre con una periodicidad envidiable en ciertos tipos de sistemas matemáticos y físicos que pueden demostrar un comportamiento caótico.

Mitchell Feigenbaum , quien nos dejó el 30 de junio a la edad de 74 años, fue la persona que lo descubrió, en 1975, y lo hizo haciendo matemáticas experimentales en una calculadora de bolsillo.

Este descubrimiento se ha vuelto decisivo en la teoría del caos . Pero cuando se descubrió por primera vez, este resultado fue inesperado, extraño, sin relación con nada de lo que se estudió anteriormente. Sin embargo, de alguna manera, el hecho de que fue Mitchell Feigenbaum quien me descubrió durante casi 40 años descubrió que parece apropiado.

Mitchell, que estudió física teórica y era un conocedor de sus tradiciones matemáticas, siempre parecía considerarse un extraño. Se parecía un poco a Beethoven, e hizo una elegante impresión de cierto secreto intelectual. A menudo hacía declaraciones fuertes, generalmente con una mirada conspirativa, con un brillo en los ojos y una copa de vino o un cigarrillo en la mano.

Hablaba en largas oraciones adornadas que traicionaban erudición e intelectuales en él. Pero las ideas de la misma fueron las más diferentes. A veces eran detallados y técnicos. A veces, estos eran saltos de intuición, que, al menos, no podía seguir. Siempre leía algo, no dormía hasta 5-6 horas, llenaba las páginas amarillas de los cuadernos con fórmulas y cargaba el sistema Mathematica con complejos cálculos algebraicos que podían durar horas.

Publicó poco y los trabajos publicados a menudo lo decepcionaron con el hecho de que no mucha gente los entendía. En el momento de su muerte, había trabajado durante muchos años en la óptica de la percepción y en preguntas como "por qué la luna parece más grande cuando está por encima del horizonte". Sin embargo, no decidió publicar algo así.

Durante más de 30 años, el trabajo oficial de Mitchell (que recibió, de hecho, debido a la apertura de la constante Feigenbaum) fue un profesor en la Universidad Rockefeller en Nueva York (para cumplir con la misión de investigación biológica del Instituto, fue nombrado jefe del "Laboratorio de Física Matemática"). Sin embargo, todavía hizo mucho trabajo, dio su nombre a la puesta en marcha de la informática financiera y estuvo estrechamente asociado con la invención de nuevos métodos cartográficos para el atlas global Hammond .

Lo que Mitchell descubrió

La idea básica es bastante simple. Tome el número x de 0 a 1. Reemplazaremos gradualmente x con ax (1 - x). Supongamos que comenzamos con x = 1/3, y a = 3.2. Luego, aquí están los valores secuenciales de x que obtendremos:



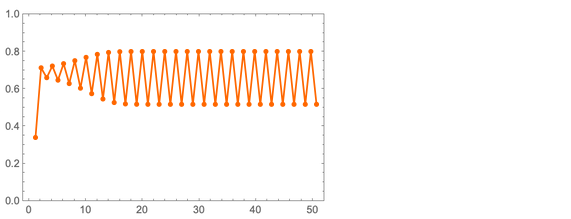
Los valores de x rápidamente se vuelven periódicos, con un período de 2. Pero, ¿qué sucede si tomamos otros valores de a? Aquí hay algunos resultados para el llamado "Mapeo logístico":



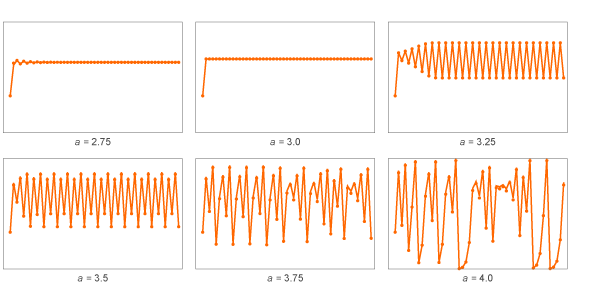
Para a pequeño, los valores de x rápidamente llegan a valores fijos. Para grandes a, se vuelven periódicos, primero con un período de 2, luego 4. Y para grandes a, los valores comienzan a saltar de una manera aparentemente aleatoria.

Esto se puede resumir construyendo los valores de x (aquí hay 300, después de descartar los primeros 50) en función del valor de a:



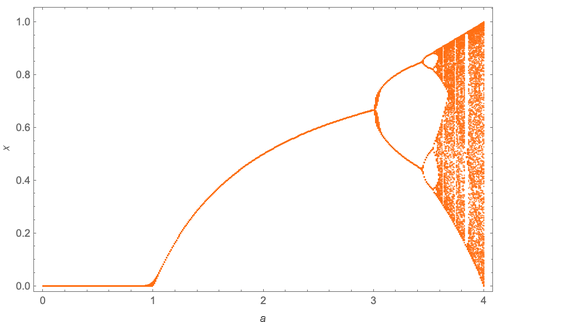
Con el aumento de a, se observa una cascada de duplicación del período. En este caso, ocurren en a = 3, a ≈ 3.449, a ≈ 3.544090, a ≈ 3.5644072. Mitchell señaló que estos valores consecutivos tienen un límite (a _∞ ≈ 3.569946) en la secuencia geométrica, a _∞ - a _n ~ δ ^-n y δ ≈ 4.669.

Un resultado interesante Pero esto es lo que le da sentido: esto es cierto no solo para un cierto mapeo iterativo x → ax (1 - x); Esto es cierto para cualquier pantalla. Aquí, por ejemplo, está el "diagrama de bifurcación" para x → a sin (π √x):



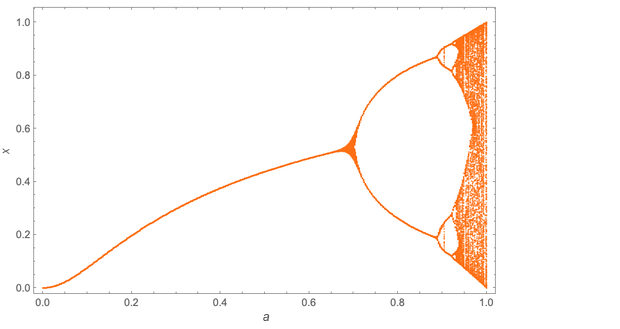
Los detalles difieren, pero Mitchell señaló que la disposición de duplicación del período nuevamente forma una secuencia geométrica con exactamente la misma base δ ≈ 4.669.

Y no solo estos diversos mapeos iterativos dieron resultados cualitativamente similares; cuando se mide la tasa de convergencia, resulta ser exactamente el mismo, siempre δ ≈ 4.669. Este fue el gran descubrimiento de Mitchell: una característica cuantitativamente universal del enfoque del caos en la clase de sistemas.

Antecedentes científicos

La idea básica de los mapeos iterativos tiene una larga historia que se remonta a la antigüedad. Sus primeras versiones surgieron en relación con la búsqueda de aproximaciones sucesivas, por ejemplo, de raíces cuadradas. Por ejemplo, el método de Newton del siglo XVII √2 se puede obtener mediante iteraciones x → 1 / x + x / 2. A partir de x = 1:



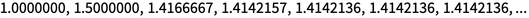
La idea de una aproximación iterativa de una función arbitraria se formalizó por primera vez, aparentemente, en el artículo de 1870 de Ernst Schroeder (conocido por formalizar muchas cosas, desde grados hasta álgebra booleana), aunque la mayoría de las discusiones se referían a la solución de ecuaciones funcionales y no a las iteraciones en sí mismas (excepto el estudio áreas de convergencia de la aproximación newtoniana realizada por Arthur Cayley en 1879). En 1918, Gaston Maurice Julia realizó un extenso estudio de las funciones iterativas de materiales en el plano complejo, inventando el conjunto de Julia . Pero antes de la aparición de los fractales a fines de la década de 1970 (que pronto condujo a la aparición del conjunto de Mandelbrot ), esta área de las matemáticas vegetaba.

Pero independientemente de la investigación en matemática pura, las asignaciones iterativas con formas similares a x → ax (1 - x) comenzaron a aparecer en la década de 1930 entre posibles modelos prácticos para estudiar la biología de la población o la teoría de los ciclos económicos. Por lo general, aparecían en forma de versiones discretas de ecuaciones continuas, como la ecuación logística Verhulst de mediados del siglo XIX. El comportamiento oscilatorio también era común, y en 1954, William Ricoeur (uno de los fundadores de la pesca científica) también encontró un comportamiento más complejo al recorrer las curvas empíricas de reproducción de peces.

En matemática pura, las variantes de mapeos iterativos surgieron periódicamente en la teoría de números. En 1799, Karl Friedrich Gauss , de hecho, estudió el mapeo x → frac (1 / x) en relación con las fracciones continuas. Desde finales del siglo XIX, ha aparecido interés en las asignaciones de la forma x → frac (ax) y su relación con las propiedades de a.

Inmediatamente después del trabajo de Henri Poincaré sobre métodos efectivos de mecánica celeste en la década de 1900, apareció la idea de la sensibilidad a las condiciones iniciales, y al final se notó que los mapas iterativos pueden, de hecho, "desenterrar números" en condiciones iniciales. Por ejemplo, iterar x → frac (10 x) sobre dígitos π esencialmente solo cambia la secuencia de dígitos una posición a la izquierda con cada paso:





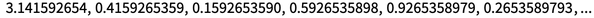
Las asignaciones del tipo x → ax (1-x) también demuestran una "excavación de números" similar (por ejemplo, si x se reemplaza por sin (π u) ² , entonces x → 4 x (1-x) se convierte exactamente en u → frac (u , 2), y esto se conocía en la década de 1940; por ejemplo, John von Neumann comentó esto en 1949 en relación con su método iterativo de cuadrado medio para generar números pseudoaleatorios por una computadora.

Sin embargo, ¿qué pasa con las matemáticas experimentales basadas en mapeos iterativos? Prácticamente no había matemática experimental en las primeras computadoras digitales (el tiempo de la computadora de la mayoría de ellas era demasiado costoso). Pero a raíz del proyecto de Manhattan en Los Alamos, crearon su propia computadora MANIAC, que finalmente comenzó a usarse para una serie de estudios en el campo de las matemáticas experimentales. En 1964, Paul Stein y Stan Ulam escribieron un informe titulado "Estudio de transformaciones no lineales en computadoras electrónicas", que muestra fotografías de pantallas MANIAC similares a las de los osciloscopios y que muestran pantallas iterativas de una forma bastante compleja. En 1971, otro informe creado en Los Alamos "por pura curiosidad" (escrito por Nick Metropolis, el jefe del proyecto MANIAC y el desarrollador del método Monte Carlo, así como Paul Stein y su hermano Miron Stein), produjo resultados computacionales más específicos para mapeos logísticos , y señaló el fenómeno básico de duplicación del período (los autores lo llamaron la secuencia U), así como la resistencia cualitativa a los cambios del método de visualización subyacente.

Aparte de todo esto en física y matemáticas, hubo otros desarrollos. En 1964, Ed Lorenz (meteorólogo del MIT) introdujo y creó una simulación de sus ecuaciones diferenciales "naturales" de su nombre, donde se demostró sensibilidad a las condiciones iniciales. Desde la década de 1940, se ha formado una corriente continua de desarrollos matemáticos en la teoría de los sistemas dinámicos (el trabajo se basó en los logros de Poincare de la década de 1900). En particular, investigaron las propiedades globales de las soluciones de ecuaciones diferenciales. Por lo general, los investigadores encontraron puntos fijos, a veces limitan los ciclos. Sin embargo, en la década de 1970, especialmente después de la aparición de las primeras simulaciones por computadora (como en Lorentz), quedó claro que algo más podría suceder con ecuaciones no lineales: la llamada " Atractor extraño ". Y mientras estudiaba las "asignaciones devueltas" de atractores extraños, las asignaciones iterativas comenzaron a aparecer nuevamente.

Sin embargo, no fue hasta 1975 que varios estudios de mapeos iterativos comenzaron a cruzarse. En el campo de las matemáticas puras, el teórico de sistemas dinámicos Jim York y su alumno Tien-Yen Lee de la Universidad de Maryland publicaron el trabajo "El caos se desprende del período tres", donde mostraron que un mapeo iterativo con un cierto valor de parámetro, cuya condición inicial conduce a la aparición de un ciclo de longitud tres , debe haber otras condiciones iniciales que no conduzcan a la aparición de ciclos o, como lo describen, a demostrar el caos. Luego resultó que Alexander Sarkovsky, un representante de la escuela soviética de investigación de sistemas dinámicos, en 1962, demostró un resultado ligeramente más débil, en el que los ciclos con todos los períodos se siguen de un ciclo con el período 3.

Al mismo tiempo, el interés por los especialistas en biología de la población orientados a las matemáticas comenzó a crecer en los mapeos logísticos, de donde nació la bien escrita revisión de 1976 "Modelos matemáticos simples con dinámicas muy complejas", escrita por un físico australiano educado por Robert May , quien en ese momento era profesor biología en Princeton (luego se convertirá en el asesor científico del gobierno británico y recibirá el título de Barón May de Oxford).

Pero aunque había cosas como bocetos de diagramas de bifurcación, el descubrimiento de sus propiedades numéricas universales tenía que esperar la aparición de Mitchell Feigenbaum.

El viaje de Mitchell

Mitchell Feigenbaum creció en Brooklyn, Nueva York. Su padre era químico analítico y su madre enseñaba en una escuela pública. A Mitchell no le gustaba particularmente estudiar, aunque recibió buenas calificaciones en los exámenes de matemáticas y ciencias exactas, y también aprendió matanálisis y tocó el piano de forma independiente. En 1960, a la edad de 16 años, él, como un niño prodigio, ingresó a la universidad de la ciudad de Nueva York, oficialmente para estudiar ingeniería eléctrica, pero también asistió a cursos de física y matemáticas. Después de graduarse en 1964, ingresó al MIT. Al principio quería defender un doctorado en ingeniería eléctrica, pero rápidamente cambió a física.

Y aunque estaba encantado con la física matemática clásica (como la presentada, por ejemplo, en los libros de Landau y Lifshitz), al final escribió una disertación sobre el tema designado por su curador: física de partículas y una evaluación de la clase de diagramas de Feynman para dispersar fotones por partículas escalares . La disertación no fue muy interesante, pero en 1970 fue enviado a la Universidad de Cornell como postdoctorado.

Mitchell comenzó a tener problemas con la motivación y, en lugar de hacer física, prefería pasar tiempo en cafés, resolviendo crucigramas en el New York Times (que logró hacer con gran velocidad). Pero en Cornell, Mitchell hizo algunos amigos importantes. Uno de ellos era Predrag Tsvitanovic, un destacado estudiante graduado de esa parte de Yugoslavia que ahora se llama Croacia; estudió electrodinámica cuántica y compartió con Mitchell un interés en la literatura alemana. Otra fue la joven poetisa Kathleen Durish (que más tarde se convirtió en Katie Hammond), una amiga de Predrag. Otro fue la estrella en ascenso de la física, el profesor Pete Carruthers, quien compartió con Mitchell un interés por la música clásica.

A principios de la década de 1970, se acercaba la edad de oro de la teoría cuántica de campos. Pero, a pesar del tema de su trabajo, Mitchell no hizo esto, y después de dos años en Cornell no produjo ningún resultado. Sin embargo, logró impresionar a Hans Bethe , y lo transfirió a otro lugar, también como postdoctorado, pero a un instituto que ocupa un lugar un poco más bajo en la jerarquía no oficial: el Politécnico de Virginia.

En el Virgin Institute, Mitchell hizo incluso menos que en Cornell. Prácticamente no se comunicaba con las personas y solo daba un trabajo en tres páginas: "La relación del coeficiente de normalización y la función de dispersión en la ecuación de transporte de multigrupos". Como su nombre lo indica, el trabajo fue técnico y poco interesante.

Al final de los dos años de estadía de Mitchell en Virginia, no estaba claro qué vendría después. Sin embargo, la suerte intervino. El amigo de Mitchell de Cornell, Pete Carruthers, fue contratado para establecer una unidad teórica en Los Alamos, y se le dio carta blanca para contratar a varios físicos jóvenes prominentes. Luego, Pete me dijo con orgullo (como parte del consejo de gestión científica) que tenía la sensación de que Mitchell era capaz de hacer algo grandioso y, a pesar de las opiniones de otras personas, y de la evidencia, decidió ponerlo sobre él.

Tras transferir a Mitchell a Los Alamos, Pete comenzó a ofrecerle proyectos. Al principio fue una continuación del trabajo de Pete, los intentos de calcular un conjunto de propiedades colectivas ("transporte") de la teoría del campo cuántico para comprender las colisiones de partículas de alta energía: estos fueron trabajos que precedieron a los estudios de plasma de quark-gluón.

Pero pronto, Pete sugirió que Mitchell lidiara con la turbulencia en los líquidos, en particular, para averiguar si los métodos del grupo de renormalización ayudarían en este asunto.

Cuando un líquido, por ejemplo, el agua, comienza a fluir lo suficientemente rápido, aparecen pequeños remolinos en él y comienza a comportarse de manera compleja y, a primera vista, de manera aleatoria. Pero aunque este fenómeno se ha discutido cualitativamente durante muchos siglos (por ejemplo, incluso Leonardo da Vinci hizo sus bocetos), los físicos pudieron decirlo notablemente poco, aunque en la década de 1940 Andrei Nikolaevich Kolmogorov hizo un comentario de que los remolinos deberían formar una cascada con k - distribución de energía. En Los Alamos, los científicos se centraron en desarrollar armas atómicas (lo que inevitablemente implica estudiar el comportamiento de los fluidos con fuertes corrientes), y la turbulencia fue muy importante de entender, aunque no era obvio cómo abordarla.

En 1974, aparecieron noticias de que Kenneth Wilson de Cornell "resolvió el problema de Kondo" [el problema de Kondo es la incapacidad de la física teórica para explicar el efecto Kondo / aprox. trans.] utilizando una técnica llamada "grupo de renormalización". Pete Carruthers sugirió que Mitchell aplicara esta técnica a las turbulencias.

El grupo de renormalización está relacionado con cómo el cambio de escala (u otros parámetros) afecta la descripción (y el comportamiento) de los sistemas. Dio la casualidad de que el doctor de Mitchell del MIT, Francis Lowe, junto con Murray Gel-Mann, lo reintrodujo en 1954 en el contexto de la electrodinámica cuántica. La idea permaneció inmóvil durante muchos años, pero surgió en la década de 1970 y se aplicó activamente, aunque de diferentes maneras, tanto a la física de partículas (especialmente a la cromodinámica cuántica ) como a la física de la materia condensada.

En una pieza de hierro en la habitación, puede alinear los espines de todos los electrones asociados con cada átomo, y luego el hierro se magnetizará. Pero si calienta el hierro, las fluctuaciones comienzan en él y, de repente, a una temperatura superior a la llamada. Puntos Curie (770 ° C para el hierro): aparece tanta aleatoriedad en el hierro que desaparecen sus propiedades magnéticas. En general, hay bastantes situaciones (derretimiento, ebullición, formación de congestión de tráfico) cuando este repentino llamado transición de fase

Pero, ¿qué sucede exactamente durante la transición de fase? Creo que la forma más fácil de ver esto es estudiando su contraparte en el campo de los autómatas celulares. Con una cierta regla, dada a continuación, cuando el sistema inicialmente no tiene una gran cantidad de celdas negras, pronto todo se volverá blanco. Pero si aumenta el número de células negras originales (por analogía con el aumento de la temperatura del sistema magnético), de repente, en este caso, con una proporción del 50% de células negras, se produce una transición brusca, y todo el sistema finalmente se vuelve negro (observación para expertos en transiciones de fase: sí , esta es una transición de fase en un sistema unidimensional; solo se puede necesitar una bidimensional si el sistema necesita ser microscópicamente reversible ).



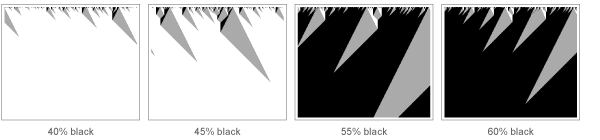
Pero, ¿qué le sucede al sistema cerca del borde del 50% de las células negras? De hecho, ella no puede decidir si se vuelve negra o blanca. Como resultado, muestra una jerarquía completa de fluctuaciones, desde la más pequeña hasta la más grande. En la década de 1960, quedó claro que los "exponentes críticos" que caracterizan las leyes de poder que describen estas fluctuaciones son los mismos para muchos sistemas.

Pero, ¿cómo calculamos estos exponentes críticos? En algunos casos artificiales, se conocían métodos analíticos. Pero en su mayor parte, se requería algo más.A finales de la década de 1960, Ken Wilson se dio cuenta de que podían usarse grupos de renormalización y computadoras. Es posible construir un modelo para la interacción de giros individuales. Pero el grupo de renormalización le ofrece un procedimiento de "escala" para las interacciones de más y más bloques grandes de giros. Y al estudiar esto en una computadora, Ken Wilson logró comenzar a calcular exponentes críticos.

Al principio, los físicos no prestaron la debida atención a esto, sobre todo porque no estaban acostumbrados a un uso tan activo de las computadoras en física teórica. Pero entonces apareció el problema de Kondo. En la mayoría de los materiales, la resistencia eléctrica disminuye al disminuir la temperatura (y en los superconductores disminuye a cero incluso a temperaturas superiores al cero absoluto). Sin embargo, en la década de 1930, las mediciones en oro mostraron que su resistencia aumenta a bajas temperaturas. En la década de 1960, se creía que todo se trataba de la dispersión de electrones por impurezas magnéticas; sin embargo, los cálculos tuvieron problemas, dando infinidad en los resultados.

Luego, en 1975, Ken Wilson aplicó sus métodos de grupo de renormalización y pudo calcular con precisión el efecto. Este efecto todavía está envuelto en algún misterio (probablemente debido al hecho de que a menudo tuve dificultades para comprender las explicaciones de Ken Wilson sobre este tema, al menos desde que lo conocí en la década de 1980). Pero la idea de que el grupo de renormalización puede ser importante ha echado raíces.

¿Cómo se puede aplicar a la turbulencia de fluidos? La ley de poder de Kolmogorov dio ciertas ideas. ¿Pero fue posible tomar las ecuaciones de Navier-Stokes que controlan el flujo de un fluido idealizado y derivar alguna de ellas? Este proyecto fue asumido por Mitchell Feigenbaum.

Descubrimiento importante

Es muy difícil trabajar con las ecuaciones de Navier-Stokes. Hasta el día de hoy no está muy claro cómo incluso la propiedad más obvia de la turbulencia, su aparente aleatoriedad, surge de ellos. Quizás estas ecuaciones no son una descripción matemática completa o consistente, y en realidad vemos movimientos microscópicos mejorados de las moléculas. Quizás, como en la teoría del caos y las ecuaciones de Lorentz, todo se trata de mejorar la aleatoriedad en las condiciones iniciales. Personalmente, basado en mi trabajo de la década de 1980, creo que todo el punto está en las propiedades de sus cálculos internos, similar a la aleatoriedad en mi " regla 30 " para un autómata celular.

¿Cómo abordó Mitchell este problema? Intentó simplificarlo: primero pasando de ecuaciones que dependen del espacio y el tiempo a ecuaciones que dependen solo del tiempo, y luego haciéndolas discretas y estudiando mapeos iterativos. De Paul Stein, Mitchell estaba al tanto de trabajos previos sobre mapeos iterativos realizados en Los Alamos (que no era ampliamente conocido). Pero Mitchell no entendió qué camino seguir, aunque, después de haber recibido a su disposición una nueva calculadora programable ultramoderna HP-65, decidió programar pantallas iterativas en ella.

Luego, en julio de 1975, Mitchell fue a una reunión física de verano en Aspen, Colorado. Allí se reunió con Stephen Smale, un famoso matemático que estudió sistemas dinámicos, y se sorprendió al saber que estaba hablando de mapeos iterativos. Smale mencionó que alguien le preguntó si el límite de una cascada con un período de duplicación a _∞ ≈ 3.56995 se puede expresar en términos de constantes estándar como π y √2. Smale no sabía la respuesta a esta pregunta. Sin embargo, Mitchell se interesó en esto y decidió tratar de encontrar la respuesta.

No tenía el HP-65 con él, pero se sumergió en este problema utilizando herramientas estándar de un físico matemático educado, y pronto convirtió la tarea en una búsqueda de polos de función en el plano complejo, del que no tenía nada que decir. Sin embargo, volviendo a la de Los Álamos, en agosto, se volvió a su HP-65 y lanzó su programación con el fin de detectar a los puntos de bifurcación _n .

Para n pequeña, la iteración fue bastante rápida. Para n = 5, tardó 30 segundos. Para n = 6, ya tuve que esperar varios minutos. Sin embargo, mientras la calculadora funcionaba, Mitchell decidió mirar los valores de una _n que ya tenía, y notó algo: parecían esforzarse geométricamente por algún valor final.

Al principio, simplemente utilizó este hecho para estimar un _∞ , que, a pesar de todos los intentos, no pudo expresar a través de constantes estándar. Pero pronto comenzó a sospechar que el exponente de convergencia δ era más importante que un _∞ , ya que su valor se mantuvo sin cambios con cambios simples en las variables en el mapa. Durante aproximadamente un mes, Mitchell intentó expresar δ en términos de constantes estándar.

Pero luego, en octubre de 1975, recordó que Paul Stein dijo que duplicar un período se ve igual no solo para las asignaciones logísticas, sino en general para todas las asignaciones iterativas con un máximo. Después de reunirse con su HP-65 después de un viaje a Caltech, Mitchell inmediatamente probó la pantalla x → sin (x) y descubrió que, con hasta tres decimales, el exponente δ era exactamente el mismo.

Inmediatamente decidió que había tropezado con algo maravilloso. Pero Stein dijo que necesitaría más números para sacar conclusiones. Había muchas computadoras potentes en Los Alamos, por lo que al día siguiente Mitchell le pidió a alguien que le mostrara cómo escribir un programa FORTRAN para continuar, y al final del día pudo calcular que en ambos casos δ tenía un valor de aproximadamente 4.6692 .

La computadora que usaba era un caballo de batalla típico para la ciencia estadounidense en esos días: el modelo CDC 6000 (el mismo tipo que usé cuando me mudé a los Estados Unidos en 1978). Fue desarrollado por Seymour Cray y, por defecto, utilizó números de coma flotante de 60 bits. Pero con tal precisión (14 dígitos después del punto decimal) Mitchell no pudo obtener nada mejor que 4.6692. Afortunadamente, la esposa de Pete, Lucy Carruthers, era programadora de Los Alamos, y le mostró a Mitchell cómo usar la precisión doble. Como resultado, pudo calcular δ hasta 11 decimales y determinar que los valores de dos asignaciones iterativas diferentes son iguales.

En el transcurso de varias semanas, Mitchell descubrió que δ parece ser un valor universal para todos los mapas de iteración con un máximo cuadrático. Pero no sabía por qué estaba sucediendo esto, y no tenía ningún aparato matemático específico para estudiar este tema. Pero al final, a la edad de 30 años, Mitchell descubrió algo que le pareció realmente interesante.

En su cumpleaños el 19 de diciembre, Mitchell se reunió con su amigo Predrag y le contó sobre este resultado. Sin embargo, en ese momento, Predrag estaba trabajando con la física de partículas convencional, y no le dio mucha importancia a esto.

Mitchell continuó trabajando, y después de unos meses se convenció de que no solo el exponente δ era universal, con la escala adecuada, las asignaciones iterativas en sí mismas eran universales. En abril de 1976, Mitchell escribió un informe sobre sus hallazgos. El 2 de mayo de 1976, habló sobre ellos en una conferencia en el Instituto de Investigación Avanzada de Princeton. Predrag estaba allí, y luego finalmente se interesó en el trabajo de Mitchell.

Pero Predrag a menudo no tenía claro de qué estaba hablando Mitchell. Pero al día siguiente, Predrag logró simplificar la tarea y obtener una ecuación funcional inmediata para la forma limitada del mapa de iteración escalado: g (g (x)) = -g (α x) / α, donde α ≈ 2.50290, lo que implica que para cualquier mapeo iterativo de cierto tipo, su forma limitada se verá como una versión más tortuosa de este mapeo:

Cómo se desarrolló todo

El campo de investigación sobre mapeos iterativos ganó impulso el 10 de junio de 1976 después de publicar una revisión en la revista Nature de Robert May, que escribió independientemente de Mitchell y, naturalmente, sin mencionar los resultados que obtuvo. Pero en los meses que siguieron, Mitchell viajó con sus informes sobre sus resultados. La reacción a ellos fue mixta. Los físicos estaban interesados ​​en cómo estos resultados se relacionan con la física. Los matemáticos no entendieron su estado, dado que se obtuvieron de las matemáticas experimentales y no tenían una prueba matemática formal. Y, como siempre, a la gente le costaba entender las explicaciones de Mitchell.

En el otoño de 1976, Predrag obtuvo un postdoc en Oxford, y el primer día que llegué allí, un estudiante de 17 años que escribía un diploma en física de partículas, me reuní con él. Hablamos principalmente sobre su elegante método de "huella de pájaro" para trabajar con la teoría de grupos (cuyo libro finalmente publicó 32 años después). También trató de explicarme mapas iterativos. Y todavía recuerdo cómo habló sobre un modelo idealizado de población de peces en el Adriático (solo después de años lo relacioné con el hecho de que Predrag era de esos lugares que ahora se llaman Croacia).

En ese momento no le di ninguna importancia a esto, pero la idea de mapeos iterativos se arraigó en mi mente, y pronto se mezcló con la idea de fractales, que aprendí del libro de Benoit Mandelbrot . Y cuando, después de un par de años, me concentré en los problemas de complejidad, estas ideas me ayudaron a llegar a sistemas como los autómatas celulares.

Pero en 1976, Mitchell (hasta mi próxima reunión con quien pasarán varios años más) viajó activamente con informes sobre los resultados. También presentó trabajo a la prestigiosa revista científica Advances in Mathematics. Durante seis meses no recibió noticias de allí, pero al final el trabajo fue rechazado. Lo intentó de nuevo, enviando otro trabajo al SIAM Journal of Applied Mathematics, con el mismo resultado.

Quiero decir que esto no me sorprende. En mi experiencia de publicaciones en literatura académica (que no he estado haciendo durante mucho tiempo), publicar un trabajo en un campo de investigación definido es bastante fácil. Pero el trabajo en el campo de algo realmente nuevo u original puede basarse prácticamente en rechazarlo después de una evaluación experta, ya sea por falta de visión intelectual o por corrupción académica. Mitchell tenía otro problema: sus explicaciones eran difíciles de entender.

Pero finalmente, en 1977, Joel Lebovitz, editor del Journal of Statistical Physics, acordó publicar el trabajo de Mitchell, de hecho, porque lo conoció, porque admitió que no entendía el trabajo. Entonces apareció el trabajo de 1978 "Universalidad cuantitativa en la clase de transformaciones no lineales", que describe el gran logro de Mitchell. Para establecer prioridades académicas, Mitchell a veces citó un resumen del informe que hizo el 26 de agosto de 1976 y publicó en la colección anual de informes de la División Teórica de Los Alamos para 1975-1976. Mitchell estuvo muy influenciado por las negativas a publicar sus obras, y durante años mantuvo cartas con negativas en un cajón.

Mitchell continuó viajando por todo el mundo con informes sobre los resultados. Había interés en ellos, pero había desconcierto. Sin embargo, sucedió algo sorprendente en el verano de 1979: Albert Liebhaber de París anunció los resultados de un experimento físico sobre la transición a la turbulencia en los flujos convectivos de helio líquido, donde vio una duplicación del período exactamente con el exponente δ que calculó Mitchell. Resultó ser universal no solo para la clase de sistemas matemáticos, sino que también demostró estar en sistemas físicos reales.

Y al instante Mitchell se hizo famoso. Se descubrió una conexión con el grupo de renormalización, su trabajo se puso de moda tanto para físicos como para matemáticos. Mitchell continuó viajando con informes, pero ahora tuvo la oportunidad de pasar tiempo con los mejores físicos y matemáticos.

Recuerdo cómo llegó a Caltech, en algún momento del otoño de 1979. Todo esto se parecía a una reunión con una estrella de rock. Mitchell llegó, hizo un informe elegante, pero un poco misterioso, y luego Richard Feynman y Murray Gell-Man lo robaron para una conversación privada.

Pronto, a Mitchell le ofrecieron un montón de diferentes trabajos de alto nivel, y en 1982 regresó triunfante a Caltech como profesor de física. Se habló de que el descubrimiento merecía un premio Nobel, y en junio de 1984 apareció en la revista New York Times, con la elegancia de Beethoven, en medio de una cascada de Cornell:



Pero los matemáticos seguían infelices. Como en el caso de Benoit Mandelbrot, consideraron los resultados de Mitchell como "hipótesis numéricas", no probadas e indignas de mención. Sin embargo, los mejores matemáticos (con quienes Mitchell se hizo amigo) pronto comenzaron a trabajar en este problema, y ​​los resultados no tardaron en llegar, aunque tardó diez años en completarse y la prueba final de la universalidad de δ.

¿A dónde fue la ciencia?

¿Qué pasó con el gran descubrimiento de Mitchell? Por supuesto, se hizo famoso. Y las cascadas con período de duplicación con sus propiedades universales pronto se encontraron en varios sistemas: en líquidos, ópticas, etc. ¿Pero cuán comunes eran? ¿Podrían expandirse para cubrir todo el problema de la turbulencia en un fluido?

Mitchell y otros estudiaron sistemas distintos a los mapeos iterativos y encontraron fenómenos relacionados. Pero entre ellos no fue tan sorprendente como el primer descubrimiento de Mitchell.

En cierto sentido, mis intentos de estudiar autómatas celulares y el comportamiento de programas simples, comenzados en 1981, tenían como objetivo buscar algunas de las grandes preguntas a las que el trabajo de Mitchell podría conducir. Sin embargo, nuestros métodos y resultados fueron muy diferentes. Mitchell siempre trató de mantenerse cerca de las cosas a las que los físicos matemáticos tradicionales pueden recurrir, y sin miedo entré en el universo de la computación, explorando los fenómenos encontrados allí.

Traté de entender cómo el trabajo de Mitchell podría estar relacionado con el mío, y en mi primer trabajo sobre autómatas celulares en 1981, incluso noté, por ejemplo, que la densidad promedio de las células negras en pasos sucesivos en la evolución de un autómata celular se puede estimar aproximadamente a través del mapeo iterativo.

También noté que matemáticamente toda la evolución de un autómata celular puede considerarse como un mapa iterativo, aunque no en un conjunto de números reales ordinarios, sino en un conjunto de cantor . En mi primer trabajo, incluso construí un análogo de mapeos suaves de Mitchell, sin embargo, eran salvajes e intermitentes en mí:



Pero, no importa cómo lo intenté, no pude encontrar ninguna conexión obvia con el trabajo de Mitchell. Estaba buscando análogos de la duplicación del período o la orden de Sharkovsky , pero no encontré nada especial. Para mi plataforma informática, incluso pensar en números reales con sus secuencias infinitas de números no era natural. Muchos años después, en el libro "Un nuevo tipo de ciencia", inserté la nota "Mapeo iterativo suave". Mostré su secuencia de números y observé cómo el descubrimiento de Mitchell implica la presencia de una estructura anidada inusual al comienzo de las secuencias:

Fin de la historia

¿Qué le pasó a Mitchell? Después de pasar cuatro años en Cornell, se mudó a la Universidad Rockefeller en Nueva York, y los siguientes 30 años llevaron una existencia casi bohemia, pasando la mayor parte de su tiempo en su departamento en el Upper East Side de Manhattan.

Mientras estaba en Los Alamos, Mitchell se casó con una mujer de ascendencia alemana llamada Cornelia, la hermana del físico (y mi viejo amigo) David Campbell, quien fundó el Centro de Estudios No Lineales en Los Alamos y luego se convirtió en rector de la Universidad de Boston. Sin embargo, bastante rápido, Cornelia dejó Mitchell, y nada menos que a Pete Carruthers. Más tarde, Pete, que sufre de alcoholismo y otros problemas, se reunió con su esposa Lucy, pero murió en 1997 a la edad de 61 años.

En Cornell, Mitchell conoció a Gunilla, quien, a la edad de 14 años, escapó de la familia de un pastor de un pequeño pueblo en el norte de Suecia, y al principio fue modelo con Salvador Dali, y luego llegó a Nueva York en 1966 como modelo de moda. Gunilla era periodista, grabó en video, escribió obras de teatro y pintó cuadros. Se casaron con Mitchell en 1986, y su matrimonio duró 26 años, durante los cuales Gunilla hizo una buena carrera en el arte figurativo .

El último trabajo, escrito por Mitchell por su cuenta, fue publicado en 1987. También publicó muchos trabajos con varios coautores, aunque ninguno de ellos se volvió particularmente notable. La mayoría de ellos continuaron sus primeras investigaciones, o trataron de aplicar los métodos tradicionales de física matemática a varios fenómenos complejos similares al flujo de fluidos.

A Mitchell le gustaba interactuar con los niveles superiores de la academia. Recibió todo tipo de premios y reconocimientos (excepto el Premio Nobel). Pero hasta el final se consideró un extraño: un hombre del Renacimiento que se centró en la física, pero que no creía plenamente en todas las instituciones y prácticas.

Desde principios de la década de 1980, he visto bastante regularmente con Mitchell, en Nueva York y en otros lugares. Usó la plataforma de Mathematica a diario, la elogió y a menudo habló sobre los complejos cálculos que realizó con ella. Al igual que muchos físicos matemáticos, Mitchell era un experto en funciones especiales, y a menudo hablaba conmigo sobre funciones cada vez más exóticas, que, en su opinión, deberíamos agregar al producto.

Mitchell tenía dos pasatiempos principales fuera del campo académico. A mediados de la década de 1980, la joven poetisa, que ahora se llama Katie Hammond, y a quien Mitchell conocía de Cornell, era gerente de publicidad del New York Times y se casó con un hombre de una familia que era propietaria de Hammond World Atlas Publishing House. A través de él, Mitchell se sumergió en un mundo completamente nuevo de cartografía.

Hablé con él sobre este tema muchas veces. Estaba orgulloso de haber descubierto cómo usar el teorema de mapeo de Riemann para obtener mapeos locales especiales al crear mapas. Me describió un algoritmo basado en la física para colocar etiquetas en los mapas (aunque todavía no lo entendía completamente). Estaba muy satisfecho con el lanzamiento de la nueva edición del atlas de Hammond (que más tarde llamó "mi atlas").

Desde la década de 1980, la tendencia de aplicar ideas físicas a las finanzas cuantitativas se ha desarrollado activamente, y los físicos a menudo se convierten en analistas de Wall Street. Y dado que los financieros buscan constantemente beneficios únicos, siempre hay interés en nuevos métodos. A menudo me contactaron con preguntas similares, pero después del éxito del libro de James Gleick "Chaos" de 1987 (sobre el que di una larga entrevista), apareció una multitud de personas que querían saber cómo el "caos" podría ayudarlos a administrar sus finanzas.

Uno de ellos era alguien Michael Gudkin . Al estudiar en la universidad a principios de la década de 1960, fundó una empresa de investigación jurídica para estudiantes de derecho. Unos años más tarde, contrató a varios economistas que ganaron el Premio Nobel, y fundó, quizás, el primer fondo de cobertura para tratar el comercio de arbitraje utilizando computadoras. Gudkin fue una moto toda su vida, le encantaban los juegos de azar, los viajes y el backgammon, y ganaba mucho dinero. En uno de los momentos desafortunados, estaba buscando una nueva solución, y descubrió la teoría del caos y Mitchell Feigenbaum.

Trabajó en varios físicos durante varios años, y luego, en 1995, formó un equipo y fundó la compañía Numerix para comercializar el uso de métodos de cálculo físico en el campo de instrumentos financieros cada vez más exóticos. Mitchell Feigenbaum era el rostro de la empresa, aunque mi viejo amigo Nigel Goldenfield y su joven colega Sasha Sokol llevaron todo el trabajo duro.

Desde el principio, la compañía tuvo mucho trabajo relacionado con la física matemática, y Mitchell participó activamente en ella. Era un gran amante del cálculo estocástico de Ito, dio conferencias sobre él y estaba orgulloso de haber encontrado un método para acelerar la integración estocástica mil veces. Sin embargo, la compañía realmente escribió bibliotecas en C ++ para su integración en sistemas bancarios. Mitchell no quería hacer algo así a la larga. Después de varios años de trabajo, su actividad en la empresa disminuyó.

Me reuní con Gudkin en 1998, y luego 14 años después. Poco antes de eso, escribió una autobiografía, "La respuesta incorrecta para ser más rápido: una historia confidencial de crear una máquina de billones de comercio", y de repente se puso en contacto conmigo, invitándome a participar en un nuevo negocio oscuro. Mitchell todavía hablaba bien de Michael, aunque cuando de repente se habló de que fundé una nueva compañía y me convertí en su director, me negué.

Todos estos años, a menudo hablé con Mitchell, aunque nuestros contactos no estaban tan bien conservados en el archivo como podrían estarlo, porque le gustaba hablar más por voz que por correo. Él me escribió una vez: “No me gusta que me correspondan por correo electrónico. Todavía prefiero escuchar la voz e interactuar con la persona ".

Pero algunos fragmentos se conservaron en mi archivo. Hay, por ejemplo, correspondencia sobre el cumpleaños número 60 de Mitchell en 2004, que no pude, porque se cruzó con el cumpleaños de uno de mis hijos. En cambio, ordené la producción del Cristal Feigenbaum-Zvitanovich, una escultura de vidrio tridimensional que representa la restricción de la función g (z) en el plano complejo.

Resolver la ecuación funcional fue un poco difícil, y el grabado con láser primero dividió un par de bloques de vidrio, pero al final este objeto fue hecho y enviado, y muchos años después me complació verlo en un estante en el departamento de Mitchell:



A veces, en mis archivos, menciones de Mitchell aparecen por otras personas, generalmente por el Predrag. En 2007, Predrag me escribió (con su característico sentido del humor):

Para otras noticias: acaba de conocer a Mitchell, se encuentra con Odyssey.

No me refiero a un costoso servicio de acompañantes, sino a Homer Odyssey. Comenzó a calcular la ubicación de las estrellas en función de una precesión de 26,000 años. Él dice que Hiparco alguna vez calculó todo esto, pero la Iglesia Católica logró destruir todas las copias de sus tabletas ".

Justificando su imagen como un hombre del Renacimiento, Mitchell siempre estuvo seriamente interesado en la historia. En 2013, en respuesta a mi artículo sobre Leibniz, Mitchell dijo que había sido un amante de Leibniz desde la adolescencia y explicó:

"El hagiógrafo de Newton, Voltaire, no tenía idea de la esencia de la monadología , por lo que solo podía fingir" el mejor de todos los mundos posibles ". Hace mucho tiempo publiqué esto como un medio oral para explicar la universalidad de 2 ⁿ .

El segundo de los trabajos de Leibniz, publicado cuando tenía 19 años, "Sobre métodos de inversión de tangente", o algo así, contenía la invención del método de isoclina para resolver ecuaciones diferenciales ordinarias. Leibniz y Newton comienzan con ecuaciones diferenciales, ya que han recibido notación diferencial. Una historia muy interesante ".

Sin embargo, la física matemática siempre ha sido una fortaleza de la vida intelectual de Mitchell, aunque más a nivel personal que como parte de su trabajo académico. En algún momento, su ahijada, siendo muy joven, le preguntó por qué la luna, al estar más cerca del horizonte, parece ser más grande. Él le escribió una respuesta (un poco como las cartas de Euler a una princesa alemana), y luego se dio cuenta de que no estaba seguro de la respuesta, y se embarcó en muchos años de investigación en óptica e imagen. Una vez en el MIT, se interesó en el trabajo de la retina, inspirado en el libro de Jerry Lettwin "Lo que el ojo de la rana le dice al cerebro de la rana".

Me contó sobre esto, diciendo que la teoría habitual de la formación de imágenes está equivocada y que tiene una teoría mejor. Siempre usó el tamaño de la luna como ejemplo, pero no estaba seguro de si este problema estaba relacionado con la óptica o la percepción. Nunca publicó trabajos relacionados con este tema, aunque con suerte sus manuscritos (según los rumores, estaba preparando un libro), como resultado verán la luz, si alguien más puede entenderlos.

Cuando visité Mitchell y Gunilla, sus apartamentos causaron una impresión bohemia: había libros, papeles, pinturas y varias cosas similares en todas partes. Y había un pájaro. Era una cacatúa y era ruidosa. No sé quién y por qué lo trajo. Pero era bastante problemático. Mitchell y Gunilla casi fueron expulsados ​​del departamento debido a las quejas de los vecinos sobre el ruido, y finalmente llevaron al Bird a los médicos. Como descubrí más tarde, al revisar inesperadamente el plan nunca implementado para desarrollar videojuegos para mascotas ("la mente de otra persona en nuestro planeta"), las cacatúas son criaturas sociales, y esas mascotas definitivamente necesitan un "twitter para la cacatúa".



Como resultado, Gunilla dejó a la familia y, según los rumores, fue por el Pájaro.

La última vez que nos encontramos con Mitchell en persona hace unos años. Mi hijo Christopher y yo fuimos a visitarlo, y estaba emocionado como Mitchell, con los ojos brillantes, habló rápidamente y un poco misteriosamente sobre el tema de la física matemática de la formación de imágenes. "Los ojos de los pájaros están sobrevalorados", dijo al sonido de su cacatúa desde la habitación de al lado. Su fosa central es muy pequeña. Sus ojos funcionan como telescopios.

"Los ojos de los peces son los mejores", dijo, explicando que todos los ojos aparecieron como resultado de la evolución bajo el agua, y su arquitectura no ha cambiado mucho desde entonces. "Los peces mantienen todo el campo de visión enfocado, a diferencia de nosotros", dijo. Era encantador, excéntrico y muy Mitchell.

Durante años, hablamos periódicamente por teléfono, generalmente a última hora de la tarde. Hace unos meses conocí a Predrag y le dije que estaba sorprendido de no haber hablado con Mitchell durante mucho tiempo. Explicó que Mitchell estaba enfermo, pero no se lo contó a nadie. Hace unas semanas, alrededor de la medianoche, Predrag me envió un correo electrónico con el tema "Mitchell está muerto", explicando que Mitchell murió alrededor de las 8 p.m. y adjuntó a la carta una fotografía típica de "Mitchell en Nueva York":



A lo largo de los años, he desarrollado un cierto ritual para mí: cuando escucho sobre la muerte de un amigo, inmediatamente empiezo a buscarlo en mis archivos. Y de repente descubrí que hace unos años Mitchell llamó a mi correo de voz, cuya existencia no sospechaba. Así que ahora puedo darle a Mitchell la oportunidad de decir la última palabra .

Y, por supuesto, escriba el último número: 4.66920160910299067185320382 ...