👨🏾‍⚕️ ➰ ⭐️ Cosmología y fluctuaciones cuánticas en el navegador. 👋🏻 🧗🏿 📉

Establezcamos un objetivo puramente práctico: implementar un lienzo sin fin con la capacidad de moverlo y escalarlo con el mouse. Tal lienzo, por ejemplo, puede servir como un sistema de coordenadas en movimiento en un editor gráfico. La implementación de nuestra idea no es tan complicada, pero el proceso de comprensión está asociado con objetos matemáticos y físicos fundamentales, que consideraremos a medida que nos desarrollemos.

Resultado

Declaración del problema.

Desde nuestro lienzo, queremos realizar solo dos funciones: mover el mouse y el movimiento del mouse, así como hacer zoom al desplazarse. La arena de nuestras transformaciones elegirá un navegador. Las armas, en este caso, no tienen que elegir.

Máquina de estado

El comportamiento de tales sistemas se describe convenientemente mediante transiciones entre sus estados, es decir máquina de estado $\ delta: S \ rightarrow S$ donde $\ delta$ - la función de transición entre estados, que muestra muchos estados en sí misma.

En nuestro caso, el diagrama de estado se ve así:

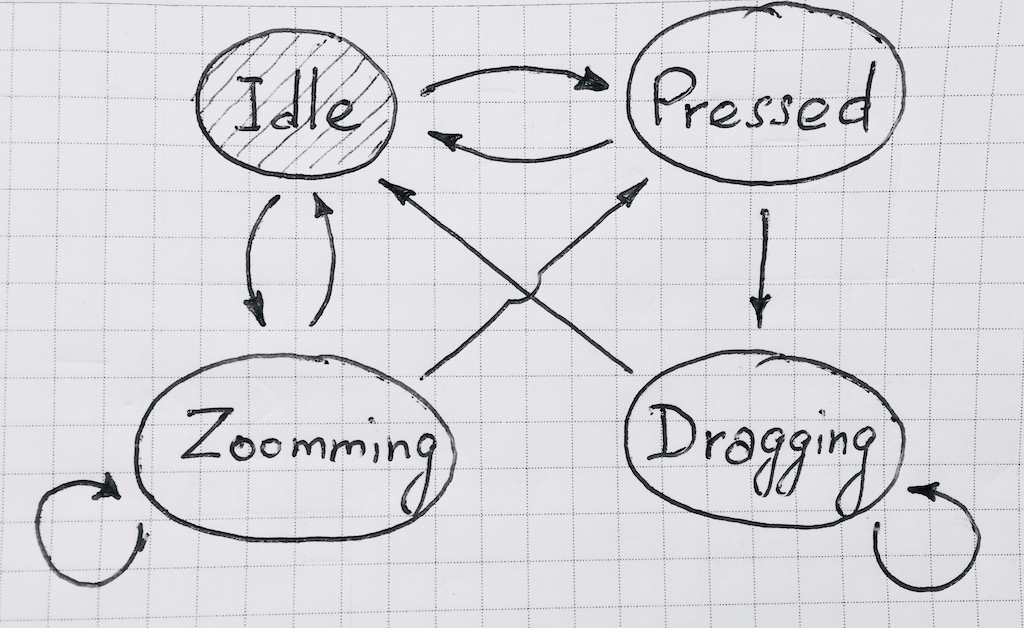
Al implementar la función de transición, es conveniente hacer que el evento sea dependiente. Esto se hará evidente en el futuro. Del mismo modo, es conveniente poder suscribirse a un cambio en el estado de la máquina.

type State = string | number; type Transition<States = State> = { to: States, where: (event: Event) => Array<boolean>, }; type Scheme<States = State> = { [key: States]: Array<Transition<States>> }; interface FSM<States = State> { constructor(state: States, scheme: Scheme<States>): void; // Returns true if the scheme had a transition, false otherwise get isActive(): boolean; // Dispatch event and try to do transition dispatch(event: Event): void; // subscribe on state change on(state: States, cb: (event: Event) => any): FSM<States>; // remove subscriber removeListener(state: States, cb: (event: Event) => any): void; };

Pospondremos la implementación por un tiempo y retomaremos las transformaciones geométricas que subyacen en nuestra tarea.

Geometrías

Si el problema con mover el lienzo es tan obvio que no nos detendremos en él, entonces el estiramiento debe considerarse con más detalle. En primer lugar, requerimos que el estiramiento deje un solo punto estacionario: el cursor del mouse. La condición de reversibilidad también debe cumplirse, es decir La secuencia inversa de las acciones del usuario debe llevar el lienzo a su posición original. ¿Qué geometría es adecuada para esto? Consideraremos un grupo de transformaciones puntuales del plano en sí mismo $\ mathbb {R} ^ 2 \ rightarrow \ mathbb {R} ^ 2$ , que generalmente se expresa mediante la introducción de nuevas variables $x ', y'$ definido como funciones de antaño:

x^{'} = v a r p h i (x, y) y^{'} = p s i (x, y)

$x '= \ varphi (x, y) \\ y' = \ psi (x, y)$

De acuerdo con el principio de dualidad en las matemáticas, tales transformaciones pueden interpretarse como un cambio en el sistema de coordenadas, así como una transformación del espacio en sí mismo con este último fijo. La segunda interpretación es conveniente para nuestros propósitos.

Una comprensión moderna de la geometría es diferente de una comprensión de los antiguos. Según F. Klein , - la geometría estudia invariantes con respecto a ciertos grupos de transformación. Entonces, en un grupo de movimientos $D$ la invariante es la distancia entre dos puntos $d ((x_ {1}, y_ {1}), ((x_ {2}, y_ {2})) = \ sqrt {(x_ {1} - x_ {2}) ^ 2+ (y_ {1 } - y_ {2}) ^ 2}$ . Incluye separación silábica paralela $T _ {(x, y)}$ en vector $(x, y)$ rotación $R _ {\ phi}$ relativo al origen en un ángulo $\ phi$ y reflexiones $M_ {l}$ relativo a alguna línea $l$ . Tales movimientos se llaman elementales. La composición de los dos movimientos pertenece a nuestro grupo y a veces se reduce a primaria. Entonces, por ejemplo, dos reflexiones especulares consecutivas en relación con las líneas rectas $l$ y $n$ dé una rotación alrededor de cierto centro en cierto ángulo (verifíquelo usted mismo):

M_{l} c i r c M_{n} = T_{(- a, - b)} c i r c R_{a l p h a} c i r c T_{(a, b)}

$M_ {l} \ circ M_ {n} = T _ {(- a, -b)} \ circ R _ {\ alpha} \ circ T _ {(a, b)}$

Seguramente ya habrás adivinado que tal grupo de movimientos $D$ forma geometría euclidiana. Sin embargo, el estiramiento no preserva la distancia entre dos puntos, sino su relación. Por lo tanto, un grupo de movimientos, aunque debería incluirse en nuestro esquema, pero solo como un subgrupo.

La geometría que nos conviene se basa en un grupo de estiramiento. $P$ a lo cual, además de los movimientos anteriores, se agrega homotetería $S_ {k}$ por coeficiente $k$ .

Bueno, el ultimo. El elemento inverso debe estar presente en el grupo. Y por lo tanto hay un neutral $e$ (o solo) que no cambia nada. Por ejemplo

S_{k} c i r c S_{k}^{- 1} = e

$S_ {k} \ circ S_ {k} ^ {- 1} = e$

significa primero estirar en

k

$k$ veces y luego en

1 / k

$1 / k$ .

Ahora podemos describir el estiramiento, dejando el punto del cursor del mouse fijo, en lenguaje grupal teórico:

(x, y) r i g h t a r r o w (x, y) (T_{(- c l i e n t X, - c l i e n t Y)} c i r c S_{k} c i r c T_{(c l i e n t X, c l i e n t Y)})

$(x, y) \ rightarrow (x, y) (T _ {(- clientX, -clientY)} \ circ S_ {k} \ circ T _ {(clientX, clientY)})$

Nota 1

En el caso general, la reorganización de las acciones no es conmutativa (primero puede quitarse el abrigo y luego la camisa, pero no al revés).

f o r a l l (x, y) i n m a t h b b R^{2} n e q 0 R i g h t a r r o w T_{(- x, - y)} c i r c S_{k} c i r c T_{(x, y)}) n e q S_{k} c i r c T_{(- x, - y)} c i r c T_{(x, y)})

$\ forall (x, y) \ in \ mathbb {R} ^ 2 \ neq 0 \ Rightarrow T _ {(- x, -y)} \ circ S_ {k} \ circ T _ {(x, y)}) \ neq S_ {k} \ circ T _ {(- x, -y)} \ circ T _ {(x, y)})$

Expresa el movimiento $T _ {(x, y)}$ y $S_ {k}$ y su composición como funciones de un vector en código

 type Scalar = number; type Vec = [number, number]; type Action<A = Vec | Scalar> = (z: Vec) => (v: A) => Vec; // Translate const T: Action<Vec> = (z: Vec) => (d: Vec): Vec => [ z[0] + d[0], z[1] + d[1] ]; // Scale const S: Action<Scalar> = (z: Vec) => (k: Scalar): Vec => [ z[0] * k, z[1] * k ]; const compose = (z: Vec) => (...actions: Array<(z: Vec) => Vec>) => actions.reduce((z, g) => g(z), z);

Dolor 1

Es muy extraño que en JavaScript no haya sobrecarga del operador. Parece que con un uso tan extendido de gráficos vectoriales y de trama, es mucho más conveniente trabajar con vectores o números complejos en una forma "clásica". Los conceptos de acción reemplazarían las operaciones aritméticas. Entonces, por ejemplo, rotación alrededor de algún vector $a$ en la esquina $\ phi$ se expresaría de manera trivial:

T_{- a} c i r c R_{p h i} c i r c T_{a} L e f t r i g h t a r r o w z r i g h t a r r o w (z - a) e^{i p h i} + a

$T _ {- a} \ circ R _ {\ phi} \ circ T_ {a} \ Leftrightarrow z \ rightarrow (z-a) e ^ {i \ phi} + a$

Desafortunadamente, JS no sigue el desarrollo de la maravillosa idea de Pitágoras "El mundo es un número", a diferencia, al menos, de Python.

Tenga en cuenta que hasta ahora hemos estado trabajando con un grupo de transformaciones continuas. Sin embargo, la computadora no funciona con cantidades continuas, por lo tanto, siguiendo a Poincare, entenderemos un grupo continuo como un grupo infinito de operaciones discretas. Ahora que hemos descubierto la geometría, deberíamos recurrir a la relatividad del movimiento.

Cosmología del lienzo. Rejilla modular

Durante un siglo, como humanidad, la expansión del universo ha sido conocida. Observando objetos distantes, galaxias y cuásares, registramos el desplazamiento del espectro electromagnético hacia ondas más largas, el denominado desplazamiento al rojo cosmológico. Cualquier medición conecta al observador, lo observado y los medios de medición en relación con los cuales hacemos nuestras mediciones. Sin instrumentos de medición, es imposible establecer relaciones invariables en la naturaleza, es decir, determinar la geometría del Universo. Sin embargo, la geometría pierde su significado sin observabilidad. Entonces, en nuestra tarea, es bueno tener puntos de referencia, como galaxias, en relación con la luz de los cuales podemos determinar la relatividad del movimiento de nuestro lienzo. Dicha estructura puede ser una red periódica, que se bifurca cada vez que el espacio se expande dos veces.

Como la red es periódica, es conveniente adoptar un álgebra modular. Por lo tanto, actuaremos como un grupo $P$ también en el toro $T ^ 2 = S ^ 1 \ veces S ^ 1$ . Dado que la pantalla del monitor no es un plano continuo, sino una red entera $\ mathbb {Z} ^ 2$ (descuidamos ahora que es finito), entonces la acción del grupo $P$ debe considerarse en un toro entero $\ mathbb {Z} _ {p} ^ 2$ donde $p$ - el tamaño del borde del cuadrado $p \ veces p$ :

Por lo tanto, de una vez por todas arreglando nuestro toro cerca del origen, realizaremos todos los cálculos adicionales sobre él. Luego propagarlo utilizando métodos de biblioteca de lienzo estándar. Así es como se ve un movimiento de un píxel:

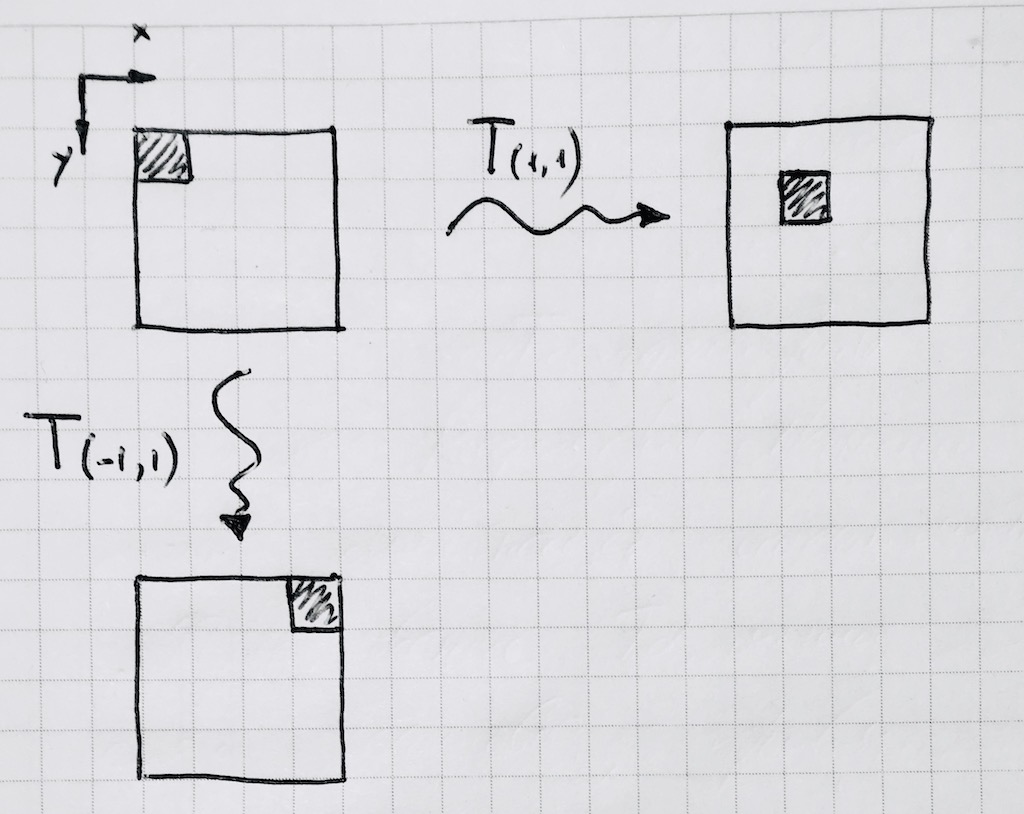
Obviamente, la operación estándar de tomar el módulo x% p no es adecuada para nosotros, ya que traduce los valores negativos del argumento en negativos, pero no hay ninguno en el toro de enteros. Escribe tu función $x \ mod p$ :

 const mod = (x, p) => x >= 0 ? Math.round(x) % p : p + Math.round(x) % p;

Ahora volvamos a la máquina de estado final y

definirlo

La clase FSM se hereda convenientemente de EventEmitter, que nos proporcionará la capacidad de suscribirnos.

 class FSM<States> extends EventEmitter { static get TRANSITION() { return '__transition__'; } state: States; scheme: Scheme<States>; constructor(state: States, scheme: Scheme<States>) { super(); this.state = state; this.scheme = scheme; this.on(FSM.TRANSITION, event => this.emit(this.state, event)); } get isActive(): boolean { return typeof(this.scheme[this.state]) === 'object'; } dispatch(event: Event) { if (this.isActive) { const transition = this.scheme[this.state].find(({ where }) => where(event).every(domen => domen) ); if (transition) { this.state = transition.to; this.emit(FSM.TRANSITION, event); } } } }

A continuación, defina un esquema de transición, cree un lienzo y

Inicializar todo.

 canvas = document.getElementById('canvas'); ctx = canvas.getContext('2d'); // Create a pattern, offscreen patternCanvas = document.createElement('canvas'); patternContext = patternCanvas.getContext('2d'); type States = | 'idle' | 'pressed' | 'dragging' | 'zooming'; const scheme: Scheme<States> = { 'idle': [ { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'zooming', where: event => [event.type === 'wheel'] }, ], 'pressed': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'moving': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'zooming': [ { to: 'zooming', where: event => [event.type === 'wheel'] }, { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'idle', where: event => [true] }, ], }; const fsm: FSM<States> = new FSM('idle', scheme); const dispatch = fsm.dispatch.bind(fsm);

Luego debe determinar la función de representación, establecer los valores iniciales necesarios y suscribirse al cambio de estado. Considere la parte más interesante del código:

  fsm.on('zooming', (event: WheelEvent) => { // next scale factor const nk = g >= 1 ? round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e2) : round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e12); // gain g = 2 ** Math.trunc(Math.log2(nk)); if (g < min || g > max) return; vec = compose(vec)( T([-event.clientX, -event.clientY]), S(nk / k), T([event.clientX, event.clientY]) ); size = base * nk; patternCanvas.width = Math.round(size / g); patternCanvas.height = Math.round(size / g); xyMod = [ mod(vec[0], patternCanvas.width), mod(vec[1], patternCanvas.height) ]; k = nk; main(); });

Primero, no nos expandimos por el coeficiente k, sino por alguna relación nk / k. Esto se debe al hecho de que el paso m de nuestro mapeo en un punto fijo $(a, b)$ expresado como

x_{m} = (x_{m - 1} - a) k_{m - 1}^{*} + a y_{m} = (y_{m - 1} - b) k_{m - 1}^{*} + b

$x_ {m} = (x_ {m-1} -a) k_ {m-1} ^ * + a \\ y_ {m} = (y_ {m-1} -b) k_ {m-1} ^ * + b$

o, relativo a los valores iniciales $x_ {1}, y_ {1}$

x_{m} = (x_{1} - a) p r o d_{i = 1}^{m - 1} k_{i}^{*} + a y_{m} = (y_{1} - b) p r o d_{i = 1}^{m - 1} k_{i}^{*} + b

$x_ {m} = (x_ {1} -a) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + a \\ y_ {m} = (y_ {1} -b) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + b$

Obviamente el producto $\ prod_ {i = 1} ^ {m-1} k_ {i} ^ *$ Hay una función no lineal del paso de iteración y converge muy rápidamente a cero o se escapa al infinito con pequeñas desviaciones iniciales.

Introducimos la variable g, que es una medida de duplicar nuestro lienzo. Obviamente, adquiere un valor constante en un cierto intervalo. Para lograr linealidad $k_ {i} ^ *$ usamos sustitución homogénea

k_{i + 1}^{*} = f r a c k_{i + 1} k_{i}, k_{1} = 1

$k_ {i + 1} ^ * = \ frac {k_ {i + 1}} {k_ {i}}, k_ {1} = 1$

Entonces todos los miembros en el trabajo, excepto el primero y el último, se reducirán:

p r o d_{i = 1}^{m - 1} k_{i}^{*} = p r o d_{i = 1}^{m - 1} f r a c k_{i} k_{i - 1} = f r a c k_{2} 1 f r a c k_{3} k_{2} . . . f r a c k_{m - 2} k_{m - 3} f r a c k_{m - 1} k_{m - 2} = k_{m - 1}

$\ prod_ {i = 1} ^ {m-1} k_ {i} ^ * = \ prod_ {i = 1} ^ {m-1} \ frac {k_ {i}} {k_ {i-1}} = \ frac {k_ {2}} {1} \ frac {k_ {3}} {k_ {2}} ... \ frac {k_ {m-2}} {k_ {m-3}} \ frac { k_ {m-1}} {k_ {m-2}} = k_ {m-1}$

Además, el salto de fase g reduce la velocidad de expansión de tal manera que la estructura fractal que se desarrolla ante nosotros siempre se mueve linealmente. Por lo tanto, obtenemos una variación aproximada de la ley de poder de Hubble de la expansión del Universo.

Queda por comprender los límites de precisión de nuestro modelo.

Fluctuaciones cuánticas. Campo de número 2-adic

La comprensión del proceso de medición condujo al concepto de un número real. El principio de incertidumbre de Heisenberg apunta a sus límites. Una computadora moderna no funciona con números reales, sino con palabras de máquina, cuya longitud está determinada por la capacidad del procesador. Las palabras de máquina forman un campo de números 2-adic $\ mathbb {Q_ {2}}$ y se denotan como $\ mathbb {F_ {2} ^ {n}}$ donde $n$ - longitud de palabra. El proceso de medición en este caso es reemplazado por el proceso de cálculo y está asociado con una métrica no Archimedean:

f o r a l l n i n m a t h b b Z, z i n m a t h b b F_{2}^{n} : n c d o t z < 2^{n}

$\ forall n \ in \ mathbb {Z}, z \ in \ mathbb {F_ {2} ^ {n}}: n \ cdot z <2 ^ n$

Por lo tanto, nuestro modelo tiene un límite de cálculo. Las limitaciones se describen en el estándar IEEE_754 . Comenzando en algún momento, nuestro tamaño base irá más allá del límite de precisión y la operación de tomar el módulo comenzará a generar errores que se asemejan a secuencias pseudoaleatorias. Esto se verifica simplemente eliminando la línea

 if (g < min || g > max) return;

El límite final en nuestro caso se calcula mediante el método semiempírico, ya que trabajamos con varios parámetros.

Conclusión

Por lo tanto, aparentemente distantes a primera vista, las teorías están conectadas en el lienzo en el navegador. Los conceptos de acción, medición y cálculo están estrechamente relacionados entre sí. El problema de combinarlos aún no está resuelto.