Las discusiones sobre los pros y los contras del nuevo formato revolucionario de punto flotante Posit están en curso. El siguiente argumento en la discusión fue la
afirmación de que, de hecho, la tarea de Posit es almacenar datos de forma compacta y no ser utilizada en absoluto en los cálculos; mientras que los cálculos se realizan en aritmética Quire con mayor precisión, que también forma parte del estándar Posit.
Bueno, tienda, tienda. ¿Qué significa "almacenar" números después de los cálculos realizados con mayor precisión de lo que permite el formato de almacenamiento? Significa redondear, y redondear significa cometer errores. Los errores se pueden estimar de diferentes maneras, y para que no se repitan, hoy utilizamos el análisis espectral utilizando la transformada de Fourier.
Muy breve introducción
Si tomamos una señal en forma de sinusoide y realizamos una transformada de Fourier en ella, entonces en el espectro deberíamos obtener un solo pico; de hecho, el espectro puede contener armónicos con una frecuencia que es un múltiplo del tono fundamental obtenido como resultado de una distorsión no lineal, y una plataforma de ruido obtenida como resultado de ruido, interferencia y digitalización. Aquí mediremos el nivel de estos ruidos.
Inicio
Para hacerlo aún más interesante, como señal de prueba, no tomamos una sinusoide, sino varias; Es necesario asegurarse de que los períodos de estas sinusoides se ajusten perfectamente al período de la transformada discreta de Fourier. En Wolfram Mathematica, esto se puede hacer, por ejemplo, así:
sz = 8192; data = Table[2 Sum[ Sin[Prime[j] k 2 Pi/sz + j*j]/sz, {j, 100, 200, 2}] // N, {k, 0, sz - 1}];
Los números primos se usan aquí para la aniquilación desigual de frecuencias; y j * j desplaza la fase de la sinusoide dependiendo de la frecuencia para evitar picos fuertes en la señal de prueba, proporcionándole una amplitud más o menos uniforme. La señal recibida visualmente se ve así:
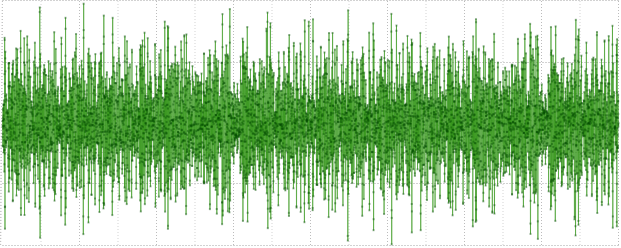
Luego, lo normalizamos a la unidad por el valor máximo, luego lo convertimos a un entero de 32 bits Int, Float, Posit y nuevamente a Double. Si las afirmaciones de los autores son correctas, entonces el error introducido por la transformación Doble → Posit → Doble estará más cerca de Doublé que de Flotar.
Analizaremos el nivel de ruido en unidades estándar para el procesamiento de señales: decibelios, que nos permiten comparar valores en una escala logarítmica. Como herramienta, utilicé mi propio analizador de espectro, una vez escrito para fines de investigación.
Entonces
azul - flotador
rojo - Posit
púrpura - Int32
azul - doble
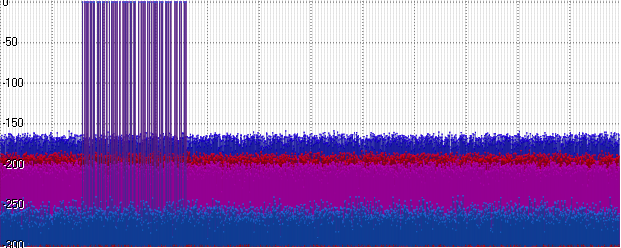
Posit, por supuesto, resultó ser un poco mejor que Float, pero todavía está lejos del nivel Doble. Y al mismo tiempo, ¡peor que Int32! Es lógico, porque parte de los bits toma un orden de magnitud ... Usemos este orden: aumente la amplitud de nuestra señal a 1000:
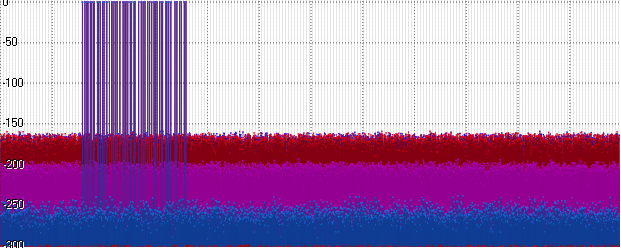
De repente (y de hecho bastante esperado), el ruido en Float y Posit se puso al día. Adelante: aumente la amplitud a mil millones:
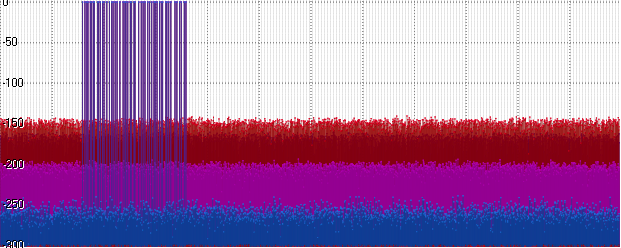
El flotador muestra el mismo nivel y Posit comienza a retrasarse. Un aumento adicional en la amplitud (aquí 10
15 ) conduce a un aumento adicional en la plataforma de ruido:
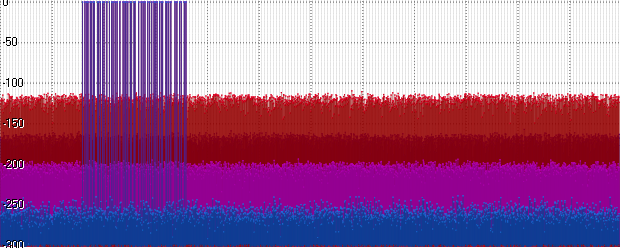
Conclusión
El milagro aún no sucedió. El análisis espectral no confirmó las afirmaciones de los autores de que el uso del formato Posit como almacenamiento puede proporcionar una precisión cercana a Double. Incluso en las mejores condiciones, el nivel de ruido en Posit fue solo 20 decibelios más bajo que Flotante, pero al mismo tiempo más alto que Int32 por 10 decibelios, y más alto que Doble por 60 decibelios.
Por supuesto, Posit puede encontrar una aplicación útil, como protección contra ir más allá del rango permitido, cuando las emisiones que exceden significativamente los valores normales no conducirán a un recorte o desbordamiento. Pero incluso en este escenario, Posit actúa más como un compromiso entre Int y Float, en lugar de un formato de número claramente mejor.