¿Existe un objetivo, una oportunidad ideal, o es el resultado de nuestra ignorancia?
La vida es impredecible y los accidentes nos suceden todo el tiempo. Podemos decir que el universo mismo es accidental. Y, sin embargo, de alguna manera, un gran número de eventos aleatorios puede crear patrones a gran escala que la ciencia puede predecir. La disipación de calor y el movimiento browniano son solo dos ejemplos de tales eventos.
Recientemente, un accidente incluso llegó a las noticias: resultó que las superficies aleatorias
tienen un orden oculto , y también podríamos haber estado cerca de ver cómo una computadora cuántica
genera una aleatoriedad perfecta . El último caso, la búsqueda de una aleatoriedad perfecta, es importante porque la aleatoriedad trae imprevisibilidad, y todos los intentos de tecnología no cuántica para lograrlo tienen un defecto oculto: se implementan utilizando algoritmos que, en teoría, se pueden descifrar. En esta columna, aprenderemos cómo crear aleatoriedad y vencerla en la vida cotidiana, antes de subir a las alturas filosóficas del debate sobre lo que es la verdadera aleatoriedad.
Riddle 1: combinaciones aleatorias
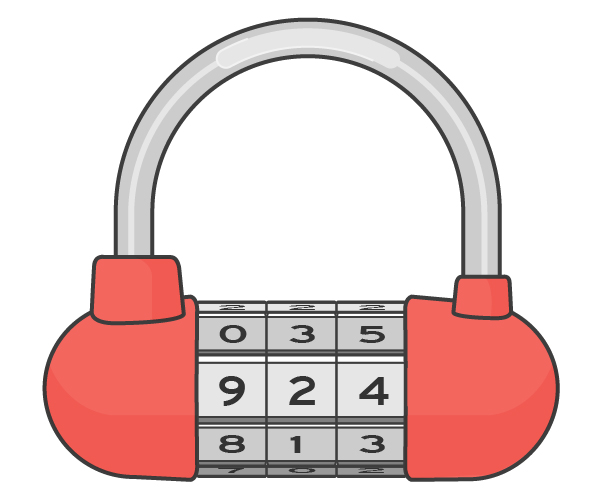
Considere un código de bloqueo simple para una bicicleta, similar a la imagen a continuación. Tiene tres discos giratorios, cada uno de los cuales muestra 10 dígitos en orden. Cuando estos tres discos se giran para obtener la combinación deseada, 924, se abre el bloqueo. Cuando desee cerrarlo, debe mezclar los números para que estén muy lejos de la combinación dada. Pero, ¿qué significa "lejos" en este contexto? Si mueve el disco lo máximo posible en 5 posiciones, establecerá el número 479. Sin embargo, será fácil para un atacante tropezar accidentalmente con esta posición si simplemente gira los cinco discos al mismo tiempo y ve si se abre el bloqueo. Imagine que una galleta tiene tiempo para probar cinco combinaciones diferentes. En cada caso, nuestro ladrón potencial prueba nuestro castillo después de una de las siguientes acciones (y en caso de falla, devuelve el castillo a su configuración original):
- Gire una unidad en un número aleatorio de posiciones.
- Gire dos discos simultáneamente en un número aleatorio de posiciones.
- Gire los tres discos al mismo tiempo por un número aleatorio de posiciones.
- Gire dos discos en diferentes ángulos.
- Gire los tres discos de manera diferente.
Nuestro enigma es el siguiente: si el código de desbloqueo de la cerradura es 924, ¿qué conjunto de números mixtos será el más estable para los intentos aleatorios de abrir la cerradura, y cuántos conjuntos existen? ¿Cuál es la probabilidad de detectar código?
Enigma 2: de la aleatoriedad al orden en acertijos
A menudo me sorprende cuán similar es el proceso de resolver el rompecabezas al progreso científico. Pasamos de la aleatoriedad al orden, agregando piezas, y nuestra confianza en la corrección de la solución se alimenta con cada nueva pieza adecuada. En la segunda tarea, intentaremos crear una forma de medir nuestro progreso en el camino desde un estado desordenado aleatorio hasta una solución completa y ordenada.
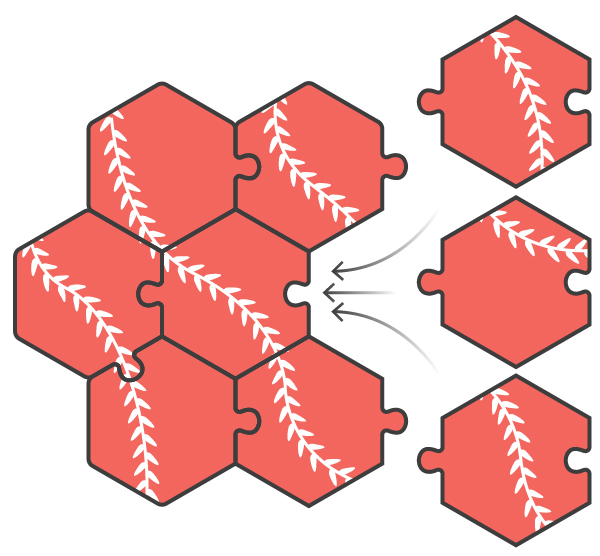
Supongamos que resolvemos un rompecabezas que consta de piezas hexagonales, como panales. La imagen del rompecabezas es una vid sinuosa. Dado que el patrón se repite y es similar, no se puede garantizar que dos piezas adyacentes encajen físicamente entre sí, incluso si encajan en la imagen. Suponga que otros tres pueden ir a cada borde de una pieza dada. Por lo tanto, cuando dos piezas encajan entre sí en la imagen, la probabilidad de que encajen físicamente será del 33,33%. Sin embargo, si puede encontrar otra pieza que se ajuste a ambos, es decir, una que tenga una ventaja común con cada uno de estos dos, entonces aumentará su confianza en el éxito. Intentemos evaluar cuánto crece.
- Usted ha encontrado tres piezas que parecen encajar a primera vista, sin el desplazamiento obvio del patrón de lianas en sus bordes adyacentes. ¿Cuál es la medida de su confianza en la selección correcta de piezas?
- Has encontrado una pieza hexagonal central y seis que la rodean, y en la imagen parecen coincidir. ¿Cuál es la medida de su confianza en la selección correcta de piezas?
Cuanto más grandes sean los grupos de piezas, mayor será su confianza en el ensamblaje correcto. Es razonable suponer que tres grupos aislados, en los que hay un total de siete piezas conectadas, no son comparables con el único hexágono rodeado descrito anteriormente.
La tercera parte de este acertijo tiene correcciones, y es un intento de cuantificar la diferencia anterior. ¿Es posible llegar a una medida del grado de finalización de un rompecabezas parcialmente resuelto? Este método debería permitirle asignar un número de 0 a 100 a cualquier rompecabezas parcialmente ensamblado de 10x10 hexágonos. Este número debe indicar el grado de finalización, correlacionando aproximadamente con la proporción del estado actual del rompecabezas en relación con la versión terminada.
Riddle 3: ¿es posible una coincidencia perfecta?
Para esta parte, le daré una variante del famoso debate de Einstein-Bohr sobre el azar. Los participantes del debate pueden unirse a los equipos E o B.
Ambos equipos están de acuerdo en que, en el macrocosmos, la existencia de mecanismos de generación aleatoria solo es posible porque no entendemos las fuerzas o los algoritmos subyacentes. Si conociera todas las fuerzas que actúan sobre una moneda lanzada o un dado, si tuviera suficiente poder de cómputo, podría predecir el resultado. Según la prevalencia de las opiniones del equipo B, se nos enseña que esto no es así en el mundo cuántico: las probabilidades cuánticas deben ser objetivas. ¿Pero es esto posible? ¿Podría haber algún mecanismo en el mundo subcuántico de Planck que decida cuál de las dos opciones igualmente probables se implementará, incluso si nunca tendremos la oportunidad de estudiar este nivel? Incluso si la pesadilla de Einstein con un dado que juega a los dados es real, esta deidad debería tener algún tipo de algoritmo en su cabeza que decida cada elección, sin importar cuán extraña e ilógica sea. Entonces la oportunidad se deberá nuevamente a nuestra ignorancia. Será desconocido solo en la práctica, y no aleatoriamente objetivo.
La respuesta estándar del Equipo B es que el mundo cuántico es simplemente demasiado extraño para aplicarle las reglas que hemos aprendido de nuestra experiencia en la interacción con el macrocosmos. Sin embargo, hay dos tipos de rarezas. Por un lado, la extrañeza puede estar en la imposibilidad física de moverse más rápido que la velocidad de la luz. Tal extrañeza puede existir, y solo significará que necesitamos reconsiderar nuestra comprensión de la ley física en circunstancias especiales, tal como Einstein revisó la ley de adición de las velocidades de Newton, que se vuelve falsa a valores muy grandes.
Por otro lado, algo puede ser extraño en términos de imposibilidad lógica, como 2 + 2 es igual a 5. Tal resultado es imposible en cualquier universo. El equipo E puede argumentar que la posibilidad perfecta y las probabilidades objetivas son lógicamente imposibles. No debemos aceptarlos, sino que debemos encontrar mecanismos físicos que puedan explicar los resultados observados, independientemente de las leyes físicas existentes que puedan violar.
¿A qué equipo te unes?
PD: Las respuestas se publicarán más tarde.