Hola
En este "artículo", o más bien en el ensayo, mostraré una forma muy simple de divertirme conociendo los conceptos básicos del látex y la pitón.
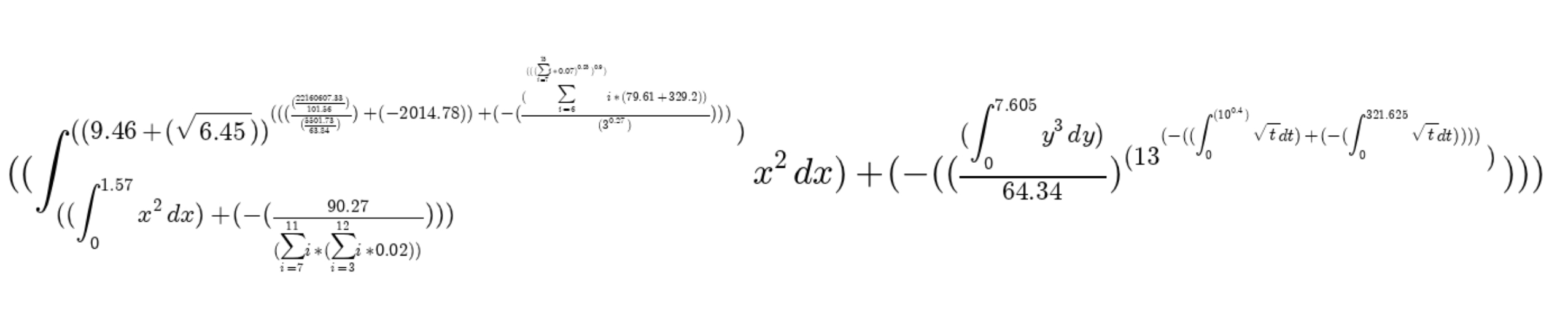
Por qué
Bueno, puedes generar expresiones simples para que los niños cuenten. O simplemente así. Sí, al menos ponte el fondo de pantalla, si eres tan fanático como yo.
¿Cómo se supone que esto funciona?
La idea es realmente muy simple, absolutamente cualquiera puede escribir un programa así. Queremos generar una expresión igual a algún número n (que el usuario ingresa). Cualquier número puede reemplazarse con una expresión aritmética, por ejemplo, 3 = 1 + 2. Y 2 es 4/2. Así es como generamos 3 = 1 + 4/2. Del mismo modo, presentamos varias operaciones diferentes y lo envolvemos en LaTeX, el lenguaje de fórmulas.
Necesitarás ...Experiencia de una semana en python y matplotlib. Lo digo en serio
Mecanismo principal
Necesitamos analizar la expresión para sacar los números de allí. Llamemos a nuestra clase como generadora de problemas (¡todos la extrañamos mucho!)
import random from math import log import math import sys sys.setrecursionlimit(1000)
El significado de la función extract_nums es obtener n pares de números (a, b), donde a es la posición del primer carácter, b es la posición del último + 1.
Por ejemplo, si ejecutamos el siguiente código:
gen = ProblemGenerator() print(gen.extract_nums("13+256/355+25"))
Veremos:
[(0, 2), (3, 6), (7, 10), (11, 13)]
Es decir, es una matriz de tuplas. (0, 2) significa que hay un número entre 0 (inclusive) y 2 (no incluido).
Ahora nos gustaría hacer diferentes operadores, comencemos con la multiplicación y la suma. Declara tres funciones
def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b) return a + " * " + b
La esencia de la función unmin es no solo convertir todos los argumentos en cadenas, sino también poner entre paréntesis algún operando si es menor que cero. Por ejemplo, obtuvimos los números a = 3, b = -4. Si escribimos
a = 3 b = -4 a, b = unmin(a, b)
Entonces a = "3", b = "(- 4)"
Bueno, el resto de las funciones son claras: __c_sum devuelve una cadena de la forma "13 + 4" y __c_mul "13 * 4".
Queda combinar estas dos piezas y reemplazar cada número en la expresión con la expresión.
Agregue el siguiente código a ProblemGenerator:
class ProblemGenerator: ... def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e
complexify toma algún número y devuelve una cadena, una expresión complicada. Por ejemplo, si escribimos:
gen = ProblemGenerator() gen.add_expander(__c_sum) print(gen.complexify(13))
Obtenemos:
31.2 + (-18.2)
¿Cómo funciona __rxp__? Seleccionamos al azar la posición de un número de una expresión (por ejemplo, si hay una expresión "13 + 35/45", entonces digamos que seleccionamos (3, 5)) y reemplazamos este número con una expresión igual a ese número. Es decir, me gustaría:
"13 + 35/45" - un número aleatorio (3, 5)
"13+" + "(12 + 23)" + "/ 45"
"13+ (12 + 23) / 45"
Así es como funciona __rxp__
Bueno, randexpr funciona de manera bastante simple. Por ejemplo, si tenemos cuatro pasos, la expresión se abrirá así:
13 (5.62 + 7.38) ((20.63 + (-15.01)) + 7.38) ((20.63 + (-(67.5 + (-52.49)))) + 7.38) ((20.63 + (-((15.16 + 52.34) + (-52.49)))) + 7.38)
Intentemos ejecutar:
gen = ProblemGenerator() gen.add_expander(__c_sum) gen.add_expander(__c_mul) exp = gen.randexpr(1, 5) print(exp)
Resultado:
((6.63 + (56.62 + 16.8)) + (-((60.53 + 3.61) + 14.91)))
LaTeX
Curiosamente, los restos más simples. Anunciaremos varios operadores diferentes de LaTeX:
def __l_sum(num): a = 100 ** (random.random() * 2) b = num - a a, b = unmin(a, b) return a + " + " + b def __l_div(num): a = num * (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = a / num a, b = unmin(a, b) return "\\frac{" + a + "}{" + b + "}" def __l_pow(num): if num == 0: return str(random.randint(2, 7)) + "^{-\\infty}" a = random.randint(0, 10) + 3 b = math.log(abs(num), a) a, b = unmin(a, b) return ("-" if num < 0 else "") + a + "^{" + b + "}" def __l_sqrt(num): a = num ** 0.5 a = unmin(a)[0] return "\\sqrt{" + a + "}" def __l_int(num): patterns = [ ("x^{2}", (3 * num) ** (1/3), "dx"), ("y^{3}", (4 * num) ** (1/4), "dy"), ("\sqrt{t}", (1.5 * num) ** (2/3), "dt") ] p, b, f = random.choice(patterns) b = str(round(b, 3)) return "\\int_{0}^{" + b + "} " + p + " " + f def __l_sig(num): a = random.randint(1, 10) b = random.randint(1, 10) + a s = sum([i for i in range(a, b + 1)]) c = num / s a, b, c = unmin(a, b, c) return "\\sum_{i=" + a + "}^{" + b + "} i*" + c
Agregue todas las funciones a gen:
gen = ProblemGenerator() gen.add_expander(__l_sum)
Finalmente, agregue la salida del resultado:
import matplotlib.pyplot as plt plt.axis("off") latex_expression = gen.randexpr(1, 30)
Eso es todo
Código completo import random from math import log import math import sys sys.setrecursionlimit(1000) class ProblemGenerator: def extract_nums(self, exp): symbols = list(exp) NUM = "1234567890." for i in range(len(symbols)): symbols[i] = "N" if symbols[i] in NUM else "T" begins = [] ends = [] for i in range(len(symbols) - 1): fn = symbols[i] + symbols[i + 1] if fn == "TN": begins.append(i) elif fn == "NT": ends.append(i) if exp[-1] in NUM: ends.append(len(exp) - 1) if exp[0] in NUM: begins = [-1] + begins return [(x + 1, y + 1) for x, y in zip(begins, ends)] def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b, acc=5) return a + " * " + b def __c_sub(num): a = num + 100 ** (random.random() * 2) b = (a - num) a, b = unmin(a, b) return a + " - " + b def __c_log(num): fr = random.randint(300, 500) a = math.e ** (num / fr) a, fr = unmin(a, fr, acc=5) return "log(" + a + ") * " + fr def __l_sum(num): a = 100 ** (random.random() * 2) b = num - a a, b = unmin(a, b) return a + " + " + b def __l_div(num): a = num * (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = a / num a, b = unmin(a, b) return "\\frac{" + a + "}{" + b + "}" def __l_pow(num): if num == 0: return str(random.randint(2, 7)) + "^{-\\infty}" a = random.randint(0, 10) + 3 b = math.log(abs(num), a) a, b = unmin(a, b) return ("-" if num < 0 else "") + a + "^{" + b + "}" def __l_sqrt(num): a = num ** 0.5 a = unmin(a)[0] return "\\sqrt{" + a + "}" def __l_int(num): patterns = [ ("x^{2}", (3 * num) ** (1/3), "dx"), ("y^{3}", (4 * num) ** (1/4), "dy"), ("\sqrt{t}", (1.5 * num) ** (2/3), "dt") ] p, b, f = random.choice(patterns) b = str(round(b, 3)) return "\\int_{0}^{" + b + "} " + p + " " + f def __l_sig(num): a = random.randint(1, 10) b = random.randint(1, 10) + a s = sum([i for i in range(a, b + 1)]) c = num / s a, b, c = unmin(a, b, c) return "\\sum_{i=" + a + "}^{" + b + "} i*" + c gen = ProblemGenerator() gen.add_expander(__l_sum) gen.add_expander(__l_div) gen.add_expander(__l_pow) gen.add_expander(__l_sqrt) gen.add_expander(__l_int) gen.add_expander(__l_sig) import matplotlib.pyplot as plt plt.axis("off") latex_expression = gen.randexpr(1, 30)
Resultado (3 capturas de pantalla)