Dos páginas fueron suficientes para probar la hipótesis de 30 años del campo de la informática.

La hipótesis de la "sensibilidad" desconcertó a muchos científicos informáticos prominentes, pero su nueva evidencia resultó ser tan simple que un investigador podría reducirla a un solo tweet

El trabajo publicado este verano pone fin a los casi 30 años de historia de la hipótesis con respecto a la estructura de los bloques de construcción fundamentales de los circuitos informáticos. Esta hipótesis de "sensibilidad" ha dejado perplejos a muchos científicos informáticos prominentes durante años, pero su nueva evidencia resultó ser tan simple que un investigador podría reducirla a un solo tweet.

"Esta hipótesis fue una de las tareas abiertas más molestas y vergonzosas en toda la combinatoria e informática teórica", escribió Scott Aaronson, de la Universidad de Texas en Austin, en su blog. "La lista de personas que intentaron probarlo y no lo hicieron es una lista de las personas más prominentes en matemáticas discretas y ciencias de la computación teóricas", agregó en un correo electrónico.

Esta hipótesis está asociada con las funciones booleanas: las reglas para convertir cadenas de bits entrantes (ceros y unos) en un solo bit. Una de esas reglas produce 1 cuando todos los bits entrantes son 1 y 0 en caso contrario; otra regla devuelve 0 si la línea contiene un número par de unidades y 1 en otro caso. Cada circuito de computadora es una combinación de funciones booleanas, lo que los convierte en "el material de construcción de todo lo que se hace en informática", dijo Rocco Cenedio, de la Universidad de Columbia.


Con los años, se han desarrollado muchas formas en informática para medir la complejidad de una función booleana dada. Cada medida utiliza su propio aspecto de cómo la información de la línea de entrada determina el bit de salida. Por ejemplo, la "sensibilidad" de una función booleana, más o menos, indica la probabilidad de que el cambio de un solo bit en la entrada cambie el bit en la salida. Y la "complejidad de la solicitud" calcula cuántos bits entrantes deben solicitarse para saber con certeza cuál será el saliente.

Cada medida ofrece su propio punto de vista único sobre la estructura de una función booleana. Sin embargo, los científicos informáticos descubrieron que casi todas estas medidas se ajustan a una plataforma universal y que, por el valor de una de ellas, se puede juzgar aproximadamente la importancia de las otras. Y solo una medida de complejidad no encajaba en este esquema: la sensibilidad.

En 1992, Noam Nisan de la Universidad Hebrea de Jerusalén y Mario Szeged, que ahora trabajan en la Universidad de Rutgers, sugirieron que la sensibilidad aún encaja en esta plataforma. Pero nadie pudo probarlo. "Esta pregunta, diría, fue sobresaliente en el campo del estudio de las funciones booleanas", dijo Cenedio.

"La gente escribió trabajos largos y complejos, tratando de hacer muy poco progreso", dijo Ryan O'Donnell, de la Universidad Carnegie Mellon.

Y ahora, Hao Huang , matemático de la Universidad de Emory, ha demostrado la hipótesis de sensibilidad con la ayuda de una brillante pero elemental prueba de dos páginas relacionada con la combinación de puntos en cubos. "Es hermoso, como una perla preciosa", escribió Claire Matthew, del Centro Estatal de Investigación Científica de Francia en una entrevista en Skype.

Aaronson y O'Donnell llamaron a la obra de Juan "libro" prueba de la hipótesis de la sensibilidad, refiriéndose al concepto del "libro celestial" de Pal Erdös, en el que Dios escribe las pruebas ideales de cada teorema. "Es difícil para mí imaginar que incluso Dios conoce una prueba más simple del teorema de la sensibilidad", escribió Aaronson.

Tema sensible

Imagine, dijo Matthew, que está completando un formulario con preguntas en el formulario de solicitud de préstamo bancario, cuyas respuestas pueden ser sí / no. Cuando haya terminado, el banquero evaluará los resultados y le dirá si es apto para un préstamo. Este proceso es una función booleana: sus respuestas son bits entrantes y la decisión del banquero es saliente.

Si su solicitud es denegada, puede pensar si podría cambiar el resultado al formular una sola pregunta, tal vez al afirmar que gana más de $ 50,000 al año, aunque esto no es así. Si esta mentira cambia el resultado de la consideración, los informáticos llamarán a esa función booleana "sensible" al valor de un bit en particular. Si, por ejemplo, puede acostarse en uno de los siete lugares, y cada vez cambiar el resultado, la sensibilidad de la función booleana de evaluar su solicitud de préstamo es siete.

Los informáticos definen la sensibilidad general de una función booleana como el valor de sensibilidad más alto para todas las opciones posibles para completar una solicitud. En cierto sentido, esta medida calcula cuántos problemas serán realmente importantes en la mayoría de los casos límite, en aplicaciones, cuyo resultado se cambia más fácilmente si las aplicaciones mismas se modifican ligeramente.


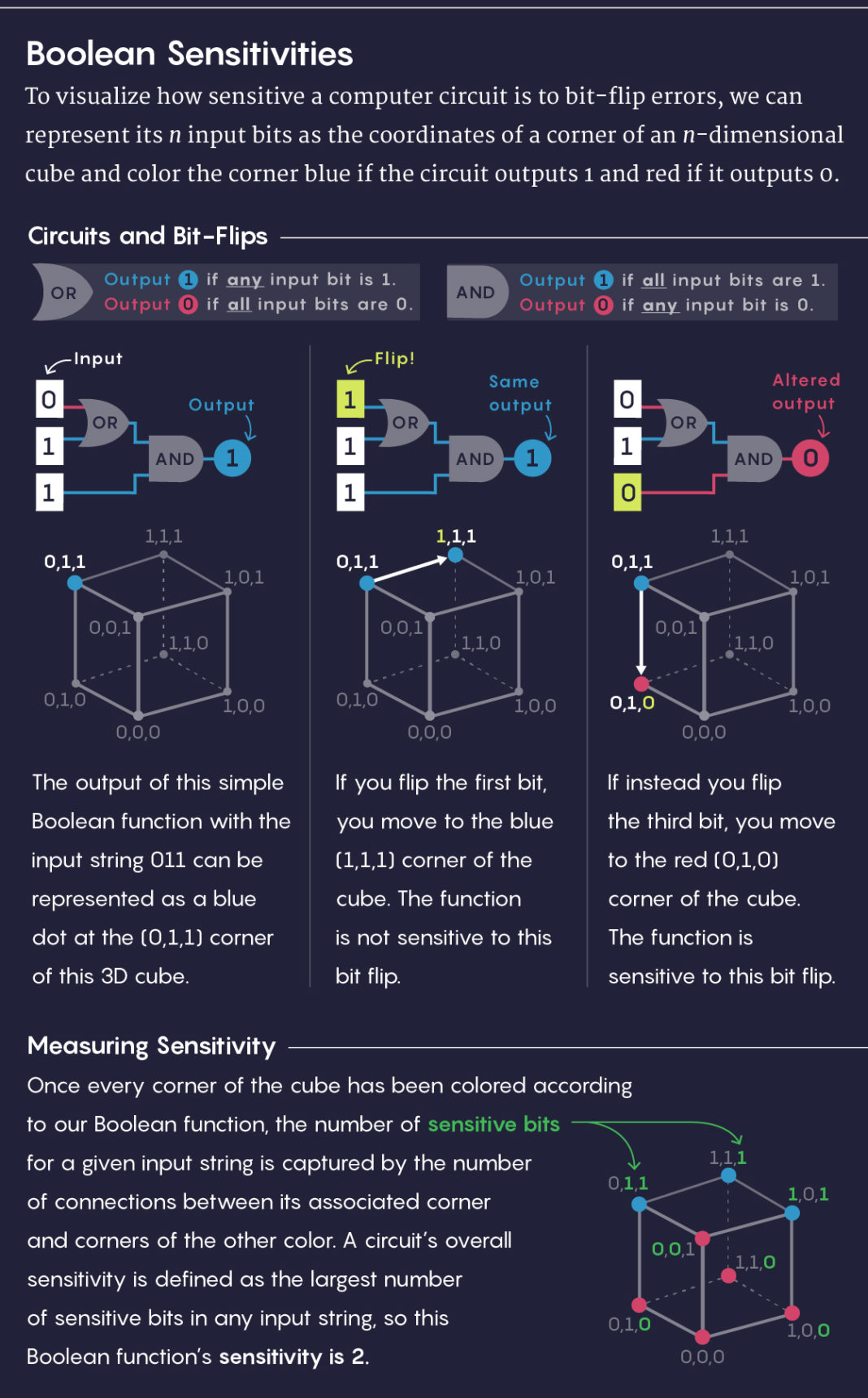Para visualizar la sensibilidad del circuito a los errores con la inversión de bits, n bits entrantes se pueden representar como las coordenadas de los vértices de un cubo n-dimensional. Colorearemos el vértice de azul si la ruta produce 1, y de rojo si 0.

En el centro a la izquierda: la salida de una función booleana simple con la entrada 011 se puede representar con un punto azul en la parte superior del cubo (0,1,1).
Centro: girando el primer bit, iremos a la parte superior azul del cubo (1,1,1). La función no es sensible a la inversión de este bit.
En el centro a la derecha: girando el tercer bit, iremos a la parte superior roja del cubo (0,1,0). La función es sensible a la inversión de este bit.

Habiendo coloreado todos los vértices del cubo, obtenemos el número de bits sensibles para una línea entrante dada igual al número de conexiones entre el vértice correspondiente y los vértices de un color diferente. La sensibilidad del bucle se define como el mayor número de bits sensibles en cualquier línea de entrada, por lo que esta función tiene una sensibilidad de 2.

La sensibilidad suele ser una de las medidas más fáciles para calcular la complejidad, pero no es en absoluto una medida explicativa simple. Por ejemplo, nuestro banquero, en lugar de darle un formulario para completar, podría comenzar con una sola pregunta y luego usar su respuesta para determinar qué pregunta hacer a continuación. La mayor cantidad de preguntas que un banquero deberá hacer antes de tomar una decisión es la complejidad de solicitar una función booleana.

Tal medida aparece en una variedad de situaciones: por ejemplo, un médico puede querer enviar al paciente a recolectar la menor cantidad de pruebas posible para hacer un diagnóstico, o un experto en aprendizaje automático puede querer crear un algoritmo que estudie la menor cantidad posible de propiedades del objeto antes podrá clasificarlo correctamente. "En muchas situaciones, diagnóstico o capacitación, le gusta que la regla básica tenga poca complejidad de consulta", dijo O'Donnell.

Entre otras medidas está la búsqueda de la forma más simple de escribir una función booleana en forma de una expresión matemática, o calcular cuántas respuestas tendrá que mostrar el jefe al banquero para demostrar que la solicitud se ha procesado correctamente. Incluso hay una variante de la complejidad de la consulta de la física cuántica, cuando el banquero hace una "superposición" de varias preguntas a la vez. Al comprender cómo esta medida se relaciona con otras medidas de complejidad, los investigadores comprenden mejor las limitaciones de los algoritmos cuánticos.

Los informáticos han demostrado que existe una estrecha relación entre todas estas medidas, con la excepción de la sensibilidad. Más específicamente, descubrieron que están relacionados entre sí por dependencia polinómica; por ejemplo, una medida puede expresarse como un cuadrado o un cubo de otra. Y solo la sensibilidad se resistió obstinadamente, no queriendo integrarse en este conveniente esquema de clasificación. Muchos investigadores sospecharon que debería ser adecuado para él, pero no pudieron demostrar que no hay funciones booleanas extrañas cuya sensibilidad esté relacionada con otras medidas no por polinomio sino por dependencia exponencial, lo que en este caso significaría que la medida de sensibilidad es fundamentalmente más pequeño que el resto.

"Esta pregunta ha mantenido a la gente despierta durante 30 años", dijo Aaronson.

Rincón de la solución

Juan descubrió esta hipótesis a fines de 2012, en una cena con el matemático Michael Sachs del Instituto de Estudios Avanzados, donde Juan era un postdoctorado. Inmediatamente quedó fascinado por la simplicidad y elegancia de la hipótesis. "Y desde ese momento me obsesioné con los pensamientos sobre ella", dijo.

Juan agregó la hipótesis de la sensibilidad a la "lista secreta" de problemas que le interesaban, y cuando descubrió alguna nueva herramienta matemática, se preguntó si podría ayudarlo. "Cada vez después de la publicación de otro trabajo, volví a esta tarea", dijo. "Por supuesto, asigné tiempo y energía para trabajar en tareas más realistas".


Hao Huang en unas recientes vacaciones en Lisboa

Juan, como muchos en la comunidad de investigación, sabía que la hipótesis de sensibilidad se puede probar si los matemáticos pueden probar otra hipótesis con una condición más simple con respecto a un conjunto de puntos en cubos de diferentes dimensiones. Hay una forma natural de pasar de una cadena de ceros y unos a un punto en un cubo n-dimensional: simplemente use n bits como coordenadas de ese punto.

Por ejemplo, cuatro líneas de dos bits - 00, 01, 10 y 11 - corresponden a las cuatro esquinas de un cuadrado en un plano bidimensional: (0,0), (0,1), (1,0) y (1,1). Del mismo modo, ocho cadenas de tres bits corresponden a ocho esquinas de un cubo tridimensional, y así sucesivamente, para dimensiones más altas. La función booleana puede considerarse la regla de colorear estos ángulos de cubo con dos colores diferentes (por ejemplo, rojo para 0 y azul para 1).

En 1992, Craig Gotsman , que ahora trabaja en el Instituto de Tecnología de Nueva Jersey y Nati Lignal de la Universidad Hebrea, se dio cuenta de que la prueba de la hipótesis de sensibilidad se puede reducir a la respuesta a una simple pregunta sobre cubos de diferentes dimensiones: si toma cualquier conjunto que consista en más de la mitad de los vértices de los cubos , y colorearlos de rojo, es necesario encontrar un punto rojo conectado a muchos otros puntos rojos (por puntos "conectados" queremos decir que dos vértices están conectados por un borde común, y no se encuentran en diagonal).

Si nuestro subconjunto contiene exactamente la mitad de los vértices del cubo, es posible que no estén conectados entre sí. Por ejemplo, entre las ocho esquinas de un cubo tridimensional hay cuatro puntos,
(0,0,0), (1,1,0), (1,0,1) y (0,1,1) están ubicados diagonalmente el uno del otro. Pero en cuanto más de la mitad de los vértices de un cubo de cualquier dimensión se vuelven rojos, entre ellos los puntos rojos deben estar conectados entre sí. La pregunta es cómo se distribuyen estas conexiones. ¿Habrá al menos uno de estos picos con más conexiones?

En 2013, Juan comenzó a pensar que la mejor manera de comprender este problema probablemente sería utilizar el método estándar de representación de la red utilizando una matriz que realiza un seguimiento de los puntos que están conectados y luego estudia muchos números llamados valores propios de la matriz. Durante cinco años volvió periódicamente a esta idea, pero fue en vano. "Al menos por lo que pensaba de ella antes de acostarme, fue más fácil para mí dormir muchas noches", comentó en la publicación del blog de Aaronson.

Luego, en 2018, Juan pensó en usar el teorema de alternancia de Cauchy, una declaración matemática de hace 200 años, que conecta los valores propios de una matriz con una submatriz, lo que quizás lo convierte en una herramienta ideal para estudiar la relación entre un cubo y un subconjunto de sus vértices. Juan decidió solicitar una beca de la State Science Foundation para explorar más esta idea.

Luego, el mes pasado, sentado en un hotel en Madrid y completando una solicitud de subvención, de repente se dio cuenta de que podía extender el uso de este enfoque hasta el final, simplemente cambiando los signos de algunos números de la matriz. De esta manera, pudo demostrar que en cualquier conjunto de más de la mitad de los vértices de un cubo n-dimensional existirá un punto asociado con al menos √n otros puntos, y la hipótesis de sensibilidad se deduce inmediatamente de este resultado.

Cuando Matthew recibió el trabajo de Juan por correo, su primera reacción fue "¡Uy!", Dijo. "Cuando una tarea ha existido durante 30 años y todos lo saben, su prueba debe ser muy larga y compleja, o muy profunda". Ella abrió el archivo con el trabajo, esperando no entender nada.

Sin embargo, la prueba fue lo suficientemente simple como para que Matthew y otros investigadores pudieran digerirla de una vez. "Creo que este otoño, los estudiantes le dirán como parte de una conferencia en cada curso de maestría en combinatoria", escribió en Skype.

El resultado de Juan resultó ser aún más fuerte de lo necesario para probar esta hipótesis, y esta fuerza debería darnos nuevas ideas sobre medidas de complejidad. "Se ha agregado a nuestro kit de herramientas y puede ayudar a responder otras preguntas relacionadas con las funciones booleanas", dijo Cenedio.

Pero lo más importante, el resultado de Juan nos permite detener todas las preocupaciones sobre si la sensibilidad es un extraño extraño en el mundo de las medidas de complejidad, dijo Cenedio. "Creo que por la noche, al conocer estos resultados, muchos pudieron dormir en paz".