Jugando con números complejos

Hola

Otro ensayo Esta vez juguemos con números complejos, con fórmulas y su visualización.

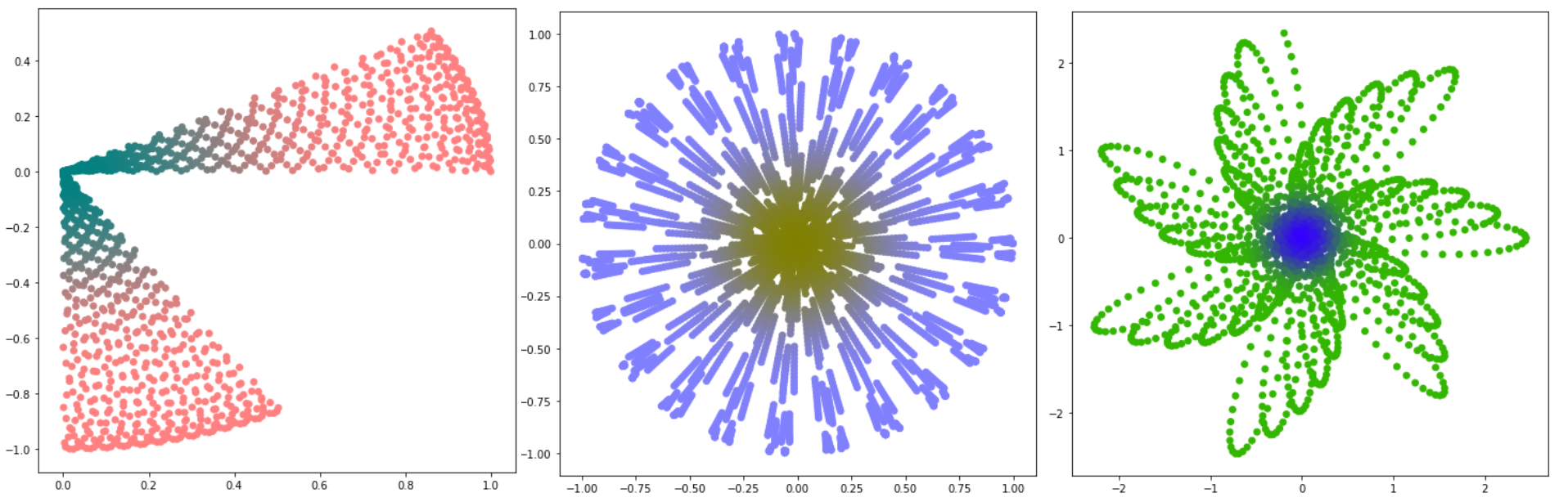
Idea

Un número complejo es una cierta extensión de un número real, de hecho, un vector para el que se define un conjunto completo de axiomas. Cualquier número complejo (y por lo tanto real) puede escribirse como $$$z = a + bi$donde a es la parte real, b es la parte imaginaria, i es la raíz de la ecuación $$$x ^ {2} = - 1$. Se definen muchas operaciones para él, que se definen para un número real, por ejemplo, $$$z_1 + z_2 = a_1 + a_2 + (b_1 + b_2) i$. Curiosamente, si haces varias operaciones con ellos, sube a un poder, multiplica, etc., y luego toma $$$Re (z)$(parte real) para el eje Ox, y $$$Im (z)$(parte imaginaria) para el eje Oy, puede obtener imágenes divertidas.

Por cierto, a mí mismo se me ocurrieron las siguientes fórmulas.

Función de visualización

Rutina La función, que de acuerdo con esta función iterativa dibuja todo en el campo:

import random import numpy as np def vis(A, f, step=1.0, c=None): x = [] y = [] for B in np.arange(0, A, step): v = f(A, B) x.append(v.real) y.append(v.imag) plt.figure(figsize=[8, 8]) mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5 x = np.array(x) / mxabs y = np.array(y) / mxabs if c is None: plt.scatter(x, y) else: plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))]) plt.show() 

Todas nuestras funciones dependen de dos parámetros A y B. Además, iteramos sobre B dentro de vis (), y A es el parámetro global de la función.

La función de rizo

$$

$$f (A, B) = Bsin (B) * e ^ {iBcos (A)}$$

Su declaración en python:

 def func_1(A, B): return math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

Y correr

 A = 121.5 vis(A, func_1, step=0.1) 

Y el resultado para A = 121.5:



Y para A = 221.5:



Tenga en cuenta que estos números no se deducen del cálculo de una integral definida en una variedad uniforme y otras palabras inteligentes que no tienen sentido en este contexto. Estos son números realmente aleatorios, y todavía hay exactamente infinito de diferentes A, lo que resulta en belleza.

Necesito pintar

Declaramos una función de color (una función que devuelve una tupla de tres números en coordenadas):

 def sigm(x): #         0  1 return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2 color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2)) color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5) 

Elija el parámetro aleatorio A, que sea 149:

 vis(149, func_1, step=0.1, c=color_1) 

Función de gansos

Los gansos se describen a continuación:

$$

$$f (A, B) = cos (B) sin (B) * B * e ^ {iBcos (A)}$$

Declaración de Python:

 def func_2(A, B): return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

Su resultado para A = 106:

Función focaccia

$$

$$f (A, B) = cos (B (A + 1)) * e ^ {iBcos (A)}$$

 def func_3(A, B): return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A))) 

 vis(246, func_3, step=0.1, c=color_2) 

 vis(246, func_3, step=0.1, c=color_2) 

Función sin título

$$

$$f (A, B) = Bsin (A + B) * e ^ {iBsin (A)}$$

 color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2)) vis(162, func_4, step=0.1, c=color_3) 

 vis(179, func_4, step=0.1, c=color_3) 

Fórmula de belleza

$$

$$f (A, B) = cos (B (A + 1)) ^ {\ frac {3} {2}} * e ^ {iBcos (A)}$$

 def func_5(A, B): return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A))) 

 color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2)) vis(345, func_5, step=0.1, c=color_4) 

 vis(350, func_5, step=0.1, c=color_4) 

Eso es todo por ahora.