"Tecnología" de obtención de ecuaciones de dinámica de TAU. ¿Y por qué la identificación del sistema es una mierda y las reglas de "física honesta"

Cuando discutimos el artículo anterior sobre el diseño orientado a modelos, surgió una pregunta razonable: si usamos los datos del experimento, pero ¿es posible hacerlo aún más fácil, poner los datos en Identificación del sistema y obtener el modelo del objeto sin preocuparse por la física? ¿Sin estudiar todo tipo de fórmulas de varios pisos de Navier-Stokes, Bernoulli y otras brújulas de calibre con Rabinovichi? Probamos el objeto, obtuvimos el resultado.



Presentamos el modelo de misil FAU2 como una función de transferencia única, puedes verlo aquí ... Y, al parecer, todo funcionó. ¿Por qué necesitamos primero estudiar análisis matemático y cálculo diferencial cuando hay un botón mágico que obtiene el modelo de las pruebas?

De hecho, este enfoque puede aplicarse, pero esto requiere dos condiciones:

• El objeto ya debería ser (no apto para objetos diseñados).
• Los datos de medición deben ser completos y confiables.

En cualquier otro caso, "querían lo mejor, resultó como siempre" (c).
Por ejemplo, en este artículo sobre la simulación de un accionamiento eléctrico, se muestra que "con un cierto valor umbral de la precisión de los instrumentos de medición, el modelo de accionamiento se vuelve inidentificable, lo que conduce a una pérdida de capacidad de control e incapacidad para diagnosticar"
En el mismo artículo, analizaremos la magia y la magia de crear modelos en forma de funciones de transferencia desde TAU, y luego llevaremos a cabo una sesión para exponer esta magia.

Entonces primero la magia

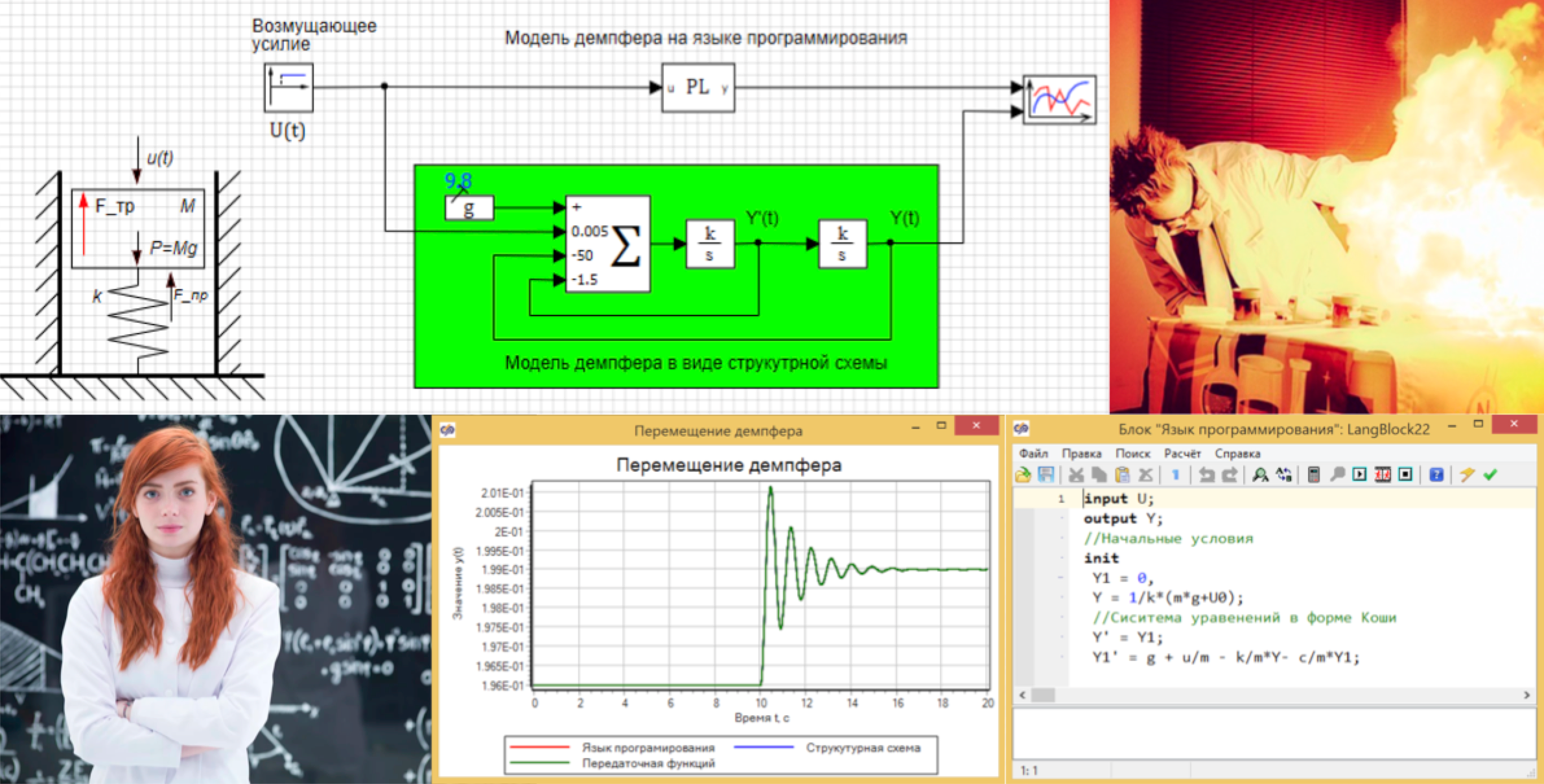
Echemos un vistazo a un ejemplo simple. Tenemos un modelo de amortiguador mecánico. Este es un pistón en un resorte, se mueve dentro del cilindro, puede moverse hacia arriba y hacia abajo. Su posición es la función Y (t) que nos interesa, la fuerza perturbadora (U (t)) actúa sobre ella desde arriba y la fuerza de fricción viscosa actúa sobre las paredes del pistón. (Ver Fig. 1)


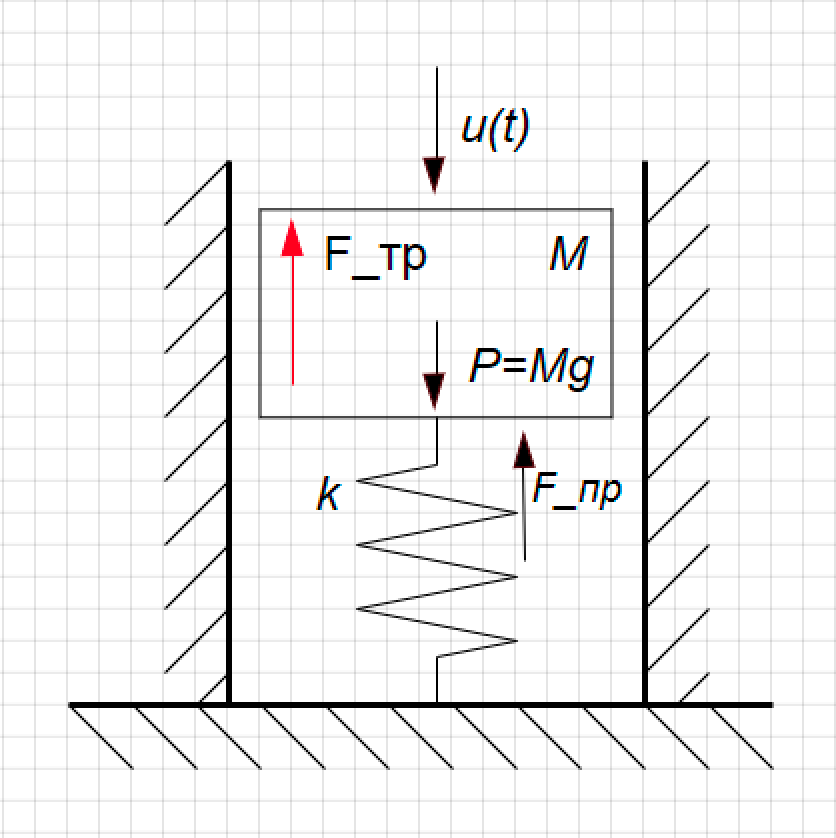Figura 1. El diseño del amortiguador.

Derivamos la función de transferencia para este enlace.

Aquellos Jedi que ya están familiarizados con la magia de las funciones de transferencia pueden omitir esta parte e ir directamente a exponer la magia, y para los jóvenes Padawans revelaremos toda la tecnología para obtener ecuaciones dinámicas.

Según la segunda ley de Newton, la aceleración del cuerpo es proporcional a la suma de las fuerzas que actúan sobre el cuerpo:

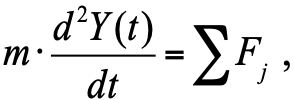
, (1)
donde m es el peso corporal; F _j - fuerzas que actúan sobre el cuerpo (pistón amortiguador).
Sustituyendo en la ecuación (1) todas las fuerzas de acuerdo con la Fig. 1, tenemos:

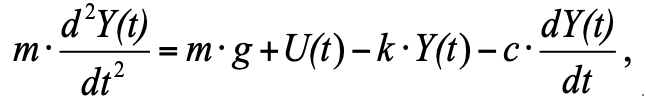
(2)
donde:
Y (t) es la posición del pistón;
P = m ∙ g - gravedad;
F_pr = k ∙ Y (t) - fuerza de resistencia del resorte;
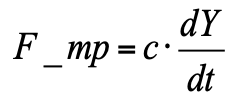
- fuerza de fricción viscosa (proporcional a la velocidad del pistón).
Dimensiones de fuerzas y coeficientes incluidos en la ecuación (2):


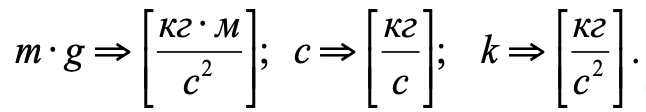
Creemos que a tiempo cero el pistón está en equilibrio. Entonces, la posición inicial del pistón es y ₀ en equilibrio, donde la velocidad y la aceleración son 0, se puede calcular a partir de la ecuación 2.



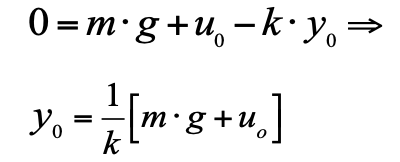
Esta ecuación le permite calcular en qué posición estará el pistón con diferentes cargas. Esta característica estática: fuerza aplicada - desplazamiento recibido. Su apariencia para nuestro sistema es extremadamente simple (ver Fig. 2):


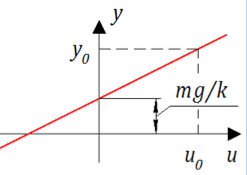Figura 2. Característica estática del amortiguador.

Parece que aquí está la felicidad: una línea simple, cuando aplicaba fuerza, recibía desplazamiento. Pero ahí estaba! No estamos interesados ​​en la posición final del pistón, sino en el proceso de transición de un estado a otro.

Para analizar el proceso transitorio, se creó la teoría del control automático de TAU. Según una típica "tecnología para crear modelos" según esta teoría, se propone considerar el sistema no en valores absolutos, sino en desviaciones del estado de equilibrio. Tal afirmación simplifica la solución y la construcción. Y, de hecho, si reemplazamos los valores absolutos con desviaciones, obtenemos:


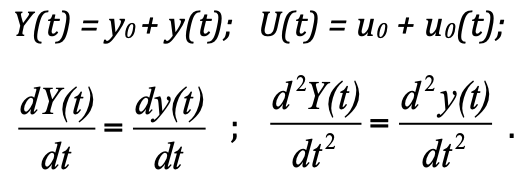F_pr = k ∙ (y ₀ + y (t)) = k ∙ y ₀ + k ∙ y (t) es la fuerza de resistencia del resorte;
- fuerza de fricción.
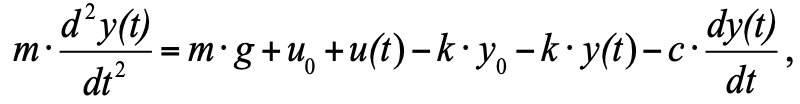
pero como aceptamos que en el momento inicial tenemos un estado de equilibrio, y la suma de las tres fuerzas en el estado de equilibrio es cero, podemos eliminarlas de la ecuación, y como resultado obtenemos:

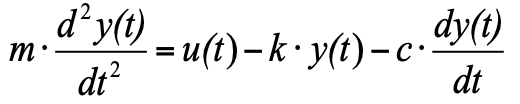
(4)
Para traducir la ecuación a la forma de acuerdo con el canon de TAU, debe dividir toda la ecuación por k para que el coeficiente y, el valor de la variable de salida sea igual a 1, y transferir los factores con los valores de salida de y (t) al lado derecho y los valores de entrada al lado izquierdo influye en u (t) :

(5)
Esta ecuación ya se puede escribir en forma de operador:

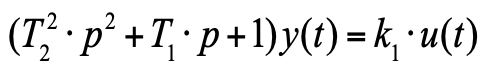
(6)
donde:


p = d / dt es el operador de diferenciación. Tenga en cuenta que las dimensiones de los coeficientes tienen la dimensión y el significado de las constantes de tiempo:



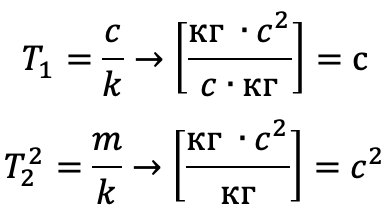
Una función de transferencia para tal ecuación [6] tiene la forma:


Ahora, ante sus propios ojos, obtuvimos la función de transferencia en forma de un bloque de las ecuaciones de la física, y, además, el bloque resultante es un enlace oscilatorio estándar de TAU.

Para mí personalmente, la magia aquí es la apariencia mágica de las características estáticas, partes del sistema, masa del pistón, elasticidad del resorte, fricción en las paredes) del objeto, una característica temporal de los procesos transitorios en el sistema que apareció mágicamente.

Consulta las fórmulas con el modelo

Como Maxim Andreev me enseñó, al crear modelos dinámicos "¡El final es la cabeza de todo!" ( vea aquí el segundo principio de modelado - "comenzar desde el final" ):

Y al final de la función, tenemos movimiento.

Por lo tanto, imagine la ecuación 2 en forma de Cauchy, para moverse.

La forma de Cauchy es cuando a la izquierda se derivan de las funciones que nos interesan, a la derecha se encuentran expresiones para su cálculo. Dado que la derivada en la ecuación es de segundo grado, introduciendo una nueva variable Y1, la tasa de cambio de posición (velocidad de desplazamiento), obtenemos un sistema de dos ecuaciones en forma de Cauchy:



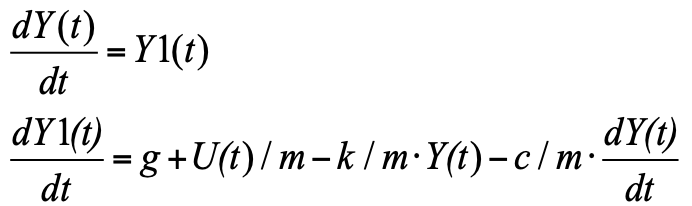
Esta ecuación puede simplemente escribirse en el bloque "Lenguaje de programación" y obtener el modelo (ver Fig. 3):


Figura 3. Un modelo de amortiguador en un lenguaje de programación.

Como entrada, usamos el valor de la fuerza U, la salida del bloque es el desplazamiento Y, la posición inicial viene dada por la fórmula 3. Todas las variables se configuran como señales globales para el proyecto:


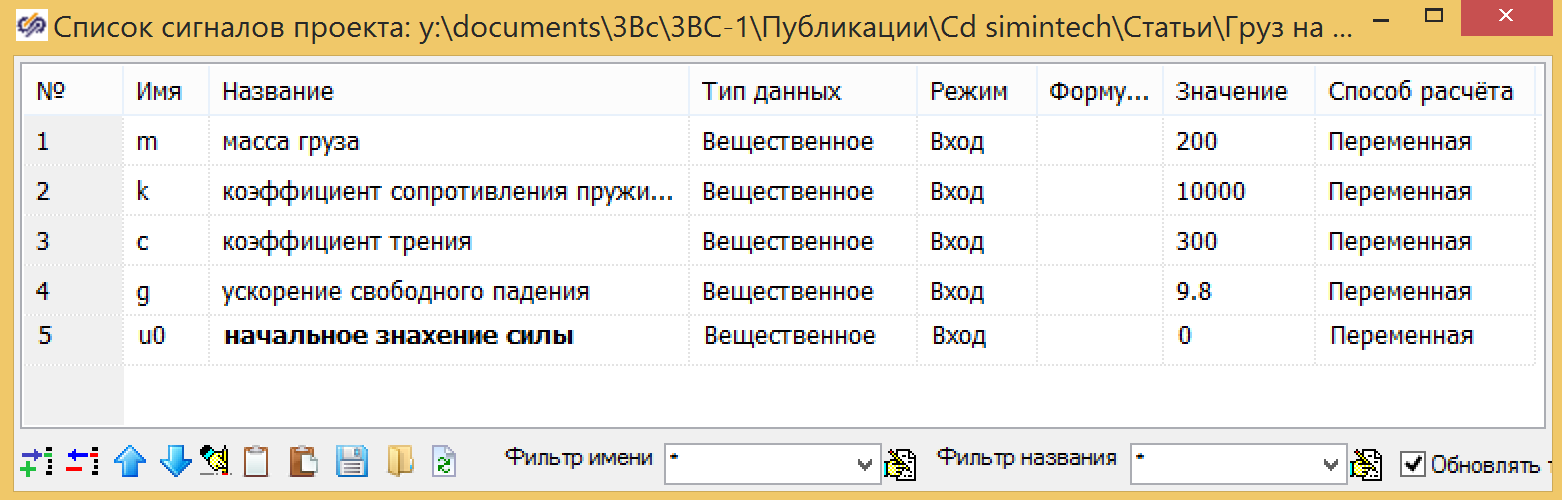Figura 4. Variables globales del proyecto.

El modelo de amortiguador también se puede crear en forma de estructura, en la Figura 5, que muestra un modelo de amortiguador paralelo creado a partir de bloques estándar, en el que la condición inicial está en el integrador en la salida (ver Fig. 6), y los coeficientes se ingresan en el sumador (ver Fig. 7)


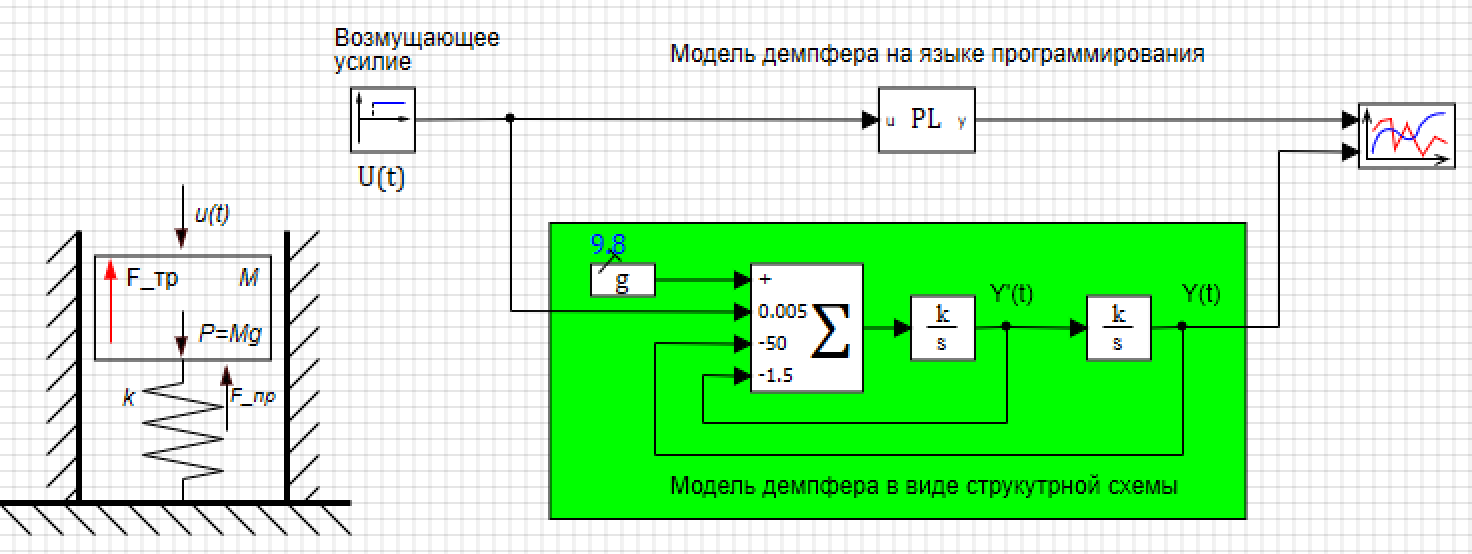Figura 5. Amortiguador en un lenguaje de programación y en forma de diagrama estructural.


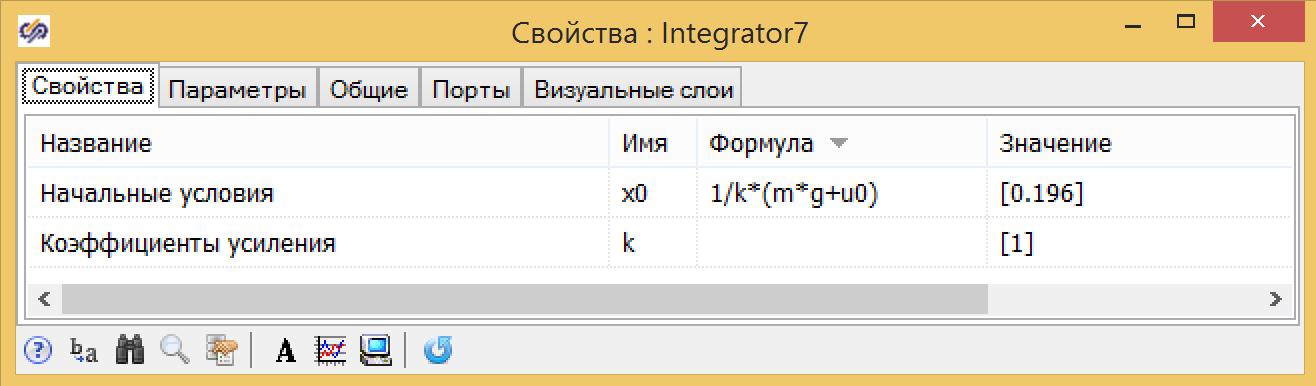Figura 6. Propiedad del integrador con condiciones iniciales.


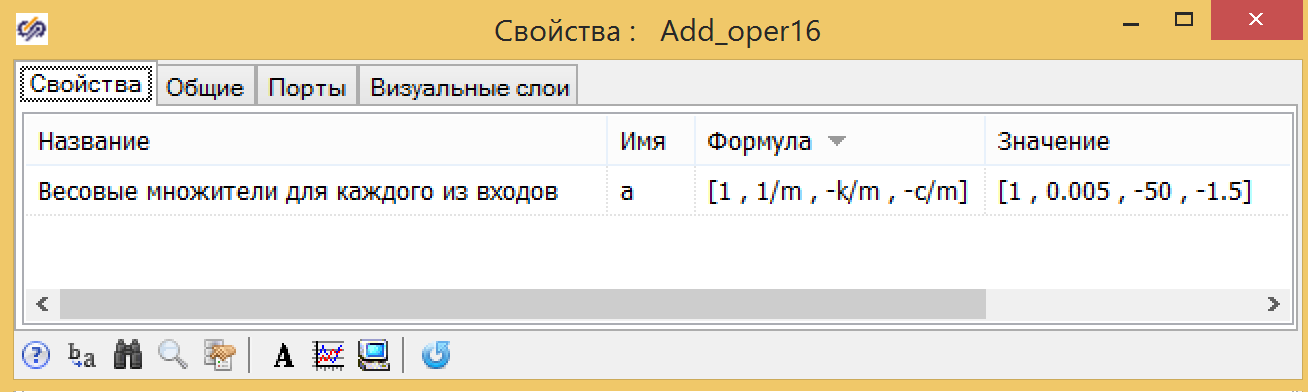Figura 7. Propiedades del sumador con coeficientes.

Establecemos la acción perturbadora durante 10 segundos, cambiando la fuerza de actuación de 0 a 30, en un salto, y nos aseguramos de que los dos modelos muestren el mismo resultado (ver Fig. 8).


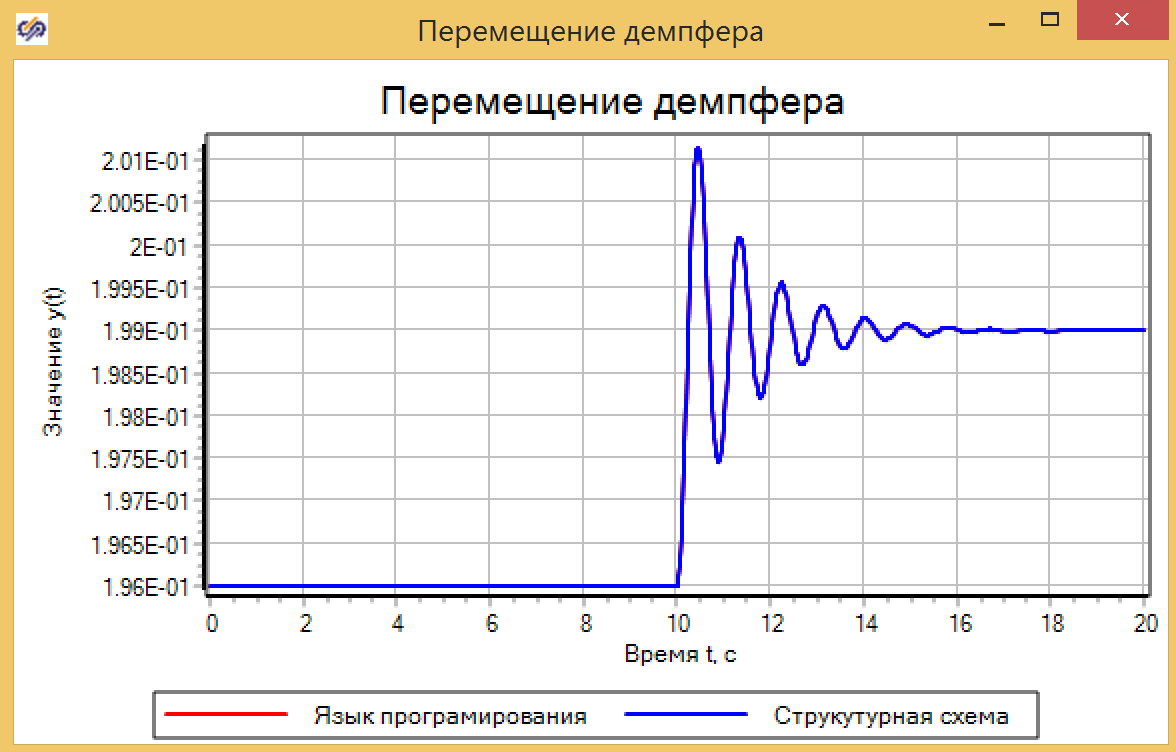Figura 8. Moviendo el amortiguador.

Verifiquemos el modelo en forma de una función de transferencia en forma general y en forma de un enlace oscilante, que es este sistema. Para hacer esto, ensamblamos el circuito, como se muestra en la Figura 9.


Figura 9. Dos modelos de amortiguadores en forma de funciones de transferencia.

Debe tenerse en cuenta que compilamos el diagrama en desviaciones, por lo tanto, para obtener el valor absoluto, es necesario agregar una constante: la posición inicial del pistón.

Para la función de transferencia (fórmula 7) usamos las mismas constantes y expresiones globales obtenidas anteriormente para k ₁ , T ₁ , T ₂ (ver Fig. 10).


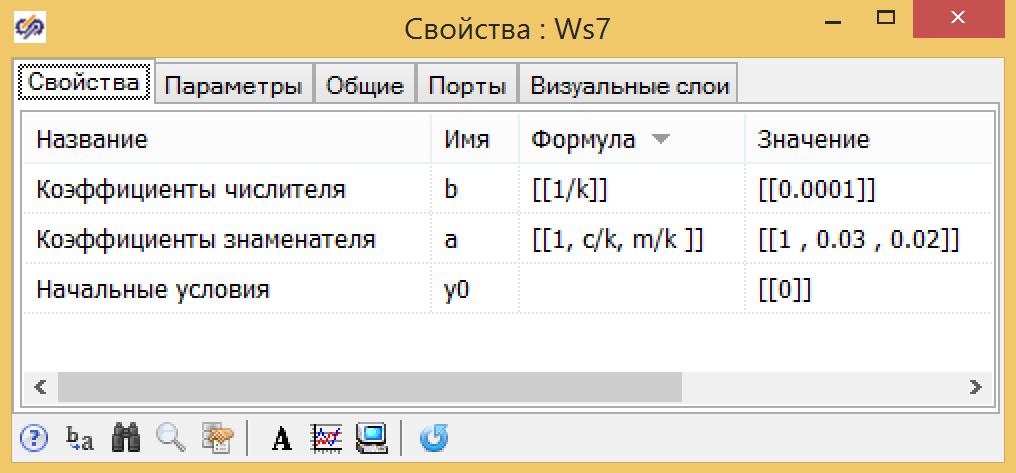Figura 10. Parámetros de la función de transferencia de la forma general.

Para los parámetros del enlace vibratorio, las fórmulas son un poco más complicadas, pero todas también se pueden expresar en términos de parámetros globales: masa del pistón - m, coeficiente de arrastre del resorte - k, coeficiente de fricción - s (ver Fig. 11).


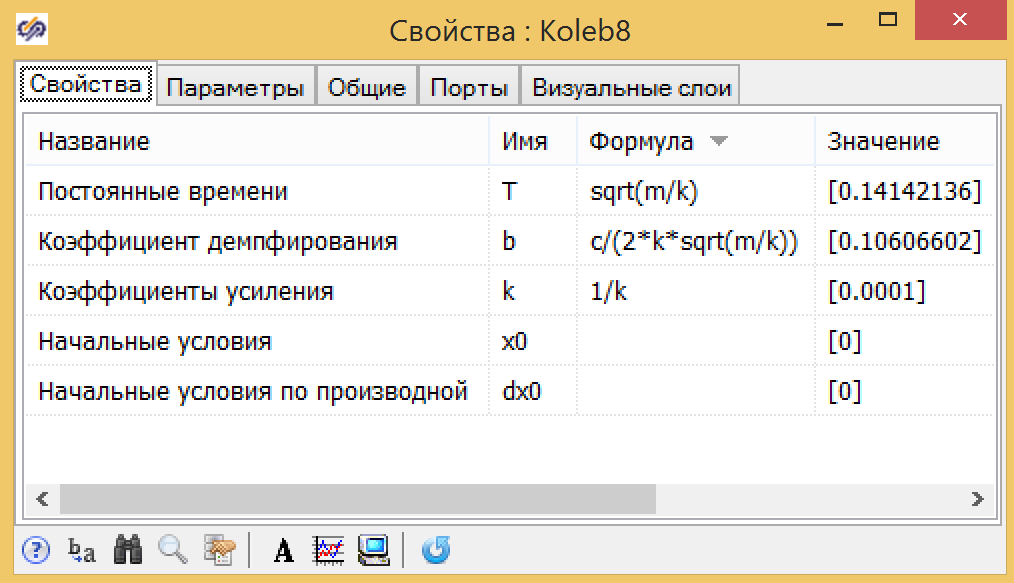Figura 11. Parámetros del enlace vibratorio.

Los gráficos de transición muestran (ver Figura 12) que la magia TAU realmente funciona. La función de transferencia da exactamente los mismos resultados que un modelo basado en ecuaciones físicas.


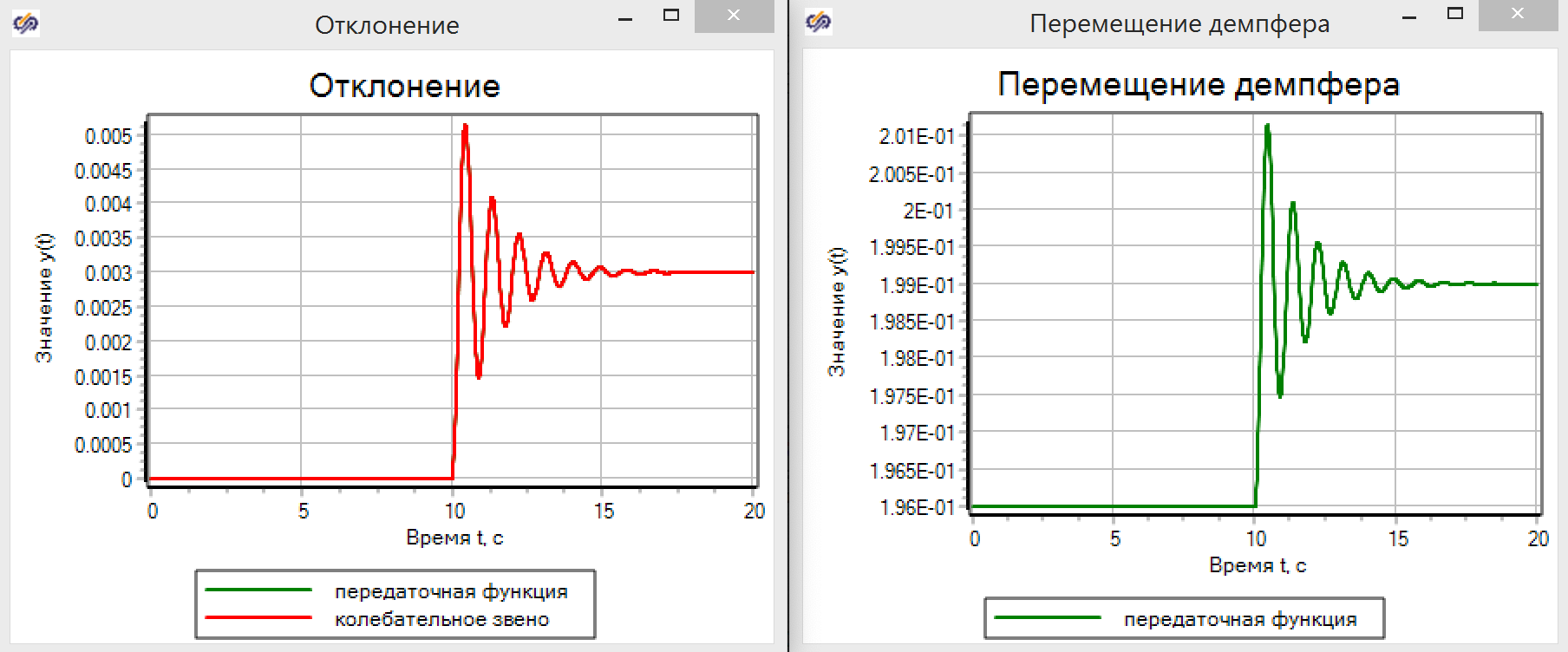Figura 12. Desplazamiento del amortiguador en modelos TAU.

Imagine que no tenemos un modelo y usamos una unidad de identificación de acuerdo con los datos obtenidos del experimento. Existe toda una tecnología de análisis de datos y funciones de transferencia, pero como parte del artículo y como ejemplo, conectaremos el componente básico de la función de transferencia al modelo en forma de lenguaje de programación, como se muestra en la Figura 13. Creemos que tenemos un modelo de "caja negra", y No sabemos lo que hay dentro.


Figura 13. El esquema de conexión del pseudoidentificador.

Como resultado del análisis de nuestro bloque en un lenguaje de programación, obtuvimos una función de transferencia, que prácticamente no difiere de la inicial, derivada de las ecuaciones (ver Fig. 14.). Compare con la figura 10. ¡Aquí hay un botón mágico!


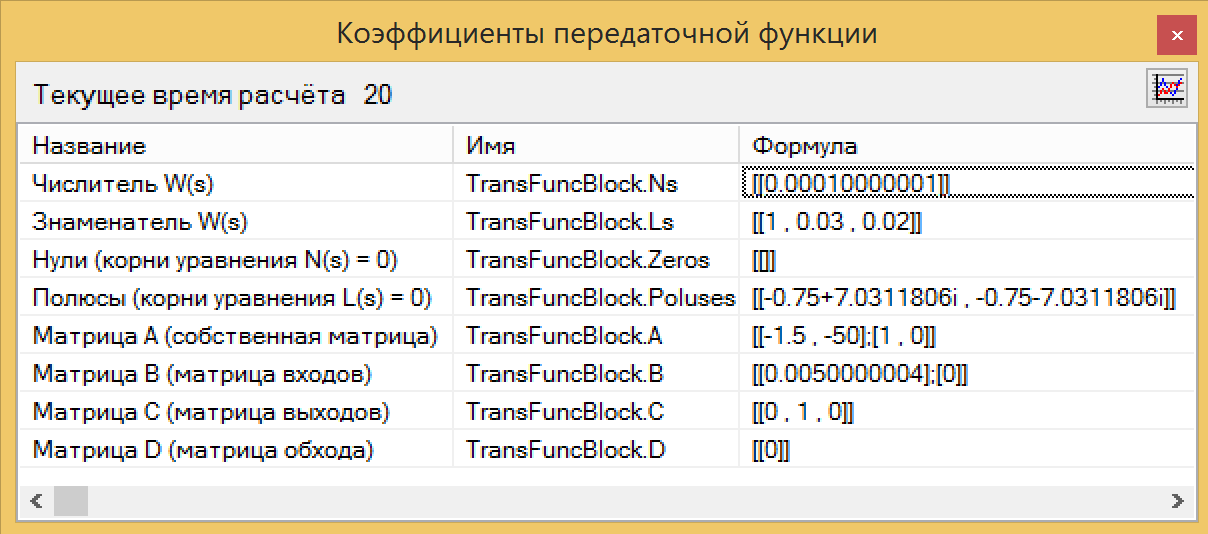Figura 14. Identificación de la función de transferencia.

Los valores de numerador y denominador pueden copiarse directamente del bloque de identificación, pegarse en el bloque de función de transferencia y asegurarse de que los gráficos coincidan. La magia TAU funciona.

Sesión de exponer magia

Entonces, ¿por qué no siempre puedes usar la Identificación del sistema para un proceso de diseño orientado a modelos cuando todo es tan mágico?

Para comprender el inconveniente de los modelos obtenidos al identificar la caja negra de Identificación del sistema, intente responder una pregunta simple: ¿cuál será la desviación del amortiguador cuando la masa del pistón se incremente en un 30%?

Y luego resulta que no todos los yogures son igualmente útiles.

Si tiene ecuaciones honestas, simplemente cambie la masa de la carga en las variables globales del proyecto y obtenga un nuevo proceso de transición y una nueva función de transferencia.



En el caso de que, en lugar de las ecuaciones honestas de la física, ya tenga la función de transferencia construida en función de los resultados del experimento, debe ejecutar nuevamente y hacer el experimento para comprender cómo el cambio en la masa afectará el comportamiento del modelo. Como dicen, una cabeza mala no da descanso a las piernas.

Conclusiones:

1. Sentarse y pensar en las ecuaciones de la física siempre es más beneficioso y más barato que experimentar.
2. Un modelo derivado de las ecuaciones físicas de los procesos es mucho más sabroso y más útil que las funciones de transferencia.
3. El experimento debe aclarar coeficientes desconocidos o parámetros difíciles de medir.
4. ¡Aprende física y serás feliz!

El archivo con el modelo de amortiguador para experimentos se puede tomar aquí ...