Esta es una instrucción paso a paso para la clasificación de imágenes multiespectrales del satélite Landsat 5. Hoy, en varias áreas, el aprendizaje profundo domina como una herramienta para resolver problemas complejos, incluidos los geoespaciales. Espero que esté familiarizado con los conjuntos de datos satelitales, en particular, Landsat 5 TM. Si está un poco familiarizado con los algoritmos de aprendizaje automático, esto lo ayudará a aprender rápidamente este manual. Y para aquellos que no entienden, será suficiente saber que, de hecho, el aprendizaje automático consiste en establecer relaciones entre varias características (un conjunto de atributos X) de un objeto con su otra propiedad (valor o etiqueta, la variable objetivo Y). Alimentamos el modelo con muchos objetos para los que se conocen las características y el valor del indicador / clase objetivo del objeto (datos etiquetados) y lo entrenamos para que pueda predecir el valor de la variable objetivo Y para nuevos datos (sin marcar).
¿Cuál es el principal problema con las imágenes satelitales?
Dos o más clases de objetos (por ejemplo, edificios, lotes baldíos y pozos de cimentación) en imágenes de satélite pueden tener las mismas características espectrales del valor, por lo tanto, en los últimos veinte años, su clasificación ha sido una tarea difícil.
Debido a esto, es posible usar modelos clásicos de aprendizaje automático con y sin un maestro, pero su calidad estará lejos de ser ideal. Siempre tienen los mismos inconvenientes. Considere un ejemplo:
Si usa una línea vertical como clasificador y la mueve a lo largo del eje X, entonces clasificar imágenes de casas no será fácil. Los datos se distribuyen de manera que es imposible separarlos en clases usando una línea vertical (en tales casos se dice que "los objetos de diferentes clases no son linealmente separables"). ¡Pero esto no significa que las casas no se puedan clasificar en absoluto!
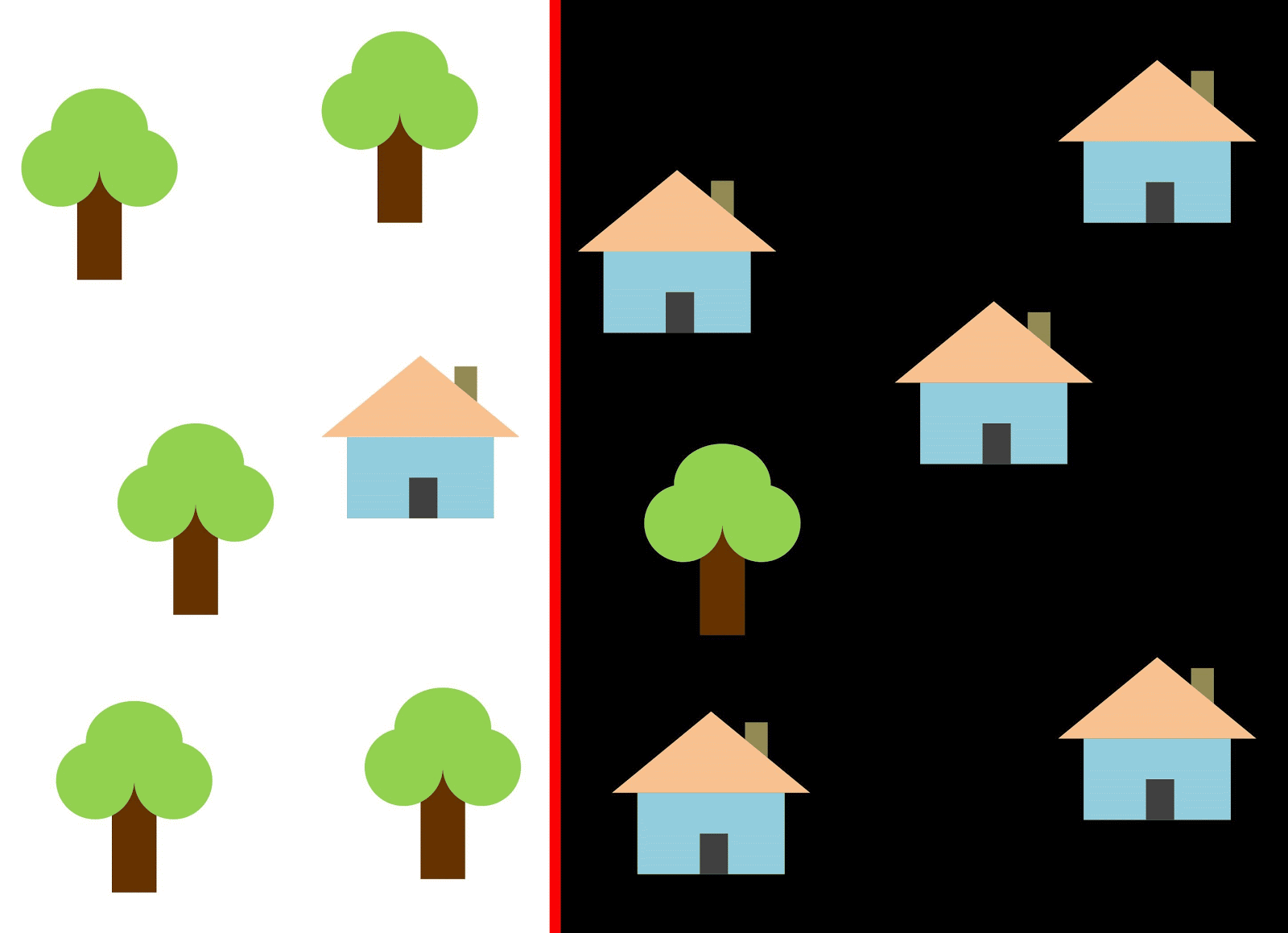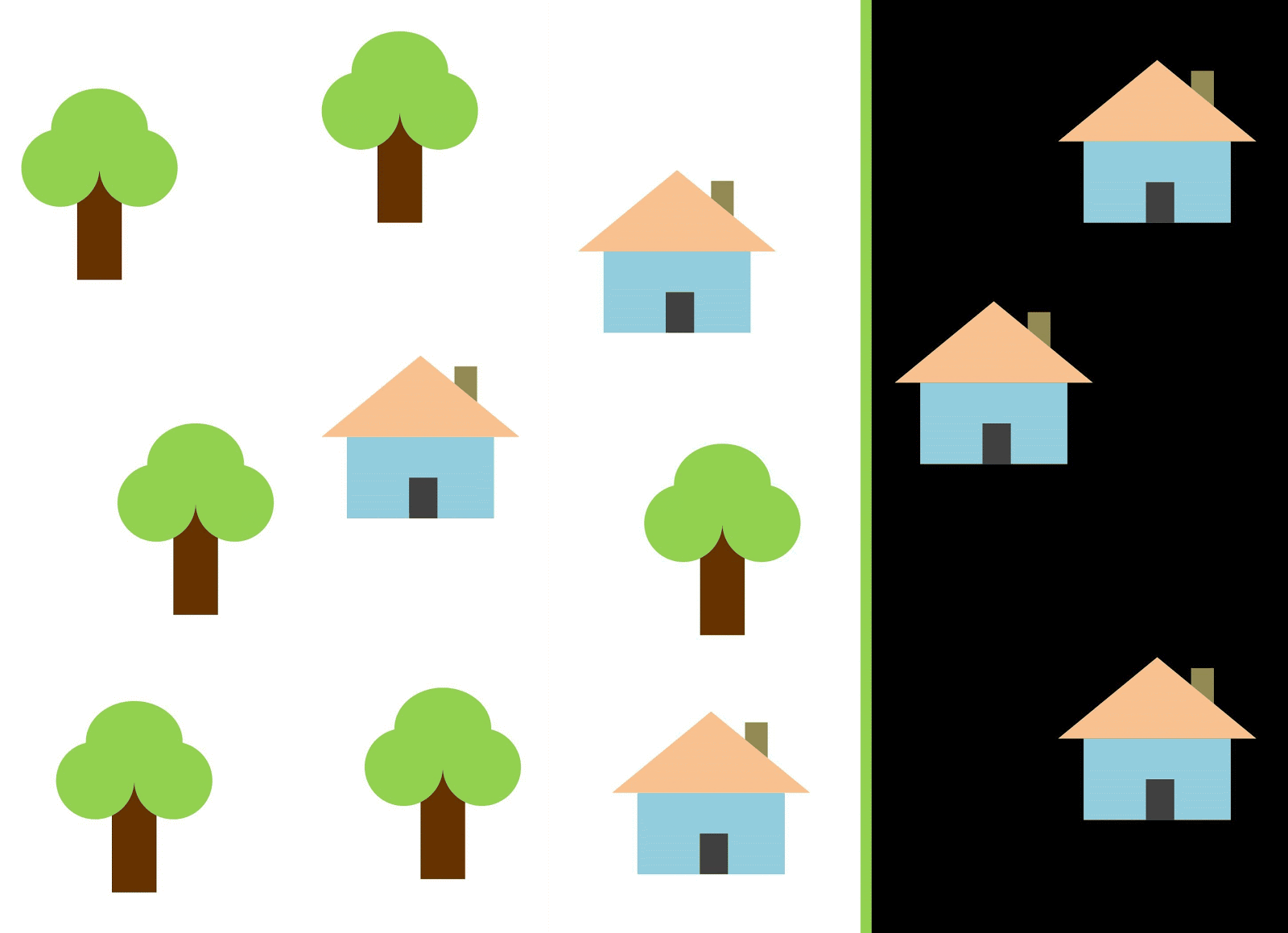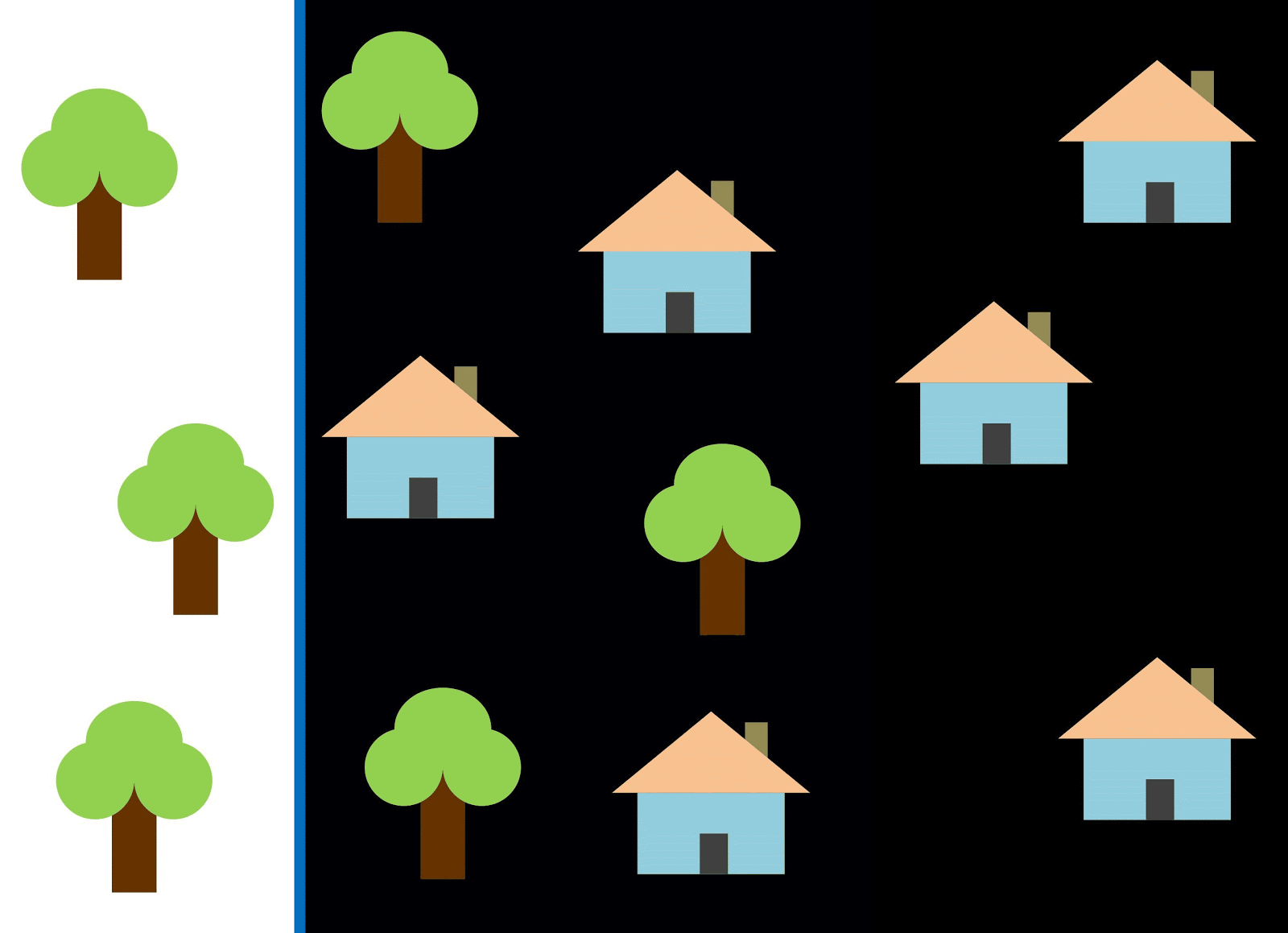
Usemos la línea roja para separar las dos clases. En este caso, el clasificador identificó la mayoría de las casas, pero una casa no fue asignada a su clase, y tres árboles más fueron asignados por error a las "casas". Para no perderse una sola casa, puede usar el clasificador en forma de línea azul. Entonces todo estará cubierto en casa, es decir, decimos que la métrica de retiro (plenitud) es alta. Sin embargo, no todos los valores clasificados resultaron ser casas, es decir, al mismo tiempo obtuvimos un valor bajo de la métrica de precisión. Si usamos la línea verde, entonces todas las imágenes clasificadas como casas realmente serán casas, es decir, el clasificador mostrará una alta precisión. En este caso, la plenitud será menor, ya que las tres casas no se contabilizarán. En la mayoría de los casos, tenemos que encontrar un compromiso entre la precisión y la integridad.
Este problema de casas y árboles es similar al problema con edificios, lotes baldíos y pozos. La prioridad de las métricas de clasificación de imágenes satelitales puede variar según la tarea. Por ejemplo, si necesita asegurarse de que todos los territorios construidos se clasifiquen como edificios sin excepción, y está listo para soportar la presencia de píxeles de otras clases con firmas similares, que también se clasificarán como edificios, entonces necesita un modelo con una alta integridad. Y si es más importante para usted clasificar un edificio, sin agregar píxeles de otras clases, y está listo para abandonar la clasificación de territorios mixtos, elija un clasificador con alta precisión. En el caso de casas y árboles, el modelo habitual usará la línea roja, manteniendo un equilibrio entre precisión e integridad.
Datos utilizados
Como signos, utilizaremos los valores de seis rangos (banda 2 - banda 7) de la imagen de Landsat 5 TM e intentaremos predecir la clase de desarrollo binario. Para capacitación y pruebas, se utilizarán datos multiespectrales (imágenes y una capa con una clase de construcción binaria) con Landsat 5 para 2011 para Bangalore. Y para la predicción se utilizarán datos Landsat 5 multiespectrales obtenidos en 2005 en Hyderabad.
Dado que usamos datos etiquetados para la enseñanza, esto se llama enseñanza con el maestro.
Datos de entrenamiento multiespectral y la capa binaria correspondiente con desarrollo.Para crear una red neuronal, usaremos Python, la biblioteca de Google Tensorflow. También necesitaremos estas bibliotecas:
- pyrsgis : para leer y escribir GeoTIFF.
- scikit-learn : para preprocesamiento de datos y evaluación de precisión.
- numpy : para operaciones básicas con matrices.
Y ahora, sin más preámbulos, escribamos el código.
Coloque los tres archivos en un directorio, escriba la ruta y los nombres de los archivos de entrada en el script y luego lea los archivos GeoTIFF.
import os from pyrsgis import raster os.chdir("E:\\yourDirectoryName") mxBangalore = 'l5_Bangalore2011_raw.tif' builtupBangalore = 'l5_Bangalore2011_builtup.tif' mxHyderabad = 'l5_Hyderabad2011_raw.tif'
El módulo
raster del paquete
pyrsgis lee los datos de geolocalización GeoTIFF y los valores de números digitales (DN) como matrices NumPy separadas. Si está interesado en los detalles, lea
aquí .
Ahora mostramos el tamaño de los datos leídos.
print("Bangalore multispectral image shape: ", featuresBangalore.shape) print("Bangalore binary built-up image shape: ", labelBangalore.shape) print("Hyderabad multispectral image shape: ", featuresHyderabad.shape)
Resultado:
Bangalore multispectral image shape: 6, 2054, 2044 Bangalore binary built-up image shape: 2054, 2044 Hyderabad multispectral image shape: 6, 1318, 1056
Como puede ver, las imágenes de Bangalore tienen el mismo número de filas y columnas que en la capa binaria (correspondiente al edificio). El número de capas en imágenes multiespectrales en Bangalore y Hyderabad también coincide. El modelo aprenderá a decidir qué píxeles pertenecen al edificio y cuáles no, en función de los valores correspondientes para los 6 espectros. Por lo tanto, las imágenes multiespectrales deben tener el mismo número de características (rangos) enumeradas en el mismo orden.
Ahora convertimos las matrices en bidimensionales, donde cada fila representa un píxel separado, porque esto es necesario para la operación de la mayoría de los algoritmos de aprendizaje automático. Haremos esto usando el módulo de
pyrsgis paquete
pyrsgis .
Esquema de reestructuración de datos. from pyrsgis.convert import changeDimension featuresBangalore = changeDimension(featuresBangalore) labelBangalore = changeDimension (labelBangalore) featuresHyderabad = changeDimension(featuresHyderabad) nBands = featuresBangalore.shape[1] labelBangalore = (labelBangalore == 1).astype(int) print("Bangalore multispectral image shape: ", featuresBangalore.shape) print("Bangalore binary built-up image shape: ", labelBangalore.shape) print("Hyderabad multispectral image shape: ", featuresHyderabad.shape)
Resultado:
Bangalore multispectral image shape: 4198376, 6 Bangalore binary built-up image shape: 4198376 Hyderabad multispectral image shape: 1391808, 6
En la séptima línea, extrajimos todos los píxeles con un valor de 1. Esto ayuda a evitar problemas con los píxeles sin información (NoData), que a menudo tienen valores extremadamente altos o bajos.
Ahora dividiremos los datos en muestras de capacitación y validación. Esto es necesario para que el modelo no vea los datos de prueba y funcione igual de bien con la nueva información. De lo contrario, el modelo se volverá a entrenar y funcionará bien solo en los datos de entrenamiento.
from sklearn.model_selection import train_test_split xTrain, xTest, yTrain, yTest = train_test_split(featuresBangalore, labelBangalore, test_size=0.4, random_state=42) print(xTrain.shape) print(yTrain.shape) print(xTest.shape) print(yTest.shape)
Resultado:
(2519025, 6) (2519025,) (1679351, 6) (1679351,) test_size=0.4
significa que los datos se dividen en capacitación y validación en una proporción de 60/40.
Muchos algoritmos de aprendizaje automático, incluidas las redes neuronales, necesitan datos normalizados. Esto significa que deben distribuirse dentro de un rango determinado (en este caso, de 0 a 1). Por lo tanto, para cumplir este requisito, normalizamos los síntomas. Esto se puede hacer extrayendo el valor mínimo y luego dividiéndolo por el diferencial (la diferencia entre los valores máximo y mínimo). Como el dataset Landsat es de ocho bits, los valores mínimo y máximo serán 0 y 255 (2
⁸ = 256 valores).
Tenga en cuenta que para la normalización siempre es mejor calcular los valores mínimos y máximos en función de los datos. Para simplificar la tarea, nos mantendremos en el rango de ocho bits por defecto.
Otra etapa del procesamiento preliminar es la transformación de la matriz de signos de dos dimensiones a tres dimensiones, de modo que el modelo perciba cada fila como un píxel separado (un objeto de aprendizaje separado).
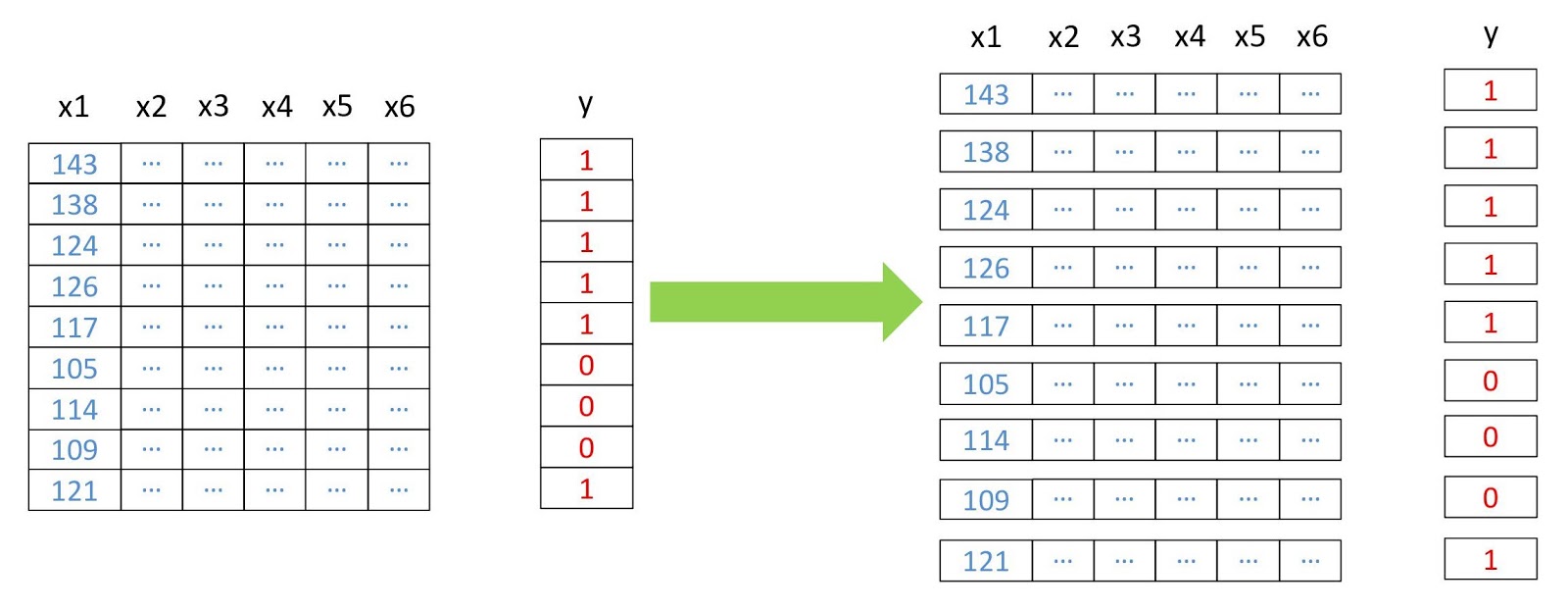
Resultado:
(2519025, 1, 6) (1679351, 1, 6) (1391808, 1, 6)
Todo está listo, ensamblemos nuestro modelo con
keras . Para comenzar, usemos el modelo secuencial, agregando capas una tras otra. Tendremos una capa de entrada con el número de nodos igual al número de rangos (
nBands ), en nuestro caso hay 6. También usaremos una capa oculta con 14 nodos y la
ReLu activación
ReLu . La última capa consta de dos nodos para definir una clase de construcción binaria con la
softmax activación
softmax , que es adecuada para mostrar un resultado categorizado. Lea más sobre las funciones de activación
aquí .
from tensorflow import keras
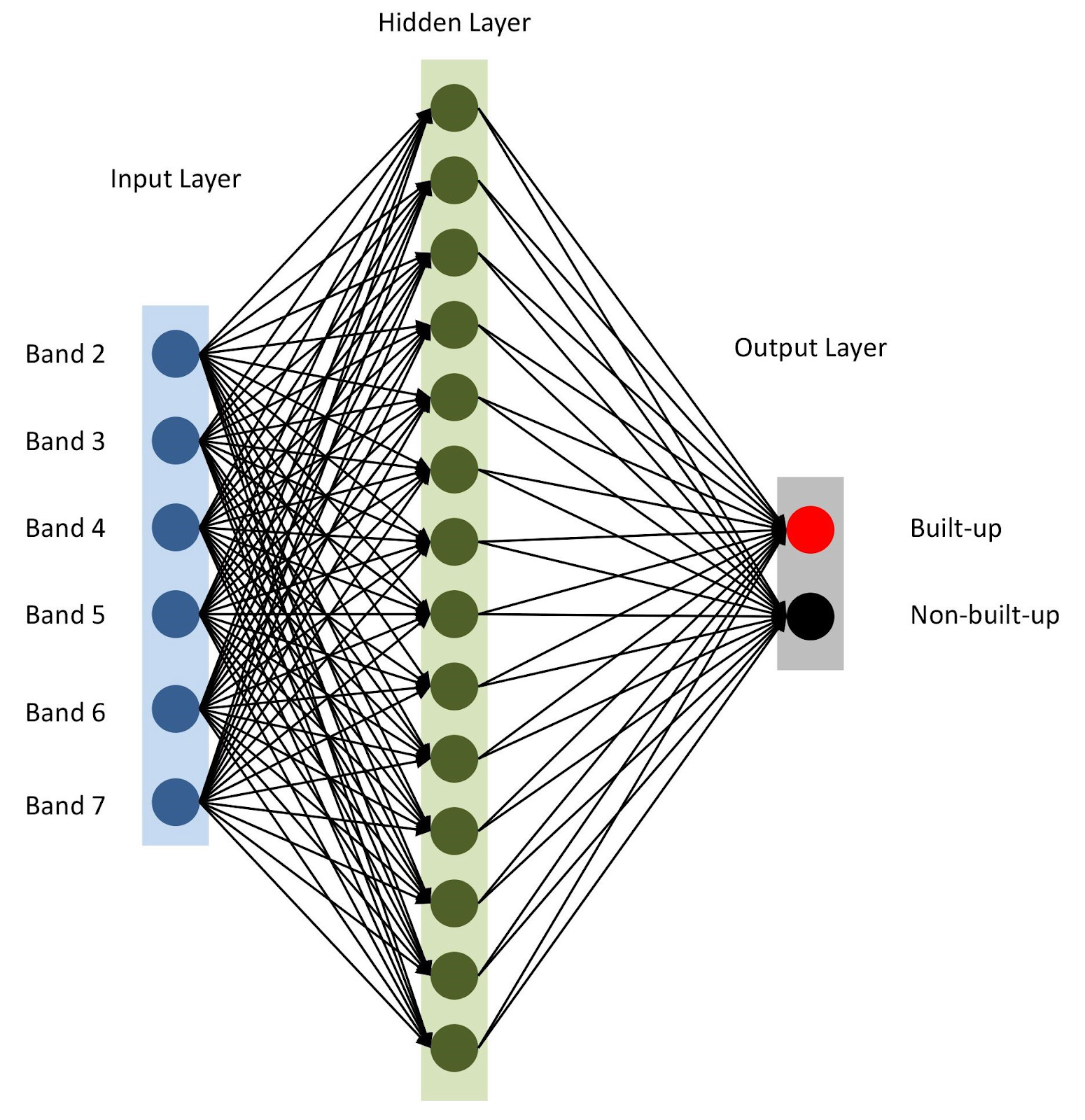Arquitectura de red neuronalComo se menciona en la línea 10, especificamos
adam como optimizador de modelo (hay varios
otros ). En este caso, utilizaremos la entropía cruzada como una función de pérdida (en.
categorical-sparse-crossentropy -
aquí se escribe más sobre esto). Para evaluar la calidad del modelo, utilizaremos la métrica de
accuracy .
Finalmente, comenzaremos a entrenar nuestro modelo para dos eras (o iteraciones) en
xTrain y
yTrain . Esto llevará algún tiempo, dependiendo del tamaño de los datos y la potencia de procesamiento. Esto es lo que verá después de la compilación:
Vamos a predecir los valores para los datos de validación que almacenamos por separado y calcular varias métricas de precisión.
from sklearn.metrics import confusion_matrix, precision_score, recall_score
La función
softmax genera columnas separadas para valores de probabilidad para cada clase. Utilizamos solo los valores para la primera clase ("hay un edificio"), como se puede ver en la sexta línea del código anterior. Evaluar el trabajo de los modelos de análisis geoespacial no es tan simple, a diferencia de otros problemas clásicos del aprendizaje automático. Será injusto confiar en un error total generalizado. La clave para un modelo exitoso es el diseño espacial. Por lo tanto, la matriz de confusión, la precisión y la integridad pueden dar una idea más correcta de la calidad del modelo.
Entonces, la consola muestra la matriz de error, la precisión y la integridad.Como puede ver en la matriz de confusión, hay miles de píxeles que están relacionados con edificios, pero se clasifican de manera diferente, y viceversa. Sin embargo, su participación en el volumen total de datos no es demasiado grande. La precisión e integridad de los datos de prueba excedieron el umbral de 0.8.
Puede pasar más tiempo y realizar varias iteraciones para encontrar el número óptimo de capas ocultas, el número de nodos en cada capa oculta, así como el número de eras para lograr la precisión deseada. Según sea necesario, los índices de teledetección como NDBI o NDWI se pueden usar como características. Al lograr la precisión deseada, use el modelo para predecir el desarrollo basado en nuevos datos y exporte el resultado a GeoTIFF. Para tales tareas, puede usar un modelo similar con cambios menores.
predicted = model.predict(feature2005) predicted = predicted[:,1]
Tenga en cuenta que exportamos GeoTIFF con valores de probabilidad pronosticados, y no con su versión binarizada de umbral. Más adelante en el entorno SIG, podemos establecer el valor umbral de una capa de tipo flotante, como se muestra en la figura a continuación.
Capa acumulada de Hyderabad predicha por el modelo basada en datos multiespectrales.La precisión del modelo ya se ha medido con precisión y recuperación. También puede realizar comprobaciones tradicionales (por ejemplo, utilizando el coeficiente kappa) en una nueva capa prevista. Además de las dificultades antes mencionadas con la clasificación de las imágenes de satélite, otras limitaciones obvias incluyen la imposibilidad de pronósticos basados en imágenes tomadas en diferentes épocas del año y en diferentes regiones, ya que tendrán diferentes firmas espectrales.
El modelo descrito en este artículo tiene la arquitectura más simple para redes neuronales. Se pueden lograr mejores resultados con modelos más complejos, incluidas las redes neuronales convolucionales. La principal ventaja de tal clasificación es su escalabilidad (aplicabilidad) después de entrenar el modelo.
Los datos utilizados y todo el código están
aquí .