Mi nombre es Vyacheslav, soy matemático crónico y durante varios años no he usado ciclos al trabajar con matrices ...
Exactamente desde que descubrí las operaciones vectoriales en NumPy. Quiero presentarles las funciones NumPy que uso con mayor frecuencia para procesar matrices de datos e imágenes. Al final del artículo, le mostraré cómo puede usar el kit de herramientas NumPy para convolucionar imágenes sin iteraciones (= muy rápido).
No te olvides de
import numpy as np
y vamos!
Contenido
¿Qué es numpy?Creación de matrizAcceso a elementos, cortes.La forma de la matriz y su cambio.Reordenamiento y transposición del ejeArray unirseClonación de datosOperaciones matemáticas en elementos de matriz.Multiplicación de matricesAgregadoresEn lugar de una conclusión, un ejemplo¿Qué es numpy?
Esta es una biblioteca de código abierto que una vez se separó del proyecto SciPy. NumPy es el descendiente de Numeric y NumArray. NumPy se basa en la biblioteca LAPAC, que está escrita en Fortran. Una alternativa que no es Python para NumPy es Matlab.
Debido al hecho de que NumPy se basa en Fortran, es una biblioteca rápida. Y debido al hecho de que admite operaciones vectoriales con matrices multidimensionales, es extremadamente conveniente.
Además del caso base (matrices multidimensionales en el caso base) NumPy incluye un conjunto de paquetes para resolver tareas especializadas, por ejemplo:
- numpy.linalg - implementa operaciones de álgebra lineal (una simple multiplicación de vectores y matrices está en la versión básica);
- numpy.random: implementa funciones para trabajar con variables aleatorias;
- numpy.fft: implementa la transformación de Fourier directa e inversa.
Por lo tanto, ¡propongo considerar en detalle solo algunas características de NumPy y ejemplos de su uso, que serán suficientes para que comprenda cuán poderosa es esta herramienta!
<up>Creación de matriz
Hay varias formas de crear una matriz:
- convertir lista a matriz:
A = np.array([[1, 2, 3], [4, 5, 6]]) A Out: array([[1, 2, 3], [4, 5, 6]])
- copie la matriz (se requiere copia y copia profunda !!!):
B = A.copy() B Out: array([[1, 2, 3], [4, 5, 6]])
- crear una matriz cero o una de un tamaño dado:
A = np.zeros((2, 3)) A Out: array([[0., 0., 0.], [0., 0., 0.]])
B = np.ones((3, 2)) B Out: array([[1., 1.], [1., 1.], [1., 1.]])
O tome las dimensiones de una matriz existente:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.zeros_like(A) B Out: array([[0, 0, 0], [0, 0, 0]])
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.ones_like(A) B Out: array([[1, 1, 1], [1, 1, 1]])
- al crear una matriz cuadrada bidimensional, puede convertirla en una matriz de unidad diagonal:
A = np.eye(3) A Out: array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]])
- construya una matriz de números desde Desde (incluido) hasta Hasta (sin incluir) con el paso Paso:
From = 2.5 To = 7 Step = 0.5 A = np.arange(From, To, Step) A Out: array([2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5])
Por defecto, desde = 0, paso = 1, por lo que una variante con un parámetro se interpreta como Para:
A = np.arange(5) A Out: array([0, 1, 2, 3, 4])
O con dos, como From y To:
A = np.arange(10, 15) A Out: array([10, 11, 12, 13, 14])
Tenga en cuenta que en el método No. 3, las dimensiones de la matriz se pasaron como
un parámetro (una tupla de tamaños). El segundo parámetro en los métodos No. 3 y No. 4, puede especificar el tipo deseado de elementos de matriz:
A = np.zeros((2, 3), 'int') A Out: array([[0, 0, 0], [0, 0, 0]])
B = np.ones((3, 2), 'complex') B Out: array([[1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j]])
Usando el método astype, puede convertir la matriz a un tipo diferente. El tipo deseado se indica como un parámetro:
A = np.ones((3, 2)) B = A.astype('str') B Out: array([['1.0', '1.0'], ['1.0', '1.0'], ['1.0', '1.0']], dtype='<U32')
Todos los tipos disponibles se pueden encontrar en el diccionario de sctypes:
np.sctypes Out: {'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64], 'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64], 'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128], 'complex': [numpy.complex64, numpy.complex128, numpy.complex256], 'others': [bool, object, bytes, str, numpy.void]}
<up>Acceso a elementos, cortes.
El acceso a los elementos de la matriz se realiza mediante índices enteros, la cuenta regresiva comienza desde 0:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, 1] Out: 5
Si imagina una matriz multidimensional como un sistema de matrices unidimensionales anidadas (una matriz lineal, cuyos elementos pueden ser matrices lineales), resulta obvio que puede acceder a las submatrices utilizando un conjunto incompleto de índices:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1] Out: array([4, 5, 6])
Dado este paradigma, podemos reescribir el ejemplo de acceso a un elemento:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1][1] Out: 5
Cuando se utiliza un conjunto incompleto de índices, los índices que faltan se reemplazan implícitamente por una lista de todos los índices posibles a lo largo del eje correspondiente. Puede hacer esto explícitamente configurando ":". El ejemplo anterior con un índice puede reescribirse de la siguiente manera:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, :] Out: array([4, 5, 6])
Puede omitir un índice a lo largo de cualquier eje o ejes; si el eje es seguido por ejes con indexación, entonces ":" debe:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[:, 1] Out: array([2, 5])
Los índices pueden tomar valores enteros negativos. En este caso, el recuento es desde el final de la matriz:
A = np.arange(5) print(A) A[-1] Out: [0 1 2 3 4] 4
Puede usar no índices individuales, sino listas de índices a lo largo de cada eje:
A = np.arange(5) print(A) A[[0, 1, -1]] Out: [0 1 2 3 4] array([0, 1, 4])
O rangos de índice en forma de "De: A: Paso". Este diseño se llama una rebanada. Todos los elementos se seleccionan de acuerdo con la lista de índices que comienzan desde el índice Desde inclusive, hasta el índice Hasta, no
incluido en el paso Paso:
A = np.arange(5) print(A) A[0:4:2] Out: [0 1 2 3 4] array([0, 2])
El paso del índice tiene un valor predeterminado de 1 y se puede omitir:
A = np.arange(5) print(A) A[0:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
Los valores Desde y Hasta también tienen valores predeterminados: 0 y el tamaño de la matriz a lo largo del eje de índice, respectivamente:
A = np.arange(5) print(A) A[:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
A = np.arange(5) print(A) A[-3:] Out: [0 1 2 3 4] array([2, 3, 4])
Si desea usar From y To por defecto (todos los índices en este eje) y el paso es diferente de 1, entonces necesita usar dos pares de dos puntos para que el intérprete pueda identificar un solo parámetro como Step. El siguiente código "expande" la matriz a lo largo del segundo eje, pero no cambia a lo largo del primero:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
Ahora hagámoslo
print(A) B[0, 0] = 0 print(A) Out: [[1 2 3] [4 5 6]] [[1 2 0] [4 5 6]]
Como puede ver, a través de B cambiamos los datos en A. Por eso es importante usar copias en tareas reales. El ejemplo anterior debería verse así:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.copy()[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
NumPy también proporciona la capacidad de acceder a múltiples elementos de matriz a través de una matriz de índice booleano. La matriz de índice debe coincidir con la forma de la indexada.
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] Out: array([3, 4, 6])
Como puede ver, dicha construcción devuelve una matriz plana que consta de elementos de la matriz indexada que corresponden a índices verdaderos. Sin embargo, si usamos dicho acceso a los elementos de la matriz para cambiar sus valores, entonces se preservará la forma de la matriz:
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] = 0 print(A) Out: [[1 2 0] [0 5 0]]
Las operaciones lógicas logical_and, logical_or y logical_not se definen sobre la indexación de matrices booleanas y realizan operaciones lógicas AND, OR y NOT por elementos:
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) B = A.copy() C = A.copy() D = A.copy() B[np.logical_and(I1, I2)] = 0 C[np.logical_or(I1, I2)] = 0 D[np.logical_not(I1)] = 0 print('B\n', B) print('\nC\n', C) print('\nD\n', D) Out: B [[1 2 3] [4 5 0]] C [[1 0 0] [0 5 0]] D [[0 0 3] [4 0 6]]
logical_and y logical_or toman 2 operandos, logical_not toma uno. Puede usar los operadores &, | y ~ para ejecutar AND, OR y NOT, respectivamente, con cualquier número de operandos:
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) A[I1 & (I1 | ~ I2)] = 0 print(A) Out: [[1 2 0] [0 5 0]]
Lo que equivale a usar solo I1.
Es posible obtener una matriz lógica de indexación correspondiente en forma a una matriz de valores escribiendo una condición lógica con el nombre de la matriz como un operando. El valor booleano del índice se calculará como la verdad de la expresión para el elemento de matriz correspondiente.
Encuentre una matriz de indexación de elementos I que sea mayor que 3, y los elementos con valores menores que 2 y mayores que 4 se restablecerán a cero:
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A before\n', A) I = A > 3 print('I\n', I) A[np.logical_or(A < 2, A > 4)] = 0 print('A after\n', A) Out: A before [[1 2 3] [4 5 6]] I [[False False False] [ True True True]] A after [[0 2 3] [4 0 0]]
<up>La forma de la matriz y su cambio.
Una matriz multidimensional puede representarse como una matriz unidimensional de longitud máxima, cortada en fragmentos a lo largo del último eje y colocada en capas a lo largo de los ejes, comenzando por el último.
Para mayor claridad, considere un ejemplo:
A = np.arange(24) B = A.reshape(4, 6) C = A.reshape(4, 3, 2) print('B\n', B) print('\nC\n', C) Out: B [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23]] C [[[ 0 1] [ 2 3] [ 4 5]] [[ 6 7] [ 8 9] [10 11]] [[12 13] [14 15] [16 17]] [[18 19] [20 21] [22 23]]]
En este ejemplo, formamos 2 nuevas matrices a partir de una matriz unidimensional con una longitud de 24 elementos. Matriz B, tamaño 4 por 6. Si observa el orden de los valores, puede ver que a lo largo de la segunda dimensión hay cadenas de valores secuenciales.
En la matriz C, 4 por 3 por 2, los valores continuos corren a lo largo del último eje. A lo largo del segundo eje hay bloques en serie, cuya combinación daría como resultado una fila a lo largo del segundo eje de la matriz B.
Y dado que no hicimos copias, queda claro que estas son formas diferentes de representación de la misma matriz de datos. Por lo tanto, puede cambiar fácil y rápidamente la forma de la matriz sin cambiar los datos en sí.
Para averiguar la dimensión de la matriz (número de ejes), puede usar el campo ndim (número) y para determinar el tamaño a lo largo de cada eje - forma (tupla). La dimensión también se puede reconocer por la longitud de la forma. Para averiguar el número total de elementos en una matriz, puede usar el valor de tamaño:
A = np.arange(24) C = A.reshape(4, 3, 2) print(C.ndim, C.shape, len(C.shape), A.size) Out: 3 (4, 3, 2) 3 24
¡Tenga en cuenta que ndim y shape son atributos, no métodos!
Para ver la matriz unidimensional, puede usar la función de desvanecimiento:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.ravel() Out: array([1, 2, 3, 4, 5, 6])
Para cambiar el tamaño a lo largo de los ejes o la dimensión, use el método de remodelación:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 2) Out: array([[1, 2], [3, 4], [5, 6]])
Es importante que se conserve el número de elementos. De lo contrario, se producirá un error:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 3) Out: ValueError Traceback (most recent call last) <ipython-input-73-d204e18427d9> in <module> 1 A = np.array([[1, 2, 3], [4, 5, 6]]) ----> 2 A.reshape(3, 3) ValueError: cannot reshape array of size 6 into shape (3,3)
Dado que el número de elementos es constante, el tamaño a lo largo de cualquier eje cuando se reforma puede calcularse a partir de los valores de longitud a lo largo de otros ejes. El tamaño a lo largo de un eje se puede designar -1 y luego se calculará automáticamente:
A = np.arange(24) B = A.reshape(4, -1) C = A.reshape(4, -1, 2) print(B.shape, C.shape) Out: (4, 6) (4, 3, 2)
Puede usar remodelar en lugar de deshilachar:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.reshape(-1) print(B.shape) Out: (6,)
Considere la aplicación práctica de algunas de las funciones para el procesamiento de imágenes. Como objeto de investigación utilizaremos una fotografía:
Intentemos descargarlo y visualizarlo usando Python. Para esto necesitamos OpenCV y Matplotlib:
import cv2 from matplotlib import pyplot as plt I = cv2.imread('sarajevo.jpg')[:, :, ::-1] plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I) plt.show()
El resultado será así:
Presta atención a la barra de descarga:
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] print(I.shape) Out: (1280, 1920, 3)
OpenCV funciona con imágenes en formato BGR, y estamos familiarizados con RGB. Cambiamos el orden de los bytes a lo largo del eje de color sin acceder a las funciones de OpenCV usando la construcción
"[:,:, :: :: 1]".
Reduzca la imagen 2 veces en cada eje. Nuestra imagen tiene dimensiones uniformes a lo largo de los ejes, respectivamente, se puede reducir sin interpolación:
I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) print(I_.shape) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_[:, 0, :, 0]) plt.show()
Cambiando la forma de la matriz, obtuvimos 2 ejes nuevos, 2 valores en cada uno, corresponden a cuadros compuestos de filas y columnas impares y pares de la imagen original.
La mala calidad se debe al uso de Matplotlib, porque allí puede ver las dimensiones axiales. De hecho, la calidad de la miniatura es:
<up>Reordenamiento y transposición del eje
Además de cambiar la forma de la matriz con el mismo orden de unidades de datos, a menudo es necesario cambiar el orden de los ejes, lo que naturalmente implicará la permutación de los bloques de datos.
Un ejemplo de tal transformación es la transposición de una matriz: intercambio de filas y columnas.
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A\n', A) print('\nA data\n', A.ravel()) B = AT print('\nB\n', B) print('\nB data\n', B.ravel()) Out: A [[1 2 3] [4 5 6]] A data [1 2 3 4 5 6] B [[1 4] [2 5] [3 6]] B data [1 4 2 5 3 6]
En este ejemplo, la construcción AT se utilizó para transponer la matriz A. El operador de transposición invierte el orden del eje. Considere otro ejemplo con tres ejes:
C = np.arange(24).reshape(4, -1, 2) print(C.shape, np.transpose(C).shape) print() print(C[0]) print() print(CT[:, :, 0]) Out: [[0 1] [2 3] [4 5]] [[0 2 4] [1 3 5]]
Esta entrada corta tiene una contraparte más larga: np.transpose (A). Esta es una herramienta más versátil para reemplazar el orden de los ejes. El segundo parámetro le permite especificar una tupla de números de eje de la matriz fuente, que determina el orden de su posición en la matriz resultante.
Por ejemplo, reorganice los dos primeros ejes de la imagen. La imagen debería voltearse, pero dejar el eje de color sin cambios:
I_ = np.transpose(I, (1, 0, 2)) plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_) plt.show()
Para este ejemplo, podría usarse otra herramienta swapaxes. Este método intercambia los dos ejes especificados en los parámetros. El ejemplo anterior podría implementarse así:
I_ = np.swapaxes(I, 0, 1)
<up>Array unirse
Las matrices fusionadas deben tener el mismo número de ejes. Las matrices se pueden combinar con la formación de un nuevo eje, o a lo largo de uno existente.
Para combinar con la formación de un nuevo eje, las matrices originales deben tener las mismas dimensiones en todos los ejes:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) print(D.shape) D Out: (3, 2, 4) array([[[1, 2, 3, 4], [5, 6, 7, 8]], [[5, 6, 7, 8], [1, 2, 3, 4]], [[4, 3, 2, 1], [8, 7, 6, 5]]])
Como puede ver en el ejemplo, las matrices de operandos se convirtieron en submatrices del nuevo objeto y se alinearon a lo largo del nuevo eje, que es el primero en orden.
Para combinar matrices a lo largo de un eje existente, deben tener el mismo tamaño en todos los ejes, excepto el seleccionado para unir, y pueden tener tamaños arbitrarios a lo largo de él:
A = np.ones((2, 1, 2)) B = np.zeros((2, 3, 2)) C = np.concatenate((A, B), 1) print(C.shape) C Out: (2, 4, 2) array([[[1., 1.], [0., 0.], [0., 0.], [0., 0.]], [[1., 1.], [0., 0.], [0., 0.], [0., 0.]]])
Para combinar a lo largo del primer o segundo eje, puede usar los métodos vstack y hstack, respectivamente. Mostramos esto con un ejemplo de imágenes. vstack combina imágenes del mismo ancho en altura, y hsstack combina las mismas imágenes de altura en un ancho:
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) Ih = np.hstack((I_[:, 0, :, 0], I_[:, 0, :, 1])) Iv = np.vstack((I_[:, 0, :, 0], I_[:, 1, :, 0])) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Ih) plt.show() plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Iv) plt.show()
Tenga en cuenta que en todos los ejemplos de esta sección, las matrices unidas se pasan por un parámetro (tupla). El número de operandos puede ser cualquiera, pero no necesariamente solo 2.
También preste atención a lo que le sucede a la memoria al combinar matrices:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) D[0, 0, 0] = 0 print(A) Out: [[1 2 3 4] [5 6 7 8]]
Como se crea un nuevo objeto, los datos que contiene se copian de las matrices originales, por lo que los cambios en los nuevos datos no afectan al original.
<up>Clonación de datos
El operador np.repeat (A, n) devolverá una matriz unidimensional con elementos de la matriz A, cada uno de los cuales se repetirá n veces.
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) print(np.repeat(A, 2)) Out: [1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8]
Después de esta conversión, puede reconstruir la geometría de la matriz y recopilar datos duplicados en un eje:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1) print(B) Out: [[[1 1] [2 2] [3 3] [4 4]] [[5 5] [6 6] [7 7] [8 8]]]
Esta opción difiere de combinar la matriz con el operador de la pila solo en la posición del eje a lo largo de la cual se encuentran los mismos datos. En el ejemplo anterior, este es el último eje, si usa stack, el primero:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.stack((A, A)) print(B) Out: [[[1 2 3 4] [5 6 7 8]] [[1 2 3 4] [5 6 7 8]]]
No importa cómo se clonen los datos, el siguiente paso es mover el eje a lo largo del cual se ubican los mismos valores en cualquier posición con el sistema de ejes:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.transpose(np.stack((A, A)), (1, 0, 2)) C = np.transpose(np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1), (0, 2, 1)) print('B\n', B) print('\nC\n', C) Out: B [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]] C [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]]
Si queremos "estirar" cualquier eje usando la repetición de elementos, entonces el eje con los mismos valores debe colocarse
después del expandible (usando transposición), y luego combinar estos dos ejes (usando reformar). Considere un ejemplo con estirar una imagen a lo largo de un eje vertical duplicando filas:
I0 = cv2.imread('sarajevo.jpg')[:, :, ::-1]
<up>Operaciones matemáticas en elementos de matriz.
Si A y B son matrices del mismo tamaño, se pueden sumar, multiplicar, restar, dividir y elevar a una potencia. Estas operaciones se realizan
elemento por elemento , la matriz resultante coincidirá en geometría con las matrices originales, y cada uno de sus elementos será el resultado de la operación correspondiente en un par de elementos de las matrices originales:
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([[1., -2., -3.], [7., 8., 9.], [4., 5., 6.], ]) C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[ 0. 0. 0.] [11. 13. 15.] [11. 13. 15.]] - [[-2. 4. 6.] [-3. -3. -3.] [ 3. 3. 3.]] * [[-1. -4. -9.] [28. 40. 54.] [28. 40. 54.]] / [[-1. -1. -1. ] [ 0.57142857 0.625 0.66666667] [ 1.75 1.6 1.5 ]] ** [[-1.0000000e+00 2.5000000e-01 3.7037037e-02] [ 1.6384000e+04 3.9062500e+05 1.0077696e+07] [ 2.4010000e+03 3.2768000e+04 5.3144100e+05]]
Puede realizar cualquier operación de lo anterior en la matriz y el número. En este caso, la operación también se realizará en cada uno de los elementos de la matriz:
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = -2. C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-3. 0. 1.] [ 2. 3. 4.] [ 5. 6. 7.]] - [[ 1. 4. 5.] [ 6. 7. 8.] [ 9. 10. 11.]] * [[ 2. -4. -6.] [ -8. -10. -12.] [-14. -16. -18.]] / [[ 0.5 -1. -1.5] [-2. -2.5 -3. ] [-3.5 -4. -4.5]] ** [[1. 0.25 0.11111111] [0.0625 0.04 0.02777778] [0.02040816 0.015625 0.01234568]]
Dado que una matriz multidimensional puede considerarse como una matriz plana (primer eje), cuyos elementos son matrices (otros ejes), es posible realizar las operaciones consideradas en las matrices A y B en el caso de que la geometría de B coincida con la geometría de las submatrices de A con un valor fijo a lo largo del primer eje . En otras palabras, con el mismo número de ejes y tamaños A [i] y B. En este caso, cada una de las matrices A [i] y B serán operandos para operaciones definidas en matrices.
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = AT + B D = AT - B E = AT * B F = AT / B G = AT ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 2.8 5.7] [ 0.9 3.8 6.7] [ 1.9 4.8 7.7]] - [[ 2.1 5.2 8.3] [ 3.1 6.2 9.3] [ 4.1 7.2 10.3]] * [[ -1.1 -4.8 -9.1] [ -2.2 -6. -10.4] [ -3.3 -7.2 -11.7]] / [[-0.90909091 -3.33333333 -5.38461538] [-1.81818182 -4.16666667 -6.15384615] [-2.72727273 -5. -6.92307692]] ** [[1. 0.18946457 0.07968426] [0.4665165 0.14495593 0.06698584] [0.29865282 0.11647119 0.05747576]]
En este ejemplo, la matriz B está sujeta a la operación con cada fila de la matriz A. Si necesita multiplicar / dividir / sumar / restar / elevar el grado de submatrices a lo largo de otro eje, debe usar la transposición para colocar el eje deseado en su primer lugar, y luego devolverlo a su lugar. Considere el ejemplo anterior, pero con la multiplicación por el vector B de las columnas de la matriz A:
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = (AT + B).T D = (AT - B).T E = (AT * B).T F = (AT / B).T G = (AT ** B).T print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 0.9 1.9] [ 2.8 3.8 4.8] [ 5.7 6.7 7.7]] - [[ 2.1 3.1 4.1] [ 5.2 6.2 7.2] [ 8.3 9.3 10.3]] * [[ -1.1 -2.2 -3.3] [ -4.8 -6. -7.2] [ -9.1 -10.4 -11.7]] / [[-0.90909091 -1.81818182 -2.72727273] [-3.33333333 -4.16666667 -5. ] [-5.38461538 -6.15384615 -6.92307692]] ** [[1. 0.4665165 0.29865282] [0.18946457 0.14495593 0.11647119] [0.07968426 0.06698584 0.05747576]]
Para funciones más complejas (por ejemplo, trigonométrica, exponente, logaritmo, conversión entre grados y radianes, módulo, raíz cuadrada, etc.), NumPy tiene una implementación. Considere el ejemplo de exponencial y logaritmo: A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.exp(A) C = np.log(B) print('A', A, '\n') print('B', B, '\n') print('C', C, '\n') Out: A [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] B [[2.71828183e+00 7.38905610e+00 2.00855369e+01] [5.45981500e+01 1.48413159e+02 4.03428793e+02] [1.09663316e+03 2.98095799e+03 8.10308393e+03]] C [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]]
Una lista completa de operaciones matemáticas en NumPy se puede encontrar aquí .<up>Multiplicación de matrices
La operación anterior del producto de matrices se realiza por elementos. Y si necesita realizar operaciones de acuerdo con las reglas del álgebra lineal en matrices como en tensores, puede usar el método de punto (A, B). Dependiendo del tipo de operandos, la función realizará:- si los argumentos son escalares (números), se realizará la multiplicación;
- si los argumentos son un vector (matriz unidimensional) y un escalar, entonces la matriz se multiplicará por un número;
- si los argumentos son vectoriales, se realizará una multiplicación escalar (la suma de los productos de elementos sabios);
- si los argumentos son tensoriales (matriz multidimensional) y escalares, entonces el vector se multiplicará por un número;
- si los argumentos del tensor, entonces se ejecutará el producto de los tensores a lo largo del último eje del primer argumento y el penúltimo segundo;
- si los argumentos son matrices, entonces se ejecuta el producto de las matrices (este es un caso especial del producto de los tensores);
- si los argumentos son matriz y vector, entonces se ejecutará el producto de la matriz y el vector (este también es un caso especial del producto de los tensores).
Para realizar las operaciones, los tamaños correspondientes deben coincidir: para vectores de longitud, para tensores, las longitudes a lo largo de los ejes a lo largo de los cuales se sumarán los productos por elementos.Considere ejemplos con escalares y vectores:
Con los tensores, solo veremos cómo la geometría de la matriz resultante cambia de tamaño:
Para realizar un producto tensor con otros ejes, en lugar de los definidos para punto, puede usar tensordot con un eje explícito: A = np.ones((1, 3, 7, 4)) B = np.ones((5, 7, 6, 7, 8)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.tensordot(A, B, [2, 1]).shape, '\n\n') Out: A: (1, 3, 7, 4) B: (5, 7, 6, 7, 8) result: (1, 3, 4, 5, 6, 7, 8)
Hemos indicado explícitamente que usamos el tercer eje de la primera matriz y el segundo - del segundo (los tamaños a lo largo de estos ejes deben coincidir).<up>Agregadores
Los agregadores son métodos NumPy que le permiten reemplazar datos con características integrales a lo largo de algunos ejes. Por ejemplo, puede calcular el valor promedio, máximo, mínimo, variación u otra característica a lo largo de cualquier eje o ejes y formar una nueva matriz a partir de estos datos. La forma de la nueva matriz contendrá todos los ejes de la matriz original, excepto aquellos a lo largo de los cuales se contó el agregador.Por ejemplo, formaremos una matriz con valores aleatorios. Luego encontramos el valor mínimo, máximo y promedio en sus columnas: A = np.random.rand(4, 5) print('A\n', A, '\n') print('min\n', np.min(A, 0), '\n') print('max\n', np.max(A, 0), '\n') print('mean\n', np.mean(A, 0), '\n') print('average\n', np.average(A, 0), '\n') Out: A [[0.58481838 0.32381665 0.53849901 0.32401355 0.05442121] [0.34301843 0.38620863 0.52689694 0.93233065 0.73474868] [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] [0.74758173 0.73529492 0.58517879 0.11785686 0.81204847]] min [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] max [0.74758173 0.73529492 0.58517879 0.93233065 0.81204847] mean [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039] average [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039]
Con este uso, la media y la media parecen sinónimos. Pero estas funciones tienen un conjunto diferente de parámetros adicionales. Existen diferentes posibilidades para enmascarar y ponderar datos promediados.Puede calcular las características integrales en varios ejes: A = np.ones((10, 4, 5)) print('sum\n', np.sum(A, (0, 2)), '\n') print('min\n', np.min(A, (0, 2)), '\n') print('max\n', np.max(A, (0, 2)), '\n') print('mean\n', np.mean(A, (0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
En este ejemplo, se considera otra suma característica integral: la suma.La lista de agregadores se ve así:- sum: sum y nansum: una variante que se gestiona correctamente con nan;
- trabajo: prod y nanprod;
- promedio y expectativa: promedio y promedio (nanmedio),
no hay un promedio nano ; - mediana: mediana y nanmedian;
- percentil: percentil y nanpercentil;
- variación: var y nanvar;
- desviación estándar (raíz cuadrada de variación): std y nanstd;
- : min nanmin;
- : max nanmax;
- , : argmin nanargmin;
- , : argmax nanargmax.
En el caso de utilizar argmin y argmax (respectivamente, nanargmin y nanargmax), debe especificar un eje a lo largo del cual se considerará la característica.Si no especifica un eje, por defecto, todas las características consideradas se consideran en toda la matriz. En este caso, argmin y argmax también funcionarán correctamente y encontrarán el índice del elemento máximo o mínimo, como si todos los datos de la matriz se extendieran a lo largo del mismo eje con el comando ravel ().También se debe tener en cuenta que los métodos de agregación se definen no solo como métodos del módulo NumPy, sino también para las matrices mismas: la entrada np.aggregator (A, ejes) es equivalente a la entrada A.aggregator (ejes), donde agregador significa una de las funciones consideradas anteriormente, y por ejes - índices de eje. A = np.ones((10, 4, 5)) print('sum\n', A.sum((0, 2)), '\n') print('min\n', A.min((0, 2)), '\n') print('max\n', A.max((0, 2)), '\n') print('mean\n', A.mean((0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
<up>En lugar de una conclusión, un ejemplo
Construyamos un algoritmo para el filtrado lineal de imágenes de paso bajo.Para comenzar, suba una imagen ruidosa.
Considere un fragmento de la imagen para ver el ruido:
filtraremos la imagen usando un filtro gaussiano. Pero en lugar de hacer la convolución directamente (con iteración), aplicamos el promedio ponderado de los cortes de imagen desplazados uno respecto al otro: def smooth(I): J = I.copy() J[1:-1] = (J[1:-1] // 2 + J[:-2] // 4 + J[2:] // 4) J[:, 1:-1] = (J[:, 1:-1] // 2 + J[:, :-2] // 4 + J[:, 2:] // 4) return J
Aplicamos esta función a nuestra imagen una, dos y tres veces: I_noise = cv2.imread('sarajevo_noise.jpg') I_denoise_1 = smooth(I_noise) I_denoise_2 = smooth(I_denoise_1) I_denoise_3 = smooth(I_denoise_2) cv2.imwrite('sarajevo_denoise_1.jpg', I_denoise_1) cv2.imwrite('sarajevo_denoise_2.jpg', I_denoise_2) cv2.imwrite('sarajevo_denoise_3.jpg', I_denoise_3)
Obtenemos los siguientes resultados:
con un solo uso del filtro;
con doble;
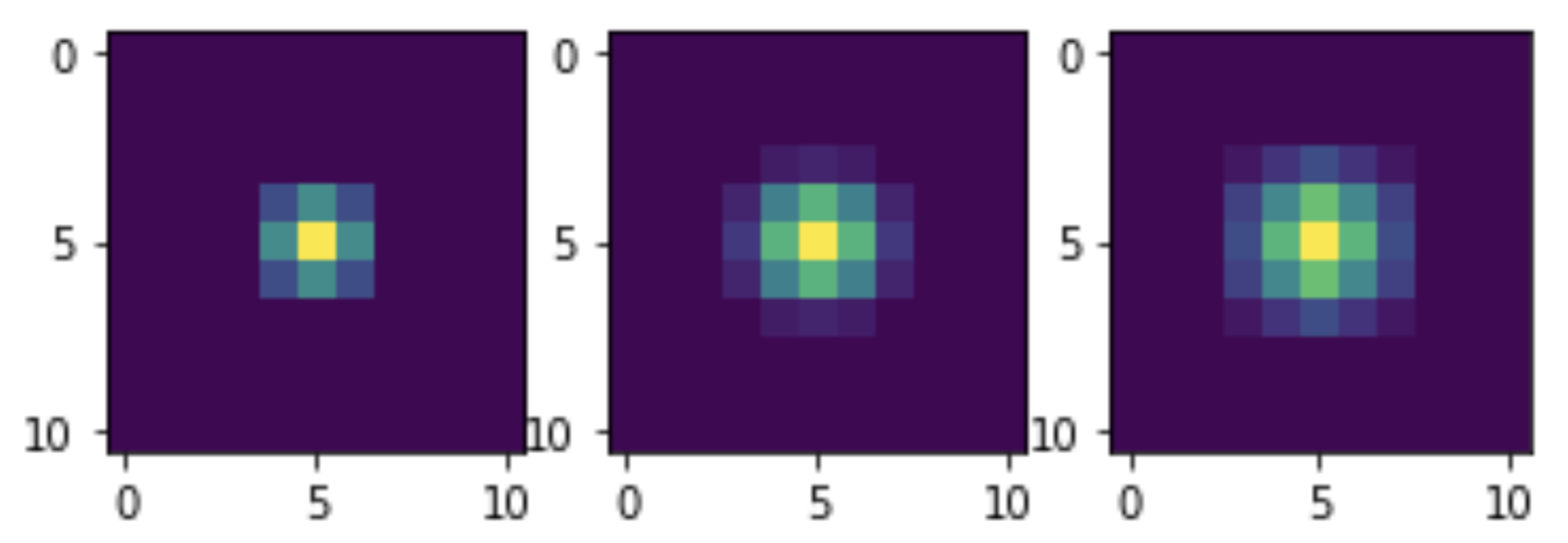
A las tres veces.Se puede ver que con un aumento en el número de pasadas de filtro, el nivel de ruido disminuye. Pero esto también reduce la claridad de la imagen. Este es un problema conocido con los filtros lineales. Pero nuestro método de eliminación de imágenes no pretende ser óptimo: esto es solo una demostración de las capacidades de NumPy para implementar convolución sin iteraciones.Ahora veamos la convolución con que núcleos nuestro filtrado es equivalente. Para hacer esto, someteremos un impulso de una sola unidad a transformaciones y visualizaciones similares. De hecho, el impulso no será único, sino que tendrá una amplitud igual a 255, ya que la mezcla en sí está optimizada para datos enteros. Pero esto no interfiere con la evaluación de la apariencia general de los núcleos: M = np.zeros((11, 11)) M[5, 5] = 255 M1 = smooth(M) M2 = smooth(M1) M3 = smooth(M2) plt.subplot(1, 3, 1) plt.imshow(M1) plt.subplot(1, 3, 2) plt.imshow(M2) plt.subplot(1, 3, 3) plt.imshow(M3) plt.show()
Consideramos un conjunto de características NumPy lejos de ser completo, ¡espero que esto sea suficiente para demostrar todo el poder y la belleza de esta herramienta!<up>