Recientemente, se subió a arXiv.org [arXiv: 1909.04240] un artículo con el título no tan intrigante, "
La reparameterización neuronal mejora la optimización estructural ". Sin embargo, resultó que los autores, de hecho, idearon y describieron un método muy trivial de usar una red neuronal para obtener una solución al problema de la optimización estructural / topológica de los modelos físicos (aunque los propios autores dicen que el método es más universal). El enfoque es muy curioso, productivo y parece ser completamente nuevo (sin embargo, no puedo responder por esto último, pero ni los autores del trabajo, ni la comunidad ODS, ni pude recordar análogos), por lo que puede ser útil saber para aquellos interesados en usar redes neuronales, además de resolver varios problemas de optimización.
De que estas hablando ¿Cuál es la tarea de la optimización topológica?
Solo imagine lo que necesita, por ejemplo, para diseñar un hilo de un puente, un edificio de varios pisos, un ala de avión, una pala de turbina, o lo que sea. Por lo general, esto se resuelve encontrando un especialista, por ejemplo, un arquitecto que, utilizando su conocimiento de matan, sopromat, el área objetivo, así como su experiencia, intuición, diseños de prueba, etc. etc. crearía el proyecto deseado. Es importante aquí que este proyecto recibido sea bueno solo para lo mejor de este especialista. Y esto, obviamente, no siempre es suficiente. Por lo tanto, cuando las computadoras se volvieron lo suficientemente potentes, comenzamos a tratar de trasladar esas tareas a ellas. Porque
es obvio lo que una computadora puede guardar en la memoria y cortocircuito ... ¿por qué no?
Dichas tareas se denominan "problemas de optimización estructural", es decir generando un diseño óptimo de estructuras mecánicas de carga [1]. Una subsección de problemas de optimización estructural son
los problemas de optimización topológica (de hecho, el trabajo en cuestión se centra específicamente en ellos, pero este no es el punto, y más sobre eso más adelante). Un problema típico de optimización topológica se parece a esto: para un concepto dado (puente, casa, etc.) en el espacio en dos o tres dimensiones, con limitaciones específicas en forma de materiales, tecnologías y otros requisitos, con algunas cargas externas, debe diseñar Una estructura óptima que sostendrá cargas y satisfará restricciones.
- "Diseñar" esencialmente significa encontrar / describir un subespacio del espacio fuente que debe llenarse con material de construcción.
- La óptima puede expresarse, por ejemplo, en la forma de un requisito para minimizar el peso total de la estructura bajo restricciones en la forma de las tensiones máximas permitidas en el material y los posibles desplazamientos a las cargas dadas.
Para resolver este problema en una computadora, el espacio de la solución objetivo se muestrea en un conjunto de elementos finitos (píxeles para 2D y voxels para 3D) y luego, usando algún algoritmo, la computadora decide si llenar este elemento individual con material o dejarlo vacío.

(Imagen de "Desarrollos en topología y optimización de formas", Chau Hoai Le, 2010)
Entonces, a partir de la declaración del problema, está claro que su solución es una astilla bastante grande para los científicos. Puedo ofrecer a aquellos que desean algunos detalles, por ejemplo, mirar uno muy antiguo (2010, que todavía es mucho para un campo en desarrollo activo), pero una disertación Chau Hoai Le bastante detallada y fácil de google titulada "Desarrollos en topología y optimización de formas" [2], desde donde Robé las fotos superior e inferior.
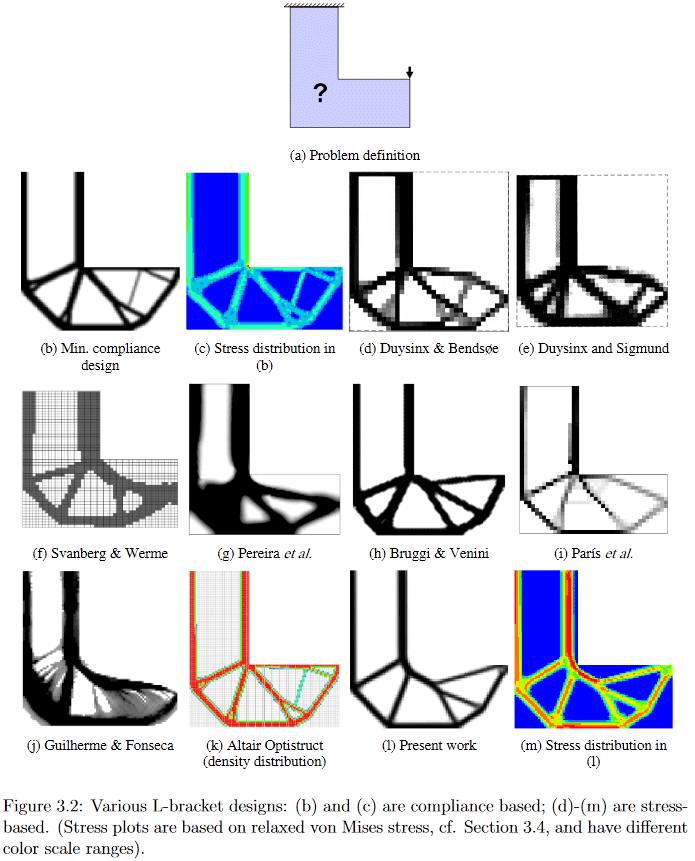
(Imagen de "Desarrollos en topología y optimización de formas", Chau Hoai Le, 2010)
Como ejemplo, en esta imagen puede ver claramente cómo algoritmos muy diferentes generan una solución al problema de diseño aparentemente simple de la suspensión en forma de L.
Entonces, ahora volviendo al trabajo en cuestión.
Los autores sugirieron ingeniosamente resolver tales problemas de optimización generando una solución candidata mediante una red neuronal y la evolución posterior de la solución mediante métodos de descenso de gradiente con respecto a la función de cumplimiento objetivo. El cumplimiento de la estructura resultante se estima utilizando un modelo físico diferenciable, que, de hecho, permite el uso del descenso de gradiente. Según ellos (los autores publicaron los
códigos fuente de [5]), esto da el mismo resultado que los mejores algoritmos tradicionales para problemas simples, o el mejor de estos algoritmos utilizados como líneas de base, para los complejos.
Método
A continuación, trataré de describir qué y cómo se propusieron exactamente los autores, pero inmediatamente advierto que no estoy garantizando el 100% de corrección, porque además de mi erudición extremadamente oxidada en el campo, debo agregar, además de la brevedad extremadamente exigua de la descripción, alguna "inmadurez" general del artículo, que, a juzgar por la presencia de dos ediciones en 4 días, está en proceso de finalización (
agregado: por el momento, creo que, al menos, básicamente, todo se describe correctamente).
Los autores, en general, siguen el enfoque para resolver tales problemas de optimización, llamado "método SIMP modificado", y lo describen con suficiente detalle en [3] "Optimización de topología eficiente en MATLAB utilizando 88 líneas de código". La preimpresión de este trabajo y el código asociado se pueden encontrar en
http://www.topopt.mek.dtu.dk/Apps-and-software/Efficient-topology-optimization-in-MATLAB . Este trabajo a menudo se usa para comenzar a enseñar a los estudiantes sobre problemas de optimización topológica, por lo tanto, para comprenderlo mejor, se recomienda familiarizarse con él.
En "SIMP modificado", la solución se optimiza directamente modificando los píxeles de la imagen de las densidades físicas. Los autores del artículo no propusieron modificar la imagen directamente (aunque dicho algoritmo, con otras cosas iguales, era uno de control), sino cambiar los parámetros y la entrada de la red neuronal convolucional que genera una imagen de densidades físicas. Así es como se ve todo el método globalmente:

(Imagen de la publicación en cuestión)
Paso 1, generando un candidato
Una red neuronal (en lo sucesivo denominada NS) que utiliza el vector de entrada primaria aleatoria _beta (es, como el peso de la red, es un parámetro entrenado), genera (alguna) imagen de la solución (funciona con 2D, pero creo que en 3D también se puede distribuir ) La parte de muestreo superior de la conocida arquitectura U-Net se utiliza como generador de NS.
Paso 2, aplicando restricciones y convirtiendo a un candidato a un marco de modelo físico
Los valores de píxeles se convierten en densidades físicas en dos pasos:
- Primero, en un paso, se resuelve el problema de la normalización de los valores no normalizados de los píxeles generados (el NS está diseñado de modo que genera los llamados logits - valores en el rango (-inf, + inf)) y aplica restricciones en la cantidad total de la solución resultante. Para esto, se aplica un elemento sigmoide a la imagen, el argumento del cual se desplaza por una constante dependiendo de la imagen que se está transformando y el volumen de la solución deseada (el valor de esta constante de polarización se selecciona mediante búsqueda binaria para que el volumen total de las densidades así obtenidas sea igual a un cierto volumen predeterminado V0). Un análisis detallado de esta etapa, ver el comentario );
- Además, la imagen normalizada resultante de las densidades de la estructura es procesada por el llamado un filtro de densidad con un radio de 2. En términos más conocidos, este filtro no es más que un promedio ponderado normal de puntos vecinos en la imagen. Los pesos en este filtro (núcleo del filtro) se pueden representar como los valores de las alturas de los puntos ubicados en la superficie de un cono regular que se encuentra en el plano para que su vértice esté en el punto actual, por lo tanto, los autores lo llaman filtro de cono (en más detalle sobre este tema consulte la descripción del filtro de densidad en el capítulo 2.3 Filtrado de [3]).
En resumen, la esencia de todo el paso 2 es que la salida no normalizada de un NS completamente ordinario se convierte en un marco del modelo físico ligeramente normalizado y correctamente suavizado (un conjunto de densidades físicas de elementos), al que ya se han aplicado las restricciones a priori necesarias (esta es la cantidad de material utilizado).
Paso 3, evaluación del modelo físico del marco resultante
El marco resultante se ejecuta a través de un motor físico diferenciable para obtener el vector (¿/ tensor?) Del desplazamiento estructural bajo carga (incluida la gravedad) U. La clave aquí es la diferenciabilidad del motor, que nos permite obtener gradientes (recuerdo que el gradiente de la función es generalmente tensor compuesto de derivadas parciales de una función con respecto a todos sus argumentos. El gradiente muestra la dirección y la tasa de cambio de la función en el punto actual, por lo tanto, al conocerlo, puede "torcer" los argumentos para que el cambio deseado ocurra con la función - disminuyó o aumentó). Un motor físico tan diferenciable no necesita ser escrito desde cero: han existido durante mucho tiempo y son bien conocidos. Los autores solo necesitaban hacer su emparejamiento con paquetes de cálculo de redes neuronales, como TensorFlow / PyTorch.
Paso 4, calcular el valor de la función objetivo para la estructura alámbrica / candidato
Se calcula la función objetivo escalar c (x) a minimizar, que describe el cumplimiento (es el inverso de la rigidez) del marco resultante. La función de cumplimiento depende del vector de desplazamiento U obtenido en el último paso y de la matriz de rigidez de la estructura K (no tengo suficiente conocimiento de la optimización de la topología para comprender de dónde proviene K; supondré que parece ser considerado directamente desde el marco).
/ *
véanse también los comentarios
(1) de
kxx y
(2) de
350 Stealth , aunque vale la pena ir a la iluminación básica [3].
* /
Y luego está hecho. Dado que todo se crea en un entorno con diferenciación automática, en esta etapa obtenemos automáticamente todos los gradientes de la función objetivo, que se empujan debido a la diferenciabilidad de todas las transformaciones en cada paso de regreso a los pesos y al vector de entrada de la red neuronal generadora. Los pesos y el vector de entrada, respectivamente, con sus derivadas parciales, cambian, causando el cambio necesario, minimizando la función objetivo. A continuación, se produce un nuevo ciclo de paso directo a través del NS -> aplicación de restricciones -> cálculo del modelo físico -> cálculo de la función objetivo -> nuevos gradientes y actualización de los pesos. Y así hasta la convergencia de Algo.
Un punto importante, cuyas descripciones no encontré en el trabajo, es cómo se selecciona el volumen total de la construcción V0, con la ayuda de la cual la solución candidata se convierte al marco en el paso 2. Obviamente, las propiedades de la solución resultante dependen extremadamente de su elección. Por indicaciones indirectas (todos los ejemplos de las soluciones obtenidas [4] tienen varias instancias que difieren precisamente en la limitación de volumen), supongo que simplemente fijan V0 en una cuadrícula determinada del rango [0.05, 0.5] y luego miran las soluciones obtenidas con diferentes ojos V0. Bueno, para un trabajo conceptual, esto, en general, es suficiente, aunque, por supuesto, sería terriblemente interesante ver también una opción con la selección de este V0, pero probablemente pasará a la siguiente etapa de desarrollo del trabajo.
El segundo punto importante, que no entendí, es cómo imponen restricciones / requisitos sobre el tipo específico de solución. Es decir si aún puede separar el puente del edificio gracias al modelo físico (el edificio tiene soporte completo y el puente está solo en los límites), entonces, ¿cómo separar, por ejemplo, un edificio de 3 pisos de un edificio de 4 pisos?
Como funciona
Resultó que para problemas pequeños (en términos del tamaño del espacio de solución = número de píxeles), el método proporciona ± la misma calidad de resultados que los mejores métodos tradicionales de optimización topológica, pero en los grandes (tamaño de cuadrícula de 2 ^ 15 o más píxeles, es decir , por ejemplo, a partir de 128 * 256 y más) obtener soluciones de alta calidad por el método es más probable que el mejor tradicional (de 116 problemas probados, el método dio una solución preferida en 99 problemas, contra 66 preferidos en el mejor tradicional).
Además, aquí comienza algo especialmente interesante. Los métodos tradicionales de optimización topológica en grandes problemas sufren el hecho de que en las primeras etapas del trabajo forman rápidamente una red a pequeña escala, que luego interfiere con el desarrollo de estructuras a gran escala. Esto lleva al hecho de que el resultado obtenido es difícil / imposible de implementar físicamente. Por lo tanto, a la fuerza hay una dirección completa en los problemas de optimización de topología que estudia / presenta métodos para hacer que las soluciones resultantes sean tecnológicamente más convenientes.
Aquí, aparentemente, gracias a la red de convolución, la optimización ocurre simultáneamente en varias escalas espaciales al mismo tiempo, lo que permite evitar / reducir en gran medida la "red" y obtener soluciones más simples, pero de alta calidad y tecnológicamente amigables.
Además, nuevamente gracias a la convolución de la red, se obtienen soluciones fundamentalmente diferentes que en los métodos tradicionales tradicionales.
Por ejemplo, en diseños:
- El método de viga en voladizo encontró una solución de solo 8 componentes, mientras que el mejor tradicional - 18.
- el método de puente de soporte delgado eligió un soporte con un patrón de ramificación en forma de árbol, mientras que el tradicional: dos soportes
- El método de techo usa columnas, mientras que el método tradicional usa un patrón de ramificación. Etc.
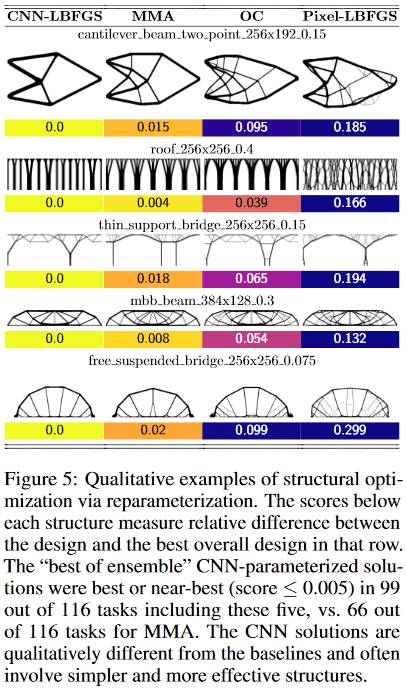
(Imagen de la publicación en cuestión)
¿Qué tiene de especial este trabajo?
Nunca he visto tal uso de una red neuronal. Por lo general, las redes neuronales se utilizan para obtener una función compleja y muy complicada y = F (x, theta) (donde x es un argumento y theta son parámetros personalizados), que pueden hacer algo útil. Por ejemplo, si x es una imagen de la cámara de un automóvil, entonces el valor y de la función puede ser, por ejemplo, una señal de si hay un peatón peligrosamente cerca del automóvil. Es decir Es importante aquí que el tipo particular de función en sí, que se usa repetidamente para resolver un problema, sea valioso.
Aquí, la red neuronal se utiliza como un astuto repositorio-modificador-ajustador de parámetros de algún modelo físico, que, debido a su propia arquitectura, impone ciertas restricciones sobre los valores y variaciones de los cambios en estos parámetros (de hecho, los ejemplos bajo el encabezado Pixel-LBFGS son un intento de optimizar píxeles directamente, no usando una red neuronal para generarlos, los resultados son visibles, el NS es importante). Aquí es donde la convolución de la red neuronal utilizada se vuelve críticamente importante, porque es su arquitectura la que le permite "captar" el concepto de invariancia de transferencia y un poco de rotación (imagine que reconoce el texto de una imagen; es importante que extraiga el texto y no importa qué partes de la imagen, se encuentra y cómo se rota, es decir, necesita la invariancia de la transferencia y la rotación). En este problema, algún tipo de bastón físico, que es una unidad de estructura y muchos de los cuales optimizamos, sigue siéndolo independientemente de su posición y orientación en el espacio.
Una red clásica totalmente conectada, por ejemplo, probablemente no funcionaría aquí (igual de bueno), porque su arquitectura permite demasiado / pequeño (bueno, sí, tal dualismo, cómo mirar). Al mismo tiempo, a pesar de que el NS sigue siendo la función muy complicada y compleja y = F (x, theta), en esta tarea no nos importa en absoluto su argumento x o sus parámetros theta y cómo se usará la función. ¡Solo nos preocupa su valor único y, que se obtiene en el proceso de optimización de una función objetivo específica para un modelo físico específico, en el que {x, theta} son solo parámetros configurables!
¡Esto, en mi opinión, es una idea increíblemente nueva y genial! (aunque, por supuesto, entonces, como siempre, puede resultar que Schmidhuber lo describió a principios de los 90, pero esperaremos y veremos)
En general, el significado del método recuerda un poco al aprendizaje reforzado: allí el NS se utiliza, en términos generales, como un "depósito de experiencia" de un agente que actúa en un determinado entorno, que se actualiza a medida que el entorno recibe comentarios sobre las acciones del agente. Solo allí, este mismo "depósito de experiencia" se usa constantemente para tomar nuevas decisiones por parte del agente, y aquí es solo un depósito de parámetros del modelo físico, del cual solo estamos interesados en el único resultado final de la optimización.
Bueno, el ultimo. Un momento interesante me llamó la atención.
Así es como se ven las soluciones óptimas para la tarea de un edificio de varios pisos:
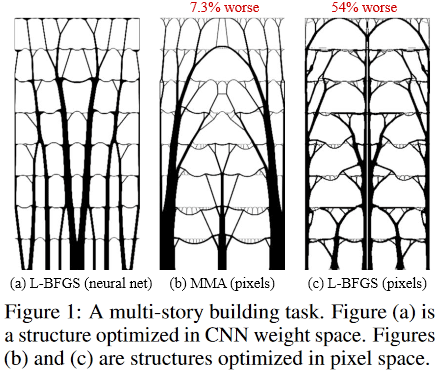
(Imagen de la publicación en cuestión)
Y entonces:

ubicado dentro de la fantástica Sagrada Familia, el Templo de la Sagrada Familia, ubicado en Barcelona, España, que fue "diseñado" por el brillante Antonio Gaudí.
Agradecimientos
Agradezco al primer autor del artículo, Stephan Hoyer, por su pronta asistencia para explicar algunos detalles oscuros del trabajo, así como a los participantes de Habr que hicieron sus adiciones y / o ideas provocativas útiles.
[1]
opción para determinar el problema de optimización estructural / topológica[2]
"Desarrollos en topología y optimización de formas"[3] Andreassen, E., Clausen, A., Schevenels, M., Lazarov, BS y Sigmund, O. Optimización eficiente de la topología en MATLAB utilizando 88 líneas de código. Optimización estructural y multidisciplinaria, 43 (1): 1–16, 2011. Una versión preliminar de este trabajo y el código están disponibles en
http://www.topopt.mek.dtu.dk/Apps-and-software/Efficient-topology-optimization-in -MATLAB[4]
ejemplos de soluciones de trabajo[5] Códigos fuente de trabajo:
https://github.com/google-research/neural-structural-optimization
Ver también
Última actualización de esta publicación 2020.01.23 09:18