En esta publicación, hablaremos sobre el lenguaje JetBrains recientemente lanzado con tipos dependientes de Arend (el idioma lleva el nombre de
Gating Rent ). Este lenguaje ha sido desarrollado por
JetBrains Research en los últimos años. Aunque los repositorios hace un año se pusieron a disposición del público en
github.com/JetBrains , el lanzamiento completo de Arend solo ocurrió en julio de este año.
Intentaremos decir cómo Arend difiere de los sistemas existentes de matemática formalizada basados en tipos dependientes, y qué funcionalidad está ahora disponible para sus usuarios. Suponemos que el lector de este artículo generalmente está familiarizado con los tipos dependientes y ha escuchado al menos uno de los idiomas en función de los tipos dependientes: Agda, Idris, Coq o Lean. Sin embargo, no esperamos que el lector tenga tipos dependientes en un nivel avanzado.
Por simplicidad y concreción, nuestra historia sobre Arend y los tipos de homotopía irá acompañada de la implementación en Arend del algoritmo de clasificación de listas más simple; incluso con este ejemplo, puede sentir la diferencia entre Arend y Agda y Coq. Ya hay una serie de artículos sobre Habré dedicados a los tipos dependientes. Digamos sobre la implementación de listas de clasificación utilizando el método QuickSort en Agda, existe
un artículo de este tipo . Implementaremos un algoritmo más simple para ordenar inserciones. En este caso, nos centraremos en las construcciones del lenguaje Arend, y no en el algoritmo de clasificación en sí.
Entonces, la principal diferencia entre Arend y otros lenguajes con tipos dependientes es la teoría lógica en la que se basa. Arend utiliza como tal la teoría del tipo de homotopía
V. Voevodsky recientemente descubierta (
HoTT ). Más específicamente, Arend se basa en una variación de HoTT llamada "teoría de tipos con espaciado". Recuerde que Coq se basa en el llamado cálculo de construcciones inductivas (Cálculo de construcciones inductivas), mientras que Agda e Idris se basan en la
teoría intensiva de tipos de Martin-Löf . El hecho de que Arend se base en HoTT afecta significativamente sus construcciones sintácticas y la operación del algoritmo de verificación de tipos (Typcheker). Vamos a discutir estas características en este artículo.
Tratemos de describir brevemente el estado de la infraestructura del lenguaje. Para Arend hay un complemento para IntelliJ IDEA, que se puede instalar directamente desde el repositorio de complementos IDEA. En principio, instalar el complemento es suficiente para trabajar completamente con Arend, aún no necesita descargar e instalar nada. Además de la verificación de tipos, el complemento Arend proporciona una funcionalidad familiar para los usuarios de IDEA: hay resaltado y alineación del código, varias refactorizaciones y consejos. También existe la opción de usar la versión de consola de Arend. Puede encontrar una descripción más detallada del proceso de instalación
aquí .
Los ejemplos de código en este artículo se basan en la biblioteca estándar de Arend, por lo que recomendamos descargar su código fuente del
repositorio . Después de la descarga, el directorio de origen debe importarse como un proyecto IDEA utilizando el comando Importar proyecto. En Arend, algunas secciones de la teoría del tipo de homotopía y la teoría del anillo ya se han formalizado. Por ejemplo, en la biblioteca estándar hay una implementación del anillo de números racionales Q junto con pruebas de todas las propiedades teóricas del anillo requeridas.
La
documentación detallada del
lenguaje , en la que muchos de los puntos cubiertos en este artículo se explican con más detalle, también es de dominio público. Puede hacer preguntas directamente a los desarrolladores de Arend en el
canal de telegramas .
1. Descripción general de HoTT / Arend
La teoría de tipo de homotopía (o, en resumen, HoTT) es un tipo de teoría de tipo intensional que difiere de la teoría de tipo clásica de Martin-Löf (MLTT, en la que se basa Agda) y el cálculo de construcción inductivo (CIC, en el que se basa Coq), en eso, junto con declaraciones y conjuntos contienen los llamados tipos de un nivel de homotopía más alto.
En este artículo, no nos fijamos el objetivo de explicar los fundamentos de HoTT en detalle: para una exposición detallada de esta teoría, sería necesario volver a contar todo el libro (ver
esta publicación ). Solo notamos que una teoría basada en la axiomática de HoTT es, en cierto sentido, mucho más elegante e interesante que la teoría clásica del tipo Martin-Löf. Por lo tanto, una serie de axiomas que anteriormente debían postularse adicionalmente (por ejemplo, extensionalidad funcional) se prueban en HoTT como teoremas. Además, en HoTT, uno puede definir internamente esferas de homotopía multidimensionales e incluso contar algunos de sus
grupos de homotopía .
Sin embargo, estos aspectos de HoTT son principalmente interesantes para los matemáticos, y el propósito de este artículo es explicar cómo el Arend basado en HoTT se compara favorablemente con Agda / MLTT y Coq / CIC con el ejemplo de representar a las entidades programadoras tan simples y familiares como las listas ordenadas. Al leer este artículo, es suficiente tratar a HoTT como una especie de teoría de tipo intensional con una axiomática más desarrollada, lo que brinda comodidad al trabajar con universos e igualdades.
1.1 Tipos dependientes, correspondencia de Curry - Howard, universos
Recuerde que los lenguajes con tipos dependientes difieren de los lenguajes de programación funcional ordinarios en que, además de los tipos de datos habituales, como listas o números naturales, hay tipos que dependen del valor del parámetro. Los ejemplos más simples de tales tipos son vectores de una longitud dada n o árboles equilibrados de una profundidad dada d.
Aquí se mencionan algunos ejemplos adicionales de tales tipos
.Recuerde que la
correspondencia de Curry - Howard le permite a uno interpretar declaraciones de lógica como tipos dependientes. La idea principal de esta correspondencia es que un tipo vacío corresponde a una declaración falsa, y los tipos poblados corresponden a una declaración verdadera. Los elementos tipo pueden considerarse como pruebas de la declaración lógica correspondiente. Por ejemplo, cualquier elemento como los enteros puede considerarse como una prueba del hecho de que existen enteros (es decir, el tipo de enteros está poblado).
Las diferentes construcciones naturales sobre tipos corresponden a diferentes conectivos lógicos:
- El producto de los tipos A × B a veces se llama el tipo del par Par A B. Dado que este tipo se llena si y solo si se llenan ambos tipos A y B, esta construcción corresponde a la lógica “y”.
- La suma de los tipos A + B. En Haskell, este tipo se llama A B. Ya que este tipo se llena si y solo si se llena uno de los tipos A o B, esta construcción corresponde a un "o" lógico.
- Tipo funcional A → B. Cualquier función de este tipo convierte elementos de A en elementos de B. Por lo tanto, dicha función existe exactamente cuando la existencia de un elemento de tipo A implica la existencia de un elemento de tipo B. Por lo tanto, esta construcción corresponde a implicación.
Supongamos ahora que se nos da un cierto tipo A y una familia de tipos B parametrizados por un elemento a de tipo A. Veamos ejemplos de construcciones más complejas sobre tipos dependientes.
- Tipo de función dependiente Π (a: A) (B a). Este tipo coincide con el tipo funcional habitual A → B si B es independiente de A. Una función de tipo Π (a: A) (B a) convierte cualquier elemento a de tipo A en un elemento de tipo B a. Por lo tanto, dicha función existe si y solo si, para cualquier a : A, existe un elemento B a. Por lo tanto, esta construcción corresponde al cuantificador universal ∀. Para el tipo funcional dependiente, Arend usa la sintaxis
\Pi (x : A) -> B a , y el término que habita este tipo puede construirse usando la expresión lambda \lam (a : A) => f a. - El tipo de pares dependientes es Σ (a: A) (B a). Este tipo coincide con los tipos habituales de pares A × B si B es independiente de A. El tipo Σ (a: A) (B a) se rellena exactamente cuando existe un elemento a: A y un elemento de tipo B a. Por lo tanto, este tipo corresponde al cuantificador de existencia
∃ . El tipo de pares dependientes en Arend se denota por \Sigma (a : A) (B a) , y los términos que lo habitan se construyen utilizando el constructor del par (a, b) dependiente) (a, b) .
- El tipo de igualdad es a = a ', donde a y a' son dos elementos de algún tipo A. Dicho tipo se rellena si a y a 'son iguales y, de lo contrario, está vacío. Obviamente, este tipo es un análogo del predicado de igualdad en la lógica.
En este punto, remitimos al lector a fuentes en las que se discute la correspondencia de Curry - Howard con más detalle (véase, por ejemplo, un
curso de conferencias o artículos
aquí o
aquí ).
Todas las expresiones consideradas en la teoría de tipos deben tener algún tipo. Dado que las expresiones que denotan tipos también se consideran en el marco de esta teoría, también se les debe asignar un cierto tipo. La pregunta es, ¿qué tipo de tipo debería ser?
La primera decisión ingenua que viene a la mente es asignar a todos los tipos un tipo formal
\Type , llamado
universo (se llama así porque contiene todos los tipos en general). Si usamos este universo, las construcciones de suma y los productos de tipo mencionados anteriormente recibirán la firma
\Type → \Type → \Type , y las construcciones más complejas del producto dependiente y la suma dependiente recibirán la firma
Π (A : \Type) → ((A → \Type) → \Type) .
En este punto, surge la pregunta, ¿qué tipo debería tener el universo
\Type ? Un intento ingenuo de decir que el tipo de universo
\Type , por definición, es
\Type sí mismo conduce a
la paradoja de Girard , por lo que, en lugar de un solo universo
\Type considere una
jerarquía infinita
de universos , es decir. la cadena anidada de universos
\Type 1 < \Type 2 < … , cuyos niveles están numerados por números naturales, y el tipo de universo
\Type i , por definición, es el universo
\Type (i+1) . Para las construcciones de tipo mencionadas anteriormente, también se deben introducir
firmas más
complejas .
Por lo tanto, se necesitan universos en la teoría de tipos para que cualquier expresión tenga un cierto tipo. En algunas variedades de teoría de tipos, los universos se usan para otro propósito: distinguir entre variedades de tipos. Ya hemos visto que los conjuntos y las declaraciones son casos especiales de tipos. Esto muestra que podría tener sentido introducir en la teoría un universo Prop separado para declaraciones y una jerarquía separada de universos Set
i para conjuntos. Este es exactamente el enfoque utilizado en Cálculo de construcciones inductivas, la teoría en la que se basa el sistema Coq.
1.2 Ejemplos de tipos inductivos más simples y funciones recursivas
Considere las definiciones en Arend de los tipos de datos inductivos más simples: tipo booleano, tipo de número natural y listas polimórficas. Arend usa la palabra clave
\data para introducir nuevos tipos inductivos.
\data Empty -- ,
\data Bool
| true
| false
\data Nat
| zero
| suc Nat
\data List (A : \Set)
| nil
| \infixr 5 :-: A (List A)Como puede ver en los ejemplos anteriores, después de la palabra clave
\data , debe especificar el nombre del tipo inductivo y una lista de sus constructores. Al mismo tiempo, el tipo de datos y los constructores pueden tener algunos parámetros. Digamos que en el ejemplo anterior, el tipo de
List tiene un parámetro
A El constructor de la lista
nil no tiene parámetros, y el constructor: -: tiene dos parámetros (uno de los cuales es del tipo
A y el otro es del tipo
List A ). El universo
\Set consta de tipos que son conjuntos (la definición de conjuntos se dará en la siguiente sección). La
\infixr permite utilizar la notación infija para el constructor: -: y, además, le dice al analizador Arend que el operador: -: es una operación de asociación correcta con prioridad 5.
En Arend, todas las palabras clave comienzan con un carácter de barra diagonal inversa ("\"), una implementación inspirada en LaTeX. Solo tenga en cuenta que las reglas léxicas en Arend son muy liberales:
Circle_HSpace, contrFibers=>Equiv, suc/=0, zro_*-left e even
n:Nat - todos estos literales son ejemplos de identificadores válidos en Arend. El último ejemplo muestra lo importante que es para el usuario de Arend
recordar poner espacios entre los identificadores y los dos puntos . Tenga en cuenta que en los identificadores Arend no está permitido usar caracteres Unicode (en particular, no puede usar cirílico).
Arend usa la palabra clave
\func para definir funciones. La sintaxis de esta construcción es la siguiente: después de la palabra clave
\func , debe especificar el nombre de la función, sus parámetros y el tipo del valor de retorno. El elemento final para definir una función es su cuerpo.
Si es posible especificar explícitamente la expresión en la que se calculará la función dada, entonces token => se usa para indicar el cuerpo de la función. Considere, por ejemplo, la definición de una función de negación de tipo.
\func Not (A : \Type) : \Type => A -> Empty
El tipo de retorno de una función no siempre tiene que especificarse explícitamente. En el ejemplo anterior, Arend podría inferir independientemente el tipo
Not , y podríamos omitir la expresión ":
\Type " después de los corchetes.
Como en la mayoría de los sistemas matemáticos formalizados, el usuario no tiene que especificar un nivel predictivo explícito para el universo
\Type , y las definiciones en las que se usan universos sin especificar explícitamente un nivel predictivo se consideran
polimórficas .
Ahora intentemos definir una función que calcule la longitud de la lista. Dicha función es fácil de identificar mediante la coincidencia de patrones. Arend usa la palabra clave
\elim para esto. Después de eso, debe especificar las variables por las cuales se realiza la comparación (si hay más de una variable, entonces deben escribirse con una coma). Si la comparación se realiza para todos los parámetros explícitos, entonces se puede omitir
\elim junto con las variables. Esto es seguido por un bloque de puntos de comparación, separados entre sí por una barra vertical "|". Cada elemento en este bloque es una expresión de la forma
«, » => «» .
\func length {A : \Set} (l : List A) : Nat | nil => 0 | :-: x xs => suc (length xs)
En el ejemplo anterior, el parámetro A de la función de
length está rodeado de llaves. Estos corchetes en Arend se usan para denotar argumentos implícitos, es decir argumentos que el usuario puede omitir al llamar a una función o al usar un tipo. Tenga en cuenta que en Arend no puede usar la notación de infijo para designar constructores cuando coincida con un patrón, por lo que la notación de prefijo se usa en el ejemplo de muestra.
Al igual que en Coq / Agda, en Arend se debe garantizar que todas las funciones se completen (es decir, la verificación de terminación está presente en Arend). En la definición de la función de longitud, esta verificación es exitosa, ya que una llamada recursiva reduce estrictamente el primer argumento explícito. Si tal reducción no ocurriera, Arend emitiría un mensaje de error.
\func bad : Nat => bad [ERROR] Termination check failed for function 'bad' In: bad
Arend permite dependencias circulares y funciones recursivas para las cuales también se realizan verificaciones de finalización. El algoritmo de esta verificación se implementa en base al
artículo de A. Abel. En él encontrará una descripción más detallada de las condiciones que deben cumplir las funciones recursivas mutuas.
1.3 ¿Cómo difieren los conjuntos de las declaraciones?
Anteriormente escribimos que ejemplos de tipos son conjuntos y declaraciones. Además, utilizamos las palabras clave
\Type y
\Set para denotar universos en Arend. En esta sección, trataremos de explicar con más detalle cómo las declaraciones difieren de los conjuntos en términos de variedades de la teoría de tipo intensional (MLTT, CIC, HoTT), y al mismo tiempo explicaremos en qué consiste el significado de las palabras clave
\Prop ,
\Set y
\Type en Arend.
Recuerde que en la teoría clásica de Martin-Löf no hay separación de tipos en conjuntos y enunciados. En particular, en teoría solo hay un universo acumulativo (que se denota ya sea por Establecer en Agda, o Escribir en Idris, o Ordenar en Lean). Este enfoque es el más simple, pero hay situaciones en las que se manifiestan sus deficiencias. Supongamos que estamos tratando de implementar el tipo de "lista ordenada" como un par dependiente que consiste en una lista y prueba de su orden. Resulta que, en el marco del MLTT "puro", no será posible demostrar la igualdad de las listas ordenadas que consisten en elementos idénticos, que al mismo tiempo difieren en términos de prueba de pedido. Tener tal igualdad sería muy natural y deseable, por lo que la imposibilidad de demostrarlo puede considerarse como un defecto teórico en MLTT.
En Agda, este problema se resuelve parcialmente con la ayuda de las llamadas anotaciones de inmaterialidad (consulte la
fuente , en la que se analiza el ejemplo de la lista con más detalle). Sin embargo, estas anotaciones no son una construcción de la teoría MLTT, ni son construcciones completas en los tipos (es imposible marcar con una anotación de tipo que no se utiliza en el argumento de la función).
En CIC, basado en CIC, hay dos universos diferentes anidados entre sí:
Prop (el universo de sentencias) y
Set (el universo de conjuntos), que están inmersos en la jerarquía integral de universos
Type . La principal diferencia entre
Prop y
Set es que hay una serie de restricciones en las variables cuyo tipo pertenece a
Prop en Coq. Por ejemplo, no se pueden usar en los cálculos, y la comparación con la muestra para ellos solo es posible dentro de la evidencia de otras declaraciones. Por otro lado, todos los elementos del tipo que pertenece al universo
Prop son iguales en el axioma de evidencia intrascendente, vea la declaración en
Coq.Logic.ProofIrrelevance . Usando este axioma, podríamos probar fácilmente la igualdad de las listas ordenadas mencionadas anteriormente.
Finalmente, considere el enfoque Arend / HoTT para las declaraciones y universos. La principal diferencia es que HoTT prescinde del axioma de la evidencia intrascendente. Es decir, no hay un axioma especial en HoTT que postule que todos los elementos de las declaraciones son iguales. Pero en HoTT, un tipo,
por definición , es una declaración si se puede demostrar que todos sus elementos son iguales entre sí. Podemos definir un predicado sobre tipos que sea verdadero si el tipo es una declaración:
\func isProp (A : \Type) => \Pi (aa' : A) -> a = a'
Surge la pregunta: ¿qué tipos satisfacen este predicado, es decir, son declaraciones? Es fácil verificar que esto sea cierto para los tipos vacío y singleton. Para los tipos donde hay al menos dos elementos diferentes, esto ya no será cierto.
Por supuesto, queremos que todas las conexiones lógicas necesarias se definan sobre las declaraciones. En la Sección 1.1, ya discutimos cómo podrían determinarse utilizando construcciones teóricas de tipo. Sin embargo, existe el siguiente problema: no todas las operaciones que hemos ingresado conservan la propiedad
isProp . Las construcciones del producto de tipos y el tipo funcional (dependiente) conservan esta propiedad, mientras que las construcciones de la suma de tipos y pares dependientes no. Por lo tanto, no podemos usar la disyunción y el cuantificador de la existencia.
Este problema se puede resolver con la ayuda de una nueva construcción, que se agrega a HoTT, el llamado
truncamiento proposicional . Este diseño le permite convertir cualquier tipo en una declaración. Se puede considerar como una operación formal, igualando todos los términos que habitan este tipo. Esta operación es algo similar a las anotaciones de inmaterialidad de Agda, sin embargo, a diferencia de ellas, es una operación completa en los tipos con firma
\Type -> \Prop .
El último ejemplo importante de declaraciones es la igualdad de dos elementos de algún tipo. Resulta que, en el caso general, el tipo de igualdad
a = a' no tiene que ser una declaración. Los tipos para los cuales es uno se llaman conjuntos:
\func isSet (A : \Type) => \Pi (aa' : A) -> isProp (a = a')
Todos los tipos que se encuentran en los lenguajes de programación ordinarios satisfacen este predicado, es decir, la igualdad en ellos es una declaración. Por ejemplo, esto es cierto para números naturales, enteros, productos de conjuntos, sumas de conjuntos, funciones sobre conjuntos, listas de conjuntos y otros tipos de datos inductivos construidos a partir de conjuntos. Esto significa que si solo estamos interesados en construcciones tan familiares, entonces no podemos pensar en tipos arbitrarios que no satisfagan este predicado. Todos los tipos encontrados en Coq son
conjuntos .
Los tipos que no son conjuntos se vuelven útiles si desea abordar la teoría de tipos de homotopía. Por ahora, simplemente remitimos al lector al
módulo de biblioteca estándar que contiene la definición de una
esfera n-dimensional , un ejemplo de un tipo que no es un conjunto.
Arend tiene universos especiales
\Prop y
\Set , que consisten en declaraciones y conjuntos, respectivamente. Si ya sabemos que el tipo A está contenido en el universo
\Prop (o
\Set ), entonces la prueba de la
isProp (o
isSet ) correspondiente en Arend puede obtenerse usando el axioma
Path.inProp integrado en el
preludio (damos un ejemplo del uso de este axioma en la sección 2.3).
\func inProp {A : \Prop} : \Pi (aa' : A) -> a = a'
Ya hemos notado que no todas las construcciones naturales en tipos retienen la propiedad
isProp . Por ejemplo, los tipos de datos inductivos con dos o más constructores nunca lo satisfacen. Como se señaló anteriormente, podemos usar la construcción de
truncamiento proposicional que convierte cualquier tipo en una declaración.
En la biblioteca Arend, la implementación estándar del truncamiento proposicional se llama
Logic.TruncP . Podríamos definir un tipo de "o" lógico en Arend como truncar la suma de tipos:
\data \fixr 2 Or (AB : \Type) -- Sum of types; analogue of Coq's type "sum" | inl A | inr B \func \infixr 2 || (AB : \Type) => TruncP (sum AB) -- Logical “or”, analogue of Coq's type "\/"
En Arend, hay otra forma más simple y conveniente de definir un tipo inductivo truncado proposicionalmente. Para hacer esto, simplemente agregue la palabra clave
\truncated antes de definir el tipo de datos. Por ejemplo, la definición de un "o" lógico en la biblioteca estándar de Arend se da de la siguiente manera.
\truncated \data \infixr 2 || (AB : \Type) : \Prop -- Logical “or”, analogue of Coq's type "\/" | byLeft A | byRight B
El trabajo adicional con tipos truncados proposicionalmente se asemeja al de los tipos asignados al universo
Prop en Coq. Por ejemplo, la coincidencia de patrones de una variable cuyo tipo es una declaración solo se permite en una situación en la que el tipo de expresión que se define es en sí misma una declaración. Por lo tanto, siempre es fácil definir la función
Or-to-|| a través de la comparación con la muestra, pero la función inversa a ella, solo si el tipo A
`Or` B es una declaración (lo cual es bastante raro, por ejemplo, cuando los tipos
A y
B son declaraciones y se excluyen mutuamente).
\func Or-to-|| {AB : \Prop} (a-or-b : A `Or` B) : A || B | inl a => byLeft a | inr b => byRight
Recuerde también que la peculiaridad del mecanismo de universos en Coq es que si se asignó alguna definición al universo
Prop , entonces de ninguna manera será posible usarlo en el cálculo. Por esta razón, los desarrolladores de Coq
no recomiendan el uso de construcciones proposicionales, pero aconsejan reemplazarlas con análogos del universo de conjuntos, si es posible. El mecanismo de los universos Arend no tiene este inconveniente, es decir, en ciertas situaciones es posible usar declaraciones en los cálculos. Daremos un ejemplo de tal situación cuando discutamos la implementación del algoritmo de clasificación de listas.
1.4 Clases en Arend
Dado que nuestro objetivo es implementar el algoritmo de clasificación más simple, parece útil familiarizarse con la implementación de conjuntos ordenados disponibles en la biblioteca estándar de Arend.
En Arend, las clases se usan para encapsular operaciones y axiomas que definen estructuras matemáticas, y también para resaltar las relaciones entre estas estructuras usando la herencia. Las clases también son espacios de nombres, dentro de los cuales es conveniente colocar construcciones y teorías con un significado apropiado.
La clase base de la que se heredan todas las clases de orden en Arend es la clase
BaseSet , que no contiene ningún miembro que no sea la designación
E para el conjunto de hosts (es decir, el conjunto en el que las
BaseSet descendientes de
BaseSet ya introducen varias operaciones). Considere la definición de esta clase de la biblioteca estándar de Arend.
\class BaseSet (E : \Set) -- ,
En la definición anterior, el operador
E declara un parámetro de clase. Uno puede preguntarse, ¿hay alguna diferencia en la definición anterior de
BaseSet de la siguiente definición, en la cual el operador E se define como un campo de clase?
\class BaseSet' -- | E : \Set
Una respuesta ligeramente inesperada es que en Arend
no hay diferencia entre las dos definiciones en el sentido de que cualquier parámetro de clase (incluso implícito) en Arend, de hecho,
es su campo. Por lo tanto, para ambas implementaciones de
BaseSet , uno podría usar la expresión
xE para acceder al campo E.
BaseSet una diferencia entre las variantes anteriores de la definición de
BaseSet , pero es más sutil, la examinaremos con más detalle en la siguiente sección cuando analicemos las instancias de clase ( instancias de clase).
La operación de ordenar una lista tiene sentido solo si se especifica un orden lineal en el tipo de objetos en la lista, por lo tanto, primero consideramos las definiciones de un conjunto
estrictamente ordenado parcialmente y un
conjunto ordenado linealmente. \class StrictPoset \extends BaseSet { | \infix 4 < : E -> E -> \Prop | <-irreflexive (x : E) : Not (x < x) | <-transitive (xyz : E) : x < y -> y < z -> x < z } \class LinearOrder \extends StrictPoset { | <-comparison (xyz : E) : x < z -> x < y || y < z | <-connectedness (xy : E) : Not (x < y) -> Not (y < x) -> x = y }
Desde el punto de vista de la teoría de tipos, las clases en Arend pueden considerarse como análogos de tipos sigma con una sintaxis más conveniente para proyecciones y constructores. , Arend- -, .
,
. , . , StrictPoset
<-irreflexive <-transitive ,
E < — . , (, , ) , .
, , . , Arend
, , . , . , , , , .
:
\class DecSet \extends BaseSet | decideEq (xy : E) : Dec (x = y)
Dec ,
Dec E ,
E ,
E ,
E .
\data Dec (E : \Prop) | yes E | no (Not E)
, ,
Dec ( decidable)
Order.LinearOrder . Dec , , ,
trichotomy , ,
E , <. ,
Dec Comparable Java.
\class Dec \extends LinearOrder, DecSet { | trichotomy (xy : E) : (x = y) || (x < y) || (y < x) | <-comparison xyz x<z => {?} -- | <-connectedness xyx/<yy/<x => {?} | decideEq xy => {?} }
Dec Dec , , , , .
Dec , .
,
Dec ( ).
Dec , Arend (
Dec LinearOrder, DecSet ), , (diamond inheritance).
: , ( , ).
Dec Order.LinearOrder IDEA ( [Ctrl]+[H]), , .
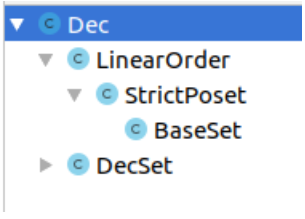
Arend ( IDEA
BaseSet ). , .
1.5 , , .
StrictPoset Nat. Arend , . -, , , - ( ), .
: . .
data \infix 4 < (ab : Nat) \with | zero, suc _ => zero<suc_ | suc a, suc b => suc<suc (a < b) \lemma irreflexivity (x : Nat) (p : x < x) : Empty | suc a, suc<suc a<a => irreflexivity a a<a \lemma transitivity (xyz : Nat) (p : x < y) (q : y < z) : x < z | zero, suc y', suc z', zero<suc_, suc<suc y'<z' => zero<suc_ | suc x', suc y', suc z', suc<suc x'<y', suc<suc y'<z' => suc<suc (transitivity x' y' z' x'<y' y'<z')
\func \lemma . , , , . ,
\lemma ,
\Prop .
x'<y' — -,
x' < y' . - (.. , , ).
(instance)
StrictPoset. Arend tiene varias opciones de sintaxis diferentes para esto. La primera forma de crear una instancia de una clase es usar una palabra clave \newdentro de cualquier expresión. En este caso, se creará una "instancia de clase anónima". \func NatOrder => \new StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity }
StrictPoset { … } \new : -
StrictPoset . - , , ,
\new .
\new C { … } C { … } . C, C. , ,
NatOrder StrictPoset .
, . ,
StrictPoset Nat StrictPoset { | E => Nat } . ,
NatOrder StrictPoset , ( ).
NatOrder \cowith ( - ).
\func NatOrder : StrictPoset \cowith { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity }
, ,
\instance. \instance NatOrder : StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity }
Arend , Haskell.
NatOrder \instance \cowith ,
StrictPoset ( ).
,
BaseSet - E ( ), , E . .
, Arend . Arend , , ( , «
»
\classifying \field , Arend ). :
- Arend . ,
X StrictPoset , List X List XE .
- Arend .
, . ,
\instance StrictPoset ,
Nat Int (
NatOrder IntOrder ).
,
x < y , x, y , , x, y . Arend ,
NatOrder.< , —
IntOrder.< .
, . Arend , <
StrictPoset , E. , Arend
x<y StrictPoset ( ), E . ,
< .
, Arend. ,
\use \coerce . Arend
- algún espacio de nombres utilizado para colocar varias construcciones auxiliares en él. Para agregar cualquier otra definición al módulo de definición asociado, se usa la palabra clave \where.Considere el ejemplo más simple de usar un mecanismo de conversión de tipo. La función fromNatse usará para convertir implícitamente números naturales a enteros. \data Int | pos Nat | neg Nat \with { zero => pos zero } \where { \use \coerce fromNat (n : Nat) => pos n }
\use \coerce \func , . , , (, , ).
:
HoTT JetBrains Research.