Me encontré con un rompecabezas interesante: de hecho, se dan el número a y el número entero positivo n. Calcule la enésima raíz de un número sin usar bibliotecas.
Datos de entrada: el número a es real, no negativo, no excede 1000, se especifica con una precisión de 6 decimales. El número n es natural, no supera los 10.
Salida: El programa debe generar un solo número: la respuesta al problema con una precisión de al menos 5 decimales.
Naturalmente, fue interesante resolverlo en un borrador con un lápiz, y luego dibujarlo en el editor e intentar compilarlo. Sin buscar en Google, consejos y aún más utilizando bibliotecas. Si decide esto por primera vez, primero intente escribir un programa para encontrar la raíz cuadrada habitual. Si le resulta difícil la tarea, resuelva casi lo mismo, pero más simple. Entonces su miedo desaparecerá y surgirá algún tipo de comprensión aproximada.
Entonces, para empezar, daré un ejemplo de cómo calcular la raíz cuadrada sin usar una función de biblioteca. Algoritmo de iteración secuencial. Converge bastante rápido incluso para grandes números.
#include <stdio.h> int main(void) { double num = 570.15; double root = num / 2; double eps = 0.01; int iter = 0; while( root - num / root > eps ){ iter++; root = 0.5 * (root + num / root); printf("Iteration: %d : root = %f\n", iter, root); } printf("root = %f", root); return 0; }
Puede ejecutar el código aquí:
HAGA CLIC¿La complejidad logarítmica del algoritmo? U otro? :)
Ahora puede pasar a la versión complicada de la tarea. En este caso, la solución es más generalizada.
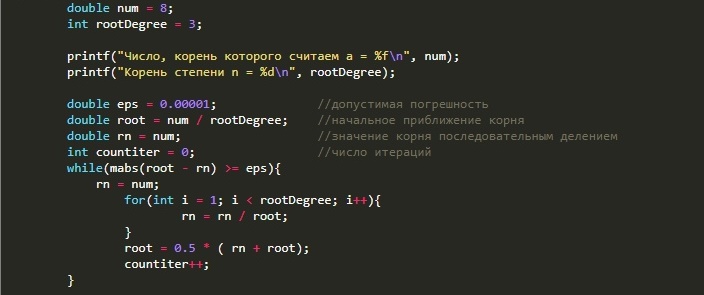
#include <stdio.h> double mabs(double x){ return (x < 0)? -x : x; } int main(void) { double num = 8; int rootDegree = 3; printf(", = %f\n", num); printf(" n = %d\n", rootDegree); double eps = 0.00001; // double root = num / rootDegree; // double rn = num; // int countiter = 0; // while(mabs(root - rn) >= eps){ rn = num; for(int i = 1; i < rootDegree; i++){ rn = rn / root; } root = 0.5 * ( rn + root); countiter++; } printf("root = %f\n", root); printf(" = %i\n", countiter); return 0; }
Puede ejecutar el código aquí:
HAGA CLICEn esta solución, uso la idea de una aproximación inicial relativamente buena. Entonces la división secuencial es la segunda aproximación de la raíz del enésimo grado. A continuación, se considera una nueva aproximación promediando las dos actuales. Consistentemente, el algoritmo converge a la raíz deseada con un error predeterminado. Esto es un poco como un método de iteración simple.
Este es el primer algoritmo de trabajo escrito en la rodilla. Todavía necesitamos reflexionar sobre la complejidad y las posibilidades de la aceleración. Por cierto, ¿qué características de aceleración de este algoritmo se pueden implementar en su opinión?
Siento que habrá una pregunta: "¿Por qué hacer esto si todo se implementó en bibliotecas hace cien años?"
Respuesta: Personalmente, siempre me gustó pensar en algoritmos que ya están implementados en bibliotecas estándar. Trate de desarrollarlos usted mismo (bueno, o desarrollar algún tipo de parodia lenta y fracasar). Entrena muy bien el cerebro. Por lo tanto, en mi opinión, "reinventar la rueda" es muy útil. Y es categóricamente dañino usar siempre todo listo, sin ninguna idea de la estructura interna.