Oh este método de Newton

Se ha escrito mucho sobre los métodos de optimización numérica. Esto es comprensible, especialmente en el contexto de los éxitos recientemente demostrados por las redes neuronales profundas. Y es muy gratificante que al menos algunos entusiastas estén interesados ​​no solo en cómo bombardear su red neuronal en los marcos que han ganado popularidad en Internet, sino también en cómo y por qué todo funciona. Sin embargo, recientemente tuve que señalar que al plantear problemas relacionados con el entrenamiento de las redes neuronales (y no solo con el entrenamiento, y no solo con las redes), incluso en Habré, cada vez con más frecuencia se utilizan varias declaraciones "conocidas" para el reenvío, cuya validez para decirlo suavemente, dudoso. Entre tales declaraciones dudosas:

1. Los métodos de la segunda y más órdenes no funcionan bien en las tareas de entrenamiento de redes neuronales. Porque eso
2. El método de Newton requiere una definición positiva de la matriz de Hesse (segundas derivadas) y, por lo tanto, no funciona bien.
   
3. El método de Levenberg-Marquardt es un compromiso entre el descenso de gradiente y el método de Newton y generalmente es heurístico.
   

etc. Que continuar con esta lista, es mejor ponerse manos a la obra. En esta publicación consideraremos la segunda declaración, ya que solo lo conocí al menos dos veces en Habré. Tocaré la primera pregunta solo en la parte relativa al método de Newton, ya que es mucho más extensa. El tercero y el resto quedarán hasta tiempos mejores.

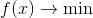
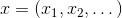
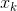
El foco de nuestra atención será la tarea de optimización incondicional. donde - un punto de espacio vectorial, o simplemente - un vector. Naturalmente, esta tarea es más fácil de resolver, cuanto más sepamos sobre . Por lo general, se supone que es diferenciable con respecto a cada argumento , y tantas veces como sea necesario para nuestros actos sucios. 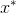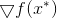Es bien sabido que una condición necesaria para eso en un punto se alcanza el mínimo, es la igualdad del gradiente de la función en este punto cero Desde aquí obtenemos instantáneamente el siguiente método de minimización:

Resuelve la ecuación .

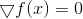
La tarea, por decirlo suavemente, no es fácil. Definitivamente no es más fácil que el original. Sin embargo, en este punto, podemos notar de inmediato la conexión entre el problema de minimización y el problema de resolver un sistema de ecuaciones no lineales. Esta conexión volverá a nosotros cuando consideremos el método Levenberg-Marquardt (cuando lleguemos a él). Mientras tanto, recuerde (o descubra) que uno de los métodos más utilizados para resolver sistemas de ecuaciones no lineales es el método de Newton. Consiste en el hecho de que para resolver la ecuación partimos de una aproximación inicial construir una secuencia

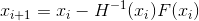
- Método explícito de Newton

o

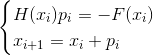
- Método implícito de Newton

donde - matriz compuesta de derivadas parciales de una función . Naturalmente, en el caso general, cuando el sistema de ecuaciones no lineales simplemente se nos da en sensaciones, requiere algo de la matriz No tenemos derecho. En el caso de que la ecuación sea una condición mínima para alguna función, podemos afirmar que la matriz simétrico Pero no mas.

El método de Newton para resolver sistemas de ecuaciones no lineales se ha estudiado bastante bien. Y aquí está la cosa: para su convergencia no se requiere la definición positiva de la matriz . Sí, y no puede ser requerido; de lo contrario, no habría servido para nada. En cambio, hay otras condiciones que aseguran la convergencia local de este método y que no consideraremos aquí, enviando a las personas interesadas a literatura especializada (o en el comentario). Obtenemos que la afirmación 2 es falsa.

Entonces?

Si y no La emboscada aquí en la palabra es la convergencia local antes de la palabra. Significa que la aproximación inicial debe estar "lo suficientemente cerca" de la solución, de lo contrario, en cada paso seremos más y más alejados de ella. Que hacer No entraré en detalles sobre cómo se resuelve este problema para sistemas de ecuaciones no lineales de forma general. En cambio, volvamos a nuestra tarea de optimización. El primer error de la declaración 2 es que, en general, hablar del método de Newton en problemas de optimización significa su modificación: el método de Newton amortiguado, en el que la secuencia de aproximaciones se construye de acuerdo con la regla

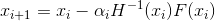
- Método amortiguado explícito de Newton

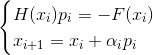
- Método amortiguado implícito de Newton

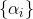
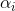
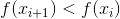
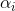
Aquí esta la secuencia es un parámetro del método y su construcción es una tarea separada. En problemas de minimización, natural al elegir habrá un requisito de que, en cada iteración, el valor de la función f disminuya, es decir, . Surge una pregunta lógica: ¿existe tal (positivo) ? Y si la respuesta a esta pregunta es positiva, entonces llamado la dirección de descenso. Entonces la pregunta puede plantearse de esta manera:
¿Cuándo es la dirección generada por el método de Newton la dirección de descenso?
Y para responderlo, tendrá que mirar el problema de minimización desde otro lado.

Métodos de descenso

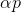
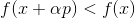
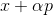
Para el problema de minimización, este enfoque parece bastante natural: a partir de algún punto arbitrario, elegimos la dirección p de alguna manera y damos un paso en esa dirección. . Si entonces toma como un nuevo punto de partida y repita el procedimiento. Si la dirección se elige arbitrariamente, dicho método a veces se denomina método de caminata aleatoria. Es posible tomar vectores base unitarios como una dirección, es decir, dar un paso en una sola coordenada, este método se llama método de descenso de coordenadas. No hace falta decir que son ineficaces? Para que este enfoque funcione bien, necesitamos algunas garantías adicionales. Para hacer esto, presentamos una función auxiliar . 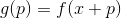Creo que es obvio que la minimización completamente equivalente a minimizar . Si entonces diferenciable puede ser representado como



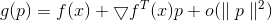
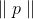
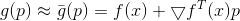
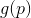
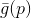
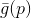
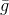
y si lo suficientemente pequeño entonces . Ahora podemos intentar reemplazar el problema de minimización la tarea de minimizar su aproximación (o modelo ) . Por cierto, todos los métodos basados ​​en el uso del modelo llamado gradiente Pero el problema es que Es una función lineal y, por lo tanto, no tiene un mínimo. Para resolver este problema, agregamos una restricción en la longitud del paso que queremos dar. En este caso, este es un requisito completamente natural, porque nuestro modelo describe más o menos correctamente la función objetivo solo en un vecindario lo suficientemente pequeño. Como resultado, obtenemos un problema adicional de optimización condicional:



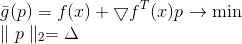
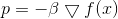
Esta tarea tiene una solución obvia: donde - factor que garantiza el cumplimiento de la restricción. Luego, las iteraciones del método de descenso toman la forma

,

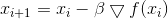
en el que aprendemos el conocido método de descenso de gradiente . Parámetro , que generalmente se denomina velocidad de descenso, ahora ha adquirido un significado comprensible, y su valor se determina a partir de la condición de que el nuevo punto se encuentre en una esfera de un radio dado, circunscrito alrededor del punto anterior.

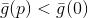
Con base en las propiedades del modelo construido de la función objetivo, podemos argumentar que existe tal , incluso si es muy pequeño, ¿y si entonces . Es de destacar que, en este caso, la dirección en la que nos moveremos no depende del tamaño del radio de esta esfera. Entonces podemos elegir una de las siguientes formas:

1. Seleccione de acuerdo con algún método el valor .
2. Establecer la tarea de elegir el valor apropiado , proporcionando una disminución en el valor de la función objetivo.

El primer enfoque es típico para los métodos de la región de confianza , el segundo conduce a la formulación del problema auxiliar del llamado búsqueda lineal (LineSearch) . En este caso particular, las diferencias entre estos enfoques son pequeñas y no las consideraremos. En cambio, preste atención a lo siguiente:

¿por qué, de hecho, estamos buscando una compensación acostado exactamente en la esfera?

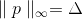
De hecho, podríamos reemplazar esta restricción con el requisito, por ejemplo, que p pertenezca a la superficie del cubo, es decir, (en este caso, no es demasiado razonable, pero ¿por qué no?) o alguna superficie elíptica? Esto ya parece bastante lógico, si recordamos los problemas que surgen al minimizar las funciones de barranco. La esencia del problema es que, en algunas líneas de coordenadas, la función cambia mucho más rápido que en otras. Debido a esto, obtenemos que si el incremento debe pertenecer a la esfera, entonces la cantidad en el que se proporciona el "descenso" debe ser muy pequeño. Y esto lleva al hecho de que lograr un mínimo requerirá una gran cantidad de pasos. Pero si, en cambio, tomamos una elipse adecuada como vecindario, entonces este problema mágicamente quedará en nada.

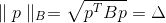
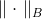
Por la condición de que pertenezcan los puntos de la superficie elíptica, se puede escribir como donde Es una matriz definida positiva, también llamada métrica. Norma llamada la norma elíptica inducida por la matriz . ¿Qué tipo de matriz es esta y de dónde obtenerla? Consideraremos más adelante, y ahora llegamos a una nueva tarea.



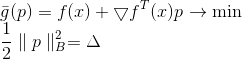
El cuadrado de la norma y el factor 1/2 están aquí únicamente por conveniencia, para no interferir con las raíces. Aplicando el método multiplicador de Lagrange, obtenemos el problema de la optimización incondicional.



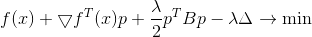
Una condición necesaria para un mínimo para ello es

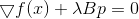
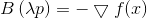
o de donde







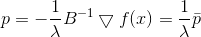
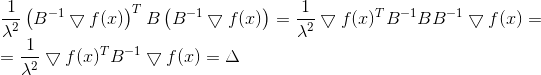
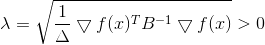
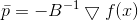
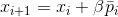
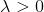
De nuevo vemos que la dirección , en el que nos moveremos, no depende del valor - solo de la matriz . Y de nuevo, podemos recoger eso está plagado de la necesidad de calcular y la inversión explícita de la matriz o resolver el problema auxiliar de encontrar un sesgo adecuado . Desde , se garantiza que la solución a este problema auxiliar existe.

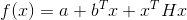
Entonces, ¿qué debería ser para la matriz B? Nos restringimos a las ideas especulativas. Si la función objetivo - cuadrático, es decir, tiene la forma donde positiva definida, es obvio que el mejor candidato para el papel de la matriz es arpillera , ya que en este caso se requiere una iteración del método de descenso que hemos construido. Si H no es definitivo positivo, entonces no puede ser una métrica, y las iteraciones construidas con él son iteraciones del método de Newton amortiguado, pero no son iteraciones del método de descenso. Finalmente, podemos dar una respuesta rigurosa a

Pregunta: ¿La matriz de Hesse en el método de Newton tiene que ser positiva definida?
Respuesta: no, no se requiere ni en el método estándar ni en el método de Newton amortiguado. Pero si se cumple esta condición, entonces el método de Newton amortiguado es un método de descenso y tiene la propiedad de convergencia global y no solo local.

A modo de ilustración, veamos cómo se ven las regiones de confianza al minimizar la conocida función de Rosenbrock utilizando el descenso de gradiente y los métodos de Newton, y cómo la forma de las regiones afecta la convergencia del proceso.



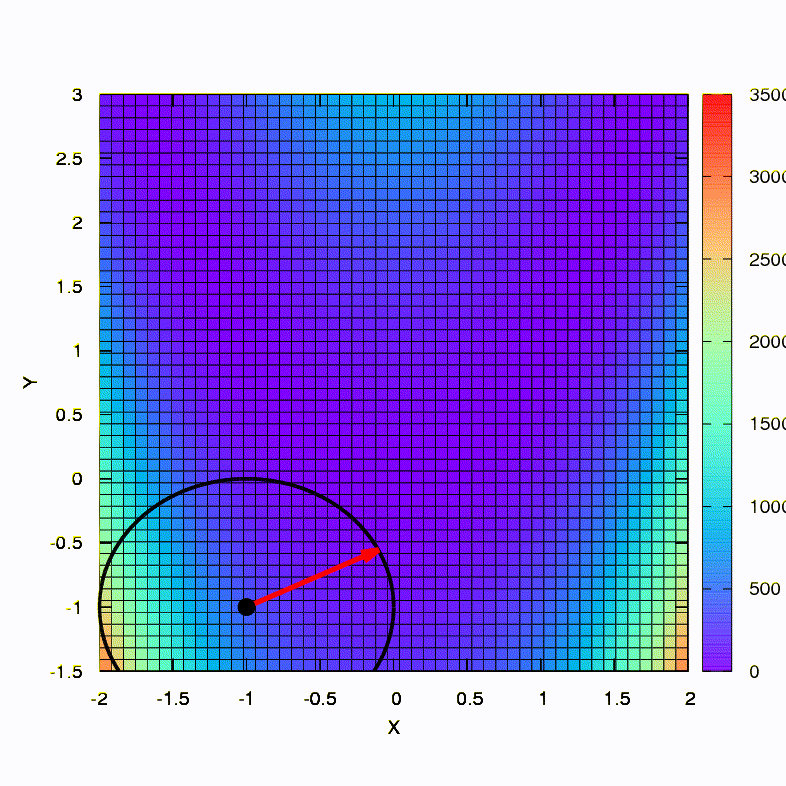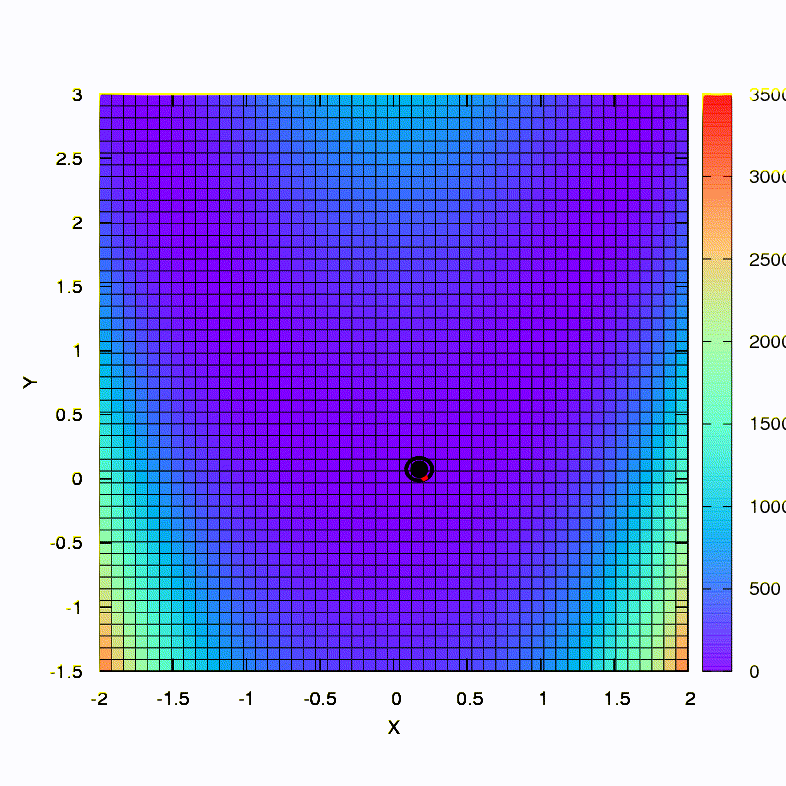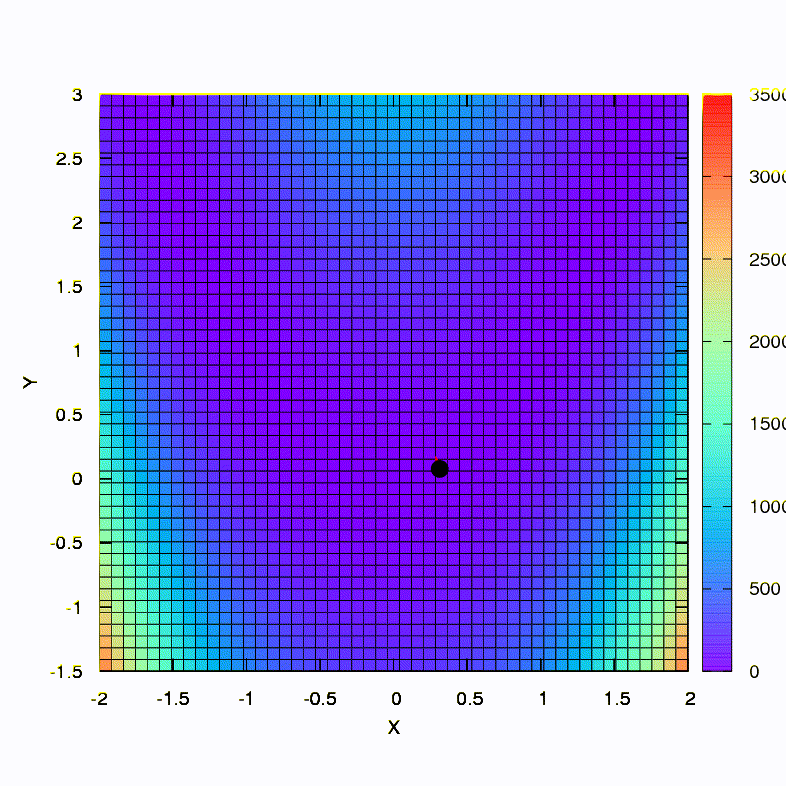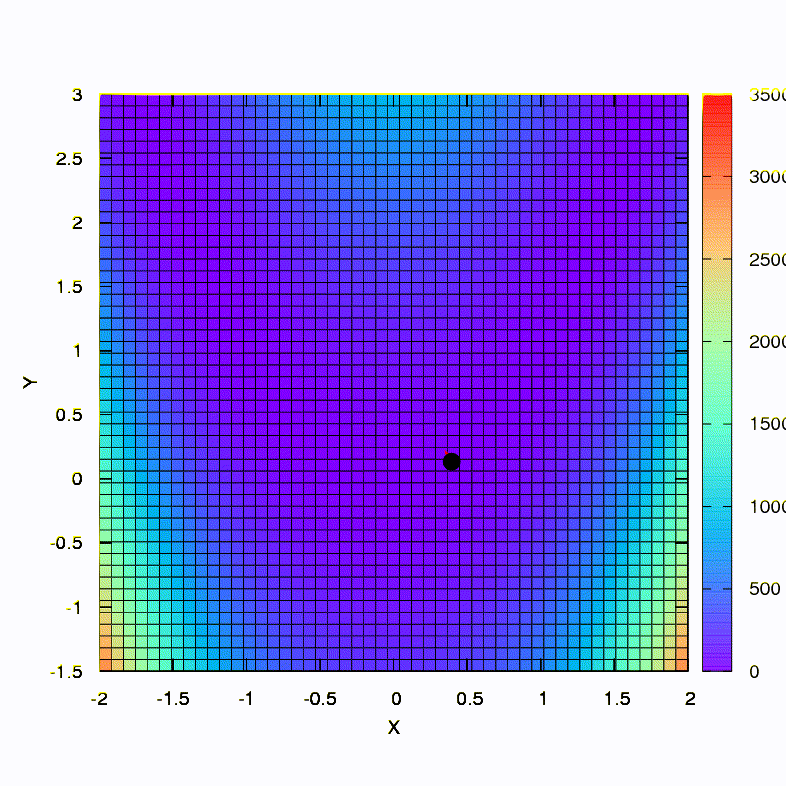
Así es como el método de descenso se comporta con una región de confianza esférica, también es un descenso de gradiente. Todo es como un libro de texto: estamos atrapados en un cañón.



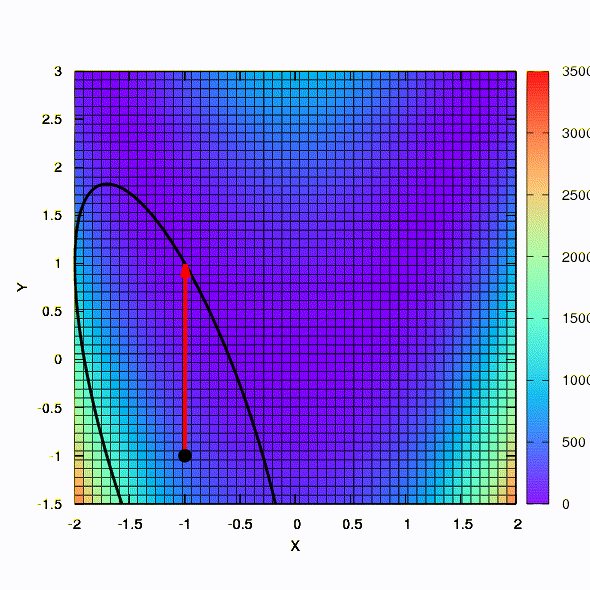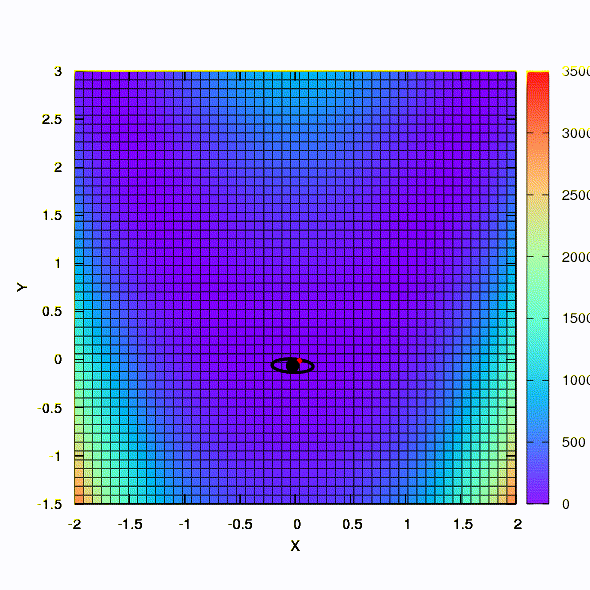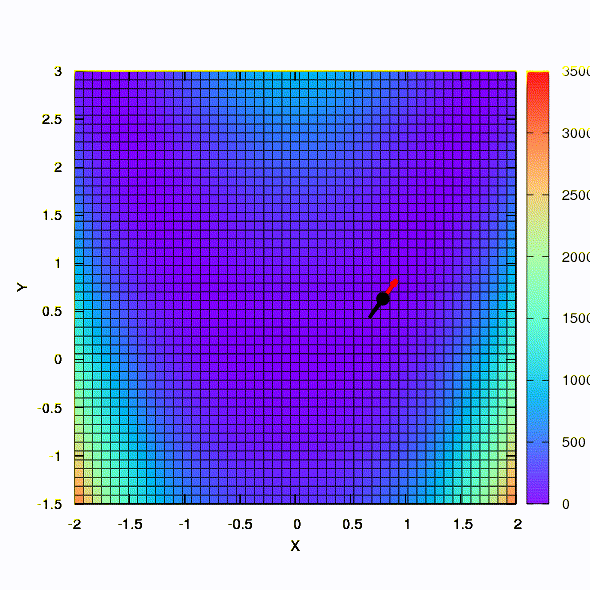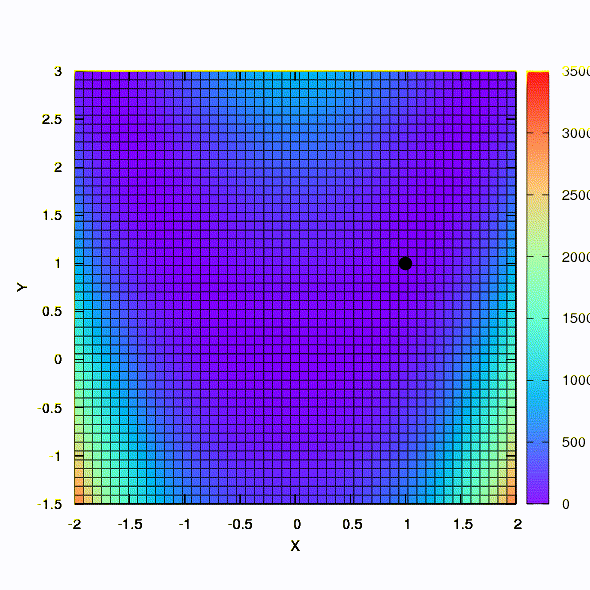
Y esto lo obtenemos si la región de confianza tiene la forma de una elipse definida por la matriz de Hesse. Esto no es más que una iteración del método de Newton amortiguado.

Solo queda por resolver la cuestión de qué hacer si la matriz de Hesse no es definitiva. Hay muchas opciones El primero es anotar. Tal vez tengas suerte y las iteraciones de Newton converjan sin esta propiedad. Esto es bastante real, especialmente en las etapas finales del proceso de minimización, cuando ya está lo suficientemente cerca de una solución. En este caso, las iteraciones del método estándar de Newton se pueden usar sin molestarse con la búsqueda de un vecindario admisible para el descenso. 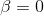O utilice iteraciones del método de Newton amortiguado en el caso de , es decir, en el caso de que la dirección obtenida no sea la dirección de descenso, cámbiela, por ejemplo, a un anti-gradiente. ¡Simplemente no tiene que verificar explícitamente si el Hessian es positivo definido de acuerdo con el criterio de Sylvester , como se hizo aquí! . Es derrochador y sin sentido.
Los métodos más sutiles implican la construcción de una matriz, en un sentido cercano a la matriz de Hesse, pero que posee la propiedad de definición positiva, en particular, corrigiendo valores propios. Un tema separado son los métodos cuasi-newtonianos, o métodos métricos variables, que garantizan la definición positiva de la matriz B y no requieren el cálculo de las segundas derivadas. En general, una discusión detallada de estos temas va mucho más allá del alcance de este artículo.

Sí, y por cierto, se deduce de lo que se ha dicho que el método amortiguado de Newton con una definición positiva del hessiano es un método de gradiente . Así como los métodos cuasi-newtonianos. Y muchos otros, basados ​​en una elección separada de dirección y tamaño de paso. Por lo tanto, contrastar el método de Newton con la terminología de gradiente es incorrecto.

Para resumir

El método de Newton, que a menudo se recuerda cuando se discuten los métodos de minimización, generalmente no es el método de Newton en su sentido clásico, sino el método de descenso con la métrica especificada por el hessiano de la función objetivo. Y sí, converge globalmente si el hessiano es positivo en todas partes. Esto es posible solo para funciones convexas, que son mucho menos comunes en la práctica de lo que nos gustaría, por lo que, en el caso general, sin las modificaciones apropiadas, la aplicación del método de Newton (no nos separaremos del colectivo y continuaremos llamándolo así) no garantiza el resultado correcto. El aprendizaje de redes neuronales, incluso las superficiales, generalmente conduce a problemas de optimización no convexos con muchos mínimos locales. Y aquí hay una nueva emboscada. El método de Newton generalmente converge (si converge) rápidamente. Me refiero a muy rápido. Y esto, curiosamente, es malo, porque llegamos a un mínimo local en varias iteraciones. Y para funciones con terreno complejo puede ser mucho peor que el global. El descenso de gradiente con búsqueda lineal converge mucho más lentamente, pero es más probable que se "salte" las crestas de la función objetivo, lo cual es muy importante en las primeras etapas de minimización. Si ya ha reducido bien el valor de la función objetivo, y la convergencia del descenso del gradiente ha disminuido significativamente, entonces un cambio en la métrica puede acelerar el proceso, pero esto es para las etapas finales.

Por supuesto, este argumento no es universal, no es indiscutible y, en algunos casos, incluso incorrecto. Además de la afirmación de que los métodos de gradiente funcionan mejor en los problemas de aprendizaje.