Laboratorio interactivo de termodinámica como medio eficaz de entrenamiento en simulación.

Introduccion

La capacitación en simulación con recursos educativos multimedia es una de las áreas prometedoras de informatización de la educación moderna. Por entrenamiento de simulación nos referiremos a un modelo de entrenamiento en el que los procesos físicos y las condiciones similares a las reales, pero que tienen una serie de cualidades idealizadas, se reproducen virtualmente utilizando software. La posibilidad de interacción interactiva con un modelo virtual de un proceso físico particular puede reducir significativamente el nivel de abstracción del conocimiento sobre este proceso, resultando en una mayor eficiencia de obtención y asimilación de este conocimiento por parte de una persona [1] .

Objeto de estudio y planteamiento del problema.

Como objeto de estudio, consideramos una de las ramas más importantes de la física general: la termodinámica clásica. En el contexto de las actividades educativas, el conocimiento en esta disciplina se enseña en varias formas, los principales son: material teórico consolidado en forma de conferencias y libros de texto; tareas prácticas en forma de colecciones de tareas y pruebas; Taller de laboratorio en forma de directrices para la implementación de experimentos de laboratorio sobre los temas de la teoría básica. Las formas de enseñanza enumeradas difieren en el nivel de abstracción de la información transmitida, y juntas forman la imagen más completa del conocimiento en la disciplina que se estudia.

La forma de conocimiento más exigente en términos de metodología e implementación técnica es un taller de laboratorio. Para este propósito, se crean laboratorios de capacitación especialmente equipados que cumplen con los requisitos del proceso educativo en las universidades y colegios. El acceso oportuno a estos laboratorios, por regla general, se lleva a cabo en el proceso de los estudiantes que pasan la capacitación a tiempo completo. La capacidad de trabajar en laboratorios educativos está indisolublemente ligada a la necesidad de la presencia física del estudiante en el laboratorio, así como al alto costo de mantener y mantener el laboratorio en condiciones de su operación intensiva.

Cuando un estudiante se somete a un aprendizaje a distancia o fuera de línea sin la ayuda de una organización educativa, la capacidad de realizar experimentos de laboratorio a menudo está completamente ausente. Como muestra la práctica, en este caso, el estudiante se familiariza con los experimentos de laboratorio a través de videos o animaciones que se encuentran (si es posible) en el dominio público de Internet, que es una forma ineficaz de estudiar el material educativo requerido debido a la falta de interactividad y estructura del material, y a menudo restricciones de idioma y baja Calidad del material presentado.

En vista de lo anterior, una tarea urgente para los desarrolladores de recursos educativos multimedia es la creación de una herramienta de aprendizaje que brinde al proceso educativo todas las funciones necesarias en términos de realizar trabajos experimentales, contenga material metodológico estructurado y contribuya a la asimilación efectiva del conocimiento en un campo de estudio particular. En el aspecto técnico, esta herramienta de capacitación debe tener la flexibilidad para integrarse en varios sistemas de aprendizaje a distancia (en forma de aplicaciones web y componentes de software), la capacidad de ejecutarse en dispositivos móviles y computadoras personales, alto rendimiento y facilidad de administración.

Un ejemplo de implementación de un modelo de simulación de un experimento de laboratorio.

Considere el experimento de laboratorio "Gases reales y el punto de transición de fase" del curso de termodinámica para estudiantes y estudiantes mayores de escuelas secundarias. El propósito de este experimento es cuantificar el gas real (hexafluoruro de azufre SF6) y determinar su punto de transición de fase. La experiencia de laboratorio se realiza en una configuración de laboratorio (Figura 1) fabricada por 3B Scientific [2] .


Figura 1 - Apariencia de un análogo natural de una configuración de laboratorio para determinar el punto de transición de fase de un gas real

La configuración de laboratorio presentada está equipada con un tanque de gas, un medidor para medir la presión del gas en el tanque, un pistón móvil con un mecanismo de tornillo y una escala, un sistema de válvula y un termómetro electrónico para medir la temperatura del gas. La rotación del volante desplaza el pistón, que a su vez cambia el volumen libre del depósito de gas. La parte de trabajo del depósito de gas está hecha de material translúcido, lo que le permite observar visualmente el estado de la sustancia de prueba durante el experimento.

El punto de transición de fase de un gas real se caracteriza por la temperatura crítica, la presión crítica y la densidad crítica. Por debajo de la temperatura crítica, la sustancia está en estado gaseoso a grandes volúmenes y en estado líquido a pequeños volúmenes. A volúmenes intermedios, puede existir como una mezcla de líquido y gas, en el que un cambio en el volumen en condiciones isotérmicas provoca un cambio en el estado de agregación: la fracción gaseosa aumenta al aumentar el volumen y la presión de la mezcla permanece constante. Dado que los líquidos y los vapores tienen diferentes densidades, están separados en el campo gravitacional. A medida que aumenta la temperatura, la densidad del líquido disminuye y la densidad del gas aumenta hasta que estas dos densidades se vuelven iguales al mismo valor de densidad crítica. Por encima de la temperatura crítica, el gas no puede convertirse a un estado líquido. Sin embargo, en condiciones isotérmicas, el gas no obedece las leyes de un gas ideal hasta que su temperatura haya aumentado significativamente por encima de la temperatura crítica.

El estado del gas, dependiendo de los parámetros de presión (P), volumen (V) y temperatura (T), se representa utilizando el diagrama de fase de Clapeyron. Como base matemática del experimento, se utiliza el modelo de gas de van der Waals:

$$

$$Pr (Vr) = 8Tr / (3Vr-1) -3 / Vr ^ 2$$

donde Pr es la presión de gas reducida igual a la relación de su presión real a la presión en el punto crítico (Pr = P / Pc); Vr es el volumen de gas reducido igual a la relación de su volumen real al volumen en el punto crítico (Vr = V / Vc); Tr es la temperatura reducida del gas igual a la relación entre su temperatura real y la temperatura en el punto crítico (Tr = T / Tc).

La ecuación de van der Waals permite calcular isotermas (líneas de igual temperatura) para el gas de prueba en la forma dada (Figura 2).

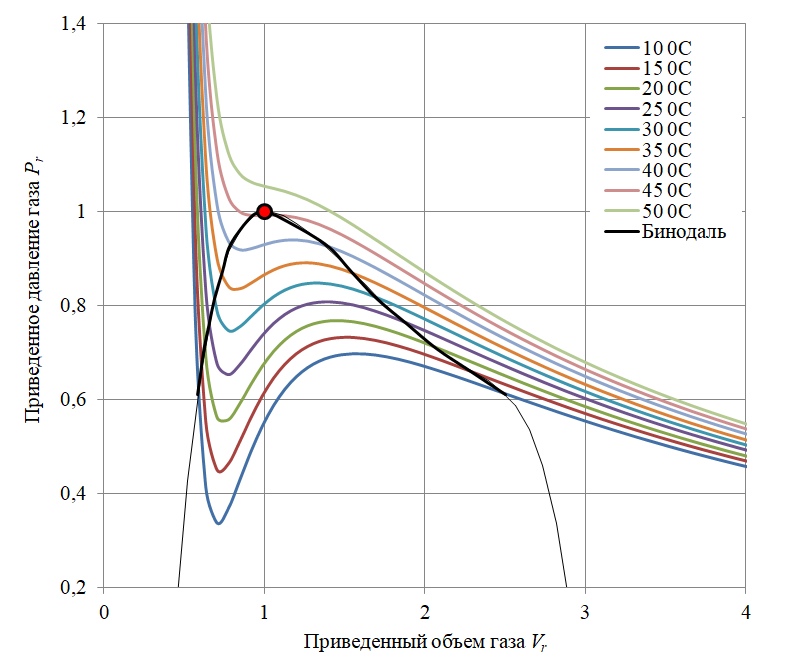Figura 2 - Diagrama de fase de Clapeyron para hexafluoruro de azufre SF6 excluyendo el equilibrio vapor-líquido

Como se puede ver en el diagrama de la Figura 2, a una temperatura de gas por debajo de la temperatura crítica (Tc), la ecuación de van der Waals en esa parte de la isoterma donde dPr / dVr> 0 tiene un carácter oscilatorio. En estas áreas, la sustancia tiene la forma de una mezcla de gas y líquido, y en realidad, la condensación de gas se produce a lo largo del camino isobárico (el volumen cambia a presión constante). Por lo tanto, el diagrama de van der Waals dentro de la llamada curva binodal (curva negra en el diagrama) [3] describe inadecuadamente el comportamiento de un gas real.

Para resolver este problema, se utilizó el método Maxwell de áreas iguales [4] , cuya esencia es reemplazar la sección isotérmica oscilante con una línea horizontal (isobar) que divide el área descrita por la isoterma en dos áreas de igual tamaño (Figura 3).

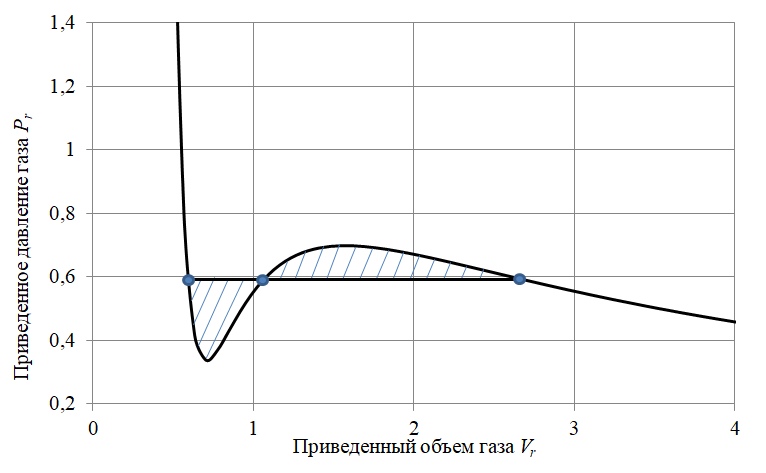Figura 3 - Al método de áreas iguales de Maxwell

A continuación se muestra un fragmento de código (Matlab) para resolver el problema descrito [4].

function maxwell_equal_area_2 clc; clear all; close all %  Tr  Tc: Tr = T/Tc Tr = 0.9; %    Pr (  --) Prfh = @(Vr) 8/3*Tr./(Vr - 1/3) - 3./(Vr.^2); %    Vr = linspace(0.5,4,100); %    Pr = Prfh(Vr); 

Para calcular las áreas de dos regiones formadas por la isoterma y la isobara, es necesario encontrar las tres raíces de la ecuación polinómica:

$$

$$Vr ^ 3- (1 + 8Tr / Pr) / 3 + 3 / Pr-1 / Pr = 0$$

 %    vdWp = [1 -1/3*(1+8*Tr/y) 3/y -1/y]; %     v = sort(roots(vdWp)) %  A1 (       ) A1 = (v(2)-v(1))*y - quad(Prfh,v(1),v(2)) %  A2 (       ) A2 = quad(Prfh,v(2),v(3)) - (v(3)-v(2))*y % ,  ,  ,  A1=A2 Pr_equal_area = fzero(@equalArea, 0.65) 

Los resultados de los cálculos se pueden mostrar en el diagrama (Figura 4).

 xx = [v(1) Vr(Vr >= v(1) & Vr <= v(2)) v(2)]; yy = [Prfh(v(1)) Pr(Vr >= v(1) & Vr <= v(2)) Prfh(v(2))]; lightgray = [0.9 0.9 0.9]; fill(xx,yy,lightgray) xx = [v(2) Vr(Vr >= v(2) & Vr <= v(3)) v(3)]; yy = [Prfh(v(2)) Pr(Vr >= v(2) & Vr <= v(3)) Prfh(v(3))]; fill(xx,yy,lightgray) %      text(v(1),1,sprintf('A1 = %f',A1)) text(v(3),1,sprintf('A2 = %f',A2)) 

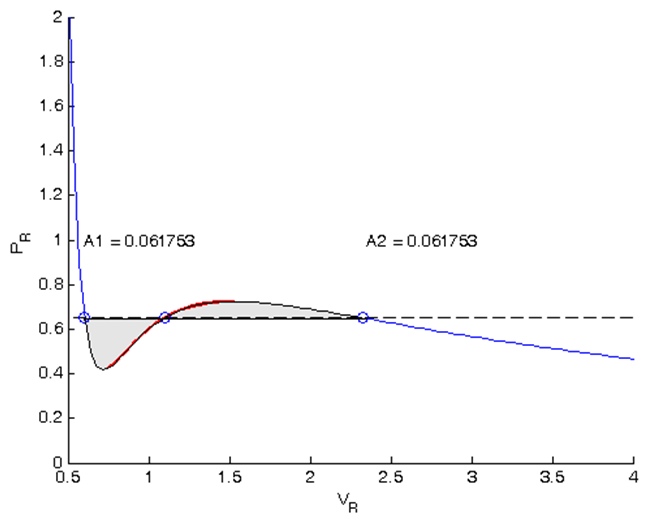Figura 4 - Resultados del cálculo de isobaras por el método de áreas iguales de Maxwell en Matlab

La forma final de la función para el método de área igual:

 function Z = equalArea(y) Tr = 0.9; vdWp = [1 -1/3*(1+8*Tr/y) 3/y -1/y]; v = sort(roots(vdWp)); Prfh = @(Vr) 8/3*Tr./(Vr - 1/3) - 3./(Vr.^2); A1 = (v(2)-v(1))*y - quad(Prfh,v(1),v(2)); A2 = quad(Prfh,v(2),v(3)) - (v(3)-v(2))*y; Z = A1 - A2; % :  ; :  

Por lo tanto, el modelo matemático final del experimento está representado por el diagrama de Clapeyron para el hexafluoruro de azufre, teniendo en cuenta las condiciones de equilibrio vapor-líquido (Figura 5).


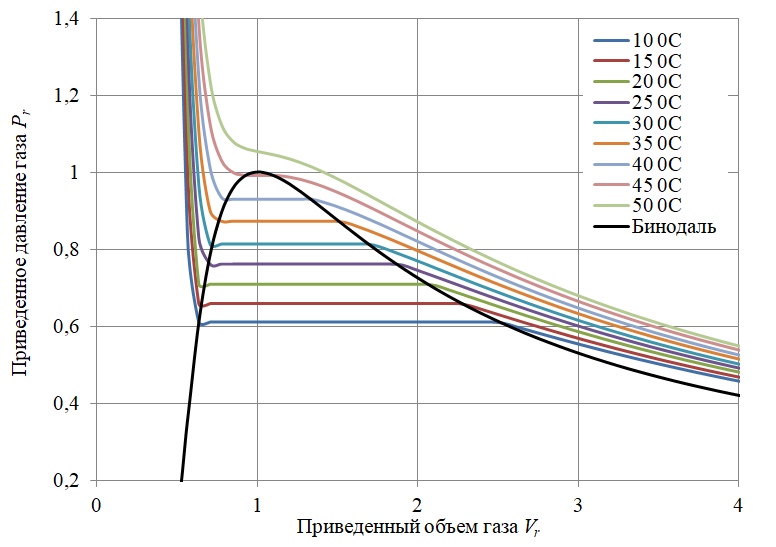Figura 5 - Diagrama de fase de Clapeyron para hexafluoruro de azufre SF6 teniendo en cuenta el equilibrio vapor-líquido

Junto con el componente matemático, el modelo de simulación del experimento incluye un conjunto de objetos gráficos que reflejan visualmente el equipo de laboratorio (Figura 6).


Figura 6 - Modelo gráfico de una configuración de laboratorio: 1 - manómetro; 2 - termostato de circulación; 3 - termómetro electrónico; 4 - tanque de gas; 5 - mecanismo de control de volumen; 6 - válvula de llenado de gas

Los errores generados dinámicamente que simulan procesos transitorios (inestables), inexactitudes de medición, sensibilidad de los controles, etc. se agregan a los valores medidos en el modo de ejecución del experimento. El modelo de simulación proporciona completamente la observación del proceso físico con la posibilidad de cambiar los parámetros de entrada y las condiciones experimentales.

Un ejemplo de implementación de un taller de laboratorio virtual.

Basado en el ejemplo de la metodología para calcular modelos de simulación de procesos físicos descritos anteriormente, utilizando el lenguaje de programación de alto nivel AppGameKit , se ha desarrollado un taller de laboratorio interactivo de termodinámica clásica, que cubre los temas principales del curso: energía interna, leyes de gases, transferencia de calor, expansión térmica, ciclos termodinámicos. Este desarrollo está destinado a experimentos de laboratorio en ausencia de equipos de laboratorio reales. Las instalaciones de laboratorio se realizan de acuerdo con sus homólogos reales. Cada trabajo de laboratorio incluye pautas breves e información de referencia necesaria para procesar datos experimentales.

Una característica distintiva del laboratorio virtual es su flexibilidad complementaria debido al soporte multiplataforma. El trabajo de laboratorio de simulación es posible en computadoras personales, dispositivos móviles y en un entorno de navegador web (sin la necesidad de instalar software en el dispositivo de un usuario). La solución presentada utiliza un algoritmo único para cargar una escena gráfica en 3D en la memoria utilizando su propio formato de datos binarios, lo que permite reducir el tiempo de reconstrucción de modelos 3D en el motor del juego a varios segundos, lo cual es un factor importante cuando se ejecuta el programa en dispositivos móviles.

La Figura 7 muestra una captura de pantalla que muestra el laboratorio virtual que se ejecuta en el navegador web Microsoft Edge, que proporciona soporte completo de hardware para gráficos 3D basados ​​en el estándar HTML5 y la tecnología WebGL.


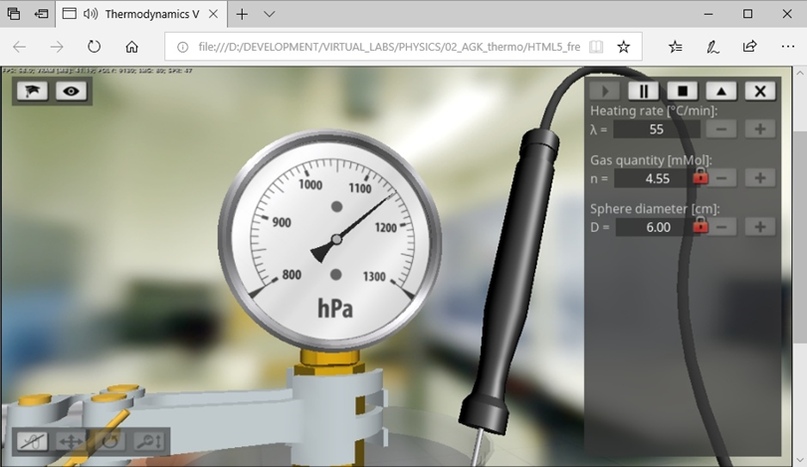Figura 7 - Ejecución de un laboratorio virtual en un navegador web Microsoft Edge

A continuación se muestran las versiones en línea del trabajo de laboratorio, para las cuales se recomienda utilizar el navegador web Microsoft Edge, que forma parte del sistema operativo Microsoft Windows 10:

1. Energía interna y trabajo mecánico.
2. Energía interna y corriente eléctrica.
3. Ley de Boyle-Marriott
4. Ley de Lussac Gay
5. Adiabat aéreo
6. Gases reales y punto de transición de fase
7. Leslie Cube
8. Conductividad térmica
9. Expansión térmica de sólidos.
10. Anomalía del agua
11. Motor Stirling Modelo D
12. Motor Stirling Modelo G
13. Bombas de calor

Para realizar el trabajo de laboratorio en un dispositivo móvil (teléfono inteligente o tableta) basado en el sistema operativo Android, puede descargar la aplicación móvil del laboratorio virtual.

Conclusión

El ejemplo de la implementación de la herramienta de capacitación en simulación descrita en este artículo basada en el laboratorio virtual de termodinámica demuestra la posibilidad de complementar el proceso educativo con una herramienta metodológica auxiliar que cumpla con los requisitos y estándares de la educación general y superior moderna. El concepto generalizado de desarrollar recursos educativos multimedia incluye una serie de etapas principales: determinar el componente metodológico real del taller de laboratorio (incluida la elección de equipos de laboratorio eficaces y su referencia y apoyo metodológico); desarrollo de un modelo numérico de simulación del experimento; implementación del componente gráfico de un taller de laboratorio de simulación; implementación del componente de software de un taller de laboratorio de simulación; integración de un taller de laboratorio de simulación en el proceso educativo (introducción del desarrollo en un curso de capacitación existente o la creación de un nuevo curso de capacitación enfocado en trabajar con un taller de laboratorio de simulación).

Una de las áreas prometedoras de desarrollo de la tecnología de educación de simulación en este momento es la implementación de sistemas de capacitación de múltiples agentes, cuyo trabajo se basa en los algoritmos para generar caminos educativos individuales con la formación dinámica de contenido educativo. Dichos sistemas proporcionan un entorno adaptativo del entorno de aprendizaje, teniendo en cuenta las características individuales del perfil del usuario. Estos algoritmos le permitirán obtener: para los estudiantes: un plan personalizado, contenido, metodología y herramientas de aprendizaje electrónico; para profesores: tecnologías innovadoras de enseñanza y análisis de competencias formadas, para escuelas y universidades, un modelo moderno de gestión de procesos educativos.

Referencias bibliográficas

1. Laboratorios virtuales y simulaciones técnicas
2. Equipamiento de laboratorio 3B Scientific
3. Método para calcular curvas binodales
4. Método de área igual para la ecuación de Van der Waals