El artículo discutirá la experiencia de desarrollar un programa para crear una cartera de bonos efectiva en términos de minimizar su duración . Quizás no sea original y para todos los que inviertan en bonos, los problemas para determinar los pesos óptimos se han resuelto por mucho tiempo, pero aun así, espero que el enfoque descrito y el código del programa proporcionado sean útiles para alguien.

El artículo, debido a la presencia de una pequeña cantidad de matemáticas en él, puede parecer complicado para alguien. Pero si ya ha decidido comenzar a invertir, debe estar preparado para el hecho de que las matemáticas a menudo se encuentran en la realidad financiera y son aún más complicadas.

El código fuente del programa y un portafolio de ejemplo para la optimización están disponibles en GitHub.

ACTUALIZACIÓN: Como se prometió, hizo un servicio web simple que hace que el programa esté disponible para todos sin copiar ni compilar código.
el enlace
Instrucciones de uso en el mismo lugar.
Si algo no funciona o necesita arreglar algo, escriba los comentarios.

Entonces, tenemos la tarea de formar una cartera efectiva de bonos.

Parte 1. Determinación de la duración de la cartera.

Desde el punto de vista de minimizar los riesgos no sistémicos (para los cuales la cartera está diversificada), la elección de los valores se llevó a cabo considerando los parámetros de una emisión en particular, el emisor (si no se limita a OFZ ), el comportamiento en papel, etc. (los enfoques para dicho análisis son bastante individuales para cada inversor y no se consideran en este artículo).

Habiendo seleccionado varios valores que son los más preferibles para la inversión, surge una pregunta natural: ¿cuántos bonos de cada emisión necesita comprar? Esta es la tarea de optimizar la cartera para que los riesgos de la cartera sean mínimos.

Es natural considerar la duración como un parámetro optimizado. Por lo tanto, la tarea es determinar el peso de los valores en la cartera, de modo que la duración de la cartera sea mínima para un rendimiento fijo de la cartera. Aquí debe hacer algunas reservas:

1. La duración de la cartera de bonos está determinada por sus valores constitutivos. Estas duraciones son conocidas (son de dominio público). La duración de la cartera no es igual a la duración máxima de los valores incluidos en ella (existe tal falacia). La relación entre la duración de los valores individuales y la duración de toda la cartera no es lineal, es decir. no es igual a la duración promedio ponderada de sus enlaces constituyentes (para verificar esto, es suficiente considerar la fórmula de duración (ver (1) a continuación) e intentar calcular la duración promedio ponderada de una cartera condicional que consiste, por ejemplo, en dos documentos. Sustituyendo la fórmula por la duración en tal expresión de cada trabajo, en la salida no obtenemos una fórmula para la duración de la cartera, sino una especie de "tontería", con dos tasas de descuento y flujos de efectivo inconsistentes como ponderaciones).
2. A diferencia de la duración, el rendimiento de la cartera depende de los rendimientos de los instrumentos incluidos en él linealmente. Es decir Al colocar dinero en varios instrumentos con un ingreso fijo, obtendremos un rendimiento directamente proporcional al volumen de inversiones en cada instrumento (y esto funciona para una tasa compleja, y no solo para una simple). Asegúrate de que esto sea aún más fácil.
3. El rendimiento al vencimiento ( YTM ) se usa como la tasa de rendimiento del bono. Generalmente se usa para calcular la duración. Sin embargo, el rendimiento al vencimiento de toda la cartera aquí es bastante arbitrario, ya que El vencimiento de todos los valores es diferente. Al formar una cartera, esta característica debe tenerse en cuenta en el sentido de que la cartera debe revisarse, no menos que las herramientas de las que está compuesta, salgan de circulación.

Entonces, la primera tarea es el cálculo correcto de la duración de la cartera en sí. La forma inmediata de hacer esto es: determinar todos los pagos de la cartera, calcular el rendimiento al vencimiento, descontar los pagos, multiplicar los valores recibidos por los términos de estos pagos y sumarlos. Para hacer esto, debe combinar los calendarios de pago de todos los instrumentos en un solo calendario de pagos para toda la cartera, componer una expresión para calcular el rendimiento al vencimiento, calcularlo, descontarlo para cada pago, multiplicarlo por su fecha de vencimiento, agregar ... En general, una pesadilla. Hacer esto incluso para dos trabajos es una tarea muy laboriosa, sin mencionar que recalcula regularmente la cartera en el futuro. De esta manera no nos conviene.

Por lo tanto, es necesario buscar una oportunidad para determinar la duración de la cartera de una manera diferente y más rápida. Una opción aceptable sería aquella que le permite determinar la duración de la cartera por las duraciones de los instrumentos conocidos. Los estudios de la fórmula de duración han demostrado que existe ese camino y aquí me gustaría darlo en detalle (si alguien no está interesado en los detalles matemáticos de los cálculos, puede omitir con seguridad algunos párrafos con las fórmulas e ir directamente al ejemplo).

La duración de un instrumento de deuda se define de la siguiente manera:

$$$$ display $$ \ begin {ecation} D = \ frac {\ sum_ {i} PV_i \ cdot t_i} {\ sum_ {i} PV_i} ~~~~~~~~~~~~~ (1) \ end {ecuación} $$ display $$

donde:

• t _i - momento de pago del i-ésimo pago;
• $$$ inline $ \ begin {equation} PV_i = \ frac {CF_i} {(1 + r) ^ {t_i}} \ end {ecation} $ inline $ - i-ésimo pago con descuento;
• CF _i - i-ésimo pago;
• r es la tasa de descuento.

Introducimos el coeficiente de descuento k = (1 + r) y consideramos el monto de los pagos con descuento P en función de k :

$$$$ display $$ \ begin {ecation} P (k) = \ sum_ {i} PV_i = \ sum_ {i} {\ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~ ~~~~ (2) \ end {ecuación} $$ display $$

Diferenciando P con respecto a k, obtenemos

$$$$ display $$ \ begin {ecation} P '(k) = - \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i + 1}}} = - \ frac {1} {k} \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~~~~ (3) \ end {ecuación} $$ display $$

Dado lo último, la expresión para la duración del enlace toma la forma

$$$$ display $$ \ begin {ecation} D = -k \ frac {P '(k)} {P (k)} ~~~~~~~~~~~~~ (4) \ end {ecation} $$ display $$

Al mismo tiempo, recordamos que como tasa de descuento r en el caso de un bono, se utiliza el rendimiento al vencimiento (YTM).

La expresión obtenida es válida para un enlace, pero estamos interesados ​​en una cartera de bonos. Pasemos a determinar la duración de la cartera.

Presentamos la siguiente notación:

• P _i es el precio del i-ésimo bono;
• z _i - el número de valores del i-ésimo bono en la cartera;
• k _i - coeficiente de descuento del bono i-ésimo en la cartera;
• $$$ inline $ \ begin {equation} P_p = \ sum_ {i} {z_iP_i} \ end {ecation} $ inline $ - precio de cartera;
• $$$ inline $ \ begin {equation} w_i = \ frac {z_iP_i} {\ sum_ {i} z_iP_i} = \ frac {z_iP_i} {P_p} \ end {ecuación} $ inline $ - el peso del bono i-ésimo en la cartera; requisito obvio$$ $ en línea $ \ begin {equation} \ sum_ {i} w_i = 1 \ end {equation} $ en línea $ ;
• $$$ inline $ \ begin {equation} k_p = \ sum_ {i} w_ik_i \ end {equation} $ inline $ - coeficiente de descuento de cartera;

Debido a la linealidad de la diferenciación, lo siguiente es cierto:

$$$$ display $$ \ begin {ecation} P'_p (k) = \ left (\ sum_ {i} z_iP_i (k) \ right) '= \ sum_ {i} z_iP'_i (k) ~~~~~ ~~~~~~~~ (5) \ end {ecuación} $$ display $$

Por lo tanto, teniendo en cuenta (4) y (5), la duración de la cartera puede expresarse como

$$$$ display $$ \ begin {ecation} D_p = -k_p \ frac {P'_p} {P_p} = - \ sum_ {i} w_ik_i \ left (\ frac {\ sum_ {j} z_jP'_j} {\ sum_ {j} z_jP_j} \ right) ~~~~~~~~~~~~~~ (6) \ end {ecuación} $$ display $$

De (4) se sigue inequívocamente$$ $ inline $ \ begin {equation} P'_j = - \ frac {D_jP_j} {k_j} \ end {ecation} $ inline $ .
Sustituyendo esta expresión en (6), llegamos a la siguiente fórmula para la duración de la cartera:

$$$$ display $$ \ begin {ecation} D_p = \ sum_ {i} w_ik_i \ left (\ frac {\ sum_ {j} \ frac {D_j} {k_j} z_jP_j} {\ sum_ {j} z_jP_j} \ right) = \ left (\ sum_ {i} w_ik_i \ right) \ left (\ sum_ {j} w_j \ frac {D_j} {k_j} \ right) ~~~~~~~~~~~~~ (7) \ end {ecuación} $$ display $$

En las condiciones en que se conoce la duración y el rendimiento al vencimiento de cada instrumento (y recordamos que estamos en esas condiciones), la expresión (7) es la fórmula deseada para determinar la duración de una cartera en función de la duración de sus bonos. Solo parece complicado en apariencia, pero de hecho ya está listo para su uso práctico con la ayuda de las funciones más simples de MS Excel, que ahora haremos con un ejemplo.

Ejemplo

Para calcular la duración de la cartera de acuerdo con la fórmula (7), necesitamos datos de entrada que incluyan el conjunto real de valores incluidos en la cartera, sus duraciones y rendimiento al vencimiento. Como se mencionó anteriormente, esta información está disponible públicamente, por ejemplo, en el sitio web rusbonds.ru en la sección análisis de bonos. Los datos de origen se pueden descargar en formato Excel.

Como ejemplo, considere una cartera de valores que consta de 9 bonos. La tabla de datos original descargada de rusbonds tiene el siguiente formulario.



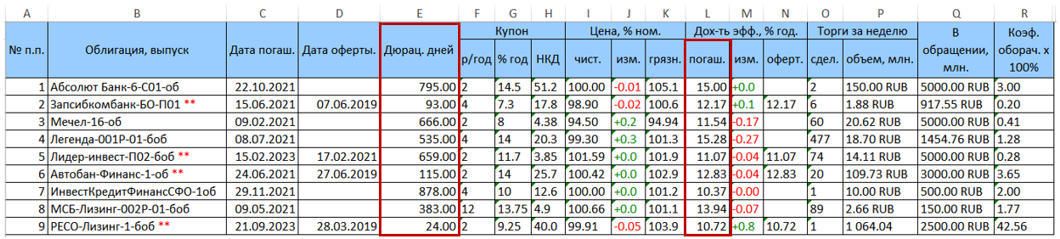
Dos columnas de interés para nosotros con una duración (columna E) y rendimiento al vencimiento (columna L = YTM) están resaltadas en rojo.

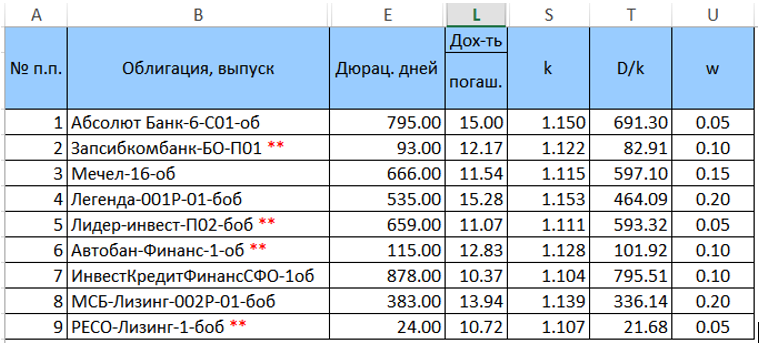
Establecemos pesos w para bonos en esta cartera (hasta ahora de manera arbitraria, pero de modo que su suma sea igual a la unidad) y calculamos k = (1 + YTM / 100) y D / k = ("columna E" / k). La tabla convertida (sin columnas adicionales) se verá como



A continuación, calculamos el producto.$$ $ en línea $ \ begin {ecation} w_j \ frac {D_j} {k_j} \ end {ecation} $ inline $ y$$ $ inline $ \ begin {equation} w_ik_i \ end {equation} $ inline $ y sumarlos, y multiplicar las cantidades resultantes por una por la otra. El resultado de esta multiplicación será la duración deseada para una distribución dada de pesos.



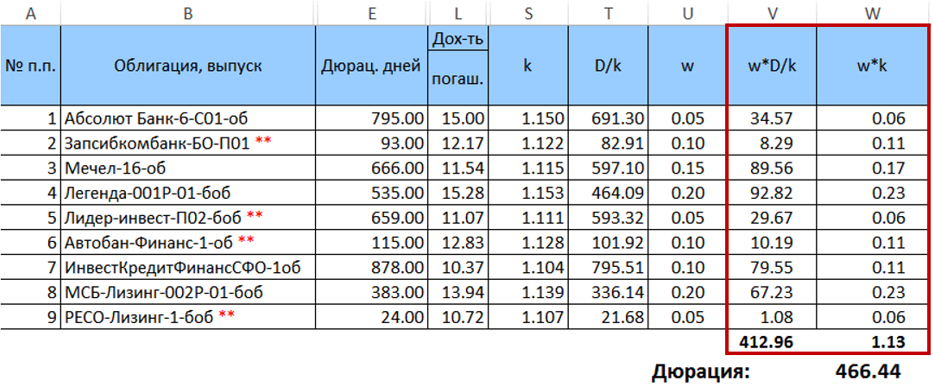
Entonces, la duración deseada de la cartera es de 466.44 días. Es importante tener en cuenta que en este caso particular, la duración calculada por la fórmula (7) es muy ligeramente diferente de la duración promedio ponderada calculada con los mismos pesos (desviación <0.5 días). Sin embargo, esta diferencia aumenta con un aumento en la dispersión de los pesos. También aumentará con un aumento en la extensión de la duración del papel.

Después de haber obtenido la fórmula para calcular la duración de la cartera, el siguiente paso es determinar el peso de los valores para que, con un rendimiento dado, la duración estimada de la cartera sea mínima. Pasamos a la siguiente parte: optimización de cartera.

Parte 2. Optimización de la cartera de bonos

La expresión (7) es una forma cuadrática, con la matriz

$$$$ display $$ \ begin {ecation} A = \ left \ {k_i \ frac {D_j} {k_j} \ right \} = \ begin {pmatrix} D_1 & \ ldots & k_1 \ frac {D_n} {k_n} \ \ \ vdots & D_j & \ vdots \\ k_n \ frac {D_1} {k_1} & \ ldots & D_n \ end {pmatrix} \ end {ecation} $$ display $$

En consecuencia, en forma matricial, la expresión para la duración de la cartera (7) se puede escribir de la siguiente manera:

$$$$ display $$ \ begin {ecation} D_p = w ^ TAw ~~~~~~~~~~~~~ (8) \ end {ecation} $$ display $$

donde w es el vector de columna de los pesos de los bonos en la cartera. Como se mencionó anteriormente, la suma de los elementos del vector w debe ser igual a la unidad. Por otro lado, la expresión $$$k_p = \ sum_ {i} w_i k_i$ (que, en esencia, es un producto escalar simple ( w , k ) , donde k es el vector de los coeficientes de descuento de bonos) debe ser igual a la tasa de descuento objetivo de la cartera y, por lo tanto, debe establecerse el rendimiento de la cartera objetivo.

Por lo tanto, la tarea de optimizar una cartera de bonos es minimizar la función cuadrática (8) con restricciones lineales.

El método clásico para encontrar el extremo condicional de una función de varias variables es el método multiplicador de Lagrange. Sin embargo, este método no es aplicable aquí, aunque solo sea porque la matriz A se degenera por construcción (pero no solo por esto; omitimos los detalles del análisis de la aplicabilidad del método Lagrange aquí para no sobrecargar el artículo con un contenido matemático excesivo).

La imposibilidad de aplicar un método analítico fácil y asequible lleva a la necesidad de utilizar métodos numéricos. El problema de optimizar una función cuadrática es bien conocido y tiene varios algoritmos eficientes desarrollados desde hace mucho tiempo implementados en bibliotecas públicas.

Para resolver este problema en particular, se utilizaron la biblioteca ALGLIB y los algoritmos de optimización cuadrática implementados en ella, QP-Solvers , incluidos en el paquete minqp.

El problema de optimización cuadrática en general es el siguiente:

Es necesario encontrar un vector n-dimensional que minimice la función

$$$$ display $$ \ begin {ecation} F = \ frac {1} {2} w ^ T Qw + b ^ T w ~~~~~~~~~~~~~ (9) \ end {ecuación} $$ display $$

Con restricciones dadas
1) l ≤ w ≤ u ;
2) Cw * d ;
donde w, l, u, d, b son vectores de valores reales n-dimensionales, Q es la matriz simétrica de la parte cuadrática, y el signo * significa cualquiera de las relaciones ≥ = ≤.
Como se puede ver en (8), la parte lineal b ^T w en nuestra función objetivo es igual a cero. Sin embargo, la matriz A no es simétrica, lo que, sin embargo, no impide llevarla a una forma simétrica sin cambiar la función misma. Para hacer esto, simplemente ponga en lugar de A la expresión$$ $ inline $ \ begin {ecation} \ frac {A ^ T + A} {2} \ end {ecation} $ inline $ Dado que la fórmula (9) incluye el coeficiente $$$\ frac {1} {2}$ entonces nosotros como Q podemos aceptar $$$A ^ T + A$ .

Las coordenadas de los vectores l y u especifican los límites del vector deseado y se encuentran en el rango [-1,1]. Como no asumimos ventas cortas de bonos, las coordenadas de los vectores en nuestro caso no son todas menores que 0. En el programa de ejemplo a continuación, por simplicidad, se supone que el vector l es cero, y los coeficientes del vector u son todos 0.3 . Sin embargo, nada nos impide mejorar el programa y hacer que los vectores de restricción sean más personalizables.

La matriz C en nuestro caso constará de dos líneas: 1) coeficientes de descuento, que, cuando se multiplican escalarmente por los pesos (el mismo ( w , k )), deben dar la tasa de rendimiento objetivo de la cartera; 2) una cadena que consiste en unidades. Es necesario establecer límites. $$$\ sum_ {i} w_i = 1$ .

Por lo tanto, la expresión Cw * d para nuestra tarea se verá así:

$$$$ display $$ \ begin {ecation} \ left \ {\ begin {array} {ccc} ({\ bf w, k}) = k_p \\ \ sum_ {i} w_i = 1 \\ \ end {array} \ right. ~~~~~~~~~~~~~ (10) \ end {ecuación} $$ display $$

Ahora pasamos a la implementación de software de la búsqueda de la cartera óptima. La base del optimizador cuadrático en ALGLIB es el objeto $$$\ tt \ small minqpstate$

alglib::minqpstate state; 

Para inicializar el optimizador, este objeto se pasa a la función minqpcreate junto con el parámetro de dimensión de tarea n

 alglib::minqpcreate(n, state); 

El siguiente punto más importante es la elección del algoritmo de optimización (solucionador). La biblioteca ALGLIB para la optimización cuadrática ofrece tres solucionadores:

• QP-BLEIC es el algoritmo más universal diseñado para resolver problemas con un número no muy grande (hasta 50 según las recomendaciones de la documentación) de restricciones lineales (de la forma Cw * d ). Al mismo tiempo, puede ser eficaz en tareas de gran dimensión (como se afirma en la documentación, hasta n = 10000).
• QuickQP es un algoritmo muy eficiente, especialmente cuando se optimiza una función convexa. Sin embargo, desafortunadamente, no puede funcionar con restricciones lineales, solo con condiciones de contorno (de la forma l≤w≤u ).
• Denso-AUL : optimizado para el caso de dimensiones muy grandes y una gran cantidad de restricciones. Pero, según la documentación, las tareas de pequeña dimensión y el número de restricciones se resolverán de manera más eficiente utilizando otros algoritmos.

Dadas las características anteriores, es obvio que el solucionador QP-BLEIC es el más adecuado para nuestra tarea.

Para indicarle al optimizador que use este algoritmo, debe llamar a la función $$$\ tt \ small minqpsetalgobleic$ . El objeto en sí y los criterios de detención se pasan a esta función, en la que no nos detendremos con más detalle: en el programa considerado aquí, se utilizan los valores predeterminados. La llamada a la función es la siguiente:

 alglib::minqpsetalgobleic(state, 0.0, 0.0, 0.0, 0); 

La inicialización adicional del solucionador incluye:

• La transferencia de la matriz de la parte cuadrática Q - $$$\ tt \ small alglib :: minqpsetquadraticterm (estado, qpma);$
• La transmisión del vector de la parte lineal (en nuestro caso, el vector cero) - $$$\ tt \ small alglib :: minqpsetlinearterm (estado, b);$
• La transferencia de los vectores de condición límite l y u - $$$\ tt \ small alglib :: minqpsetbc (estado, bndl, bndu);$
• Transmisión lineal $$$\ tt \ small alglib :: minqpsetlc (estado, c, ct);$
• Establecer la escala de coordenadas del espacio vectorial $$$\ tt \ small alglib :: minqpsetscale (estado, s);$

Hablemos de cada elemento:
Para especificar vectores y matrices, la biblioteca ALGLIB usa objetos de tipos especiales (enteros y de valor real): $$$\ tt \ small alglib :: integer \ _1d \ _array$ , $$$\ tt \ small alglib :: real \ _1d \ _array$ , $$$\ tt \ small alglib :: integer \ _2d \ _array$ , $$$\ tt \ small alglib :: real \ _2d \ _array$ . Para preparar la matriz, necesitamos un tipo $$$\ tt \ small real \ _2d \ _array$ . En el programa, primero cree una matriz A ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpma$ ), y luego de acuerdo con la fórmula $$$Q = A ^ T + A$ a partir de él construimos la matriz Q ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpmq$ ) Establecer dimensiones de matriz en ALGLIB es una función separada $$$\ tt \ small setlength (n, m)$ .

Para construir las matrices, necesitamos el vector de coeficientes de descuento ( k _i ) y la relación de duración con estos coeficientes ( $$$\ frac {D_j} {k_j}$ ):

 std::vector<float> disfactor; std::vector<float> durperytm; 

El fragmento de código que implementa la construcción de matrices se muestra en el siguiente listado:

 size_t n = durations.size(); alglib::real_2d_array qpma; qpma.setlength(n,n); // matrix nxn alglib::real_2d_array qpmq; qpmq.setlength(n,n); // matrix nxn for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpma(i,j) = durperytm[j]*disfactor[i]; //i,j   } for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpmq(i,j) = qpma(i,j) + qpma(j,i); } 

El vector de la parte lineal, como ya se indicó, es cero en nuestro caso, por lo que todo es simple:

 alglib::real_1d_array b; b.setlength(n); for (size_t i = 0; i < n; i++) b[i] = 0; 

Las condiciones de contorno del vector son transmitidas por una función. Para resolver este problema, se aplican condiciones límite muy simples: el peso de cada papel no debe ser inferior a cero (no permitimos posiciones negativas) y no debe exceder el 30%. Si lo desea, las restricciones pueden ser complicadas. Los experimentos con el programa mostraron que incluso un simple cambio en este rango puede afectar en gran medida los resultados. Por lo tanto, un aumento en el límite inferior y / o una disminución en el superior conduce a una mayor diversificación de la cartera final, ya que durante la optimización un solucionador puede excluir algunos valores del vector resultante (asignarles una ponderación del 0%) como no adecuados. Si establece el límite inferior de las escalas, digamos, en 5%, se garantiza que todos los documentos se incluirán en la cartera. Sin embargo, la duración calculada en tales configuraciones será, por supuesto, mayor que en el caso en que el optimizador puede excluir el papel.

Entonces, las condiciones de contorno son establecidas por dos vectores y transferidas al solucionador:

 alglib::real_1d_array bndl; bndl.setlength(n); for (size_t i = 0; i < n; i++) bndl[i] = 0.0; // low boundary alglib::real_1d_array bndu; bndu.setlength(n); for (size_t i = 0; i < n; i++) bndu[i] = 0.3;// high boundary alglib::minqpsetbc(state, bndl, bndu); 

Luego, el optimizador necesita pasar las restricciones lineales especificadas por el sistema (10). En ALGLIB, esto se hace usando la función $$$\ tt \ small alglib :: minqpsetlc (estado, c, ct)$ , donde c es la matriz que combina los lados izquierdo y derecho del sistema (10), es decir ver matriz $$$(C ~~ d)$ y ct es el vector de relaciones (es decir, correspondencias de la forma ≥, = o ≤). En nuestro caso, ct = (0,0), que corresponde a la relación '=' para ambas filas del sistema (10).

 for (size_t i = 0; i < n; i++) { c(0,i) = disfactor[i]; //   -    c(1,i) = 1; //   –  –    } c(0,n) = target_rate; //   ( ) –    c(1,n) = 1; //   ( ) –  ,   alglib::integer_1d_array ct = "[0,0]"; //   alglib::minqpsetlc(state, c, ct); 

La documentación de la biblioteca ALGLIB recomienda configurar la escala de variables antes de iniciar el optimizador. Esto es especialmente importante si las variables se miden en unidades, cuyo cambio difiere en órdenes de magnitud (por ejemplo, cuando se busca una solución, las toneladas se pueden cambiar en centésimas o milésimas, y los metros en unidades; el problema se puede resolver en el espacio de toneladas-metro), que afecta los criterios de abandono. Sin embargo, existe una reserva de que con la misma escala de variables, no es necesario establecer la escala. En el programa bajo consideración, todavía llevamos a cabo la tarea de escala en aras de un mayor rigor del enfoque, especialmente porque es muy simple de hacer.

 alglib::real_1d_array s; s.setlength(n); for (size_t i = 0; i < n; i++) s[i] = 1; //     alglib::minqpsetscale(state, s); 

A continuación, configuramos el optimizador como punto de partida. En general, este paso también es opcional, y el programa hace frente con éxito a la tarea sin un punto de partida claramente definido. Del mismo modo, por razones de rigor, establecemos el punto de partida. No seremos inteligentes: el punto de partida será el punto con los mismos pesos para todos los bonos.

 alglib::real_1d_array x0; x0.setlength(n); double sp = 1/n; for (size_t i = 0; i < n; i++) x0[i] = sp; alglib::minqpsetstartingpoint(state, x0); 

Queda por determinar la variable en la que el optimizador devolverá la solución encontrada y la variable de estado. Luego puede ejecutar la optimización y procesar el resultado

 alglib::real_1d_array x; //   alglib::minqpreport rep; //  alglib::minqpoptimize(state); //   alglib::minqpresults(state, x, rep); //      alglib::ae_int_t tt = rep.terminationtype; if (tt>=0) //       { std::cout << "   :" << '\n'; for(size_t i = 0; i < n; i++) //       { std::cout << (i+1) << ".\t" << bonds[i].bondname << ":\t\t\t " << (x(i)*100) << "\%" << std::endl; } for (size_t i = 0; i < n; i++) { for (size_t j = 0; j < n; j++) { qpmq(i,j) /= 2; } } } 

Especialmente, el tiempo de ejecución del programa no se midió en los experimentos, pero todo funciona muy rápido. Al mismo tiempo, está claro que es poco probable que un inversor privado optimice una cartera de más de 10-15 bonos.

También es importante tener en cuenta lo siguiente. El optimizador devuelve precisamente el vector de los pesos. Para obtener la duración calculada, debe usar directamente la fórmula (8). El programa puede hacer esto. Para este propósito, se agregaron especialmente dos funciones de multiplicar vectores y matrices. No los daremos aquí. Aquellos que lo deseen, los encontrarán fácilmente en los códigos fuente publicados.

Eso es todo Una inversión efectiva en instrumentos de deuda para todos.

PD: Comprender que elegir el código de otra persona no es la ocupación más atractiva, y para muchas personas que desean invertir, no es nada especializado, intentaré cambiar este programa un poco más tarde a un servicio web simple que todos puedan usar, independientemente del conocimiento de las matemáticas. y programación.