Integral de Euler-Poisson. Detalles sobre métodos de cálculo

En el artículo, en detalle, hasta el más mínimo detalle, se consideran tres métodos para tomar la integral de Euler-Poisson. En uno de los métodos, se deriva una fórmula de reducción auxiliar. Para encontrar algunas integrales complejas, uno puede usar fórmulas de reducción que le permitan a uno bajar el grado del integrando y calcular las integrales correspondientes en un número finito de pasos.

Esta integral se toma de la función gaussiana: $$$I = \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx}$
Hay una forma matemática muy interesante. Para encontrar la integral original, primero busque el cuadrado de esta integral y luego saque la raíz del resultado. Por qué Sí, porque es mucho más fácil e indoloro ir a las coordenadas polares. Por lo tanto, considere el cuadrado de la integral gaussiana:
$$$I ^ 2 = \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} \ int \ limits_0 ^ \ infty {e ^ {- y ^ 2} dy} = \ int \ limits_0 ^ \ infty { \ int \ limits_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ right)}}} dxdy$
Vemos que obtenemos una doble integral de alguna función $$$g \ left ({x, y} \ right) = \ exp \ left [{- \ left ({x ^ 2 + y ^ 2} \ right)} \ right]$ . Al final de esta integral de superficie se encuentra el elemento de área en el sistema de coordenadas cartesianas $$$dS = dxdy$ .
Ahora pasemos al sistema de coordenadas polares:

$$

$$\ begin {array} {l} dS = dxdy = rd \ varphi \ cdot dr \\ \ left. \ begin {array} {l} x = r \ cos \ varphi \\ y = r \ sin \ varphi \\ \ end {array} \ right | \ to x ^ 2 \ cos ^ 2 \ varphi + y ^ 2 \ sin ^ 2 \ varphi = r ^ 2 \ to x ^ 2 + y ^ 2 = r ^ 2 \\ \ end {array}$$

Aquí debe tenerse en cuenta que r puede variar de 0 a + ∞, porque x variado dentro del mismo rango. Pero el ángulo φ varía de 0 a π / 2, que describe la región de integración en el primer trimestre del sistema de coordenadas cartesianas. Sustituyendo en la fuente, obtenemos:

$$

$$\ begin {array} {l} I ^ 2 = \ int \ limits_0 ^ \ infty {\ int \ limits_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ right)}} } dxdy = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ int \ limits_0 ^ \ infty {e ^ {- r ^ 2}}} rd \ varphi dr = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} rdr} = \ int \ limits_0 ^ {\ frac {\ pi} {2}} { d \ varphi} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} \ frac {1} {2} d \ left ({r ^ 2} \ right)} = \\ = \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left ({\ left. {- e ^ {- r ^ 2}} \ right | _0 ^ \ infty} \ right) = \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left ({- e ^ {- \ infty} - \ left ({ - e ^ 0} \ right)} \ right) = \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} = \ frac {1} {2 } \ left ({\ left. \ varphi \ right | _0 ^ {\ frac {\ pi} {2}}} \ right) = \ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ to I = \ sqrt {\ frac {\ pi} {4}} = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}$$

Debido a la simetría de la integral y el rango positivo de valores del integrando, podemos concluir que

$$

$$\ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ cdot \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

¿Encontremos algunas soluciones más? Esto es interesante! :)

Considera la función $$$g \ left (t \ right) = \ left ({1 + t} \ right) e ^ {- t}$
Ahora recordemos las matemáticas escolares y realicemos un estudio simple de una función usando derivadas y límites. No es que consideremos límites complejos aquí (después de todo, no los pasan en la escuela), solo discutimos lo que sucederá con la función si su argumento tiende a cero o al infinito, por lo tanto, calcularemos el comportamiento asintótico, que siempre es muy importante en matemáticas. Esto es como una evaluación cualitativa de lo que está sucediendo.

$$

$$\ begin {array} {l} g \ left (t \ right) = \ left ({1 + t} \ right) e ^ {- t} \\ g '\ left (t \ right) = e ^ { - t} - \ left ({1 + t} \ right) e ^ {- t} = - te ^ {- t} \\ g '\ left (t \ right) = 0 \ to t = 0 \\ \ left [\ begin {array} {l} t <0 \ to - te ^ {- t}> 0 \ to g \ left (t \ right) - {\ rm {aumenta}} \\ t> 0 \ to - te ^ {- t} <0 \ to g \ left (t \ right) - {\ rm {disminuye}} \\ \ end {array} \ right. \\ g \ left (0 \ right) = \ left ({1 + 0} \ right) e ^ {- 0} = 1 \\ g \ left ({- 1} \ right) = \ left ({1 - 1} \ right) e ^ {- \ left ({- 1} \ right)} = 0 \\ g \ left (\ infty \ right) = \ left ({1 + \ infty} \ right) e ^ {- \ infty} = 0 \\ \ end {array}$$

Está limitado anteriormente por la unidad en el intervalo (-∞; + ∞) y cero en el intervalo [-1; + ∞).

Realizamos el siguiente cambio de variables $$$t = \ pm x ^ 2$
Y obtenemos:

$$

$$t = \ pm x ^ 2 \ to \ left \ {\ begin {array} {l} 0 <\ left ({1 - x ^ 2} \ right) e ^ {x ^ 2} <1 \\ 0 < \ left ({1 + x ^ 2} \ right) e ^ {- x ^ 2} <1 \\ \ end {array} \ right. \ to \ left \ {\ begin {array} {l} 0 <\ left ({1 - x ^ 2} \ right) <e ^ {- x ^ 2} \\ 0 <e ^ {- x ^ 2} <\ frac {1} {{1 + x ^ 2}} \\ \ end {array} \ right. $$$

En la primera desigualdad, restringimos la variación (0,1), y en la segunda, el intervalo (0; + ∞), elevamos ambas desigualdades a la potencia n, ya que las desigualdades con términos positivos pueden elevarse a cualquier grado positivo. Obtenemos:

$$

$$\ begin {array} {* {20} c} {\ left \ {\ begin {array} {l} \ left ({1 - x ^ 2} \ right) ^ n <e ^ {- nx ^ 2} \\ 0 <x <1 \\ \ end {array} \ right.} & {\ Left \ {\ begin {array} {l} e ^ {- nx ^ 2} <\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} \\ x> 1 \\ \ end {array} \ right.} \\ \ end {array}$$

Construyamos gráficas para n = 1 para demostrar las desigualdades.

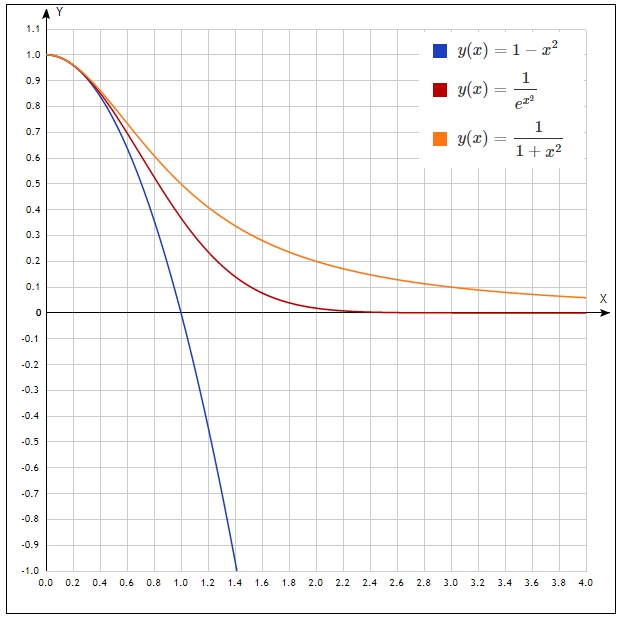
Ahora intentamos integrar las desigualdades dentro de los límites indicados en los sistemas correspondientes. E inmediatamente combine todo en una desigualdad:

$$

$$\ int \ limits_0 ^ 1 {\ left ({1 - x ^ 2} \ right) ^ n dx} <\ int \ limits_0 ^ 1 {e ^ {- nx ^ 2} dx} <\ int \ limits_0 ^ \ infty {e ^ {- nx ^ 2} dx} <\ int \ limits_0 ^ \ infty {\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} dx}$$

Nuevamente, si nos fijamos en los gráficos, entonces esta desigualdad es cierta.

Dado un pequeño reemplazo, es fácil ver que:

$$

$$\ int \ limits_0 ^ \ infty {e ^ {- nx ^ 2} dx} = \ left [\ begin {array} {l} p = \ sqrt nx \\ p ^ 2 = nx ^ 2 \\ \ frac { {dp}} {{\ sqrt n}} = dx \\ \ end {array} \ right] = \ frac {1} {{\ sqrt n}} \ int \ limits_0 ^ \ infty {e ^ {- p ^ 2} dp} = \ frac {1} {{\ sqrt n}} I$$

Es decir en esa gran desigualdad en el medio, tenemos la integral de Euler-Poisson, y ahora necesitamos encontrar las integrales que se encuentran en los límites de esta desigualdad.

Encuentra la integral desde el borde izquierdo:

$$

$$\ begin {array} {l} \ int \ limits_0 ^ 1 {\ left ({1 - x ^ 2} \ right) ^ n dx} = \ left [{\ begin {array} {* {20} c} \ begin {array} {l} x = \ sin t \\ dx = \ cos tdt \\ 1 - x ^ 2 = 1 - \ sin ^ 2 t = \ cos ^ 2 t \\ \ end {array} & \ begin {array} {l} x = 1 \ to t = \ arcsin 1 = \ frac {\ pi} {2} \\ x = 0 \ to t = \ arcsin 0 = 0 \\ \ end {array} \\ \ end {array}} \ right] = \\ = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n} t \ cdot \ cos tdt} = \ int \ limits_0 ^ { \ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} \\ \ end {array}$$

Para calcularlo y evaluarlo, primero encontremos una integral general. Ahora te mostraré cómo derivar la fórmula de reducción (en matemáticas, por tales fórmulas significan bajar el grado) para una integral dada.

$$

$$\ begin {array} {l} \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cos tdt} = \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cdot d \ left ({\ sin t} \ right)} = \\ = \ left [{\ begin {array} {* { 20} c} {u = \ cos ^ {n - 1} t} y {du = - \ left ({n - 1} \ right) \ cos ^ {n - 2} t \ sin tdt} \\ {dv = d \ left ({\ sin t} \ right)} & {v = \ sin t} \\ \ end {array}} \ right] = \\ = \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ sin ^ 2 tdt} = \\ = \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ left ({1 - \ cos ^ 2 t} \ right) dt} = \\ = \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ end {array}$$

$$

$$\ begin {array} {l} \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt } + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} \\ n \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt = \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt}} \\ \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt = \ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ frac {{n - 1}} {n} \ int \ limits_ \ alpha ^ \ beta {\ cos ^ { n - 2} tdt}} \\ \ end {array}$$

Ahora, si usamos la fórmula de reducción consideramos la misma integral, pero con nuestros límites de 0 a π / 2, entonces podemos hacer algunas simplificaciones:

$$

$$\ begin {array} {l} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ n tdt = \ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 1}} {n} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt}} = \ left [{\ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} = 0} \ right] = \\ = \ frac {{n - 1}} { n} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt} = \ frac {{n - 1}} {n} \ left ({\ frac {1 } {{n - 2}} \ left. {\ cos ^ {n - 3} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 3} } {{n - 2}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \\ = \ frac {{n - 1 }} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5 }} {{n - 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 6} tdt}} \ right)} \ right) = \\ = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5}} {{n - 4}} \ left ({\ frac {{n - 7}} {{n - 6}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 8} tdt}} \ right )} \ right)} \ right) = ... \\ \ end {array}$$

Como vemos, puedes bajarlo al infinito (depende de n). Sin embargo, hay una sutileza. La fórmula cambia dependiendo de si n es un número par o no.
Para esto, consideramos dos casos.

$$

$$\ begin {array} {l} n = 10: \\ \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {10} tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 2 tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ left ({\ frac {1 } {2} + \ frac {1} {2} \ cos 2t} \ right) dt} = \\ = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ left. {\ left ({\ frac {1} {2} t + \ frac {1} {2} \ sin 2t} \ right)} \ right | _0 ^ {\ frac {\ pi} {2}} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ cdot \ frac {\ pi} {4} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} {{10 \ cdot 8 \ cdot 6 \ cdot 4 \ cdot 2}} \ cdot \ frac {\ pi} {2} = \\ = \ frac {{\ left ({n - 1} \ right) !!}} {{n !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

$$

$$\ begin {array} {l} n = 9: \\ \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 9 tdt} = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} {{9 \ cdot 7 \ cdot 5 \ cdot 3}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos tdt} = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} {{9 \ cdot 7 \ cdot 5 \ cdot 3}} a la izquierda. {\ left ({\ sint} \ right)} \ right | _0 ^ {\ frac {\ pi} {2}} = \\ = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} { {9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} = \ frac {{\ left ({n - 1} \ right) !!}} {{n !!}} \\ \ end {array} $$$

Donde esta n !! - doble factorial. ¡El factorial doble de n se denota por n! y se define como el producto de todos los números naturales en el intervalo [1, n] que tiene la misma paridad que n

Debido al hecho de que 2n + 1 es un número impar para cualquier valor de n, obtenemos para el límite izquierdo de nuestra desigualdad:

$$

$$\ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} = \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}}$$

Encuentre la integral desde el borde derecho:
(Aquí usamos la misma fórmula de reducción que se demostró anteriormente)

$$

$$\ begin {array} {l} \ int \ limits_0 ^ \ infty {\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} dx = \ left [\ begin {array } {l} x = \ tan t \ to \ begin {array} {* {20} c} {x = 0 \ to t = 0} \\ {x = \ infty \ to t = \ frac {\ pi} {2}} \\ \ end {array} \\ dx = \ frac {{dt}} {{\ cos ^ 2 t}} \\ \ frac {1} {{1 + x ^ 2}}} \ \ frac {1} {{1 + \ tan ^ 2 t}} = \ cos ^ 2 t \\ \ end {array} \ right]} = \\ = \ int \ limits_0 ^ {\ frac {\ pi} {2} } {\ cos ^ {2n - 2} tdt} = \ left [{\ left ({2n - 2} \ right) - {\ rm {even}}} right] = \ frac {{\ left ({2n - 3} \ right) !!}} {{\ left ({2n - 2} \ right) !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

Después de haber estimado los lados izquierdo y derecho de la desigualdad, hacemos algunas transformaciones para evaluar los límites de los lados izquierdo y derecho de la desigualdad, siempre que n tienda a ∞:

$$

$$\ begin {array} {l} \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}} <\ frac {1} { {\ sqrt n}} \ cdot I <\ frac {{\ left ({2n - 3} \ right) !!}} {{\ left ({2n - 2} \ right) !!}} \ cdot \ frac {\ pi} {2} \\ \ sqrt n \ cdot \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}} <I <\ sqrt n \ cdot \ frac {{\ left ({2n - 3} \ right) !!}} {{\ left ({2n - 2} \ right) !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

Cuadrar ambos lados de la desigualdad:

$$

$$n \ cdot \ frac {{\ left ({\ left ({2n} \ right) !!} \ right) ^ 2}} {{\ left ({\ left ({2n + 1} \ right) !! } \ right) ^ 2}} <I ^ 2 <n \ cdot \ frac {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}} {{\ left ( {\ left ({2n - 2} \ right) !!} \ right) ^ 2}} \ cdot \ frac {{\ pi ^ 2}} {4}$$

Ahora hagamos una pequeña digresión. En 1655, John Wallis (un matemático inglés, uno de los precursores del análisis matemático) propuso una fórmula para determinar el número π. J. Wallis se acercó a ella, calculando el área de un círculo. Este producto converge extremadamente lento; por lo tanto, la fórmula de Wallis es de poca utilidad para el cálculo práctico del número π. Pero es genial para evaluar nuestra expresión :)

$$

$$\ pi = \ mathop {\ lim} \ limits_ {n \ to \ infty} \ frac {1} {n} \ left [{\ frac {{\ left ({2n} \ right) !!}} {{ \ left ({2n - 1} \ right) !!}}} \ right] ^ 2$$

Ahora transformamos nuestra desigualdad para que podamos ver dónde sustituir la fórmula de Wallis:

$$

$$\ begin {array} {l} \ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}} \ cdot \ frac {1} {n} \ cdot \ frac { {\ left ({\ left ({2n} \ right) !!} \ right) ^ 2}} {{\ left ({\ left ({2n - 1} \ right) !!} \ right) ^ 2} } <I ^ 2 <\ frac {1} {{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n - 2} \ right) !!} \ right) ^ 2 }} {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}}}} \ cdot \ frac {{\ pi ^ 2}} {4} \\ \ mathop {\ lim} \ limits_ {n \ to \ infty} \ left [{\ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}}} \ right] \ cdot \ mathop {\ lim} \ limits_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n} \ right) !!} \ right ) ^ 2}} {{\ left ({\ left ({2n - 1} \ right) !!} \ right) ^ 2}}} \ right] <I ^ 2 <\ frac {1} {{\ mathop {\ lim} \ limits_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n - 2} \ right) !!} \ derecha) ^ 2}} {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}}} \ right]}} \ cdot \ frac {{\ pi ^ 2} } {4} \\ \ frac {1} {4} \ cdot \ pi <I ^ 2 <\ frac {1} {\ pi} \ cdot \ frac {{\ pi ^ 2}} {4} \ to \ frac {\ pi} {4} <I ^ 2 <\ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ to I = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}$$

De la fórmula de Wallis se deduce que las expresiones izquierda y derecha tienden a π / 4 como n → ∞
Debido al hecho de que la función exp [-x²] es par, asumimos con seguridad que

$$

$$\ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ cdot \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

Por primera vez, Euler calculó la integral gaussiana unidimensional en 1729, luego Poisson encontró una manera simple de calcularla. En este sentido, se llamó la integral de Euler - Poisson.

Intentemos calcular la integral gaussiana. Se puede escribir en diferentes formas. Después de todo, nada cambia el nombre de la variable por la cual se está llevando a cabo la integración.

$$

$$\ begin {array} {l} I = \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} \\ I = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- y ^ 2} dy} = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- z ^ 2} dz} \\ \ end {array}$$

Puede pasar de coordenadas cartesianas tridimensionales a esféricas y considerar el cubo de la integral de Gauss.

$$

$$\ left \ {\ begin {array} {l} x = r \ sin \ theta \ cos \ varphi \\ y = r \ sin \ theta \ sin \ varphi \\ z = r \ cos \ theta \\ \ end {array} \ right. \ to x ^ 2 + y ^ 2 + z ^ 2 = r ^ 2$$

El jacobiano de esta transformación se puede calcular de la siguiente manera:

$$

$$\ begin {array} {l} J = \ left | {\ begin {array} {* {20} c} {\ frac {{\ partial x}} {{\ partial r}}} & {\ frac {{\ partial x}} {{\ partial \ theta}} } & {\ frac {{\ partial x}} {{\ partial \ varphi}}} \\ {\ frac {{\ partial y}} {{\ partial r}}} & {\ frac {{\ partial y }} {{\ partial \ theta}}} & {\ frac {{\ partial y}} {{\ partial \ varphi}}} \\ {\ frac {{\ partial z}} {{\ partial r}} } & {\ frac {{\ partial z}} {{\ partial \ theta}}} & {\ frac {{\ partial z}} {{\ partial \ varphi}}} \\ \ end {array}} \ derecho | = \ left | {\ begin {array} {* {20} c} {\ sin \ theta \ cos \ varphi} & {r \ cos \ theta \ cos \ varphi} & {- r \ sin \ theta \ sin \ varphi} \\ {\ sin \ theta \ sin \ varphi} y {r \ cos \ theta \ sin \ varphi} y {r \ sin \ theta \ cos \ varphi} \\ {r \ cos \ theta} y {- r \ sin \ theta} & 0 \\ \ end {array}} \ right | = \\ = r ^ 2 \ sin \ theta \\ \ end {array}$$

$$

$$\ begin {array} {l} I ^ 3 = \ int \ limits_ {- \ infty} ^ \ infty {\ int \ limits_ {- \ infty} ^ \ infty {\ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2 - y ^ 2 - z ^ 2}} dxdydz}} = \ int \ limits_0 ^ {2 \ pi} {\ int \ limits_0 ^ \ pi {\ int \ limits_0 ^ \ infty { e ^ {- r ^ 2} Jdrd \ theta d} \ varphi =}} \\ = \ int \ limits_0 ^ {2 \ pi} {d \ varphi} \ int \ limits_0 ^ \ pi {\ sin \ theta d \ theta} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} \\ \ end {array}$$

Calculamos las integrales secuencialmente, comenzando por la interna.

$$

$$\ begin {array} {l} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} = \ left [\ begin {array} {l} u = r \ to du = dr \\ dv = re ^ {- r ^ 2} dr \ to v = \ int {re ^ {- r ^ 2} dr} = \ frac {1} {2} \ int {e ^ {- r ^ 2} dr ^ 2} = - \ frac {1} {2} e ^ {- r ^ 2} \\ \ end {array} \ right] = \\ = \ left. {\ left ({- \ frac {1} {2} re ^ {- r ^ 2}} \ right)} \ right | _0 ^ \ infty + \ frac {1} {2} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ cdot \ frac {I} {2} = \ frac {I} {4} \\ \ int \ limits_0 ^ \ pi {\ sin \ theta d \ theta} = \ left. {\ left ({- \ cos \ theta} \ right)} \ right | _0 ^ \ pi = \ left ({- \ cos \ pi} \ right) - \ left ({- \ cos 0} \ right) = 1 + 1 = 2 \\ \ int \ limits_0 ^ {2 \ pi} {d \ varphi} = \ left. \ varphi \ right | _0 ^ {2 \ pi} = 2 \ pi \\ \ end {array}$$

Entonces como resultado obtenemos:

$$

$$\ begin {array} {l} I ^ 3 = 2 \ pi \ cdot 2 \ cdot \ frac {I} {4} \ to I ^ 3 = \ pi I \ to I ^ 2 = \ pi \ to I = \ sqrt \ pi \\ I = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ sqrt \ pi \\ \ end {array}$$

La integral de Euler-Poisson se usa a menudo en la teoría de la probabilidad.

Espero que para alguien el artículo sea útil y ayude a comprender algunas técnicas matemáticas :)