UPD: Como se solicitó en los comentarios, agrego un enlace al esquema giratorio de Javascript
Desafortunadamente, el código de JavaScript no se pudo insertar en el cuerpo de la publicación
Buenas tardes Recientemente leí un blog de un urbanista que estaba discutiendo cómo debería ser el esquema ideal del metro. El esquema del metro se puede dibujar en base a dos principios:
- El circuito debe ser conveniente y fácil de recordar y orientar.
- El esquema debe corresponder a la geografía de la ciudad.
Obviamente, estos principios son mutuamente excluyentes y el primer principio requiere una distorsión significativa de la realidad geográfica.
Es suficiente recordar cómo se ve el esquema del metro de Moscú con hermosos anillos y líneas rectas:
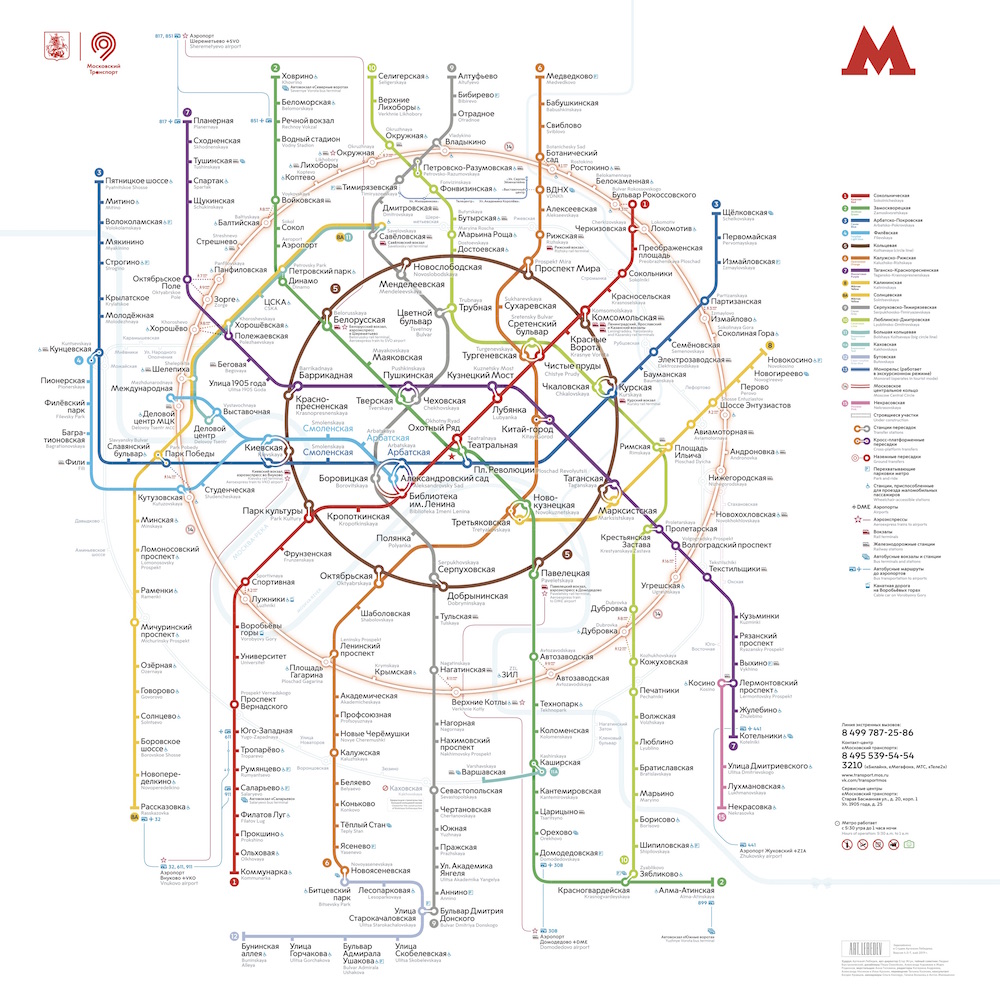
y comparar con un plan geográficamente preciso:

El plan muestra que los anillos no son perfectamente lisos y concéntricos, las líneas se doblan mucho más que en el esquema, y la densidad de las estaciones en el centro de la ciudad es tan alta que es casi imposible entender el plan.
Y aunque la segunda imagen refleja la realidad con mucha más precisión, está claro que es más conveniente utilizar el primer esquema para planificar una ruta en el metro.
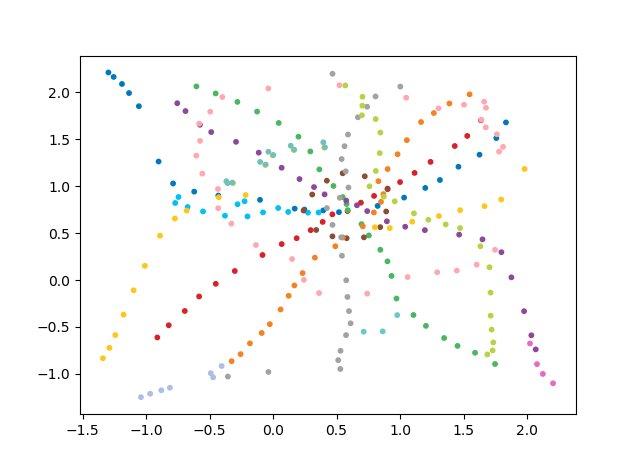
Y luego pensé lo siguiente: "¿Cómo sería el metro si el criterio para construir el circuito fuera el tiempo requerido para moverse de una estación a otra?" Es decir, si puede llegar de una estación a otra rápidamente, espacialmente se ubicarían cerca del diagrama.
Obviamente, en el espacio bidimensional es imposible dibujar un esquema en el que la distancia entre dos estaciones sea igual al tiempo de viaje de una a otra debido a la compleja topología del gráfico de metro.
También existe el presentimiento de que esto es exactamente posible cuando se construye un esquema en un espacio con una dimensión alta (la estimación superior es n-1, donde n es el número de estaciones). Para un espacio con un pequeño número de dimensiones, dicho esquema solo puede construirse aproximadamente.
La tarea de construir un mapa del metro por tiempo de viaje parece una tarea de optimización típica.
Supongamos que tenemos un conjunto inicial de coordenadas de todas las estaciones (X, Y, Z) y una matriz objetivo de tiempos por pares (distancias). Es posible construir la métrica de "incorrección" de un conjunto dado de coordenadas y luego minimizarla mediante el método de descenso de gradiente para cada una de las coordenadas de cada estación. Como métrica, podemos tomar una función simple de la desviación estándar de las distancias.
Bueno, lo único que queda es obtener datos sobre cuánto tiempo se debe dedicar a viajar desde cualquier estación del metro de Moscú a cualquier otra.
El primer pensamiento fue verificar la api del metro de Yandex y sacar esta información de allí. Lamentablemente, no se pudo encontrar la descripción de la API. Mire los tiempos manualmente en la aplicación durante mucho tiempo (en el metro hay 268 estaciones y el tamaño de la matriz de tiempo es 268 * 268 = 71824). Por lo tanto, decidí entender la fuente de datos de Yandex Metro. Como no hay acceso al servidor, se descargó un archivo apk con la aplicación y se encontraron los datos necesarios. Toda la información sobre el metro está notablemente estructurada y almacenada en formato JSON en la carpeta de archivos de la aplicación assets / metrokit / apk. Todos los datos se almacenan en estructuras autoexplicativas. Meta.json contiene información sobre las ciudades cuyos esquemas están presentes en la aplicación, así como la identificación de estos esquemas.
{ "id": "sc77792237", "name": { "en": "Nizhny Novgorod", "ru": " ", "tr": "Nizhny Novgorod", "uk": "і " }, "size": { "packed": 30300, "unpacked": 145408 }, "tags": [ "published" ], "aliases": [ "nizhny-novgorod" ], "logoUrl": "https://avatars.mds.yandex.net/get-bunker/135516/f2f0e33d8def90c56c189cfb57a8e6403b5a441c/orig", "version": "2c27fe1", "geoRegion": { "delta": { "lat": 0.168291, "lon": 0.219727 }, "center": { "lat": 56.326635, "lon": 43.992153 } }, "countryCode": "RU", "defaultAlias": "nizhny-novgorod" }
Por la identificación del esquema, encontramos la carpeta con JSON relacionada con Moscú.
El archivo data.json contiene información básica sobre el gráfico de metro, incluidos los nombres de los nodos del gráfico, ID de nodo, coordenadas geográficas de los nodos, información sobre las transiciones de una estación a otra (id, tiempo de transición, tipo de transición, ya sea conduciendo o caminando, en la calle o no, tiempo Estamos interesados en segundos) y también mucha información adicional sobre las entradas y salidas de la estación. Esto es bastante fácil de entender. Comencemos a escribir código para construir nuestro circuito.
Importamos las bibliotecas necesarias:
import numpy as np import json import codecs import networkx as nx import matplotlib.pyplot as plt import pandas as pd import itertools import keras import keras.backend as K from mpl_toolkits.mplot3d import Axes3D from mpl_toolkits.mplot3d.proj3d import proj_transform from matplotlib.text import Annotation import pickle
La estructura de los diccionarios y listas de Python es totalmente coherente con la estructura del formato json, por lo que leemos la información del metro y creamos objetos que corresponden a los objetos json.
names = json.loads(codecs.open( "l10n.json", "r", "utf_8_sig" ).read() ) graph = json.loads(codecs.open( "data.json", "r", "utf_8_sig" ).read() )
Creamos un diccionario que mapea los nodos del gráfico y la estación (esto es necesario porque las estaciones están asignadas a los nombres, no a los nodos del gráfico)
Además, por si acaso, guardaremos las coordenadas de los nodos para la posibilidad de construir un mapa geográfico (normalizado a un rango de 0-1)
nodeStdict={} for stop in graph['stops']['items']: nodeStdict[stop['nodeId']]=stop['stationId'] coordDict={} for node in graph['nodes']['items']: coordDict[node['id']]=(node['attributes']['geoPoint']['lon'],node['attributes']['geoPoint']['lat']) lats=[] longs=[] for value in coordDict.values(): lats.append(value[1]) longs.append(value[0]) for k,v in coordDict.items(): coordDict[k]=((v[0]-np.min(longs))/(np.max(longs)-np.min(longs)),(v[1]-np.min(lats))/(np.max(lats)-np.min(lats)))
Crea un gráfico de metro con conexiones. Establecemos el peso de cada conexión. El peso corresponde al tiempo de viaje. Eliminaremos nodos que no sean estaciones (en mi opinión, estas son salidas del metro y las conexiones a ellas son necesarias para las tarjetas Yandex al calcular el tiempo, pero no lo entendieron exactamente), crear un diccionario de identificación de nodo, el nombre real en ruso
G=nx.Graph() for node in graph['nodes']['items']: G.add_node(node['id'])
Definimos a qué rama (qué ID de rama) pertenece cada nodo (esto será necesario más adelante para colorear las líneas de metro en el diagrama)
def getlines(graph, G): nodetoline={} id_from={} id_to={} for lk in graph['tracks']['items']: id_from[lk['id']]=lk['fromNodeId'] id_to[lk['id']]=lk['toNodeId'] for line in graph['linesToTracks']['items']: if line['trackId'] in id_from.keys(): nodetoline[id_from[line['trackId']]]=line['lineId'] nodetoline[id_to[line['trackId']]]=line['lineId'] return nodetoline lines=getlines(graph,G)
La biblioteca networkx le permite encontrar la longitud de ruta más corta de un nodo a otro utilizando la función nx.shortest_path_length (G, id1, id2, weight = 'length'), por lo que podemos suponer que hemos terminado la preparación de datos. Lo siguiente que debe hacer es preparar un modelo que optimice las coordenadas de las estaciones.
Para hacer esto, descubriremos qué se le dará a la entrada, a la salida y cómo optimizaremos la matriz de coordenadas de la estación.
Supongamos que tenemos una matriz de todas las coordenadas (3x268). Multiplicar un vector de un solo calor (un vector donde 0 está en todas partes excepto una coordenada de unidad en lugar de n) de la dimensión 268 por esta matriz de coordenadas dará 3 coordenadas correspondientes a la estación n. Si tomamos un par de vectores de un solo calor y los multiplicamos por la matriz necesaria, obtenemos dos triples de coordenadas. A partir de un par de coordenadas, puede calcular la distancia euclidiana entre estaciones. Por lo tanto, podemos determinar la arquitectura de nuestro modelo:
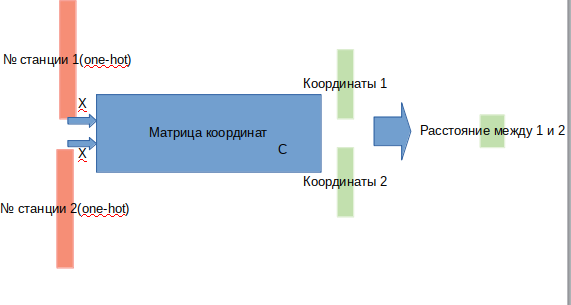
En la entrada damos un par de estaciones, en la salida obtenemos la distancia entre ellas.
Después de haber decidido el formato de datos para entrenar el modelo, prepararemos los datos utilizando la búsqueda de distancia en el gráfico:
myIDs=list(G.nodes()) listofinputs1=[] listofinputs2=[] listofoutputs=[] for pair in itertools.product(G.nodes(), repeat=2): vec1=np.zeros((len(myIDs))) vec2=np.zeros((len(myIDs))) vec1[myIDs.index(pair[0])]=1 vec2[myIDs.index(pair[1])]=1 listofinputs1.append(vec1) listofinputs2.append(vec2)
Optimizamos la matriz de coordenadas de la estación utilizando el método de descenso de gradiente.
Si usamos el marco de Keras para el aprendizaje automático, obtenemos lo siguiente:
np.random.seed(0) initweightmatrix=np.zeros((len(myIDs),3)) for i in range(len(myIDs)): initweightmatrix[i,:2]=coordDict[myIDs[i]] initweightmatrix[i,2]=np.random.randn()*0.001 def euclidean_distance(vects): x, y = vects sum_square = K.sum(K.square(x - y), axis=1, keepdims=True) return K.sqrt(K.maximum(sum_square, K.epsilon())) def eucl_dist_output_shape(shapes): shape1, shape2 = shapes return (shape1[0], 1) inp1=keras.layers.Input((len(myIDs),)) inp2=keras.layers.Input((len(myIDs),)) layer1=keras.layers.Dense(3,use_bias=None, activation=None) x1=layer1(inp1) x2=layer1(inp2) x=keras.layers.Lambda(euclidean_distance, output_shape=eucl_dist_output_shape)([x1, x2]) out=keras.layers.Dense(1,use_bias=None,activation=None)(x) model=keras.Model(inputs=[inp1,inp2],outputs=out) model.layers[2].set_weights([initweightmatrix]) model.layers[2].trainable=False model.compile(optimizer=keras.optimizers.Adam(lr=0.01), loss='mse')
tenga en cuenta que usamos coordenadas geográficas reales como coordenadas iniciales en la capa 1; esto es necesario para no caer en el mínimo local de la función de desviación estándar. Inicializamos la tercera coordenada en un valor distinto de cero para obtener un gradiente distinto de cero (si al principio el mapa es absolutamente plano, el desplazamiento de cualquier estación hacia arriba o hacia abajo será el mismo, por lo tanto, el gradiente es 0 y z no se optimizará). El último elemento de nuestro modelo (Denso (1)) afecta la escala del esquema para ajustarse a la línea de tiempo.
Mediremos la distancia en horas, no en segundos, ya que el orden de las distancias es de aproximadamente 1 hora, y para un entrenamiento más efectivo del modelo es importante que todos los valores (datos de entrada, pesos, objetivos) sean aproximadamente del mismo orden de magnitud. Si estos valores están cerca de 1, puede usar los valores de paso estándar para la optimización (0.001-0.01).
La línea model.layers [2] .trainable = False congela las coordenadas de las estaciones y en la primera etapa se varía un parámetro: la escala. Después de seleccionar la escala de nuestro esquema, descongelamos las coordenadas y las optimizamos ya:
hist=model.fit([listofinputs1,listofinputs2],listofoutputs,batch_size=71824,epochs=200) model.layers[2].trainable=True model.layers[-1].trainable=False model.compile(optimizer=keras.optimizers.Adam(lr=0.01), loss='mse') hist2=model.fit([listofinputs1,listofinputs2],listofoutputs,batch_size=71824,epochs=200)
vemos que alimentamos todos los pares de estaciones a la vez, a la salida todas las distancias y nuestra optimización es el descenso de gradiente de lote completo (un paso en todos los datos). La función de pérdida en este caso es la desviación estándar, y puede ver que era 0.015 al final del entrenamiento, lo que significa la desviación estándar de menos de 1 minuto para cualquier par de estaciones. En otras palabras, el esquema resultante le permite conocer con precisión la distancia que se requiere para llegar de una estación a otra por la distancia en línea recta entre estaciones con una precisión de + -1 minuto.
¡Pero veamos cómo se ve nuestro circuito!
obtenga las coordenadas de las estaciones, tome la codificación de color de las líneas y construya una imagen en 3D con firmas (el código para una hermosa muestra de firmas se toma
de aquí ):
class Annotation3D(Annotation): '''Annotate the point xyz with text s''' def __init__(self, s, xyz, *args, **kwargs): Annotation.__init__(self,s, xy=(0,0), *args, **kwargs) self._verts3d = xyz def draw(self, renderer): xs3d, ys3d, zs3d = self._verts3d xs, ys, zs = proj_transform(xs3d, ys3d, zs3d, renderer.M) self.xy=(xs,ys) Annotation.draw(self, renderer) def annotate3D(ax, s, *args, **kwargs): '''add anotation text s to to Axes3d ax''' tag = Annotation3D(s, *args, **kwargs) ax.add_artist(tag) fincoords=model.layers[2].get_weights() ccode={} for obj in graph['services']['items']: ccode[obj['id']]=('\#'+obj['attributes']['color'])[1:] xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] colors=[ccode[lines[idi]] for idi in myIDs] xyzn = zip(xn, yn, zn) fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(xn,yn,zn, c=colors, marker='o') for j, xyz_ in enumerate(xyzn): annotate3D(ax, s=labels[myIDs[j]], xyz=xyz_, fontsize=9, xytext=(-3,3), textcoords='offset points', ha='right',va='bottom') plt.show()
Como hubo dificultades para convertir a un formato 3D interactivo para el navegador, publico los gifs:
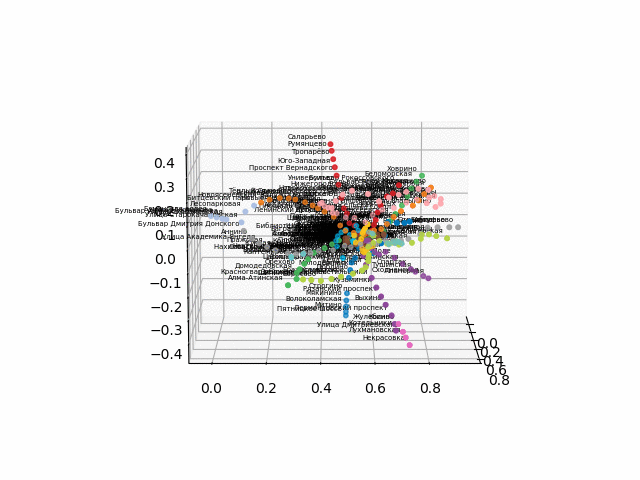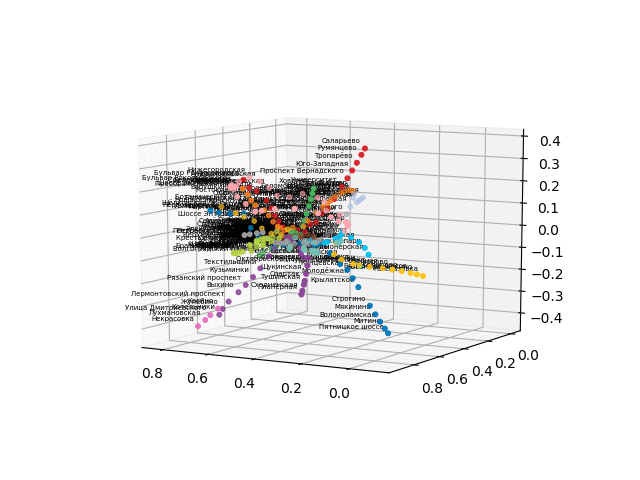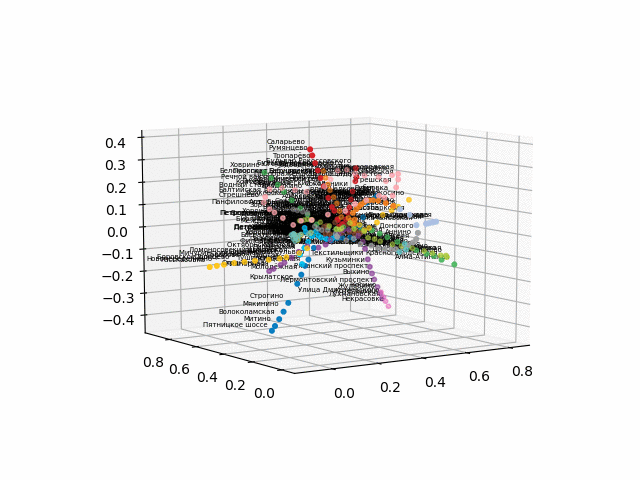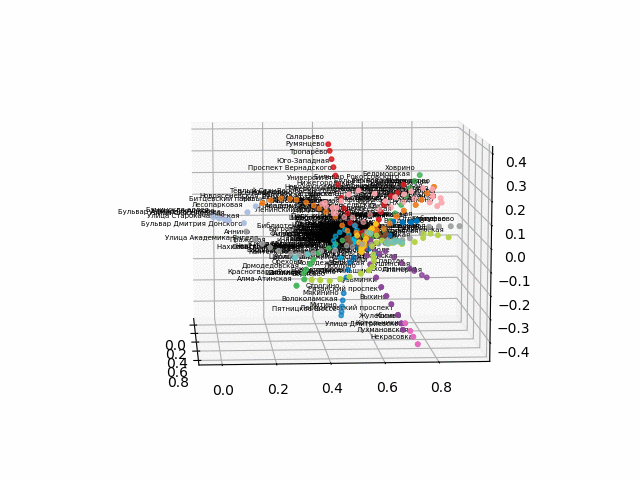
la versión sin texto se ve más bella y reconocible:
xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] colors=[ccode[lines[idi]] for idi in myIDs] xyzn = zip(xn, yn, zn) fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(xn,yn,zn, c=colors, marker='o') plt.show()
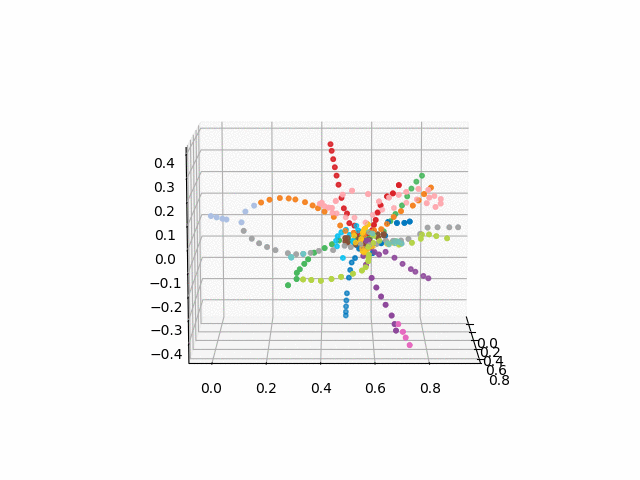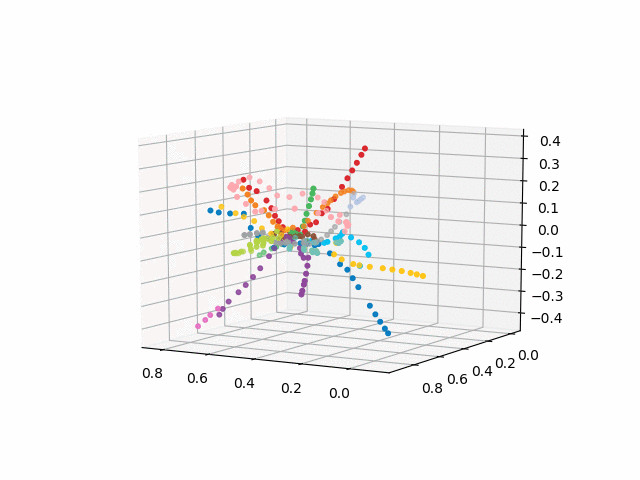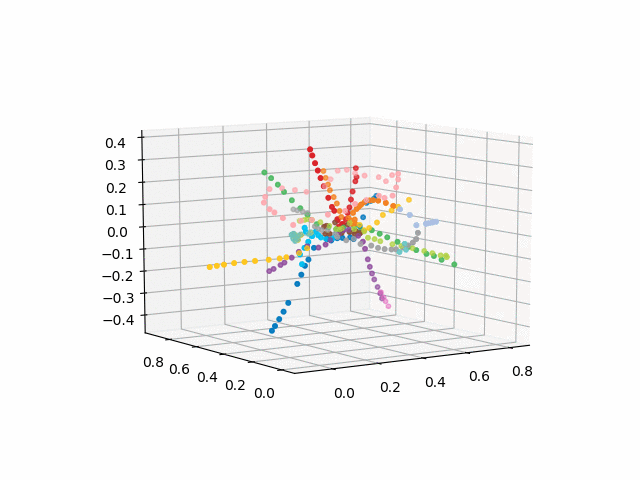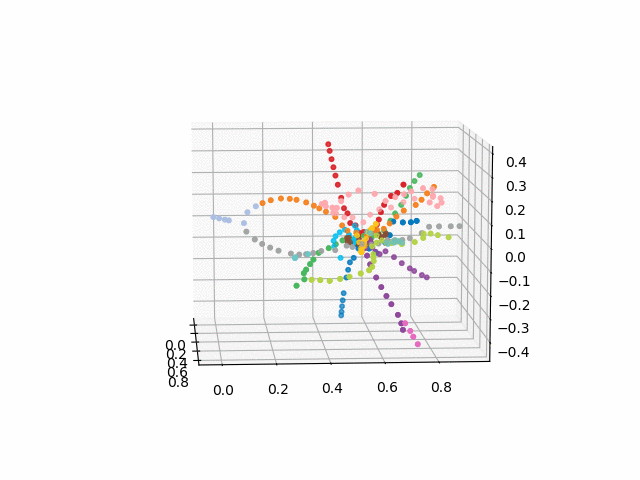
UPD: agrega líneas de metro del color deseado y crea un gif. Líneas negras - transiciones entre estaciones:
myedges=[(myIDs.index(edge[0]),myIDs.index(edge[1]))for edge in G.edges] xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] c=[ccode[lines[idi]] for idi in myIDs] fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(x,y,z, c=c, marker='o',s=25) for edge in myedges: col='black' if c[edge[0]]==c[edge[1]]: col=c[edge[0]] ax.plot3D([x[edge[0]], x[edge[1]]], [y[edge[0]], y[edge[1]]], [z[edge[0]], z[edge[1]]], col) ims = [] def rotate(angle): ax.view_init(azim=angle) rot_animation = animation.FuncAnimation(fig, rotate, frames=np.arange(0, 362, 3), interval=70) rot_animation.save('rotation2.gif', dpi=80, writer=matplotlib.animation.PillowWriter(80))
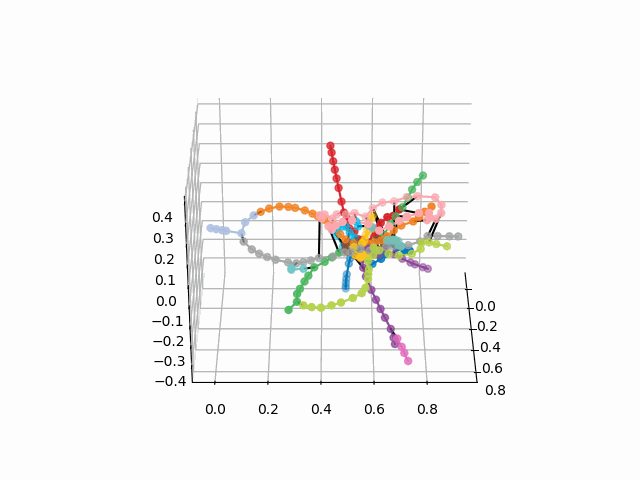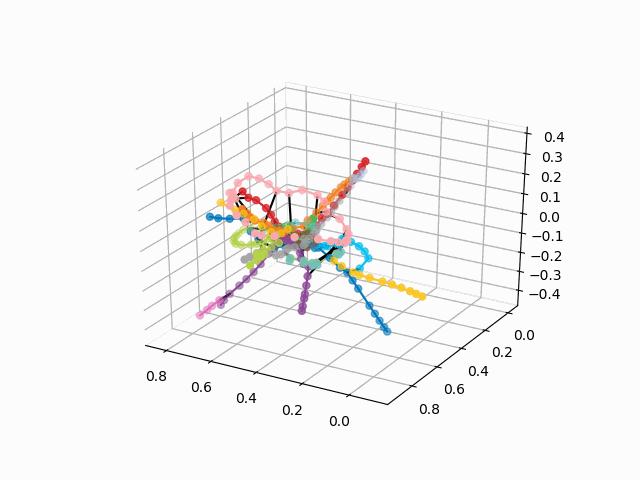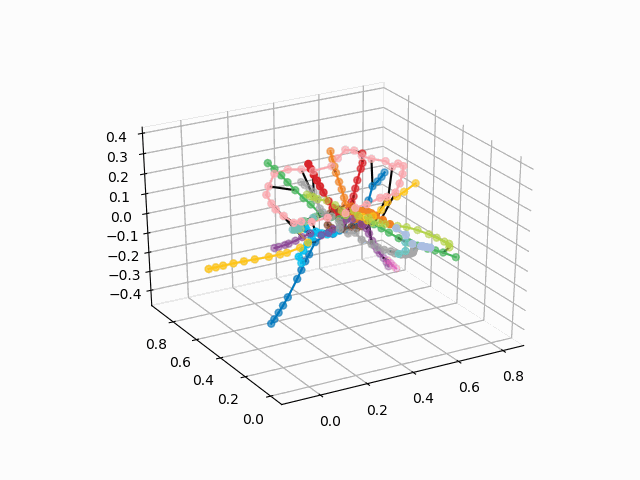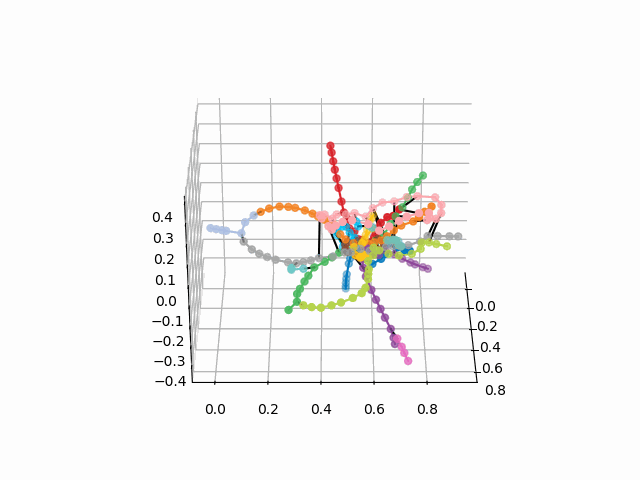
De este esquema, se pueden sacar algunas conclusiones interesantes que no son tan obvias de otros esquemas. Para algunas ramas, por ejemplo, verde, azul o morado, el MCC (anillo rosa) es casi inútil debido a los trasplantes incómodos, que se pueden ver en la distancia del anillo desde estas ramas. Las rutas más largas: desde un apartamento comunal hasta una carretera corta o viernes (caballos rojos y rosados / azules), las rutas largas también son la narración de Alma-Ata y el callejón Bunin-Nekrasovka. A juzgar por el plan, en el norte de Moscú hay una duplicación parcial de ramas grises y verdes claras: están cerca en el diagrama. Sería interesante ver cómo funcionan las nuevas líneas (WDC, BKL) y quién las usará con más frecuencia. En cualquier caso, espero que tales esquemas puedan ser herramientas interesantes para el análisis, la inspiración y la planificación de viajes.
PS 3D no es necesario, para la versión 2D es suficiente corregir ligeramente el código. Pero en el caso del esquema 2d, es imposible lograr tal precisión de distancias.