Una nueva solución a la paradoja de Fermi (por qué estamos solos en el universo)

Recientemente se me ocurrió una solución completamente nueva para la paradoja de Fermi . No volveré a contar lo que puedes leer en la wiki.



Voy a pasar al punto. Para resolver el problema, necesitamos algunos ingredientes.

1. MWI - la interpretación del multiverso.

Una cosa de ciencia popular bastante conocida y explicada (a menudo incorrectamente). Brevemente, en MWI el mundo está "enteramente" determinado, no hay accidente. Cuando los eventos tienen varios resultados, todos suceden, y luego, usando el mecanismo de decoherencia, aparecen diferentes "ramas" de la realidad en nuestro macro-mundo, donde fallan las diferentes copias de nuestra conciencia. Sin embargo, cada copia se considera la única, ya que no hay interacción entre las ramas.

2. Suicidio cuántico

La idea interesante y controvertida del suicidio cuántico se basa en MWI. Digamos, si el disparo del arma dependerá del evento cuántico, entonces poner un arma en la cabeza no pierde nada: en la rama donde disparó el arma, dejaremos de existir, y donde no disparamos, seguimos existiendo. Es decir, nuestra conciencia "cae" en la rama donde no se produjo el disparo.

El suicidio cuántico a menudo se critica por la siguiente razón: ¿qué pasa si la muerte por un disparo no es instantánea? Pero, ¿qué pasa si no morimos, sino que permanecemos paralizados? A continuación volveremos a este tema.

3. Catástrofe de vacío (descomposición del falso vacío)

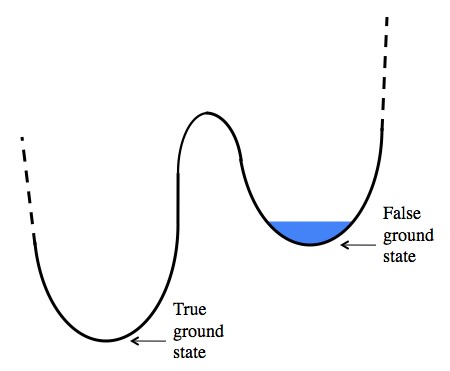
Es posible que nuestro vacío sea falso , es decir, nuestro vacío no es un estado inferior de vacío (en el sentido de la energía). Entonces es posible una transición espontánea en algún momento del vacío a un estado de energía más favorable. La diferencia en la energía del vacío se convierte en un desorden de una variedad de partículas (y posiblemente no existan en nuestro vacío), y su número es enorme. En realidad, el asunto que existía antes de tal evento puede ser descuidado.

Además, cuando surgió el centro de destrucción, es imposible detener el proceso, como el dominó, ¡el proceso se extiende en todas las direcciones y a la velocidad de la luz! Es decir, no tiene presagios, ni siquiera música perturbadora, como en las películas. Te sientas, bebes vino por la noche y miras las estrellas, y luego una vez, y no hay nada más que un plasma de partículas nuevas.

Nos gustaría creer que tal evento es muy muy muy poco probable, por ejemplo, Nick Bostrom me respondió con un enlace a su artículo con Tegmark, donde estimaron la probabilidad de tal evento "desde arriba":

arxiv.org/abs/astro-ph/0512204

Doom Factor.

¿Has notado que la catástrofe del vacío es mucho más adecuada para el suicidio cuántico que un arma? El proceso es instantáneo, no puede dejarte lisiado ... Es simplemente perfecto. Y entonces ... ¿Qué pasa si sucede regularmente, pero no nos damos cuenta? Me gustaría considerar un universo así.

Vamos a introducir el valor D (factor de muerte), que es proporcional a la probabilidad de descomposición espontánea del vacío. Para D = 1, uno de estos eventos ocurre una vez al año en un cubo 1x1x1 año luz. Los astrónomos ahora se encogen al usar el año luz como una medida de distancia, en lugar del parsec, pero en este caso realmente quiero medir el tiempo y la distancia en unidades "idénticas".

Universo condenado

Entonces, ¿cuál es la probabilidad de que sigamos vivos en un universo así? Necesitamos estimar el número de posibles desastres en el pasado, es decir, en nuestro cono de luz pasado. Este valor es igual a los cuatro volúmenes de un cono de 4 dimensiones de altura t, si las distancias se miden en años luz y el tiempo es simplemente en años (c = 1):

$$

Para nuestra historia, el tiempo en esta fórmula debe ser reemplazado por A = 13.8 mil millones de años, la edad del Universo. (de hecho, esto no es del todo honesto, ya que más cerca de la época del Big Bang, el cono está distorsionado debido a GR, pero ignoramos estos efectos aquí)

¡Oh suertudo!

Preguntando $$ obtenemos n = 379 millones. Es decir, la probabilidad de que no hayamos muerto es igual a $$ . Esto no debería sorprendernos, en el MWI las ramas se separan aún más, incluso en minutos y segundos.

Sin embargo, es interesante rastrear, y ¿cuándo (en promedio) fue el último evento de este tipo? Esto se puede hacer mediante la fórmula:

$$

El valor que obtenemos es bastante extraño (para la aleatoriedad D elegida por nosotros): aproximadamente 100 millones de años. Sin embargo, de hecho, esto no es sorprendente, ya que los 4 volúmenes del cono crecen muy rápidamente hasta la base. Es decir, el peligro que nos espera no proviene del vacío colapsado accidentalmente hace 4 años en Alpha Centauri, sino en el hecho de que estaremos cubiertos por una ola de descomposición que nos ha llegado desde las profundidades del Universo.

¿Qué tan rápido nos descomponemos?

Para la estimación, tomamos la derivada de n con respecto a t y obtenemos:

$$

Para nuestro valor de D, el valor de n aumenta en 0.11 cada año, es decir, más o menos, cada 9 años nuestras posibilidades se reducen a la mitad (pero, nuevamente, ¡no notamos esto para ningún valor de D!)

Argumento del día del juicio final

Nuevamente, no volveré a contar la wiki . Sin embargo, este argumento opera sobre las disposiciones (mal definidas) sobre 'almas' que 'infunden' (temporalmente) al azar en los cuerpos disponibles. Dado que los cuerpos son mucho más grandes al final de la civilización, la probabilidad de nacer en el Imperio Romano es muy pequeña.

Sin embargo, si el número de cuerpos se normaliza por la probabilidad de la existencia de ramas de la realidad (y debería normalizarse así, de lo contrario la regla de Bourne no funcionaría), entonces la distribución 'corregida' del número de cuerpos tiene un pico al principio del tiempo, y no hacia su final, es decir, invierte este argumento:



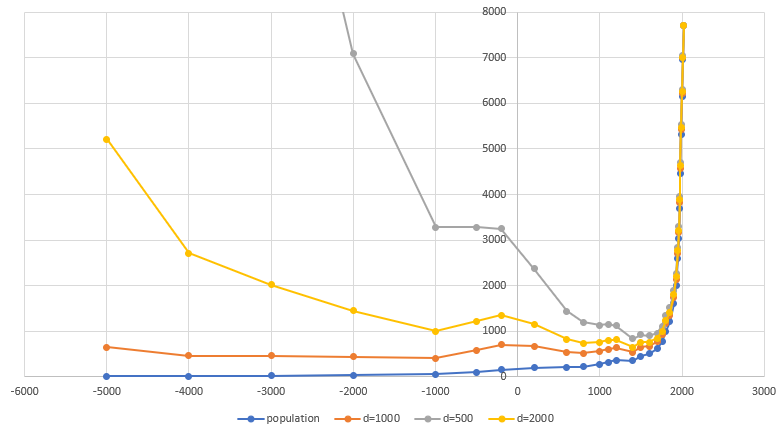
La línea azul en el gráfico muestra la población mundial en millones de personas en diferentes momentos. Otras curvas 'normalizan' estos valores teniendo en cuenta que la amplitud de probabilidad en el pasado fue mayor (para valores más pequeños de D, por ejemplo, d = 1000 - la probabilidad disminuye a la mitad en 1000 años, y no en 9 años)

Paradoja de Fermi

Finalmente, llegamos a la paradoja misma. Aplicamos el argumento del día del juicio final invertido a las civilizaciones (además, cuando el tiempo de desarrollo de diferentes civilizaciones diverge en millones de años, el efecto comienza a aparecer a partir de valores D mucho más bajos). Es decir, la probabilidad de nacer en una civilización tardía es insignificante.

Es decir, ¡nacimos en la primera, y hasta ahora la única civilización!

Encuesta

El artículo wiki proporciona varias soluciones al problema. Vota por los que creas que son probables. Tomé las opciones de la versión en inglés de Wiki (hay algunas en la versión rusa), pero combiné algunas