Al primer conocimiento de los métodos cuasi-newtonianos, uno puede sorprenderse dos veces. En primer lugar, después de un rápido vistazo a las fórmulas, surgen dudas de que esto pueda funcionar en absoluto. Sin embargo, funcionan. Además, parece dudoso que funcionen bien. Y es aún más sorprendente ver cuán más rápidos son que las diversas variaciones del descenso de gradiente, no en tareas especialmente construidas, sino en tareas reales tomadas de la práctica. Y si después de esto todavía hay dudas mezcladas con interés, entonces debes entender por qué esto funciona en absoluto.
Ya se han considerado el origen y las ideas básicas que impulsan los métodos de gradiente, incluido el método de Newton. Es decir, confiamos en la información sobre el comportamiento de la función en la vecindad de la posición actual, lo que nos da un análisis matemático simple. Como mínimo, se asumió que la información sobre los primeros derivados estaba disponible para nosotros. ¿Qué pasa si esto es todo lo que está disponible para nosotros? ¿El gradiente descendente es nuestra oración? Por supuesto, sí, a menos que de repente recuerde que estamos tratando con un
proceso en el que la función objetivo se procesa correctamente. Y si es así, ¿por qué no usamos la información acumulada sobre el comportamiento de la función para hacer que nuestra caminata en su superficie sea un poco menos ciega?
La idea de utilizar información sobre el camino cubierto es el núcleo de la mayoría de las formas de acelerar los métodos de descenso. Este artículo analiza una de las formas más efectivas, aunque no la más barata, de dar cuenta de este tipo de información, lo que lleva a la idea de métodos cuasi-newtonianos.
Para comprender de dónde crecen las patas de los métodos cuasi-newtonianos y de dónde proviene el nombre, nuevamente tenemos que volver al método de minimización basado en la solución directa de la ecuación de punto estacionario
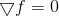
. Así como la consideración del método de Newton aplicado a la solución de esta ecuación nos llevó al método de optimización del mismo nombre (que, a diferencia de su progenitor, tiene una región de convergencia global), podemos esperar que la consideración de otros métodos para resolver sistemas de ecuaciones no lineales sea fructífera. planificar ideas para construir otros métodos de optimización.
Metodos
Permíteme recordarte que el método de Newton para resolver el sistema de ecuaciones
, se basa en el reemplazo en el vecindario de algún punto cercano a la solución
las funciones
su aproximación lineal
donde
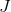
Es un operador lineal que, cuando
es un vector y
tiene derivadas parciales con respecto a cada variable, coincide con la matriz de Jacobi
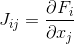
. A continuación, se resuelve la ecuación.
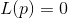
y punto
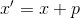
tomado como una nueva aproximación a la solución deseada. Es simple y funciona.
Pero, ¿y si por alguna razón no podemos calcular la matriz de Jacobi? Lo primero que viene a la mente en este caso es que si no podemos calcular las derivadas parciales analíticamente, entonces podemos obtener una aproximación numérica para ellas. La opción más simple (aunque de ninguna manera la única) para tal aproximación puede ser la fórmula de diferencias finitas correctas:
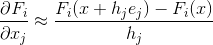
donde
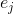
Es el j-ésimo vector base. La matriz compuesta de tales aproximaciones se denotará por
. Un análisis de cuánto reemplazo
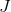
en
en el método de Newton, su convergencia afecta, se dedica un número bastante grande de trabajos, pero en este caso estamos interesados en otro aspecto. Es decir, tal aproximación requiere el cálculo de la función en N puntos adicionales y, además, la función
en estos puntos
interpola la función
es decir
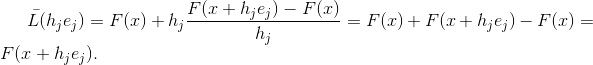
No todas las aproximaciones de la matriz de Jacobi tienen esta propiedad, pero cada matriz de una función afín que tiene esta propiedad es una aproximación de la matriz de Jacobi. De hecho, si
y
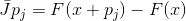
luego en
. Esta propiedad, es decir, la propiedad de interpolación, nos brinda una forma constructiva de generalizar el método de Newton.
Dejar
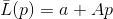
- función que cumple el requisito
para algún sistema de vectores linealmente independientes
. Entonces dicha función se llama función
secante , y la ecuación que lo define es
la ecuación secante . Si el sistema de vectores
está completo (es decir, hay exactamente N de ellos y todavía son linealmente independientes) y, además, el sistema de vectores
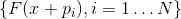
linealmente independiente entonces
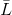
definido de forma única.
Cualquier método basado en el cambio local de ecuación.
ecuación de la forma
donde
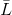
satisface
la ecuación secante , llamada
método secante .
Una pregunta justa surge sobre cómo construir la secante para una función de la manera más racional.
. La siguiente línea de razonamiento parece obvia: dejar que se construya un modelo afín en el punto x que interpola la función dada en los puntos
. Solución de ecuaciones
nos da un nuevo punto
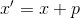
. Luego para construir un modelo afín en un punto
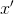
es más razonable elegir puntos de interpolación para que el valor
ya conocido, es decir, sacarlos del set
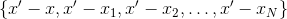
. Existen diferentes opciones para los puntos a elegir entre los muchos utilizados anteriormente. Por ejemplo, puede tomar como puntos de interpolación aquellos en los que
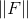
importa menos o solo el primero
puntos. En cualquier caso, parece obvio que
debe incluirse en muchos puntos de interpolación para el nuevo modelo afín. Así que más allá
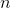
Los pasos del proceso iterativo en nuestro conjunto pueden ser hasta
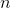
desplazamientos construidos en puntos previamente pasados. Si el proceso se construye de tal manera que el nuevo modelo afín no use más
de los valores anteriores, entonces dicho proceso se llama método secante de punto p.
A primera vista, podría parecer que el método secante de punto N es el mejor candidato para el papel de reemplazar el método de Newton, ya que hace el máximo uso de la información que obtenemos en el proceso de resolución, mientras minimizamos el número de cálculos adicionales: utilizamos el valor de la función N puntos pasados. Lamentablemente, esto no es así. El caso es que el sistema vectorial
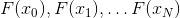
obstinadamente se niega a ser linealmente independiente con un N. suficientemente grande. Además, incluso si esta condición se cumple y el modelo afín correspondiente todavía existe, existe la posibilidad de que las direcciones
También demuestra ser linealmente independiente, resulta aún menos. Y esto implica el hecho de que el modelo afín, aunque existe, es degenerado y prácticamente inadecuado.
En general, el más estable es el método secante de 2 puntos. Es decir, un método en el que en cada iteración tenemos que calcular valores N-1 adicionales de la función. Esto claramente no es adecuado para nuestros propósitos prácticos.
Entonces la pregunta es: ¿qué fue todo esto?
Métodos cuasi-newtonianos para resolver ecuaciones.
La salida es simple, aunque no obvia. Si no tenemos la capacidad técnica, basada en los valores ya calculados, para determinar de manera única un modelo afín que satisfaga la ecuación secante, entonces no es necesario. Tomamos la ecuación de secantes como base, pero exigiremos que se satisfaga solo para algún sistema incompleto de vectores
. En otras palabras, requeriremos que la condición de interpolación se satisfaga solo para un número suficientemente pequeño de valores conocidos. Por supuesto, en este caso ya no podemos garantizar que la matriz utilizada en dicho modelo tenderá a la matriz de Jacobi, pero no la necesitaremos. Además de esto, el modelo afín debe interpolar la función en el punto actual, es decir.
, obtenemos la siguiente formulación del método secante:
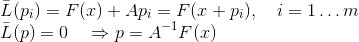
Bruiden fue el primero en considerar métodos de este tipo para m = 1, llamándolos cuasi-newtonianos. Está claro que la condición secante en este caso nos permite identificar de manera única la matriz
solo si se le imponen condiciones adicionales, y cada una de esas condiciones adicionales da lugar a un método separado. Bruyden mismo razonó de la siguiente manera:
como el movimiento en la dirección desde el punto 
hasta el punto 
no nos proporciona ninguna información adicional sobre cómo cambia la función de otra manera que direcciones, luego el efecto de la nueva función afín en el vector 
debería diferir del efecto de la función anterior en el mismo vector cuanto menos, más diferente de . Como último recurso, cuando ortogonal , el comportamiento de la nueva función no debe ser diferente del comportamiento de la anterior.
La idea de Breiden es brillante en su simplicidad. De hecho, si no tenemos nueva información sobre el comportamiento de la función, lo mejor que podemos hacer es tratar de no dañar la anterior. Entonces la condición adicional
para todos
tal que
le permite determinar de manera única la matriz de la nueva transformación: se obtiene al agregar una corrección de rango 1 a la matriz anterior.
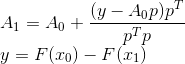
Sin embargo, a pesar de la simplicidad y consistencia de las conclusiones hechas por Bruiden, no proporcionan el punto de apoyo que podría servir como base para construir otros métodos similares. Afortunadamente, hay una expresión más formal de su idea. A saber, la matriz construida de esta manera
Resulta ser la solución al siguiente problema:
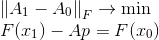
La restricción de la tarea no es más que la ecuación secante, y la condición de minimización refleja nuestro deseo de guardar tanta información como sea posible en la matriz.
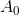
. La medida de la discrepancia entre las matrices en este caso es la norma de Frobenius, en la cual el problema planteado tiene una solución inequívoca. Esta formulación bien puede servir como punto de partida para construir otros métodos. Es decir, podemos cambiar tanto la
medida por la cual evaluamos los cambios introducidos como las
condiciones impuestas en la matriz. En general, ya se puede trabajar con tal formulación del método.
Métodos de optimización cuasi-Newton
Habiendo entendido la idea principal, finalmente podemos volver a los problemas de optimización y notar que aplicar la fórmula de Bruyden para recalcular el modelo afín no se ajusta muy bien a nuestra tarea. De hecho, la primera derivada de la función de gradiente
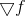
no hay nada más que la matriz de Hesse, que por construcción es simétrica. Al mismo tiempo, la actualización de acuerdo con la regla de Bruyden conduce a una matriz asimétrica.
incluso si
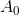
fue simétrico Esto no significa que el método de Bruden no se pueda aplicar para resolver la ecuación del punto estacionario, pero con base en dicha regla de actualización, es poco probable que podamos construir buenos métodos de optimización. En general, es bastante obvio que el método cuasi-newtoniano debería funcionar mejor y con mayor precisión el sistema de condiciones del problema describe los detalles de una matriz de Jacobi específica.
Para corregir este inconveniente, agregamos una restricción adicional al problema de minimización de Bruden, que requiere explícitamente que la nueva matriz sea simétrica junto con la anterior:
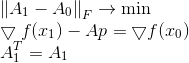
La solución a este problema es
Aqui
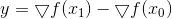
, y la fórmula de recálculo matricial lleva el nombre de sus creadores: Powell, Shanno y Bruyden (PSB). La matriz resultante es simétrica, pero claramente no positiva definida, aunque solo de repente
no será colineal
. Y
vimos que la certeza positiva es altamente deseable en los métodos de optimización.
Nuevamente, corregiremos la condición del problema, usando esta vez la norma de Frobenius escalada como una medida de la divergencia de la matriz.
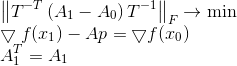
El origen de tal enunciado de la pregunta es un gran tema separado, pero es interesante que si la matriz T es tal que
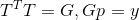
(es decir, G también es una matriz de transformación afín que satisface la ecuación secante para la dirección p), entonces la solución a este problema resulta ser independiente de la elección de T y conduce a la fórmula de actualización
conocida como la fórmula de Davidon-Fletcher-Powell. Este método de actualización se ha probado en la práctica, ya que tiene la siguiente propiedad:
si 
y 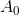positivo definitivo entonces También positivamente identificado.Observo después que si la primera condición no se cumple, entonces no existe una función afín con una matriz definida positiva que satisfaga la ecuación secante.
Si en el problema que conduce al método DFP, tomamos, como una medida de la discrepancia de modelos afines, la distancia no entre las matrices mismas, sino entre las matrices inversas a ellas, obtenemos un problema de la forma
Su solución es una fórmula bien conocida, descubierta casi simultáneamente por Breiden, Fletcher, Goldfarb y Shanno (BFGS).
Hasta la fecha, se cree que el recálculo de acuerdo con esta fórmula es el más eficiente desde el punto de vista computacional y, al mismo tiempo, es menos propenso a la degeneración de la matriz con un gran número de iteraciones. En las mismas condiciones que DFP, esta fórmula conserva la propiedad de la definición positiva.
Todos los métodos descritos para actualizar la matriz requieren una corrección de rango 2. Esto hace que invertir la matriz sea fácil y sencillo
usando la fórmula de Sherman-Morrison y el valor
.
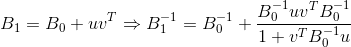
siempre que el denominador de la fórmula sea distinto de cero. No daré fórmulas específicas para actualizar las matrices inversas de los métodos enumerados, ya que son fáciles de encontrar o derivar de forma independiente. Lo único que debe tenerse en cuenta en este caso es que las variantes de los métodos con la actualización de la matriz inversa suelen ser mucho menos estables (es decir, sufren más errores de redondeo) que las que sugieren actualizar la matriz original. Es más eficiente actualizar no la matriz en sí, sino su descomposición de Cholesky (a menos, por supuesto, que se produzca dicha descomposición), ya que dicha opción de implementación es más estable numéricamente y, además, minimiza el costo de resolver una ecuación que determina la dirección del movimiento.
Queda por considerar la cuestión de cómo debería verse la primera matriz en el proceso cuasi-newtoniano. Aquí todo es obvio: cuanto más cerca esté de la matriz de Hesse o de su versión corregida, si el Hesse de repente no resulta ser definitivo positivo, mejor será desde el punto de vista de la convergencia. Sin embargo, en principio, cualquier matriz definida positiva puede ser adecuada para nosotros. La versión más simple de dicha matriz es única, y luego la primera iteración coincide con la iteración del descenso del gradiente. Fletcher y Powell demostraron (naturalmente, para el método DFP) que si la función cuadrática se minimiza, independientemente de qué matriz (positiva definida) se use como la iteración inicial de DFP, conducirán a una solución en exactamente N iteraciones, donde N es dimensión del problema, y la matriz cuasi-newtoniana coincide con la matriz de Hesse en el punto mínimo. En el caso general no lineal de dicha felicidad, por supuesto, no esperaremos, pero esto al menos da razones para no preocuparnos demasiado por la mala elección de la matriz inicial.
Conclusión
El enfoque descrito para la construcción de métodos cuasi-newtonianos no es el único posible. Como mínimo, los descubridores de los métodos cuasi-newtonianos descritos y muchos investigadores posteriores llegaron a las mismas fórmulas sobre la base de consideraciones completamente diferentes. Sin embargo, es interesante que tan pronto como apareció un cierto método cuasi-newtoniano, independientemente del método para obtenerlo, después de un tiempo bastante corto quedó claro que era una solución a un problema de optimización muy fácil de interpretar. En mi opinión, es notable que sea posible traer algún denominador común para métodos tan diversos, ya que esto proporciona la base para construir otros métodos que tengan mejor en cuenta los detalles de una tarea en particular. En particular, existen métodos cuasi-newtonianos diseñados para actualizar matrices dispersas, métodos en los que la menor cantidad posible de elementos están sujetos a cambios, y muchos otros serían una fantasía.
También se debe tener en cuenta que los métodos de métricas variables, a pesar de su nombre, no siempre conducen a la construcción de matrices, que en realidad son métricas, aunque lo hacen cada vez que es posible.
Por lo general, este no es un gran problema, pero aquellos que desean protegerse de una posible vergüenza pueden recurrir a los mismos trucos que se hicieron para superar un problema similar con el método de Newton, por ejemplo, cambiando la dirección o aplicando el esquema de Levenberg-Marquardt . Es cierto, en este caso, las preguntas sobre cómo elegir la forma de una región de confianza volverán a ser relevantes, pero aquí tienes que elegir el menor de los males. Otra solución al problema es utilizar métodos de búsqueda lineal para garantizar que se cumplan las condiciones necesarias para mantener una certeza positiva. La regla de Wolfe garantiza el cumplimiento de esta condición, mientras que las reglas de Armijo y Goldstein no lo hacen.Teóricamente, es casi imposible determinar cuál de la gran cantidad de métodos cuasi-newtonianos posibles será el más efectivo con respecto a una determinada clase de problemas. Por lo general, al formular un método, se limitan a mostrar su efectividad para minimizar una función cuadrática (por cierto, un método se considera efectivo si conduce a una solución exacta en N iteraciones, es decir, no más lentamente que los métodos directos para resolver SLAEs). En casos más raros, uno puede encontrar estudios del orden de convergencia del método (que generalmente es superlineal, es decir, significativamente mejor que el que nos brinda el descenso de gradiente), estabilidad y otras características de interés. Pero en general, el único criterio razonable para juzgar la efectividad de un método particular para una clase particular de tareas es la práctica.Así que palas en mano, y éxito en la aplicación.