El tema de Allocators a menudo aparece en Internet: de hecho, un Allocator es una especie de piedra angular, el corazón de cualquier aplicación. En esta serie de publicaciones quiero hablar en detalle sobre un asignador muy entretenido y eminente:
JeMalloc , respaldado y desarrollado por Facebook y utilizado, por ejemplo, en
bionic [Android] lib C.En la red, no pude encontrar ningún detalle que revelara completamente el alma de este asignador, lo que finalmente afectó la imposibilidad de sacar conclusiones sobre la aplicabilidad de JeMalloc para resolver un problema en particular. Salió mucho material y, para leerlo, no fue agotador, propongo comenzar con lo básico: Estructuras de datos básicas utilizadas en JeMalloc.
Debajo del gato, estoy hablando de
Pairing Heap y
Bitmap Tree , que forman la base de JeMalloc. En esta etapa, no toco el tema del
subprocesamiento múltiple y el bloqueo de grano fino , sin embargo, al continuar la serie de publicaciones, definitivamente te contaré sobre estas cosas, por lo cual, de hecho, se crean varios tipos de Exóticos, en particular el que se describe a continuación.
Bitmap_s es una estructura de datos en forma de árbol que le permite:
- Encuentre rápidamente el primer bit de activación / desactivación en una secuencia de bits determinada.
- Cambie y obtenga el valor de un bit con el índice i en una secuencia de bits dada.
- El árbol se construye de acuerdo con una secuencia de n bits y tiene las siguientes propiedades:
- La unidad base del árbol es el nodo, y la unidad base del nodo es el bit. Cada nodo consta de exactamente k bits. El bitness de un nodo se selecciona de modo que las operaciones lógicas en un rango seleccionado de bits se calculen de la manera más rápida y eficiente posible en una computadora determinada. En JeMalloc, un nodo está representado por un tipo largo sin signo .
- La altura del árbol se mide en niveles y para una secuencia de n bits es H = niveles.
- Cada nivel del árbol está representado por una secuencia de nodos, que es equivalente a una secuencia de poco
- El nivel más alto (raíz) del árbol consta de k bits y el más bajo de n bits.
- Cada bit de un nodo de nivel L determina el estado de todos los bits de un nodo secundario de nivel L - 1: si un bit se establece como ocupado, entonces todos los bits de un nodo secundario también se configuran como ocupado, de lo contrario, los bits de un nodo secundario pueden tener estado 'ocupado' y 'libre'.
Es razonable representar bitmap_t en dos matrices: la primera, de una dimensión igual al número de todos los nodos de árbol, para almacenar los nodos de árbol, y la segunda, de la dimensión de altura de árbol, para almacenar el desplazamiento del comienzo de cada nivel en la matriz de nodos de árbol. Con este método de especificar un árbol, el elemento raíz puede ir primero, y luego, en secuencia, los nodos de cada uno de los niveles. Sin embargo, los autores de JeMalloc almacenan el elemento raíz en último lugar en la matriz, y frente a él están los nodos de los niveles de árbol subyacentes.
Como ejemplo ilustrativo, tome una secuencia de 92 bits y K = 32 mente. Suponemos que el estado es 'libre', denotado por un solo bit, y el estado 'ocupado', cero. Suponga también que en la secuencia de bits original, el bit con índice 1 (contando desde cero, de derecha a izquierda en la figura) está configurado como ocupado. Entonces bitmap_t para tal secuencia de bits se verá como la imagen a continuación:
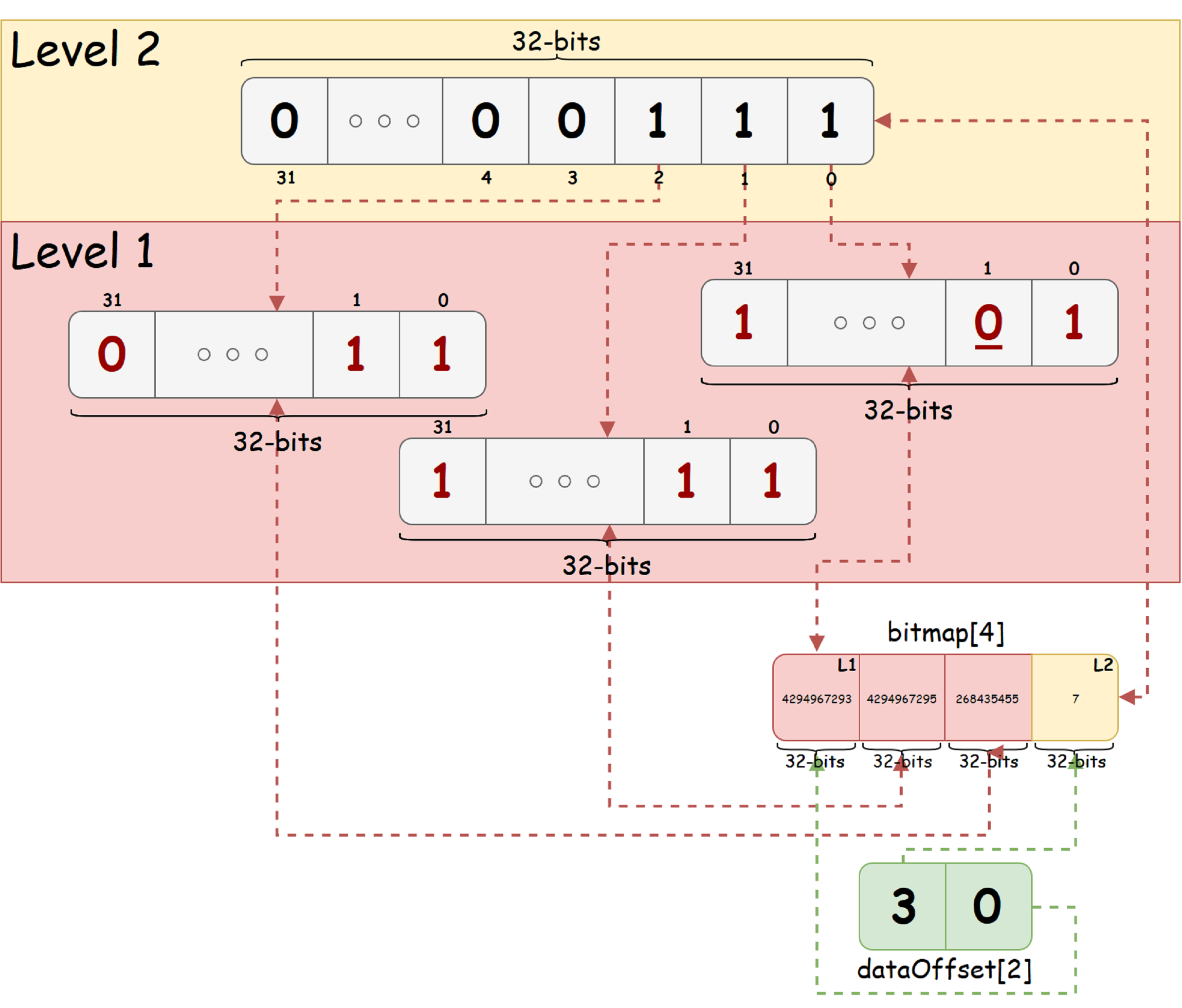De la figura vemos que el árbol resultante tiene solo dos niveles. El nivel raíz contiene 3 bits unitarios, lo que indica la presencia de bits libres y ocupados en cada uno de los nodos secundarios del bit correspondiente. En la esquina inferior derecha, puede ver la vista de árbol en dos matrices: todos los nodos de árbol y las compensaciones de cada nivel en la matriz de nodos.Suponiendo que bitmap_t está representado por dos matrices (una matriz de datos y una matriz de compensaciones a nivel de árbol en la matriz de datos), describimos la operación de búsqueda del primer bit menos significativo en un bitmap_t dado:
- Comenzando desde el nodo raíz, realizamos la operación de búsqueda para el primer bit menos significativo del nodo: para resolver este problema, los procesadores modernos proporcionan instrucciones especiales que pueden reducir significativamente el tiempo de búsqueda. Guardaremos el resultado encontrado en la variable FirstSetedBit .
- En cada iteración del algoritmo, mantendremos la suma de las posiciones de los bits encontrados: countOfSettedBits + = FirstSetedBit
- Usando el resultado del paso anterior, vamos al nodo hijo del primer bit de unidad menos significativo del nodo y repetimos el paso anterior. La transición se lleva a cabo de acuerdo con la siguiente fórmula simple:
- El proceso continúa hasta que se alcanza el nivel más bajo del árbol. countOfSettedBits : el número del bit deseado en la secuencia de bits de entrada.
Pairing Heap es una estructura de datos de árbol similar a un montón que le permite:
- Inserte un elemento con una complejidad de tiempo constante de O (1) y un costo amortizado de O (log N) u O (1) , según la implementación.
- Buscar al menos por tiempo constante - O (1)
- Combine dos pares de emparejamiento con una complejidad de tiempo constante: O (1) y costo amortizado O (log N) u O (1) , según la implementación
- Eliminar un elemento arbitrario (en particular, uno mínimo) con una estimación de complejidad temporal en O (N) y una estimación de complejidad amortizada en O (log N)
Más formalmente hablando, Pairing Heap es un árbol arbitrario con una raíz dedicada que satisface las propiedades del montón (la clave de cada vértice no es menor / no más que la clave de su padre).
Un almacenamiento dinámico de emparejamiento típico en el que el valor del nodo secundario es menor que el valor del nodo primario (también conocido como almacenamiento dinámico de emparejamiento mínimo) se parece a esto:
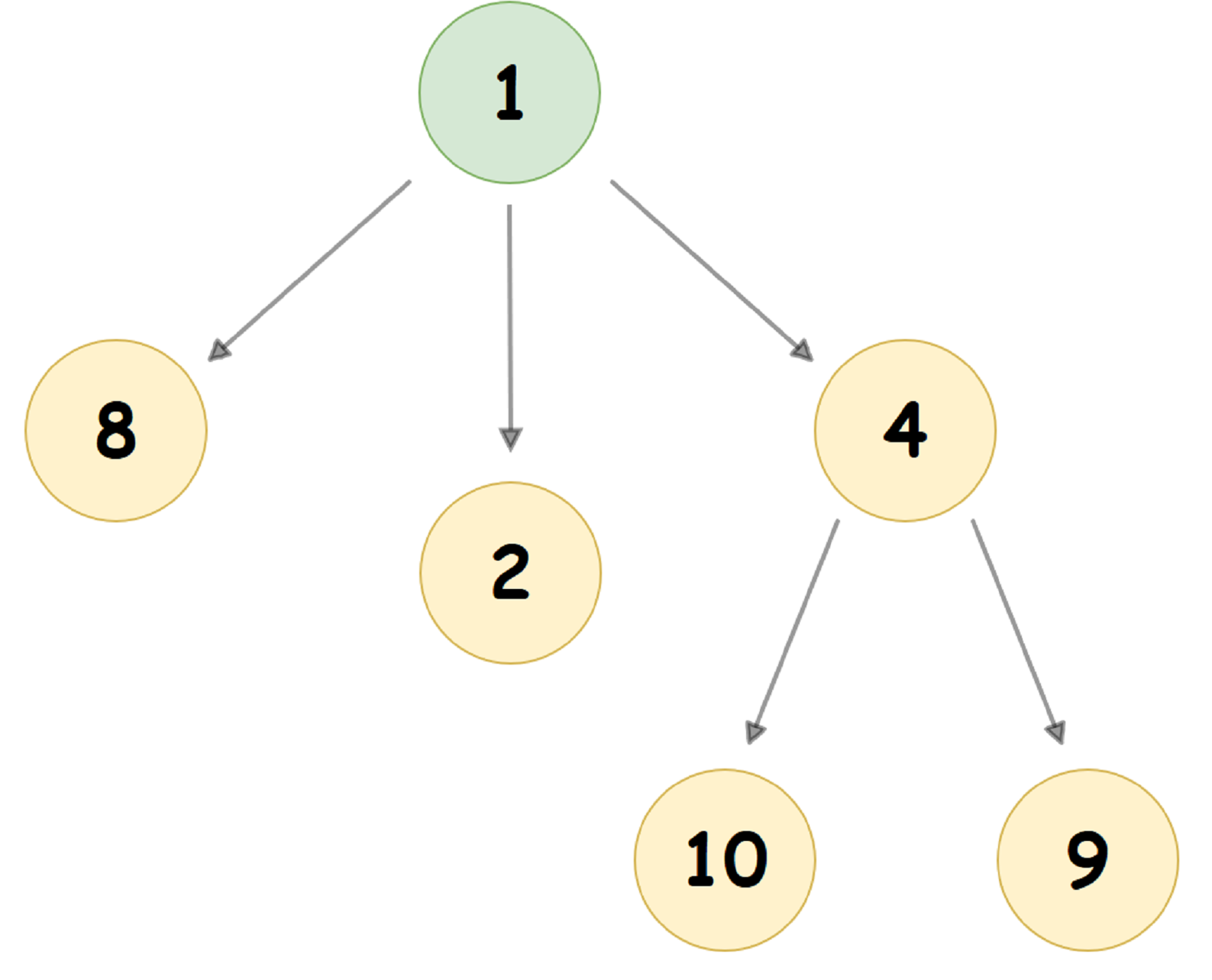
En la memoria de la computadora, Pairing-Heap, como regla, se presenta de una manera completamente diferente: cada nodo del Árbol almacena 3 punteros:
- Puntero al nodo hijo más a la izquierda del nodo actual
- Puntero al hermano izquierdo del nodo
- Puntero al hermano derecho del nodo
Si falta alguno de los nodos indicados, el puntero de nodo correspondiente se anula.
Para el montón presentado en la figura anterior, obtenemos la siguiente representación:
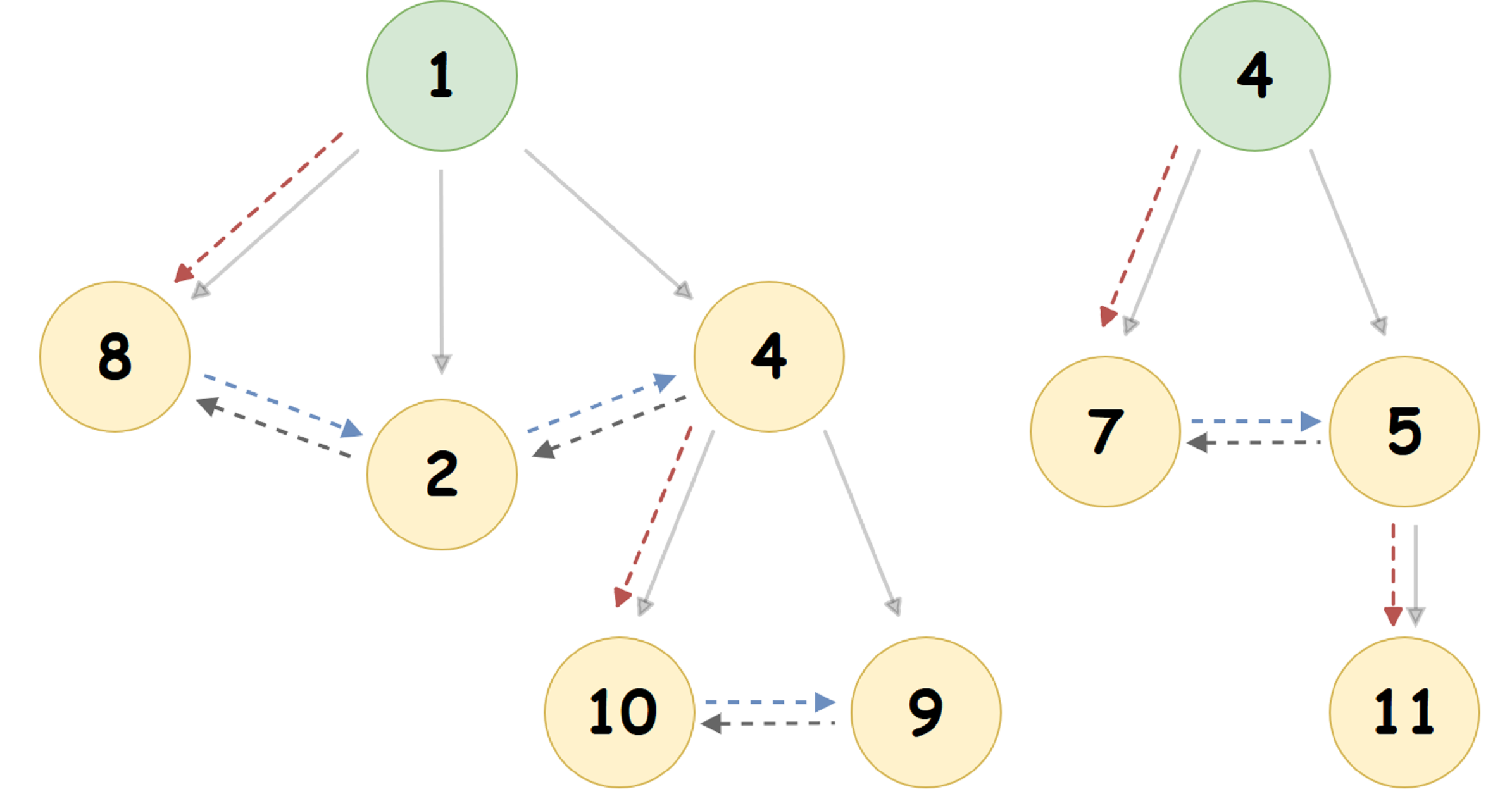Aquí, el puntero al nodo secundario más a la izquierda se indica mediante una flecha punteada roja, el puntero al hermano derecho del nodo es azul y el puntero al hermano izquierdo es gris. La flecha sólida muestra la representación de Heap de emparejamiento en forma de árbol que es común para una persona.Tenga en cuenta los siguientes dos hechos:
- En la raíz del montón no siempre hay hermanos derechos e izquierdos.
- Si cualquier nodo U tiene un puntero distinto de cero al nodo secundario más a la izquierda, entonces este nodo será la 'Cabeza' de la lista doblemente vinculada de todos los nodos secundarios de U. Esta lista se llama siblingList.
A continuación, enumeramos el algoritmo de las operaciones principales en
Min Pairing-Heap :
- Insertar nodo en el montón de emparejamiento:
Deje que se le dé un montón de emparejamiento con una raíz y un valor en él {R, V_1} , así como un nodo {U, V_2} . Luego, al insertar un nodo U en un montón de emparejamiento dado:
- Si se cumple la condición V_2 <V_1: U se convierte en el nuevo nodo raíz del montón, 'desplazando' la raíz R a la posición de su nodo hijo izquierdo. Al mismo tiempo, el hermano derecho del nodo R se convierte en su nodo más a la izquierda más antiguo, y el puntero al nodo más a la izquierda del nodo R se convierte en cero.
- De lo contrario: U se convierte en el nodo hijo más a la izquierda de la raíz de R, y su hermano mayor es el nodo más a la izquierda de la raíz de R.
- Combinando dos pares de emparejamiento:
Deje que se den dos Montones de emparejamiento con raíces y valores en ellos {R_1, V_1} , {R_2, V_2}, respectivamente. Describimos uno de los algoritmos para fusionar tales montones en el montón de emparejamiento resultante:
- Elija el montón con el valor más bajo en la raíz. Deja que sea un montón de {R_1, V_1}.
- 'Separe' la raíz R_1 del montón seleccionado: para esto, simplemente anulamos su puntero al nodo secundario más a la izquierda.
- Con el nuevo puntero al nodo secundario más a la izquierda de la raíz R_1, cree la raíz R_2. Tenga en cuenta que de ahora en adelante, R_2 pierde el estado raíz y es un nodo normal en el montón resultante.
- Establecemos el hermano derecho del nodo R_2: con el nuevo valor hacemos que el puntero anterior (antes de poner a cero) al nodo hijo más a la izquierda de la raíz R_1, y para R_1, respectivamente, actualice el puntero al hermano izquierdo.
Considere el algoritmo de fusión utilizando un ejemplo específico:
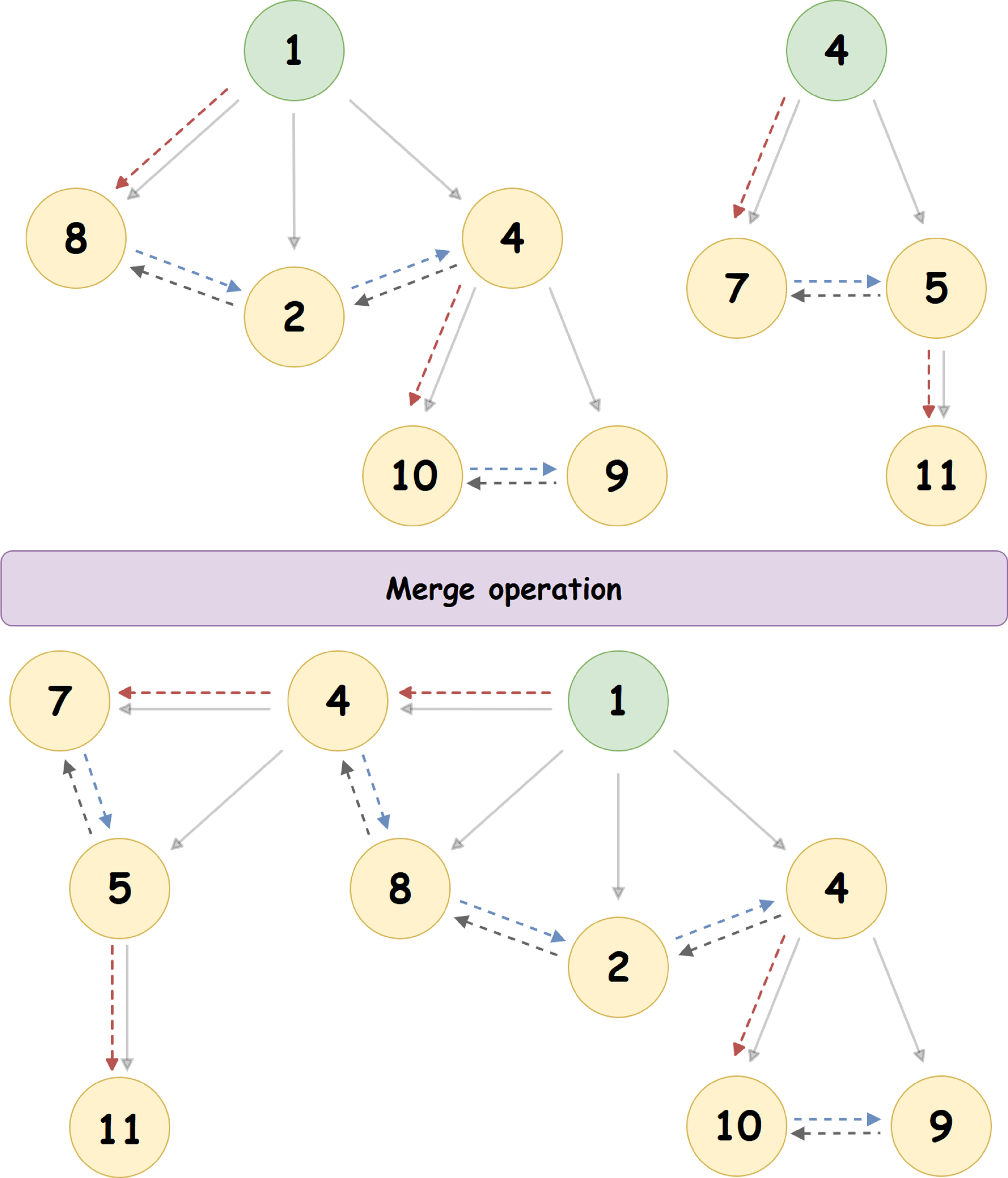Aquí, el montón con la raíz '4' se une al montón con la raíz '1' (1 <4), convirtiéndose en su nodo hijo más a la izquierda. El puntero al hermano derecho del nodo '4' - se actualiza, así como el puntero al hermano izquierdo del nodo '8'.- Eliminar la raíz (nodo con el valor mínimo) Heap de emparejamiento:
Existen varios algoritmos para eliminar un nodo de un Heap de emparejamiento, que garantizan una estimación amortizada de la complejidad en O (log N). Describimos uno de ellos, llamado algoritmo multipass y utilizado en JeMalloc:
- Eliminamos la raíz del montón dado, dejando solo su nodo secundario más a la izquierda.
- El nodo secundario más a la izquierda forma una lista doblemente vinculada de todos los nodos secundarios del nodo primario y, en nuestro caso, la raíz eliminada previamente. Revisaremos secuencialmente esta lista hasta el final y, considerando los nodos como las raíces del montón de emparejamiento independiente, realizaremos la operación de fusionar el elemento actual de la lista con el siguiente, colocando el resultado en una cola FIFO preparada previamente.
- Ahora que la cola FIFO está inicializada, iteraremos sobre ella, realizando la operación de fusionar el elemento actual de la cola con el siguiente. El resultado de la fusión se coloca al final de la cola.
- Repetimos el paso anterior hasta que un elemento permanezca en la cola: el montón de emparejamiento resultante.
Un buen ejemplo del proceso descrito anteriormente:
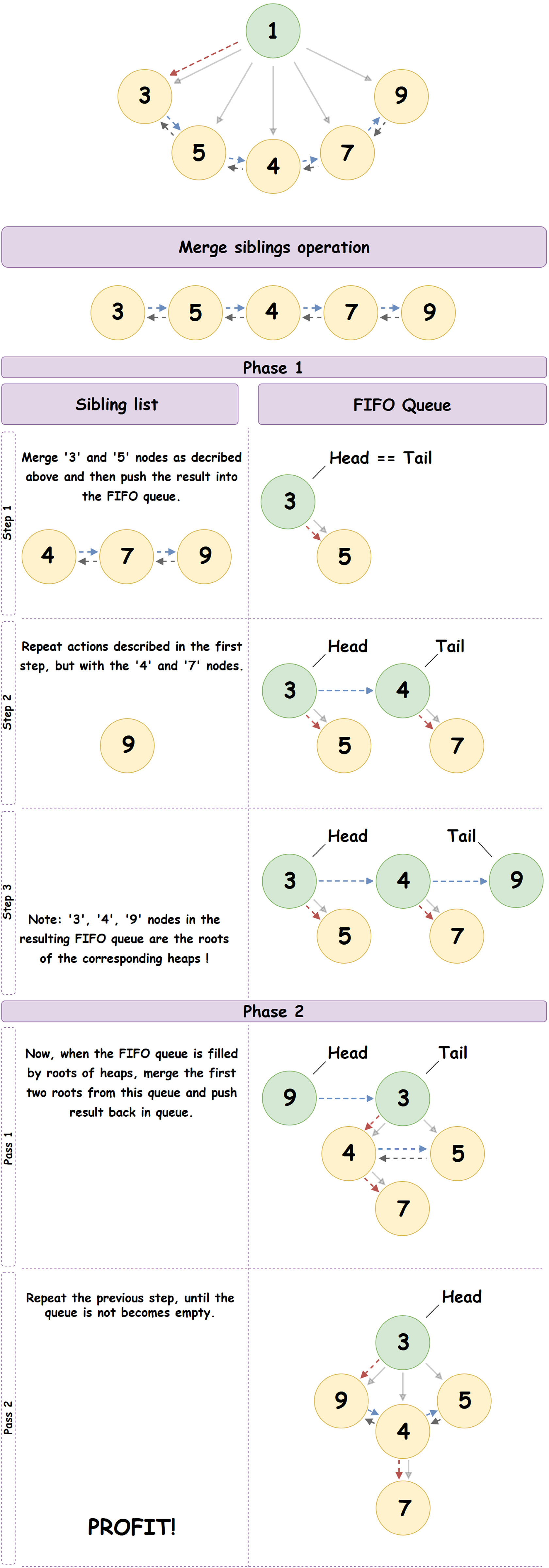
- Eliminación de un montón de emparejamiento de nodo no raíz arbitrario:
Considere el nodo eliminado como la raíz de algún subárbol del montón original. Primero, elimine la raíz de este subárbol, siguiendo el algoritmo descrito anteriormente para eliminar la raíz del montón de emparejamiento, y luego, realice el procedimiento de fusión del árbol resultante con el original. - Obtención del elemento mínimo de almacenamiento dinámico de emparejamiento:
Simplemente devuelva el valor de la raíz del montón.
Sin embargo, nuestro conocimiento de Pairing Heap no termina ahí: Pairing Heap le permite realizar algunas operaciones no de manera inmediata, sino solo cuando sea necesario. En otras palabras, Pairing Heap le permite realizar operaciones
'perezosamente' , reduciendo así el costo amortizado de algunas de ellas.
Supongamos que hicimos K inserciones y K elimina en Pairing Heap. Obviamente, el resultado de estas operaciones se vuelve necesario solo cuando solicitamos el elemento mínimo del montón.
Consideremos cómo cambiará el algoritmo de acciones de las operaciones descritas anteriormente durante su implementación diferida:
Aprovechando el hecho de que la raíz de Kuchi tiene al menos dos punteros nulos, usaremos uno de ellos para representar el encabezado de una lista doblemente vinculada (en adelante
auxList ) de elementos insertados en el montón, cada uno de los cuales se considerará como la raíz de un montón de emparejamiento independiente. Entonces:
- Inserción de nodo diferido en Heap de emparejamiento:
Al insertar el nodo U especificado en el Heap de emparejamiento { R_1 , V_1 }, lo colocamos en auxList, después del encabezado de la lista:
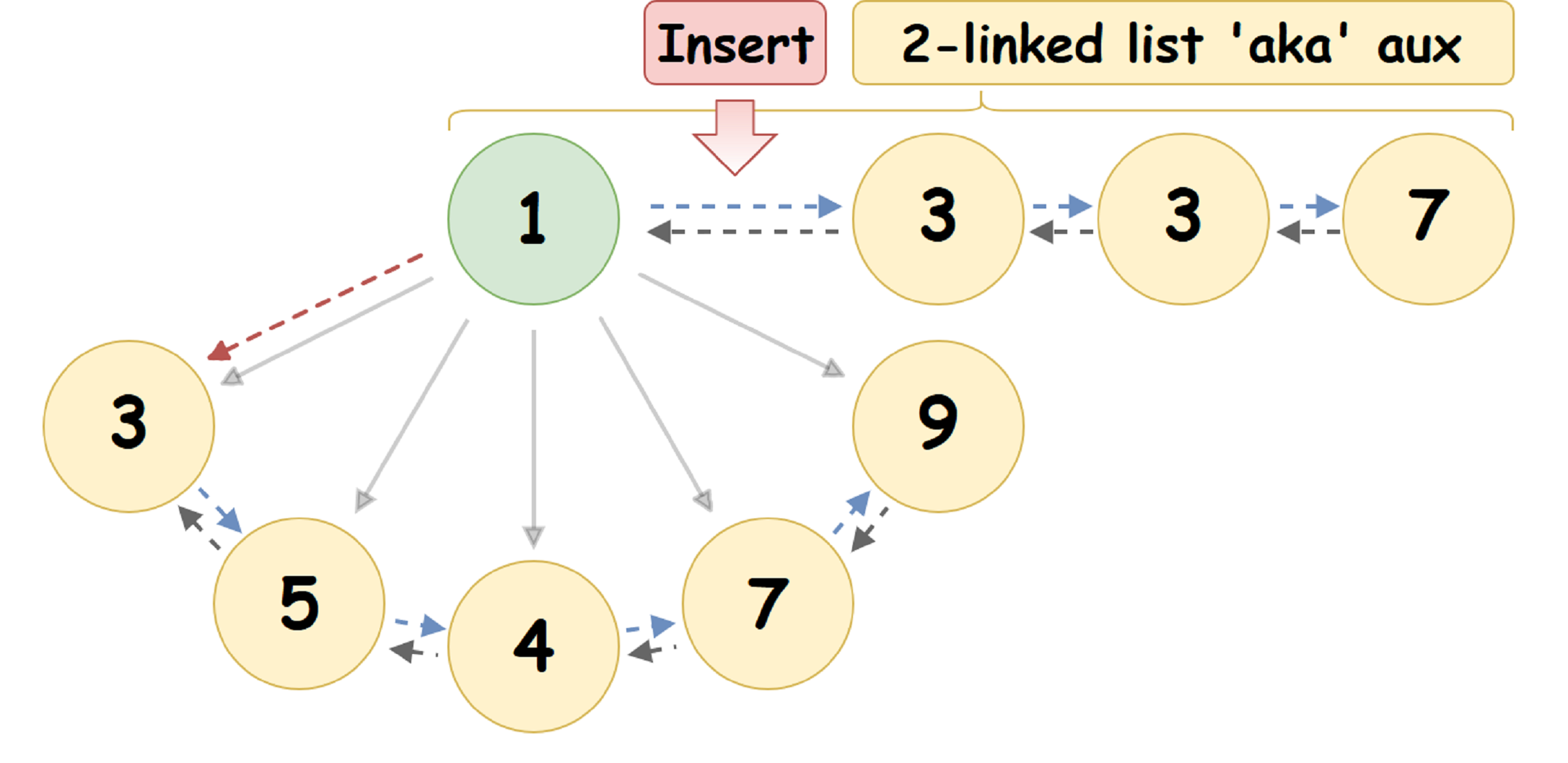
- La fusión perezosa de dos pares de pares:
Lazy Fusiona dos pares de emparejamiento, similar a la inserción del nodo Lazy, donde el nodo insertado es la raíz (cabeza de la lista auxiliar doblemente conectada) de uno de los montones. - Lazy obtiene el elemento mínimo de Heap de emparejamiento:
Al solicitar un mínimo, pasamos por auxList a la lista de raíces de Heap Pairing Heap independientes, combinando por pares los elementos de esta lista con la operación de fusión, y devolvemos el valor de la raíz que contiene el elemento mínimo a uno de los Heap Pairing Heap. - Eliminación diferida del elemento mínimo de emparejamiento de emparejamiento:
Al solicitar la eliminación del elemento mínimo especificado por el Heap de emparejamiento, primero encontramos el nodo que contiene el elemento mínimo, y luego lo eliminamos del árbol en el que está la raíz, insertando sus subárboles en la lista auxiliar del montón principal. - Eliminación diferida de un nodo de emparejamiento de emparejamiento no raíz arbitrario:
Al eliminar un nodo de emparejamiento de emparejamiento no raíz arbitrario, el nodo se elimina del montón y sus nodos secundarios se insertan en la lista auxiliar del montón principal.
En realidad, el uso de la implementación de Lazy Pairing Heap reduce el costo amortizado de inserción y eliminación de nodos arbitrarios en el Pairing Heap: de O (log N) a O (1).
Eso es todo, y debajo encontrará una lista de enlaces y recursos útiles:
[0] Página de JeMalloc Github[1] Artículo original sobre emparejamiento de montones[2] Artículo original sobre montones de emparejamiento de implementación diferida[3] Canal de Telegram sobre optimizaciones de código, C ++, Asm, 'bajo nivel' ¡y nada más que eso!Continuará ...