A. A. A. A. A. A. A.
¿Has pensado en la influencia del metro más cercano al precio de tu piso? A.
A. A. ¿Qué pasa con varios jardines de infancia alrededor de su apartamento? ¿Estás listo para sumergirte en el mundo de los datos geoespaciales?
A. 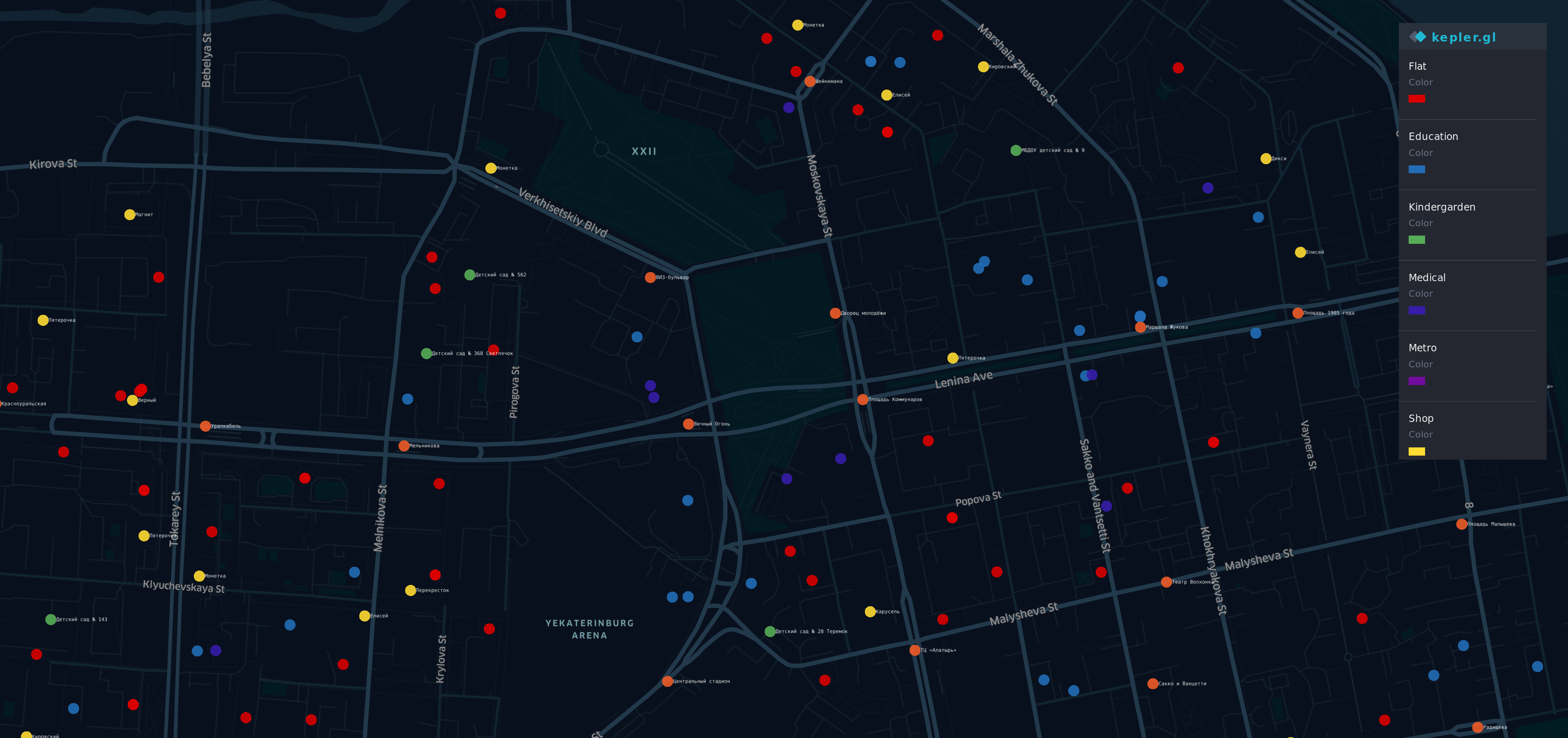 A.
A.
A. A.
A.
¿De qué se trata todo esto?
A.
En la parte anterior , teníamos algunos datos e intentamos encontrar una oferta lo suficientemente buena en un mercado inmobiliario en Ekaterimburgo.
Habíamos llegado a un punto en el que teníamos una precisión en la validación cruzada cercana al 73%. Sin embargo, cada moneda tiene 2 lados. Y el 73% de precisión es el 27% de error. ¿Cómo podríamos hacer eso menos? ¿Cuál es el siguiente paso?
A.
Los datos espaciales están llegando a ayudar
¿Qué pasa con la obtención de más datos del entorno? Podemos usar el contexto geográfico y algunos datos espaciales.
A.
Raramente las personas pasan toda su vida en casa. A. A veces van a las tiendas, sacan a los niños de la guardería. Sus hijos crecen y van a la escuela, la universidad, etc. A.
O ... a veces necesitan ayuda médica y buscan un hospital. Y una cosa muy importante es el transporte público, al menos el metro. A. En otras palabras, hay muchas cosas cerca que tienen un impacto en los precios.
Déjame mostrarte una lista de ellos:
- Paradas de transporte público
- Tiendas
- Jardines de infancia
- Hospitales / instituciones médicas A. A. A. A. A. A. A. A. A.
- Instituciones educativas A. A. A. A. A. A. A. A. A.
- Metro
Visualización de nuevos datos.
Después de obtener esa información de A. Diferentes fuentes A. A. Hice una visualización.
A.
A.  A. A. A. A.
A. A. A. A.
Hay algunos puntos en el mapa del distrito más prestigioso (y caro) de Yek aterinburg. A. A. A. A. A.
A. A.
- A. A. A. A. Puntos R ed - pisos
- O corrió ge - se detiene
- Y ellow - tiendas
- G reen - jardines de infancia
- B lue - educación
- Yo ndigo - médico
- V iolet - Metro
Sí, un arcoíris está aquí.
Resumen
Ahora tenemos un conjunto de datos que está limitado con geodatos y tiene información nueva
df.head(10)

df.describe()

Un buen viejo modelo
Intenta de la misma manera que antes
y = df.cost X = df.drop(columns=['cost']) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,random_state=42)
Luego entrenamos nuestro modelo nuevamente, cruzamos los dedos e intentamos predecir el precio del piso nuevamente.
from sklearn.linear_model import LinearRegression regressor = LinearRegression() model = regressor.fit(X_train, y_train) do_cross_validation(X_test, y_test, model)

Hmm ... se ve mejor que el resultado anterior con un 73% de precisión.
¿Qué pasa con el intento de interpretación? Nuestro modelo anterior tenía la capacidad suficiente para explicar el precio fijo.
estimate_model(regressor)

Vaya ... Nuestro nuevo modelo funciona bien con las características antiguas, pero el comportamiento con las nuevas parece extraño.
Por ejemplo, el mayor número de instituciones educativas o médicas conduce a una disminución en el precio del piso. En consecuencia, el número de paradas cercanas al piso es una situación idéntica y debería obtener una contribución adicional al precio fijo.
El nuevo modelo es más preciso, pero no se ajusta a la vida real.
Algo esta roto
Consideremos lo que pasó.
En primer lugar, quiero recordarles que la característica clave de nuestra regresión lineal es ... erm ... linealidad. Sí, el Capitán Obvio está aquí.
Si sus datos son compatibles con una idea "Cuanto más grande / arrendamiento es X, más grande / arrendamiento será Y" - la regresión lineal será una buena herramienta. Pero los geodatos son más complejos de lo que esperábamos.
Por ejemplo:
- Cuando cerca de su piso hay una parada de autobús, es bueno, pero si la cantidad es de alrededor de 5, conduce a una calle ruidosa y a la gente le gustaría evitar comprar un piso cerca.
- Si hay una universidad, debería tener una buena influencia en el precio,
al mismo tiempo, una multitud de estudiantes cerca de su casa no está tan contenta si no es una persona muy sociable. - El metro cerca de tu casa es bueno, pero si vives en una hora a pie
desde el metro más cercano, no debería tener sentido.
Como puede ver, depende de muchos factores y puntos de vista. Y la naturaleza de nuestros geodatos no es lineal, no podemos extrapolar el impacto de ellos.
Al mismo tiempo, ¿por qué el modelo con coeficientes extraños funciona mejor que el anterior?
plot.figure(figsize=(10,10)) corr = df.corr()*100.0 sns.heatmap(corr[['cost']], cmap= sns.diverging_palette(220, 10), center=0, linewidths=1, cbar_kws={"shrink": .7}, annot=True, fmt=".2f")

Se ve interesante Hemos visto una imagen similar en la parte anterior.
Hay una correlación negativa entre la distancia al metro más cercano y el precio. Y este factor tiene un impacto en la precisión más que algunos anteriores.
Mientras tanto , nuestro modelo funciona desordenado y no ve dependencias entre los datos agregados y la variable de destino. La simplicidad de la regresión lineal tiene sus propios límites. A.
El rey está muerto, ¡viva el rey!
Y si una regresión lineal no es adecuada para nuestro caso, ¿qué puede ser mejor? Si tan solo nuestro modelo pudiera ser "más inteligente" ...
Afortunadamente, tenemos un enfoque que debería ser mejor debido a que es más ... flexible y tiene un mecanismo incorporado "hacer si eso, hacer esto, hacer eso".
El árbol de decisión aparece en la escena.
from sklearn.tree import DecisionTreeRegressor A decision tree can have a different depth, usually, it works well when depth is 3 and bigger. And the parameter of max depth has the biggest influence on the result. Let's do some code for checking depth from 3 to 32 data = [] for x in range(3,32): regressor = DecisionTreeRegressor(max_depth=x,random_state=42) model = regressor.fit(X_train, y_train) accuracy = do_cross_validation(X, y, model) data.append({'max_depth':x,'accuracy':accuracy}) data = pd.DataFrame(data) ax = sns.lineplot(x="max_depth", y="accuracy", data=data) max_result = data.loc[data['accuracy'].idxmax()] ax.set_title(f'Max accuracy-{max_result.accuracy}\nDepth {max_result.max_depth} ')

Bueno ... para una situación cuando el m A. Ax_depth de un árbol es igual a 8, la precisión es superior a 77.
Y sería un buen logro si no pensáramos en los límites de ese enfoque. Eche un vistazo a cómo funcionará con A. A. M ax_depht = 2 A. A. A.
from IPython.core.display import Image, SVG from sklearn.tree import export_graphviz from graphviz import Source 2_level_regressor = DecisionTreeRegressor(max_depth=2, random_state=42) model = 2_level_regressor.fit(X_train, y_train) graph = Source(export_graphviz(model, out_file=None , feature_names=X.columns , filled = True)) SVG(graph.pipe(format='svg'))

En esta imagen, podemos ver que solo hay 4 variantes de predicción. Cuando usa DecisionTreeRegressor , funciona de manera diferente a la Regresión lineal . Simplemente diferente No utiliza una contribución de factores (coeficientes), en lugar de ese DecisionTreeRegressor usa "probabilidad". Y el precio de un piso será el mismo que tiene el piso más similar al previsto.
Podemos mostrarlo prediciendo nuestro precio con ese árbol.
y = two_level_regressor.predict(X_test) errors = pd.DataFrame(data=y,columns=['errors']) f, ax = plot.subplots(figsize=(12, 12)) sns.countplot(x="errors", data=errors)

Y cada predicción coincidirá con uno de estos valores. Y cuando estamos usando max_depth = 8, no podemos esperar más de 256 opciones diferentes para más de 2000 pisos. Quizás sea bueno para los problemas de clasificación, pero no es lo suficientemente flexible para nuestro caso.
Sabiduría de multitud
Si intenta predecir el puntaje en la final de la Copa del Mundo, existe una gran probabilidad de que se equivoque. Al mismo tiempo, si pides opinión a todos los jueces del Campeonato, tendrás más posibilidades de adivinar. Si pregunta a expertos independientes, entrenadores, jueces y luego hace un poco de magia con las respuestas, sus posibilidades aumentarán significativamente. Parece una elección de presidente.
Un conjunto de varios árboles "primitivos" puede dar más que cada uno de ellos. Y rando mForestRegressor es una herramienta que usaremos
En primer lugar, consideremos los parámetros básicos: max_depth , max_features y varios árboles en el modelo.
A.
Numero de arboles
De acuerdo con "¿Cuántos árboles hay en un bosque aleatorio?" La mejor opción será 128 árboles . El aumento adicional del número de árboles no conduce a una mejora significativa en la precisión, sino que aumenta el tiempo para el entrenamiento.
Máximo número de funciones
En este momento nuestro modelo tiene 12 características. La mitad de ellos son viejos que están relacionados con características de plano, otros relacionados con el contexto geográfico. Así que decidí darle una oportunidad a cada uno de ellos. Deje que sean 6 características para un árbol.
Profundidad máxima de un árbol.
Para ese parámetro, podemos analizar una curva de aprendizaje.
from sklearn.ensemble import RandomForestRegressor data = [] for x in range(1,32): regressor = RandomForestRegressor(random_state=42, max_depth=x, n_estimators=128,max_features=6)model = regressor.fit(X_train, y_train)accuracy = do_cross_validation(X, y, model) data.append({'max_depth':x,'accuracy':accuracy}) data = pd.DataFrame(data) f, ax = plot.subplots(figsize=(10, 10)) sns.lineplot(x="max_depth", y="accuracy", data=data) max_result = data.loc[data['accuracy'].idxmax()] ax.set_title(f'Max accuracy-{max_result.accuracy}\nDepth {max_result.max_depth} ')

Whoa ... más del 86% de precisión en max_depth = 16 contra 77% en un árbol de diseño. Se ve increíble, ¿no?
Conclusión
Bueno ... ahora tenemos un mejor resultado en predicción que los anteriores, el 86% está cerca de la línea de meta. El último paso para verificar: veamos la importancia de la función. ¿Los geodatos le dieron algún beneficio a nuestro modelo?
feat_importances = model.feature_importances_ feat_importances = pd.Series(feat_importances, index=X.columns) feat_importances.nlargest(5).plot(kind='barh')

Algunas características antiguas todavía han afectado el resultado. Al mismo tiempo, la distancia al metro y jardines de infancia más cercanos también se ha visto afectada. Y suena lógico.
Sin duda, los geodatos nos ayudaron a mejorar nuestro modelo.
Gracias por leer!
PS
Nuestro viaje aún no ha terminado. El 86% de precisión es un resultado tremendo para datos reales. Mientras tanto, aquí hay una pequeña brecha entre el 14% y el 10% del error medio, que esperamos. En el próximo capítulo de nuestra historia, intentaremos superar esta barrera o al menos disminuir este error. A. A. A. A. A. A. A. A.
Está el portátil IPython