Ecuación de Navier-Stokes y simulación de fluidos en CUDA

Hola Habr En este artículo, trataremos la ecuación de Navier-Stokes para un fluido incompresible, lo resolveremos numéricamente y haremos una hermosa simulación que funciona mediante computación paralela en CUDA. El objetivo principal es mostrar cómo puede aplicar las matemáticas subyacentes a la ecuación en la práctica al resolver el problema de modelar líquidos y gases.




Nota: si está leyendo el Habr desde un dispositivo móvil y no ve las fórmulas, use la versión completa del sitio

Ecuación de Navier-Stokes para un fluido incompresible

$$

$${\ partial {\ bf \ vec {u}} \ over {\ partial t}} = - ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}} - {1 \ over \ rho} \ nabla {\ bf p} + \ nu \ nabla ^ 2 {\ bf \ vec {u}} + {\ bf \ vec {F}}$$

Creo que todos al menos una vez escucharon acerca de esta ecuación, algunos, quizás incluso resolvieron analíticamente sus casos particulares, pero en términos generales, este problema sigue sin resolverse hasta ahora. Por supuesto, no establecemos el objetivo de resolver el problema del milenio en este artículo, sin embargo, aún podemos aplicarle el método iterativo. Pero para empezar, veamos la notación en esta fórmula.

Convencionalmente, la ecuación de Navier-Stokes se puede dividir en cinco partes:

• $$$\ partial {\ bf \ vec {u}} \ over \ partial t$ - denota la tasa de cambio de la velocidad del fluido en un punto (lo consideraremos para cada partícula en nuestra simulación).
• $$$- ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}}$ - el movimiento de fluidos en el espacio.
• $$$- {1 \ over \ rho} \ nabla {\ bf p}$ Es la presión ejercida sobre la partícula (aquí $$$\ rho$ - coeficiente de densidad del fluido).
• $$$\ nu \ nabla ^ 2 {\ bf \ vec {u}}$ - viscosidad del medio (cuanto más grande es, más fuerte es el líquido que resiste la fuerza aplicada a su parte), $$$\ nu$ - coeficiente de viscosidad).
• $$$\ bf \ vec {F}$ - fuerzas externas que aplicamos al fluido (en nuestro caso, la fuerza desempeñará un papel muy específico: reflejará las acciones realizadas por el usuario).

Además, dado que consideraremos el caso de un fluido incompresible y homogéneo, tenemos otra ecuación: $$${{\ \ nabla \ cdot \ bf \ vec {u}} = 0}$ . La energía en el medio ambiente es constante, no va a ninguna parte, no viene de ninguna parte.

Sería un error privar a todos los lectores que no están familiarizados con el análisis vectorial , por lo que al mismo tiempo, revise brevemente todos los operadores que están presentes en la ecuación (sin embargo, recomiendo recordar cuáles son la derivada, el diferencial y el vector, ya que subyacen a todo eso). lo que se discutirá a continuación).

Comenzamos con el operador nabla, que es un vector de este tipo (en nuestro caso, será de dos componentes, ya que modelaremos el fluido en un espacio bidimensional):

$$

$$\ nabla = {\ begin {pmatrix} {\ partial \ over \ partial x}, {\ partial \ over \ partial y} \ end {pmatrix}}$$

El operador nabla es un operador diferencial de vectores y puede aplicarse tanto a una función escalar como a una función vectorial. En el caso de un escalar, obtenemos el gradiente de la función (el vector de sus derivadas parciales) y, en el caso de un vector, la suma de las derivadas parciales a lo largo de los ejes. La característica principal de este operador es que a través de él puede expresar las operaciones principales del análisis vectorial: grad ( gradiente ), div ( divergencia ), podredumbre ( rotor ) y $$$\ nabla ^ 2$ ( Operador de Laplace ). Vale la pena señalar de inmediato que la expresión $$$({\ bf \ vec {u} \ cdot \ nabla}) {\ bf \ vec {u}}$ no es equivalente a $$$({\ nabla \ cdot \ bf \ vec {u}}) {\ bf \ vec {u}}$ - el operador nabla no tiene conmutatividad.

Como veremos más adelante, estas expresiones se simplifican notablemente cuando se mueven a un espacio discreto en el que realizaremos todos los cálculos, así que no se alarme si en este momento no tiene muy claro qué hacer con todo esto. Después de dividir la tarea en varias partes, resolveremos sucesivamente cada una de ellas y presentaremos todo esto en forma de la aplicación secuencial de varias funciones a nuestro entorno.

Solución numérica de la ecuación de Navier-Stokes

Para representar nuestro fluido en el programa, necesitamos obtener una representación matemática del estado de cada partícula de fluido en un punto arbitrario en el tiempo. El método más conveniente para esto es crear un campo vectorial de partículas que almacenen su estado en forma de un plano de coordenadas:



En cada celda de nuestra matriz bidimensional, almacenaremos la velocidad de las partículas a la vez $$$t: {\ bf \ vec {u}} = u ({\ bf \ vec {x}}, t), \ bf \ vec {x} = \ begin {pmatrix} x, y \ end {pmatrix}$ , y la distancia entre partículas se denota por $$$\ delta x$ y $$$\ delta y$ en consecuencia En el código, será suficiente para nosotros cambiar el valor de la velocidad en cada iteración, resolviendo un conjunto de varias ecuaciones.

Ahora expresamos el gradiente, la divergencia y el operador de Laplace teniendo en cuenta nuestra cuadrícula de coordenadas ( $$$i, j$ - índices en la matriz, $$$\ bf \ vec {u} _ {(x)}, \ vec {u} _ {(y)}$ - tomando los componentes correspondientes del vector):

Podemos simplificar aún más las fórmulas discretas de los operadores de vectores si suponemos que $$$\ delta x = \ delta y = 1$ . Esta suposición no afectará en gran medida la precisión del algoritmo, sin embargo, reduce el número de operaciones por iteración y, en general, hace que las expresiones sean más agradables a la vista.

Movimiento de partículas

Estas declaraciones solo funcionan si podemos encontrar las partículas más cercanas en relación con la que se está considerando en este momento. Para anular todos los costos posibles asociados con su búsqueda, no rastrearemos su movimiento, sino de dónde provienen las partículas al comienzo de la iteración proyectando la trayectoria del movimiento hacia atrás en el tiempo (en otras palabras, reste el vector de velocidad multiplicado por el cambio de tiempo desde posición actual). Usando esta técnica para cada elemento de la matriz, nos aseguraremos de que cualquier partícula tenga "vecinos":



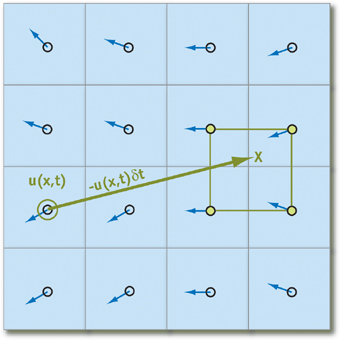
Poniendo eso $$$q$ - un elemento de matriz que almacena el estado de la partícula, obtenemos la siguiente fórmula para calcular su estado a lo largo del tiempo $$$\ delta t$ (creemos que todos los parámetros necesarios en forma de aceleración y presión ya se han calculado):

$$

$$q ({{\ \ vec {\ bf x}}, t + \ delta t}) = q ({{\ \ bf \ vec {x}} - {\ bf \ vec {u}} \ delta t}, t) $$$

Notamos de inmediato que para lo suficientemente pequeño $$$\ delta t$ y nunca podemos ir más allá de los límites de la célula, por lo tanto, es muy importante elegir el momento correcto que el usuario dará a las partículas.

Para evitar la pérdida de precisión en el caso de que una proyección golpee el límite de la celda o en el caso de coordenadas no enteras, realizaremos la interpolación bilineal de los estados de las cuatro partículas más cercanas y la tomaremos como el valor verdadero en el punto. En principio, dicho método prácticamente no reducirá la precisión de la simulación y, al mismo tiempo, es bastante simple de implementar, por lo que lo utilizaremos.

Viscosidad

Cada líquido tiene una cierta viscosidad, la capacidad de evitar la influencia de fuerzas externas en sus partes (la miel y el agua serán un buen ejemplo, en algunos casos sus coeficientes de viscosidad difieren en un orden de magnitud). La viscosidad afecta directamente la aceleración adquirida por el líquido, y puede expresarse mediante la siguiente fórmula, si por brevedad omitimos otros términos por un tiempo:

$$

$${\ partial \ vec {\ bf u} \ over \ partial t} = {\ nu \ nabla ^ 2 \ bf \ vec {u}}$$

. En este caso, la ecuación iterativa para velocidad toma la siguiente forma:

$$

$$u ({\ bf \ vec {x}}, t + \ delta t) = u ({\ bf \ vec {x}}, t) + \ nu \ delta t \ nabla ^ 2 \ bf \ vec {u }$$

Transformaremos ligeramente esta igualdad, llevándola a la forma $$$\ bf A \ vec {x} = \ vec {b}$ (forma estándar de un sistema de ecuaciones lineales):

$$

$$({\ bf I} - \ nu \ delta t \ nabla ^ 2) u ({\ bf \ vec {x}}, t + \ delta t) = {u ({\ bf \ vec {x}}, t )}$$

donde $$$\ bf I$ Es la matriz de identidad. Necesitamos tales transformaciones para aplicar posteriormente el método de Jacobi para resolver varios sistemas de ecuaciones similares. También lo discutiremos más tarde.

Fuerzas externas

El paso más simple del algoritmo es la aplicación de fuerzas externas al medio. Para el usuario, esto se reflejará en forma de clics en la pantalla con el mouse o su movimiento. La fuerza externa se puede describir mediante la siguiente fórmula, que aplicamos para cada elemento de la matriz ( $$$\ vec {\ bf G}$ - vector de impulso $$$x_p, y_p$ - posición del mouse $$$x, y$ - coordenadas de la celda actual, $$$r$ - radio de acción, parámetro de escala):

$$

$$\ vec {\ bf F} = \ vec {\ bf G} \ delta t {\ bf exp} \ left (- {{(x - x_p) ^ 2 + (y - y_p) ^ 2} \ over r} \ right)$$

Un vector de impulso puede calcularse fácilmente como la diferencia entre la posición anterior del mouse y la actual (si existiera), y aquí todavía puede ser creativo. Es en esta parte del algoritmo que podemos introducir la adición de colores a un líquido, su iluminación, etc. Las fuerzas externas también pueden incluir la gravedad y la temperatura, y aunque no es difícil implementar tales parámetros, no los consideraremos en este artículo.

Presión

La presión en la ecuación de Navier-Stokes es la fuerza que impide que las partículas llenen todo el espacio disponible después de aplicarles una fuerza externa. Inmediatamente, su cálculo es muy difícil, pero nuestro problema puede simplificarse enormemente aplicando el teorema de descomposición de Helmholtz .

Llamar $$$\ bf \ vec {W}$ campo vectorial obtenido después de calcular el desplazamiento, las fuerzas externas y la viscosidad. Tendrá divergencia distinta de cero, lo que contradice la condición de incompresibilidad del líquido ( $$$\ nabla \ cdot \ bf \ vec {u} = 0$ ), y para solucionar esto, es necesario calcular la presión. De acuerdo con el teorema de descomposición de Helmholtz, $$$\ bf \ vec {W}$ se puede representar como la suma de dos campos:

$$

$$\ bf \ vec {W} = \ vec {u} + \ nabla p$$

donde $$$\ bf u$ - este es el campo vectorial que estamos buscando con divergencia cero. No se proporcionará ninguna prueba de esta igualdad en este artículo, pero al final puede encontrar un enlace con una explicación detallada. Podemos aplicar el operador nabla a ambos lados de la expresión para obtener la siguiente fórmula para calcular el campo de presión escalar:

$$

$$\ nabla \ cdot \ bf \ vec {W} = \ nabla \ cdot (\ vec {u} + \ nabla p) = \ nabla \ cdot \ vec {u} + \ nabla ^ 2 p = \ nabla ^ 2 p $$$

La expresión escrita arriba es la ecuación de Poisson para la presión. También podemos resolverlo mediante el método de Jacobi mencionado anteriormente, y así encontrar la última variable desconocida en la ecuación de Navier-Stokes. En principio, los sistemas de ecuaciones lineales pueden resolverse en una variedad de formas diferentes y sofisticadas, pero aún nos detendremos en las más simples, para no cargar más este artículo.

Límite y condiciones iniciales

Cualquier ecuación diferencial modelada en un dominio finito requiere condiciones iniciales o límites correctamente especificadas, de lo contrario es muy probable que obtengamos un resultado físicamente incorrecto. Las condiciones límite se establecen para controlar el comportamiento del fluido cerca de los bordes de la cuadrícula de coordenadas, y las condiciones iniciales especifican los parámetros que tienen las partículas en el momento en que comienza el programa.

Las condiciones iniciales serán muy simples: inicialmente el fluido es estacionario (la velocidad de las partículas es cero) y la presión también es cero. Las condiciones de contorno se establecerán para la velocidad y la presión mediante las fórmulas dadas:

$$

$${\ bf \ vec {u} _ {0, j} + \ bf \ vec {u} _ {1, j} \ over 2 \ delta y} = 0, {\ bf \ vec {u} _ {i , 0} + \ bf \ vec {u} _ {i, 1} \ over 2 \ delta x} = 0$$

$$

$${\ bf p_ {0, j} - \ bf p_ {1, j} \ over \ delta x} = 0, {\ bf p_ {i, 0} - \ bf p_ {i, 1} \ over \ delta y} = 0$$

Por lo tanto, la velocidad de las partículas en los bordes será opuesta a la velocidad en los bordes (por lo tanto, se repelerán desde el borde), y la presión es igual al valor inmediatamente al lado del límite. Estas operaciones deben aplicarse a todos los elementos delimitadores de la matriz (por ejemplo, hay un tamaño de cuadrícula $$$N \ veces M$ , luego aplicamos el algoritmo para las celdas marcadas en azul en la figura):

Tinte

Con lo que tenemos ahora, ya puedes encontrar muchas cosas interesantes. Por ejemplo, para darse cuenta de la propagación del tinte en un líquido. Para hacer esto, solo necesitamos mantener otro campo escalar, que sería responsable de la cantidad de pintura en cada punto de la simulación. La fórmula para actualizar el tinte es muy similar a la velocidad, y se expresa como:

$$

$${\ partial d \ over \ partial t} = {- (\ vec {\ bf u} \ cdot \ nabla) d} + \ gamma \ nabla ^ 2d + S$$

En la formula $$$S$ responsable de reponer el área con un tinte (posiblemente según dónde haga clic el usuario), $$$d$ directamente es la cantidad de tinte en el punto, y $$$\ gamma$ - coeficiente de difusión. Resolverlo no es difícil, ya que todo el trabajo básico sobre la derivación de fórmulas ya se ha llevado a cabo, y es suficiente para hacer algunas sustituciones. La pintura se puede implementar en el código como un color en el formato RGB, y en este caso la tarea se reduce a operaciones con varios valores reales.

Vorticidad

La ecuación de vorticidad no es una parte directa de la ecuación de Navier-Stokes, pero es un parámetro importante para una simulación plausible del movimiento de un tinte en un líquido. Debido al hecho de que estamos produciendo un algoritmo en un campo discreto, así como debido a pérdidas en la precisión de los valores de punto flotante, este efecto se pierde y, por lo tanto, necesitamos restaurarlo aplicando fuerza adicional a cada punto en el espacio. El vector de esta fuerza se designa como $$$\ bf \ vec {T}$ y está determinado por las siguientes fórmulas:

$$

$$\ bf \ omega = \ nabla \ times \ vec {u}$$

$$

$$\ vec {\ eta} = \ nabla | \ omega |$$

$$

$$\ bf \ vec {\ psi} = {\ vec {\ eta} \ over {| \ vec {\ eta} |}}$$

$$

$$\ bf \ vec {T} = \ epsilon (\ vec {\ psi} \ times \ omega) \ delta x$$

$$$\ omega$ existe el resultado de aplicar el rotor al vector de velocidad (su definición se da al comienzo del artículo), $$$\ vec \ eta$ - gradiente del campo escalar de valores absolutos $$$\ omega$ . $$$\ vec \ psi$ representa un vector normalizado $$$\ vec \ eta$ y $$$\ epsilon$ Es una constante que controla qué tan grandes serán los vórtices en nuestro fluido.

Método de Jacobi para resolver sistemas de ecuaciones lineales.

Al analizar las ecuaciones de Navier-Stokes, encontramos dos sistemas de ecuaciones, uno para la viscosidad y el otro para la presión. Se pueden resolver mediante un algoritmo iterativo, que se puede describir mediante la siguiente fórmula iterativa:

$$

$$x ^ {(k + 1)} _ {i, j} = {{x ^ {(k)} _ {i-1, j} + x ^ {(k)} _ {i + 1, j} + x ^ {(k)} _ {i, j-1} + x ^ {(k)} _ {i, j + 1} + \ alpha b_ {i, j}} \ over \ beta}$$

Para nosotros $$$x$ - elementos de matriz que representan un campo escalar o vectorial. $$$k$ - el número de iteración, podemos ajustarlo para aumentar la precisión del cálculo o viceversa para reducirlo y aumentar la productividad.

Para calcular la viscosidad, sustituimos: $$$x = b = \ bf \ vec {u}$ , $$$\ alpha = {1 \ over \ nu \ delta t}$ , $$$\ beta = 4+ \ alpha$ aquí está el parámetro $$$\ beta$ - la suma de los pesos. Por lo tanto, necesitamos almacenar al menos dos campos de velocidad vectorial para leer independientemente los valores de un campo y escribirlos en otro. En promedio, para calcular el campo de velocidad por el método de Jacobi, es necesario realizar 20-50 iteraciones, lo cual es bastante si realizamos cálculos en la CPU.

Para la ecuación de presión, hacemos la siguiente sustitución: $$$x = p$ , $$$b = \ nabla \ bf \ cdot \ vec {W}$ , $$$\ alpha = -1$ , $$$\ beta = 4$ . Como resultado, obtenemos el valor $$$p_ {i, j} \ delta t$ en el punto Pero dado que se usa solo para calcular el gradiente restado del campo de velocidad, se pueden omitir transformaciones adicionales. Para el campo de presión, es mejor realizar 40-80 iteraciones, porque con números más pequeños la discrepancia se hace notable.

Implementación de algoritmo

Implementaremos el algoritmo en C ++, también necesitamos Cuda Toolkit (puede leer cómo instalarlo en el sitio web de Nvidia), así como SFML . Necesitamos CUDA para paralelizar el algoritmo, y SFML se usará solo para crear una ventana y mostrar una imagen en la pantalla (en principio, esto se puede escribir en OpenGL, pero la diferencia en el rendimiento no será significativa, pero el código aumentará en otras 200 líneas).

Kit de herramientas de Cuda

Primero, hablaremos un poco sobre cómo usar Cuda Toolkit para paralelizar tareas. Nvidia proporciona una guía más detallada , por lo que aquí nos restringimos solo a lo más necesario. También se supone que pudo instalar el compilador y que fue capaz de construir un proyecto de prueba sin errores.

Para crear una función que se ejecute en la GPU, primero debe declarar cuántos núcleos queremos usar y cuántos bloques de núcleos debemos asignar. Para esto, Cuda Toolkit nos proporciona una estructura especial: dim3 , que establece de forma predeterminada todos sus valores x, y, z en 1. Al especificarlo como argumento al llamar a la función, podemos controlar el número de núcleos asignados. Como estamos trabajando con una matriz bidimensional, necesitamos establecer solo dos campos en el constructor: x e y :

dim3 threadsPerBlock(x_threads, y_threads); dim3 numBlocks(size_x / x_threads, y_size / y_threads); 

donde size_x y size_y son el tamaño de la matriz que se procesa. La firma y la llamada a la función son las siguientes (el compilador Cuda procesa los corchetes angulares triples):

 void __global__ deviceFunction(); // declare deviceFunction<<<numBlocks, threadsPerBlock>>>(); // call from host 

En la función en sí, puede restaurar los índices de una matriz bidimensional a través del número de bloque y el número de núcleo en este bloque utilizando la siguiente fórmula:

 int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; 

Debe tenerse en cuenta que la función ejecutada en la tarjeta de video debe estar marcada con la etiqueta __global__ , y también devolver nula , por lo que la mayoría de las veces los resultados del cálculo se escriben en la matriz que se pasa como argumento y se asignan previamente en la memoria de la tarjeta de video.

Las funciones CudaMalloc y CudaFree son responsables de liberar y asignar memoria en la tarjeta de video. Podemos operar en punteros al área de memoria que devuelven, pero no podemos acceder a los datos desde el código principal. La forma más fácil de devolver los resultados del cálculo es usar cudaMemcpy , similar a la memoria estándar, pero capaz de copiar datos de una tarjeta de video a la memoria principal y viceversa.

SFML y renderizado de ventanas

Armados con todo este conocimiento, finalmente podemos pasar a escribir código directamente. Para comenzar, creemos el archivo main.cpp y coloquemos todo el código auxiliar para el renderizado de la ventana:


línea al comienzo de la función principal

 std::vector<sf::Uint8> pixelBuffer(FIELD_WIDTH * FIELD_HEIGHT * 4); 

crea una imagen RGBA en forma de una matriz unidimensional con una longitud constante. Lo pasaremos junto con otros parámetros (posición del mouse, diferencia entre cuadros) a la función computeField . Estas últimas, así como varias otras funciones, se declaran en kernel.cu y llaman al código ejecutado en la GPU. Puede encontrar documentación sobre cualquiera de las funciones en el sitio web de SFML, no sucede nada muy interesante en el código del archivo, por lo que no nos detendremos allí por mucho tiempo.

Computación GPU

Para comenzar a escribir código en gpu, primero cree un archivo kernel.cu y defina varias clases auxiliares en él: Color3f, Vec2, Config, SystemConfig :


El atributo __host__ delante del nombre del método significa que el código se puede ejecutar en la CPU, __device__ , por el contrario, obliga al compilador a recopilar el código bajo la GPU. El código declara primitivas para trabajar con vectores de dos componentes, color, configuraciones con parámetros que se pueden cambiar en tiempo de ejecución, así como varios punteros estáticos a matrices, que usaremos como buffers para los cálculos.

cudaInit y cudaExit también se definen de manera bastante trivial:


En la función de inicialización, asignamos memoria para matrices bidimensionales, especificamos una matriz de colores que usaremos para pintar el líquido y también establecemos los valores predeterminados en la configuración. En cudaExit, solo liberamos todos los buffers. Por paradójico que parezca, para almacenar matrices bidimensionales, es más ventajoso utilizar matrices unidimensionales, cuyo acceso se realizará con la siguiente expresión:

 array[y * size_x + x]; // equals to array[y][x] 

Comenzamos la implementación del algoritmo directo con la función de movimiento de partículas. Los campos oldField y newField (el campo de donde provienen los datos y dónde se escriben), el tamaño de la matriz, así como el delta de tiempo y el coeficiente de densidad (utilizados para acelerar la disolución del tinte en el líquido y hacer que el medio no sea muy sensible a la advección, se transfieren a advect acciones del usuario). La función de interpolación bilineal se implementa de manera clásica mediante el cálculo de valores intermedios:


Se decidió dividir la función de difusión de la viscosidad en varias partes: computeDiffusion se llama desde el código principal, que llama a difuso y computeColor un número predeterminado de veces, y luego intercambia la matriz de donde tomamos los datos y aquella donde la escribimos. Esta es la forma más fácil de implementar el procesamiento de datos en paralelo, pero estamos gastando el doble de memoria.

Ambas funciones causan variaciones del método de Jacobi. El cuerpo de jacobiColor y jacobiVelocity verifica de inmediato que los elementos actuales no estén en el borde; en este caso, debemos establecerlos de acuerdo con las fórmulas descritas en la sección Límite y condiciones iniciales .


El uso de la fuerza externa se implementa a través de una única función: applyForce , que toma como argumento la posición del mouse, el color del tinte y el radio de acción. Con su ayuda, podemos dar velocidad a las partículas, así como pintarlas. El exponente fraterno le permite hacer que el área no sea demasiado nítida y al mismo tiempo bastante clara en el radio especificado.


El cálculo de vorticidad ya es un proceso más complejo, por lo que lo implementamos en computeVorticity y applyVorticity , también observamos que para ellos es necesario definir dos operadores de vectores como curl (rotor) y absGradient (gradiente de valores de campo absolutos). Para especificar efectos de vórtice adicionales, multiplicamos $$$y$ componente del vector gradiente en $$$-1$ , y luego normalízalo dividiendo por la longitud (sin olvidar comprobar que el vector no es cero):


El siguiente paso en el algoritmo será el cálculo del campo de presión escalar y su proyección en el campo de velocidad. Para hacer esto, necesitamos implementar 4 funciones: divergencia , que considerará la divergencia de velocidad, jacobiPressure , que implementa el método Jacobi para presión, y computePressure con computePressureImpl , que itera los cálculos de campo:


La proyección se ajusta a dos pequeñas funciones: proyecto y el gradiente que requiere presión. Esto puede decirse la última etapa de nuestro algoritmo de simulación:


Después de la proyección, podemos proceder de forma segura a representar la imagen en el búfer y varios efectos posteriores. La función de pintura copia los colores del campo de partículas en la matriz RGBA. También se implementó la función applyBloom , que resalta el líquido cuando se coloca el cursor sobre él y se presiona el botón del mouse. Por experiencia, esta técnica hace que la imagen sea más agradable e interesante para los ojos del usuario, pero no es necesaria en absoluto.

En el procesamiento posterior, también puede resaltar los lugares donde el fluido tiene la velocidad más alta, cambiar el color según el vector de movimiento, agregar varios efectos, etc., pero en nuestro caso nos limitaremos a un tipo mínimo, porque incluso con él las imágenes son muy fascinantes (especialmente en dinámica) :


Y al final, todavía tenemos una función principal que llamamos desde main.cpp : computeField . Vincula todas las piezas del algoritmo, llamando al código en la tarjeta de video y también copia los datos de gpu a cpu. También contiene el cálculo del vector de impulso y la elección del color del tinte, que pasamos a applyForce :

Conclusión

En este artículo, analizamos un algoritmo numérico para resolver la ecuación de Navier-Stokes y escribimos un pequeño programa de simulación para un fluido incompresible. Quizás no entendimos todas las complejidades, pero espero que el material resulte interesante y útil para usted, y al menos sirvió como una buena introducción al campo del modelado de fluidos.

Como autor de este artículo, agradeceré sinceramente los comentarios y adiciones, y trataré de responder todas sus preguntas en esta publicación.

Material adicional

Puede encontrar todo el código fuente en este artículo en mi repositorio de Github . Cualquier sugerencia de mejora es bienvenida.

El material original que sirvió de base para este artículo, puede leerlo en el sitio web oficial de Nvidia. También presenta ejemplos de la implementación de partes del algoritmo en el lenguaje de sombreadores:
developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

La prueba del teorema de descomposición de Helmholtz y una gran cantidad de material adicional sobre mecánica de fluidos se puede encontrar en este libro (en inglés, ver sección 1.2):
Chorin, AJ y JE Marsden. 1993. Una introducción matemática a la mecánica de fluidos. 3ra ed. Springer

El canal de un YouTube de habla inglesa, que hace contenido de alta calidad relacionado con las matemáticas y la solución de ecuaciones diferenciales en particular (inglés) Videos muy visuales que ayudan a comprender la esencia de muchas cosas en matemáticas y física:
3Blue1Brown -
Ecuaciones diferenciales de YouTube (3Blue1Brown)

También agradezco a WhiteBlackGoose por ayudarme a preparar el material para el artículo.

---

Y al final, una pequeña ventaja: algunas capturas de pantalla hermosas tomadas en el programa: Transmisión


directa (configuración predeterminada)


Whirlpool (radio grande en applyForce)


Wave (alta vorticidad + difusión)

Además, por demanda popular, agregué un video con la simulación: