Hola habrozhiteli! Recientemente entregamos al
libro de Chris Bernhard
Quantum Computing for Real IT . Aquí decidieron compartir un extracto del libro "Algoritmo de Grover y búsqueda de datos"
Estamos entrando en la era del big data. La búsqueda eficiente de conjuntos de datos gigantescos es actualmente una preocupación candente para muchas grandes empresas. El algoritmo de Grover es teóricamente capaz de acelerar la recuperación de datos.
Love Grover inventó su algoritmo en 1996. Al igual que los algoritmos de Deutsch y Simon, tiene una mayor velocidad de ejecución en comparación con los algoritmos clásicos en términos de complejidad de consulta. Sin embargo, no podremos implementar el algoritmo actual de recuperación de datos sin oráculos que puedan hacer sus preguntas. Debemos construir un algoritmo que realice el trabajo del oráculo. Pero antes de comenzar a hablar sobre la implementación del algoritmo de Grover, veamos qué hace y cómo.
Algoritmo de Grover
Imagina que tienes cuatro cartas de juego. Están al revés. Sabes que uno de ellos es un as de gusanos y necesitas encontrarlo. ¿Cuántas cartas tendrás que voltear hasta que sepas dónde está el as de los gusanos?
Si tienes suerte, encontrarás la carta deseada en el primer intento, si no tienes suerte, puedes voltear tres cartas, y ninguna de ellas será un as de gusanos. En el peor de los casos, al dar la vuelta a tres cartas, sabrás con seguridad que la última carta es el as del gusano que estás buscando. Entonces, podemos averiguar dónde está el as cambiando de una a tres cartas. En promedio, debes voltear 2.25 cartas.
Esta es una de las tareas que resuelve el algoritmo de Grover. Antes de comenzar la descripción del algoritmo, reformulamos el problema. Tenemos cuatro secuencias binarias: 00, 01, 10 y 11. Tenemos una función f que devuelve 0 para tres de estas secuencias y 1 para la cuarta secuencia. Necesitamos encontrar la secuencia binaria correspondiente al valor de salida 1. Por ejemplo, podemos obtener los siguientes resultados: f (00) = 0, f (01) = 0, f (10) = 1 yf (11) = 0. Ahora la tarea es es averiguar cuántas veces se debe calcular la función para obtener el resultado f (10) = 1. Aquí simplemente reformulamos el problema reemplazando las cartas de juego con funciones, por lo que la respuesta a esta pregunta ya es conocida: como antes, en promedio será necesario calcular la función 2,25 veces.
Al igual que con todos los algoritmos de consulta de complejidad, construimos un oráculo, una puerta que encapsula una función. El oráculo de nuestro ejemplo, donde solo hay cuatro secuencias binarias, se muestra en la Fig. 9.1.
La cadena para el algoritmo de Grover se muestra en la Fig. 9.2.
El algoritmo realiza dos pasos. En el primero, se invierte el signo de la amplitud de probabilidad, asociado con el lugar que estamos tratando de encontrar. El segundo refuerza esta amplitud de probabilidad. Veamos cómo la cadena hace esto.
Después de la transmisión a través de las válvulas Hadamard, los dos qubits superiores obtienen el estado
y el qubit más bajo tiene un estado
El estado combinado se puede escribir como
Los qubits luego pasan a través de la puerta F. Invierte 0 y 1 en el tercer qubit a la ubicación que estamos tratando de encontrar. Para nuestro caso f (10) = 1 obtenemos
Se puede reescribir como
Como resultado, obtenemos dos qubits superiores, no confundidos con los inferiores, pero con la amplitud de probabilidad
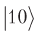
cambiará la señal, indicando la ubicación deseada.
Si medimos los dos qubits superiores en este paso, obtenemos una de las cuatro ubicaciones, y las cuatro respuestas posibles son igualmente probables. Necesitamos dar otro paso: aumentar la amplitud de la probabilidad. La amplificación se lleva a cabo invirtiendo la secuencia de números en relación con su promedio. Si el número está por encima del promedio, cambia y queda por debajo del promedio. Si el número está por debajo del promedio, cambia y se vuelve por encima del promedio. En cada caso, se mantiene la lejanía del promedio. Para ilustrar, usamos cuatro números: 1, 1, 1 y –1. Su suma es 2, y el promedio es 2/4, o 1/2. Luego comenzamos a clasificar los números en la secuencia. El primer número es 1. Está 1/2 por encima del promedio. Después del golpe, debe ser 1/2 más bajo que el promedio. En este caso, se convertirá en 0. El número –1 está por debajo del promedio en 3/2. Después del golpe, debería estar 3/2 por encima del promedio, es decir, convertirse en 2.
Dos qubits superiores tienen actualmente un estado
Girando las amplitudes relativas al promedio, obtenemos

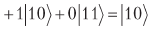
.
Una vez completada la medición, definitivamente obtendremos 10, es decir, una revolución en relación con el promedio nos da exactamente lo que necesitamos. Todo lo que tenemos que hacer es asegurarnos de que haya una puerta o, lo que es lo mismo, una matriz ortogonal que describa una revolución en relación con el promedio. Tal matriz existe:
Como resultado de la acción de la válvula en los dos qubits superiores, obtenemos
En este ejemplo, donde tenemos solo dos qubits, deberíamos usar el oráculo solo una vez. Es suficiente para nosotros hacer la única pregunta. Para el caso n = 2, el algoritmo de Grover da una respuesta exacta después de una sola pregunta, mientras que en el caso clásico, en promedio, se deben hacer 2.25 preguntas.
Esta idea se extiende al caso de un número arbitrario de n qubits. Comenzamos girando el signo de la amplitud de probabilidad, que corresponde a la ubicación deseada. Luego llevamos a cabo una revolución relativa a la media. Sin embargo, en este caso, la amplificación de la amplitud no ocurre tan significativamente como en la situación con dos qubits. Tomemos por ejemplo ocho números, siete de los cuales son 1 y uno es -1. Su suma es 6 y el promedio es 6/8. Después de un giro, el promedio 1 girará 1/2, y –1 girará 10/4. Como resultado, en presencia de tres qubits, midiendo un qubit después de la amplificación de la amplitud, obtendremos la ubicación deseada con mayor probabilidad que otros. El problema es que hay una posibilidad significativa de obtener la respuesta incorrecta. Necesitamos una mayor probabilidad de obtener la respuesta correcta; necesitamos amplificar aún más la amplitud antes de medir. La solución es transferir todos los qubits a través de la cadena. Volteamos nuevamente el signo de la amplitud de probabilidad asociada con la ubicación deseada y volvemos a voltear en relación con el promedio.
Considere el caso generalizado. Necesitamos encontrar algo en una de las m ubicaciones posibles. Para encontrarlo de la manera clásica, en el peor de los casos tenemos que hacer preguntas m - 1. El número de preguntas crece en proporción a m. Grover calculó una fórmula que determina cuántas veces se necesita usar su cadena para obtener la máxima probabilidad de una respuesta correcta. El número que da esta fórmula crece proporcionalmente
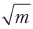
. Esta es la aceleración cuadrática.
Aplicaciones del algoritmo de Grover
Existen varios problemas con la implementación del algoritmo. Primero, la aceleración cuadrática se evalúa en relación con la solicitud de complejidad. Para usar el oráculo, debe crearlo, y si no realiza esta tarea con el debido cuidado, el número de pasos realizados por el oráculo superará el número de pasos que guarda el algoritmo y, como resultado, el algoritmo será más lento en lugar de más rápido que el clásico. Otro problema es que, al determinar la aceleración, suponemos que el conjunto de datos está desordenado. Si el conjunto de datos tiene una estructura específica, a menudo puede encontrar un algoritmo clásico que utiliza esta estructura y busca una solución mucho más rápido. El último problema está relacionado con la aceleración. La aceleración cuadrática no es más que una aceleración exponencial, que observamos en otros algoritmos. ¿Es posible lograr más? Veamos estos problemas.
Ambos problemas asociados con la implementación del oráculo y la presencia de la estructura en el conjunto de datos están justificados y muestran que, en la mayoría de los casos, el algoritmo de Grover no tiene una aplicación práctica para buscar en la base de datos. Pero en algunas situaciones, tener una estructura en los datos hace posible crear un oráculo que actúa con alta eficiencia. En tales situaciones, el algoritmo puede superar a los algoritmos clásicos. Ya se ha dado la respuesta a la pregunta de la posibilidad de lograr un mayor éxito. Está comprobado que el algoritmo de Grover es óptimo. No existe un algoritmo cuántico capaz de resolver un problema con más de una aceleración cuadrática. La aceleración cuadrática, aunque no es tan impresionante como exponencial, todavía ofrece algunos beneficios. Cuando se trabaja con grandes conjuntos de datos, cualquier aceleración puede ser valiosa.
Es probable que el algoritmo de Grover encuentre la aplicación principal no para la búsqueda, como se presentó anteriormente, sino para sus variaciones. En particular, la idea de amplificar la amplitud puede ser útil.
Examinamos solo algunos algoritmos, pero los algoritmos de Shore y Grover se consideran los más importantes. Hay muchos otros algoritmos basados en las ideas inherentes a estos dos.1 Ahora, pasemos nuestra atención de los algoritmos cuánticos a otros campos de aplicación de la computación cuántica.