¿Cómo probar ideas, arquitectura y algoritmos sin escribir código? ¿Cómo formular y verificar sus propiedades? ¿Qué son los verificadores de modelos y los buscadores de modelos? ¿Qué hacer cuando las capacidades de las pruebas no son suficientes?
Hola Mi nombre es Vasil Dyadov, ahora trabajo como programador en Yandex.Mail, antes de trabajar en Intel, estaba desarrollando código RTL (nivel de transferencia de registro) en Verilog / VHDL para ASIC / FPGA incluso antes. Hace tiempo que me gusta el tema de la confiabilidad del software y el hardware, las matemáticas, las herramientas y los métodos utilizados para desarrollar software y lógica con propiedades garantizadas y predefinidas.
Este es el segundo artículo de una serie (el primer artículo aquí ), diseñado para llamar la atención de los desarrolladores y gerentes sobre el enfoque de ingeniería para el desarrollo de software. Recientemente, ha sido ignorado inmerecidamente, a pesar de los cambios revolucionarios en su enfoque y herramientas de apoyo.
El primer artículo les pareció a algunos lectores demasiado abstracto. A muchos les gustaría ver un ejemplo del uso de un enfoque de ingeniería y especificaciones formales en condiciones cercanas a la realidad.
En este artículo, veremos un ejemplo de la aplicación real de TLA + para resolver un problema práctico.
Siempre estoy abierto a discutir temas relacionados con el desarrollo de software, y estaré encantado de conversar con los lectores (las coordenadas para la comunicación están en mi perfil).
¿Qué es TLA +?
Para empezar, quiero decir algunas palabras sobre TLA + y TLC.
TLA + (lógica temporal de acciones + datos) es un formalismo que se basa en un tipo de lógica temporal. Diseñado por Leslie Lamport.
Dentro del marco de este formalismo, se puede describir el espacio de las variantes de comportamiento del sistema y las propiedades de estos comportamientos.
Para simplificar, podemos suponer que el comportamiento del sistema está representado por una secuencia de sus estados (como cuentas infinitas, bolas en una cuerda), y la fórmula TLA + define una clase de cadenas que describen todas las posibles variantes del comportamiento del sistema (una gran cantidad de cuentas).
TLA + es adecuado para describir máquinas interactivas de estado finito no deterministas (por ejemplo, la interacción de servicios en un sistema), aunque su expresividad es suficiente para describir muchas otras cosas (que pueden expresarse en lógica de primer orden).
Y TLC es un verificador de modelos de estado explícito: un programa que, de acuerdo con una descripción dada del sistema TLA + y fórmulas de propiedades, itera sobre los estados del sistema y determina si el sistema satisface las propiedades especificadas.
Típicamente, trabajar con TLA + / TLC se construye de esta manera: describimos el sistema en TLA +, formalizamos propiedades interesantes en TLA +, ejecutamos TLC para verificación.
Como no es fácil describir directamente un sistema más o menos complejo en TLA +, se inventó un lenguaje de nivel superior: PlusCal, que se traduce en TLA +. PlusCal existe de dos maneras: con Pascal y sintaxis tipo C. En el artículo que usé sintaxis tipo Pascal, me parece que es mejor leerlo. PlusCal con respecto a TLA + es más o menos lo mismo que C con respecto al ensamblador.
Aquí no profundizaremos en la teoría. La literatura para la inmersión en TLA + / PlusCal / TLC se proporciona al final del artículo.
Mi tarea principal es mostrar la aplicación de TLA + / TLC en un ejemplo simple y comprensible de la vida real.
En algunos comentarios al artículo anterior, me reprocharon que no pinté los fundamentos teóricos de las herramientas, pero el propósito de esta serie de artículos era mostrar la aplicación práctica de herramientas para el enfoque de ingeniería en el desarrollo de software.
Creo que una inmersión profunda en la teoría es de poco interés para cualquiera, pero si está interesado, siempre puede ir al PM para obtener enlaces y explicaciones, y hasta donde tengo suficiente conocimiento (después de todo, no soy un matemático teórico, sino un ingeniero de software), intentaré responder .
Declaración del problema.
Primero, hablaré un poco sobre la tarea para la que se utilizó TLA +.
La tarea está relacionada con el procesamiento del flujo de eventos. Es decir, crear una cola para almacenar eventos y enviar notificaciones sobre estos eventos.
El almacén de datos se organiza físicamente sobre la base del DBMS PostgreSQL.
Lo principal que debes saber:
- Hay fuentes de eventos. Para nuestros propósitos, podemos limitarnos al hecho de que cada evento se caracteriza por el tiempo en que se planifica su procesamiento. Estas fuentes escriben eventos en la base de datos. Por lo general, el tiempo de escritura en la base de datos y el tiempo del procesamiento planificado no están relacionados de ninguna manera.
- Existen procesos de coordinación que leen eventos de la base de datos y envían notificaciones de eventos futuros a aquellos componentes del sistema que deben responder a estas notificaciones.
- Requisito fundamental: no debemos perder eventos. La notificación del evento en casos extremos puede repetirse, es decir, debe haber una garantía al menos una vez . En los sistemas distribuidos, es extremadamente difícil obtener una garantía solo una vez (incluso puede ser imposible, pero debe probarse) sin mecanismos de consenso, y ellos (al menos todo lo que sé) tienen un efecto muy fuerte en el sistema en términos de retraso y rendimiento.
Ahora algunos detalles:
- Hay muchos procesos fuente; pueden generar millones (en el peor de los casos) de eventos que caen en un intervalo de tiempo estrecho.
- Los eventos se pueden generar tanto para el futuro como para el pasado (por ejemplo, si el proceso de origen se ha ralentizado y registrado un evento por un momento que ya ha pasado).
- La prioridad del procesamiento de eventos está en el tiempo, es decir, primero debemos procesar los primeros eventos.
- Para cada evento, el proceso de origen genera un número aleatorio worker_id , debido a que los eventos se distribuyen entre los coordinadores.
- Existen varios procesos de coordinación (escala según las necesidades en función de la carga del sistema).
- Cada proceso de coordinador procesa eventos para su propio conjunto worker_id , es decir, debido a worker_id, evitamos la competencia entre coordinadores y la necesidad de bloqueos.
Como se puede ver en la descripción, podemos considerar solo un proceso de coordinación y no tener en cuenta worker_id en nuestra tarea.
Es decir, por simplicidad, suponemos que:
- Hay muchos procesos fuente.
- El proceso de coordinación es uno.
Describiré la evolución de la idea de resolver este problema en etapas, para que sea más comprensible cómo evolucionó el pensamiento de una implementación simple a una optimizada.
Decisión de la frente
Crearemos una placa para eventos donde almacenaremos eventos en forma de una marca de tiempo (no estamos interesados en otros parámetros en esta tarea). Construyamos un índice en el campo de marca de tiempo .
Parece ser una solución perfectamente normal.
Solo hay un problema con la escalabilidad: cuantos más eventos, más lentas serán las operaciones de la base de datos.
Los eventos pueden venir en el pasado, por lo que el coordinador tendrá que revisar constantemente toda la línea de tiempo.
El problema se puede resolver ampliamente dividiendo la base de datos en fragmentos por tiempo, etc. Pero esta es una forma de uso intensivo de recursos.
Como resultado, el trabajo de los coordinadores se ralentizará, ya que tendrá que leer y combinar datos de varias bases de datos.
Es difícil implementar el almacenamiento en caché de eventos en el coordinador para no ir a las bases para procesar cada evento.
Más bases de datos: más problemas de tolerancia a fallas.
Y así sucesivamente.
No nos detendremos en esta solución frontal en detalle, ya que es trivial y poco interesante.
Primera optimización
Veamos cómo mejorar la solución frontal.
Para optimizar el acceso a la base de datos, puede complicar un poco el índice, agregar un identificador que aumente de forma monótona a los eventos que se generarán al confirmar una transacción en la base de datos. Es decir, el evento ahora se caracteriza por el par {time, id} , donde time es la hora a la que se programa el evento, id es un contador que aumenta de manera monótona. Hay una garantía de unicidad de id para cada evento, pero no hay garantía de que los valores de id no tengan agujeros (es decir, puede haber una secuencia de este tipo: 1 , 2 , 7 , 15 ).
Parece que ahora podemos almacenar el identificador del último evento de lectura en el proceso del coordinador y, al buscar, seleccionar eventos con identificadores mayores que el último evento procesado.
Pero aquí surge el problema de inmediato: los procesos de origen pueden registrar un evento con una marca de tiempo en el futuro. Luego, tendremos que tener en cuenta constantemente el conjunto de eventos con pequeños identificadores en el proceso de coordinación, cuyo tiempo de procesamiento aún no ha llegado.
Puede notar que los eventos relativos a la hora actual se dividen en dos clases:
- Eventos con una marca de tiempo en el pasado, pero con un identificador grande. Se escribieron en la base de datos recientemente, después de que procesamos ese intervalo de tiempo. Estos son eventos de alta prioridad y deben procesarse primero para que la notificación, que ya llega tarde, ni siquiera llegue tarde.
- Eventos registrados alguna vez con marcas de tiempo cercanas al momento actual. Tales eventos tendrán un valor identificador bajo.
En consecuencia, el estado actual del proceso del coordinador se caracteriza por el par {state.time, state.id}.
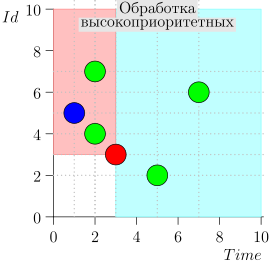
Resulta que los eventos de alta prioridad están a la izquierda y por encima de este punto (región rosa), y los eventos normales están a la derecha (azul claro):
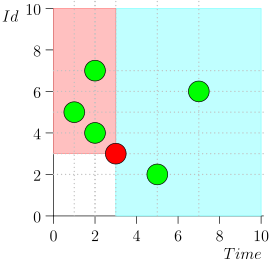
Diagrama de flujo
El algoritmo de trabajo del coordinador es el siguiente:
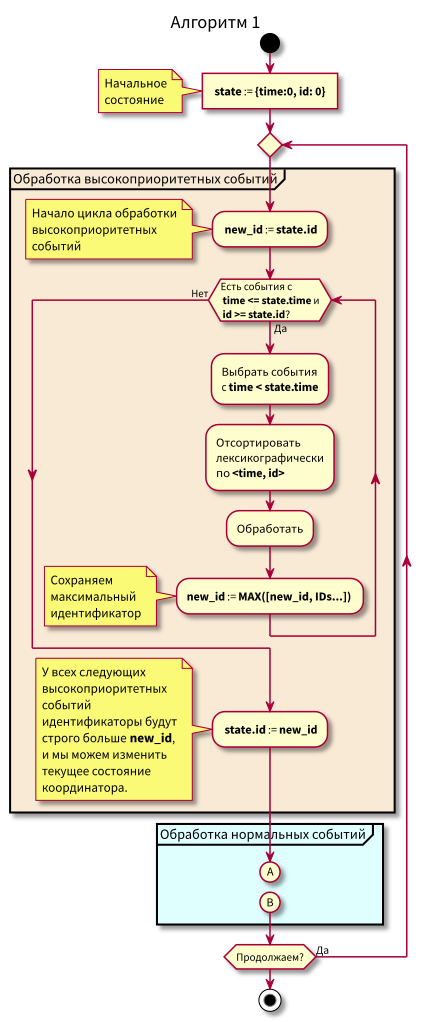
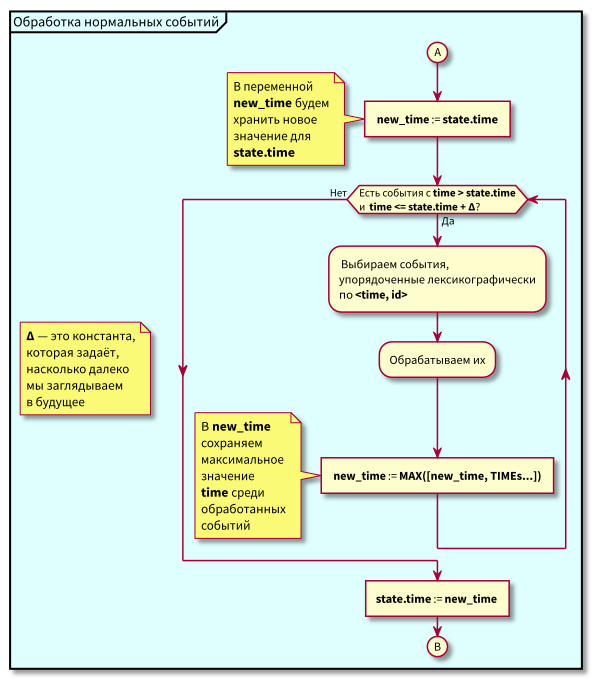
Al estudiar el algoritmo, pueden surgir preguntas:
- ¿Qué pasa si comienza el procesamiento de eventos normales y en ese momento llegan nuevos eventos en el pasado (en la región rosa), ¿no se perderán? Respuesta: se procesarán en el próximo ciclo de procesamiento de eventos de alta prioridad. No pueden perderse, ya que se garantiza que su identificación será más alta que state.id.
- ¿Qué sucede si después de procesar todos los eventos normales, al momento de cambiar al procesamiento de eventos de alta prioridad, llegan nuevos eventos con marcas de tiempo del intervalo [estado.hora, estado.hora + Delta], los perdemos? Respuesta: caerán en el área rosa, ya que tendrán tiempo <state.time e id > state.id: llegaron recientemente y la identificación aumenta de forma monotónica.
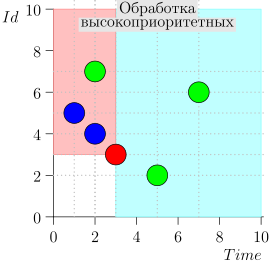
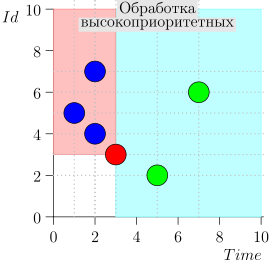
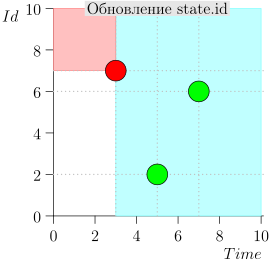
Ejemplo de operación de algoritmo
Veamos algunos pasos del algoritmo:
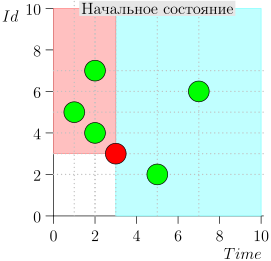
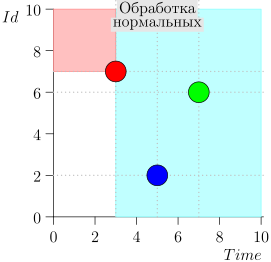
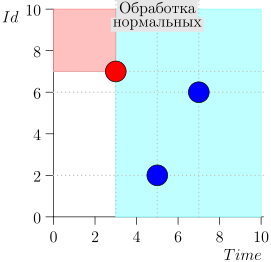
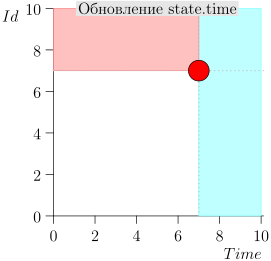
Modelo
Nos aseguraremos de que el algoritmo no pierda eventos y se enviarán todas las notificaciones: redactaremos un modelo simple y lo verificaremos.
Para el modelo usamos TLA +, más precisamente PlusCal, que se traduce en TLA +.
---------------- MODULE events ---------------- EXTENDS Naturals, FiniteSets, Sequences, TLC (* --algorithm Events \* \* (by Daniel Jackson) \* small-scope hypothesis, \* , ́ \* \* \* : \* Events - - , \* [time, id], \* \* \* \* Event_Id - \* id \* MAX_TIME - , \* \* TIME_DELTA - Delta, \* \* variables Events = {}, Event_Id = 0, MAX_TIME = 5, TIME_DELTA \in 1..3 define \* \* ZERO_EVT == [time |-> 0, id |-> 0] MAX(S) == CHOOSE x \in S: \A y \in S: y <= x MIN(S) == CHOOSE x \in S: \A y \in S: y >= x \* fold_left/fold_right RECURSIVE SetReduce(_, _, _) SetReduce(Op(_, _), S, value) == IF S = {} THEN value ELSE LET s == CHOOSE s \in S : TRUE IN SetReduce(Op, S \ {s}, Op(s, value)) (* ( ) *) ToSeq(S) == LET op(e, val) == Append(val, e) IN SetReduce(op, S, << >>) (* : *) ToSet(S) == {S[i] : i \in DOMAIN(S)} (* map *) MapSet(Op(_), S) == {Op(x) : x \in S} (* *) \* id GetIds(Evts) == MapSet(LAMBDA x: x.id, Evts) \* time GetTimes(Evts) == MapSet(LAMBDA x: x.time, Evts) (* SQL *) \* \* ORDER BY EventsOrderByTime(e1, e2) == e1.time < e2.time EventsOrderById(e1, e2) == e1.id < e2.id EventsOrder(e1, e2) == \* time, id \/ EventsOrderByTime(e1, e2) \/ /\ e1.time = e2.time /\ EventsOrderById(e1, e2) \* SELECT * FROM events \* WHERE time <= curr_time AND id >= max_id \* ORDER BY time, id SELECT_HIGH_PRIO(state) == LET \* \* time <= curr_time \* AND id >= maxt_id selected == {e \in Events : /\ e.time <= state.time /\ e.id >= state.id } IN selected \* SELECT * FROM events \* WHERE time > current_time AND time - Time <= delta_time \* ORDER BY time, id SELECT_NORMAL(state, delta_time) == LET selected == {e \in Events : /\ e.time <= state.time + delta_time /\ e.time > state.time } IN selected \* Safety predicate \* ALL_EVENTS_PROCESSED(state) == \A e \in Events: \/ e.time >= state.time \/ e.id >= state.id end define; \* - fair process inserter = "Sources" variable n, t; begin forever: while TRUE do \* get_time: \* \* , , \* with evt_time \in 0..MAX_TIME do t := evt_time; end with; \* ; \* : \* 1. . \* 2. , \* Event_Id - , \* commit: \* either - either Events := Events \cup {[time |-> t, id |-> Event_Id]} || Event_Id := Event_Id + 1; or Event_Id := Event_Id + 1; end either; end while; end process fair process coordinator = "Coordinator" variable state = ZERO_EVT, events = {}; begin forever: while TRUE do \* high_prio: events := SELECT_HIGH_PRIO(state); \* process_high_prio: \* , \* Events, \* state.id := MAX({state.id} \union GetIds(events)) || \* , \* Events := Events \ events || \* events , \* events := {}; \* - normal: events := SELECT_NORMAL(state, TIME_DELTA); process_normal: state.time := MAX({state.time} \union GetTimes(events)) || Events := Events \ events || events := {}; end while; end process end algorithm; *) \* BEGIN TRANSLATION \* TLA+, PlusCal \* END TRANSLATION ================================
Como puede ver, la descripción es relativamente pequeña, a pesar de la sección bastante voluminosa de definiciones (definir), que podría extraerse en un módulo separado y luego reutilizarse.
En los comentarios traté de explicar lo que está sucediendo en el modelo. Espero que esto
Lo logré y no hay necesidad de pintar el modelo con más detalle.
Solo me gustaría aclarar un punto con respecto a la atomicidad de las transiciones entre estados y características de modelado.
El modelado se lleva a cabo realizando pasos atómicos de procesos. En una transición, se realiza un paso atómico de un proceso en el que se puede realizar este paso. La elección del paso y el proceso no es determinista: durante el modelado, se ordenan todas las cadenas posibles de pasos atómicos de todos los procesos.
Puede surgir la pregunta: ¿qué pasa con el modelado del verdadero paralelismo, cuando realizamos simultáneamente varios pasos atómicos en diferentes procesos?
Esta pregunta Leslie Lamport ha sido respondida durante mucho tiempo en el libro Especificando sistemas y otros trabajos.
No citaré la respuesta por completo, en resumen, la esencia es esta: si no hay una escala de tiempo exacta donde cada evento esté vinculado a un momento específico, entonces no hay diferencia en modelar eventos paralelos como eventos secuenciales no deterministas, porque siempre podemos suponer que un evento ocurrió antes que otro valor infinitesimal
Pero lo realmente importante es la asignación competente de los pasos atómicos. Si hay demasiados, se producirá una explosión combinatoria del espacio de estado. Si toma menos pasos de los necesarios, o los selecciona incorrectamente, es decir, la probabilidad de perder un estado / transición no válido (es decir, perderemos los errores en el modelo).
Para dividir correctamente los procesos en pasos atómicos, debe tener una buena idea de cómo funciona el sistema en términos de la dependencia de los procesos de los datos y los mecanismos de sincronización.
Como regla general, dividir los procesos en pasos atómicos no causa grandes problemas. Y si lo hace, entonces indica una falta de comprensión del problema y no problemas con la compilación del modelo y la escritura de la especificación TLA +. Esta es otra característica muy útil de las especificaciones formales: requieren un estudio y análisis exhaustivos.
un problema Como regla general, si la tarea es significativa y bien entendida, no hay problemas con su formalización.
Verificación del modelo
Para modelar usaré TLA-toolbox. Por supuesto, puede ejecutar todo desde la línea de comandos, pero el IDE es aún más conveniente, especialmente para comenzar a aprender sobre modelado usando TLA +.
La creación del proyecto está bien descrita en manuales, artículos y libros, los enlaces a los que he citado al final del artículo, por lo que no me repetiré. Lo único que llamaré su atención es la configuración de simulación.
TLC es un verificador de modelos con verificación explícita de estado. Está claro que el espacio estatal debe estar limitado por límites razonables. Por un lado, debe ser lo suficientemente grande como para poder verificar las propiedades que nos interesan y, por otro lado, lo suficientemente pequeño como para completar la simulación en un tiempo razonable utilizando recursos aceptables.
Este es un punto bastante delicado, aquí debe comprender las propiedades del sistema y el modelo. Pero rápidamente viene con experiencia. Para empezar, simplemente puede establecer los límites máximos posibles que aún son aceptables en términos de tiempo de simulación y recursos consumidos.
También hay un modo de verificar no todo el espacio de estado, sino cadenas selectivas a una cierta profundidad. A veces también es posible y necesario usarlo.
Volvemos a la configuración de simulación.
Primero, definimos las restricciones en el espacio de estado del sistema. Las limitaciones se establecen en la sección Configuración avanzada de simulación de restricciones de estado / Opciones .
Allí indiqué una expresión TLA +: Cardinality(Events) <= 5 /\ Event_Id <= 5 ,
donde Event_Id es el límite superior del valor del identificador de evento, Cardinality(Events) es el tamaño del conjunto de registros de eventos (limitado el modelo base
datos por cinco registros en una placa).
En la simulación, el TLC solo analizará los estados en los que esta fórmula es verdadera.
Todavía puede permitir transiciones de estado válidas ( Opciones avanzadas / Restricción de acción ),
pero no lo necesitamos
A continuación, indicamos la fórmula TLA + que describe nuestro sistema: Descripción general del modelo / Fórmula temporal = Spec , donde Spec es el nombre de la fórmula TLA + autogenerada por PlusCal (en el código del modelo anterior no es: para ahorrar espacio, no cité el resultado de traducir PlusCal a TLA +) .
La siguiente configuración a la que vale la pena prestar atención es la comprobación de punto muerto.
(marca de verificación en Descripción general del modelo / Punto muerto ). Cuando esta bandera está habilitada, el TLC verificará el modelo para los estados "colgantes", es decir, aquellos de los cuales no hay transiciones salientes. Si hay tales estados en el espacio de estados, esto significa un claro error en el modelo. O en TLC, que, como cualquier otro programa no trivial, no es inmune a los errores :) En mi (no tan grande) práctica, todavía no he encontrado puntos muertos.
Y finalmente, en aras de que se iniciaron todas estas pruebas, la fórmula de seguridad en Model Overview / Invariants = ALL_EVENTS_PROCESSED(state) .
TLC verificará la validez de la fórmula en cada estado, y si se vuelve falsa,
mostrará un mensaje de error y mostrará la secuencia de estados que condujeron al error.
Después de iniciar TLC, después de trabajar durante aproximadamente 8 minutos, informó "Sin errores". Esto significa que el modelo se prueba y cumple con las propiedades especificadas.
TLC también muestra muchas estadísticas interesantes. Por ejemplo, para este modelo, se obtuvieron 7 677 824 estados únicos; en total, el TLC analizó 27 109 029 estados, el diámetro del espacio de estado es 47 (esta es la longitud máxima de la cadena de estado antes de la repetición,
duración máxima del ciclo desde estados no repetidos en el gráfico de estado y transición).
Si dividimos 27 millones de estados en 8 minutos, obtenemos aproximadamente 56 mil estados por segundo, lo que puede no parecer muy rápido. Pero tenga en cuenta que ejecuté la simulación en una computadora portátil que funcionaba en modo de ahorro de energía (forcé la frecuencia central a 800 MHz, porque viajaba en ese momento en un tren eléctrico), y no optimicé el modelo para la velocidad de simulación en absoluto.
Hay muchas formas de acelerar la simulación: desde portar parte del código del modelo TLA + a Java y conectarse a TLC sobre la marcha (es útil para acelerar todo tipo de funciones auxiliares) hasta ejecutar TLC en las nubes y en los clústeres (el soporte de la nube de Amazon y Azure está integrado en el propio TLC).
Segunda optimización
En el algoritmo anterior, todo está bien, excepto por algunos problemas:
- Hasta que
[state.time, state.time + Delta] todos los eventos de la zona azul en el intervalo [state.time, state.time + Delta] , no podemos pasar a eventos de alta prioridad. Es decir, los eventos tardíos llegarán tarde aún más. Y generalmente la demora es impredecible. Debido a esto, state.time puede estar muy por detrás de la hora actual, y esta es la causa del siguiente problema. - Los eventos que llegan a la región de eventos normales pueden llegar tarde ( id > state.id). Ya son de alta prioridad y deben considerarse eventos de la región rosa, y todavía los consideramos normales y los tratamos como normales.
- Es difícil organizar el almacenamiento en caché de eventos y la reposición de caché (lectura de la base de datos).
Si los dos primeros puntos son obvios, entonces el tercero probablemente planteará la mayoría de las preguntas. Detengámonos en ello con más detalle.
Supongamos que queremos leer primero un número fijo de eventos en la memoria y luego procesarlos.
Después del procesamiento, queremos marcar eventos en la base de datos con consultas de bloque como procesadas, porque si trabaja no con bloques, sino con eventos individuales, no habrá grandes ganancias con el almacenamiento en caché.
Supongamos que hemos procesado parte de los bloques y queremos complementar el caché. Luego, si llegan eventos tardíos de alta prioridad durante el procesamiento, podemos procesarlos temprano.
Es decir, es muy deseable poder leer eventos en bloques pequeños para procesar los retrasos lo más rápido posible, pero actualizar el atributo de procesamiento en la base de datos con bloques grandes a la vez, para mayor eficiencia.
¿Qué hacer en este caso?
Intente trabajar con la base de datos en pequeños bloques con un área azul y rosa y mueva el punto de estado en pequeños pasos.
Por lo tanto, la memoria caché se introdujo y se leyó desde los datos de la base de datos, después de cada lectura, el punto de estado se cambió para no volver a leer los eventos ya leídos.
Ahora el algoritmo se ha vuelto un poco más complicado, comenzamos a leer en porciones limitadas.
Diagrama de flujo
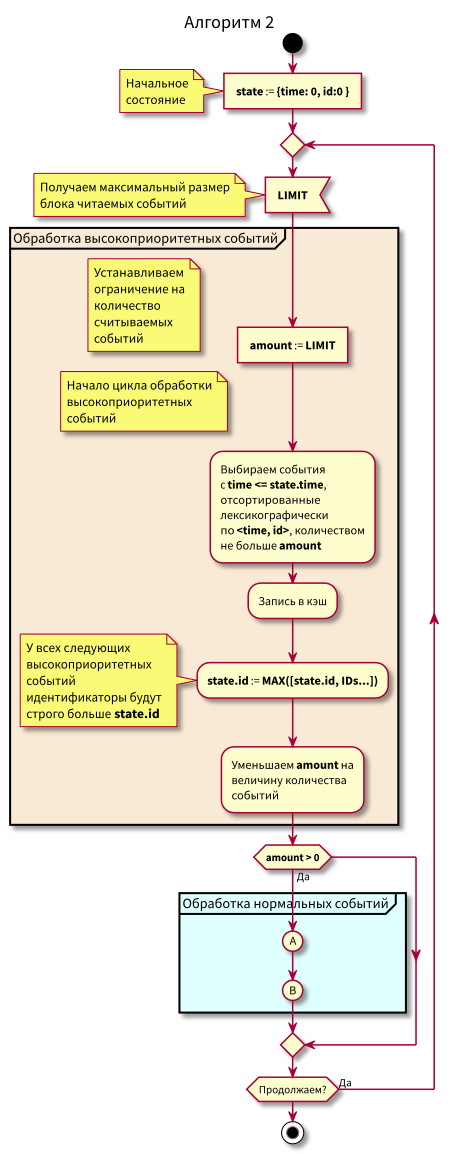
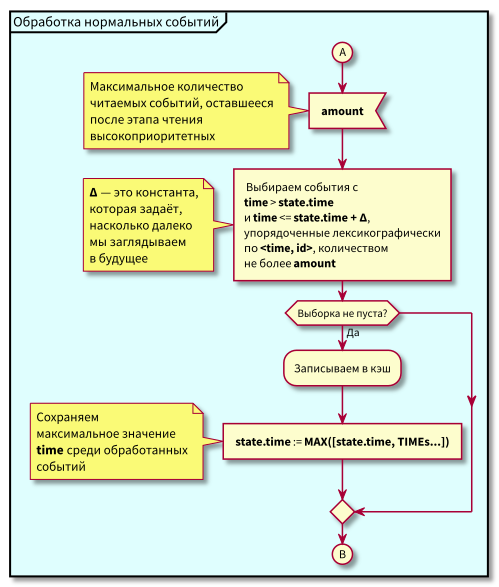
En este algoritmo, se puede ver que debido a la restricción en bloques de eventos legibles, el retraso máximo en la transición del procesamiento de baja prioridad al procesamiento de alta prioridad será igual al tiempo de procesamiento máximo del bloque.
Es decir, ahora podemos leer eventos en la memoria caché en pequeños bloques y controlar el retraso máximo en la transición al procesamiento de eventos de alta prioridad mediante el control del tamaño máximo de bloque para la lectura.
Ejemplo de operación de algoritmo
Veamos el algoritmo en el trabajo, en pasos. Por conveniencia, tome LIMIT = 2 .
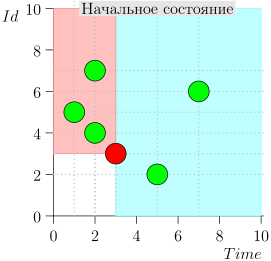
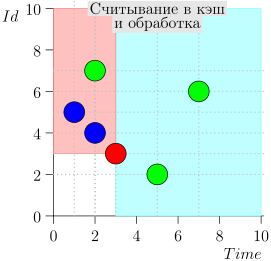
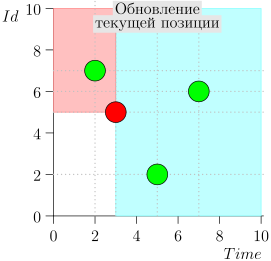
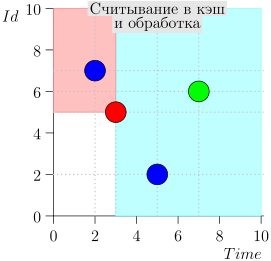
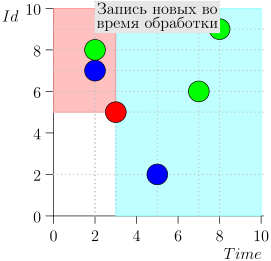
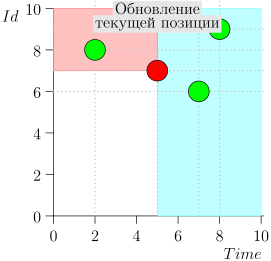
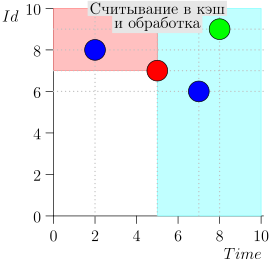
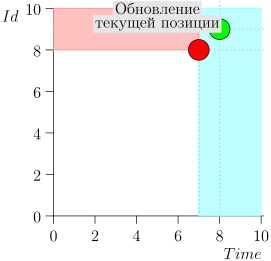
Resulta que el problema está resuelto? Pero no (Está claro que si el problema se resolvió por completo en esta etapa, entonces
este artículo no hubiera sido :))
El error?
De esta forma, el algoritmo funcionó durante bastante tiempo. Todas las pruebas salieron bien. Tampoco hubo problemas en la producción.
Pero el desarrollador del algoritmo y su implementación (mi colega Peter Reznikov) tiene mucha experiencia, e intuitivamente sintió que algo andaba mal aquí. Por lo tanto, se realizó un verificador junto al código principal, que se verificó de vez en cuando en un temporizador para ver si había algún evento perdido, y
si alguno, los procesé.
De esta forma, el sistema funcionó con éxito. Es cierto que nadie mantuvo estadísticas sobre el número de eventos seleccionados por el verificador. Entonces, desafortunadamente, no sabemos cuántas fallas se asociaron con el procesamiento de eventos inoportunos.
Implementé una cola similar de objetos con límite de tiempo. Al discutir la implementación y optimización de algoritmos con Peter Reznikov, hablamos sobre este algoritmo para trabajar con eventos. Dudaban de que el algoritmo sea correcto. Decidimos hacer un modelo pequeño para confirmar o disipar dudas. Como resultado, encontramos un error.
Modelo
Antes de desarmar la traza con un error, daré el código fuente del modelo en el que se detectó el error.
Las diferencias con el modelo anterior son muy pequeñas, solo hay un límite en el tamaño de los bloques de lectura: se agrega el operador Límite y, en consecuencia, se cambian los operadores de selección de eventos.
Para ahorrar espacio, dejé comentarios solo en las partes modificadas del modelo.
---------------- MODULE events ---------------- EXTENDS Naturals, FiniteSets, Sequences, TLC (* --algorithm Events \* LIMIT, \* \* \* variables Events = {}, Event_Id = 0, MAX_TIME = 5, LIMIT \in 1..3, TIME_DELTA \in 1..2 define ZERO_EVT == [time |-> 0, id |-> 0] MAX(S) == CHOOSE x \in S: \A y \in S: y <= x MIN(S) == CHOOSE x \in S: \A y \in S: y >= x RECURSIVE SetReduce(_, _, _) SetReduce(Op(_, _), S, value) == IF S = {} THEN value ELSE LET s == CHOOSE s \in S : TRUE IN SetReduce(Op, S \ {s}, Op(s, value)) ToSeq(S) == LET op(e, val) == Append(val, e) IN SetReduce(op, S, << >>) ToSet(S) == {S[i] : i \in DOMAIN(S)} MapSet(Op(_), S) == {Op(x) : x \in S} GetIds(Evts) == MapSet(LAMBDA x: x.id, Evts) GetTimes(Evts) == MapSet(LAMBDA x: x.time, Evts) EventsOrderByTime(e1, e2) == e1.time < e2.time EventsOrderById(e1, e2) == e1.id < e2.id EventsOrder(e1, e2) == \/ EventsOrderByTime(e1, e2) \/ /\ e1.time = e2.time /\ EventsOrderById(e1, e2) Limit(S, limit) == LET amount == MIN({limit, Len(S)}) result == IF amount > 0 THEN SubSeq(S, 1, amount) ELSE << >> IN result \* SELECT * FROM events \* WHERE time <= curr_time AND id > max_id \* ORDER BY id \* LIMIT limit SELECT_HIGH_PRIO(state, limit) == LET selected == {e \in Events : /\ e.time <= state.time /\ e.id >= state.id } \* Id sorted == SortSeq(ToSeq(selected), EventsOrderById) \* limited == Limit(sorted, limit) IN ToSet(limited) \* SELECT * FROM events \* WHERE time > current_time \* AND time - Time <= delta_time \* ORDER BY time, id \* LIMIT limit SELECT_NORMAL(state, delta_time, limit) == LET selected == {e \in Events: /\ e.time <= state.time + delta_time /\ e.time > state.time } \* sorted == SortSeq(ToSeq(selected), EventsOrder) \* limited == Limit(sorted, limit) IN ToSet(limited) ALL_EVENTS_PROCESSED(state) == \A e \in Events: \/ e.time >= state.time \/ e.id >= state.id end define; fair process inserter = "Sources" variable t; begin forever: while TRUE do get_time: with evt_time \in 0..MAX_TIME do t := evt_time; end with; commit: either Events := Events \union {[time |-> t, id |-> Event_Id]} || Event_Id := Event_Id + 1; or Event_Id := Event_Id + 1; end either; end while; end process fair process event_processor = "Event_processor" variable state = ZERO_EVT, events = {}; begin forever: while TRUE do select: events := LET evts_high_prio == SELECT_HIGH_PRIO(state, LIMIT) new_limit == LIMIT - Cardinality(evts_high_prio) evts_normal == SELECT_NORMAL(state, TIME_DELTA, new_limit) IN evts_high_prio \union evts_normal; proc_evts: Events := Events \ events || state := [ time |-> MAX({state.time} \union GetTimes(events)), id |-> MAX({state.id} \union GetIds(events))] || events := {}; end while; end process end algorithm; *) \* BEGIN TRANSLATION \* TLA+, PlusCal \* END TRANSLATION ===================================================
Un lector atento puede notar que, además de introducir Limit, las etiquetas en event_processor también se han cambiado. El objetivo es un poco mejor para simular el código real que dos selecciones ejecutan en una transacción, es decir, se puede decir que la selección de eventos se realiza atómicamente.
Bueno, y si encontramos un error en un modelo con operaciones atómicas más grandes, esto prácticamente garantiza que el mismo error ocurra en el mismo modelo, pero con pasos atómicos más pequeños (una declaración bastante fuerte, pero creo que es intuitivo; aunque debería ser bueno si no se prueba, luego se verifica en una amplia selección de modelos).
Verificación del modelo
Comenzamos la simulación con los mismos parámetros que en la primera realización.
Y obtenemos una violación de la propiedad ALL_EVENTS_PROCESSED en el paso 19 de la simulación al buscar en ancho.
Para los datos iniciales dados (este es un espacio de estado muy pequeño), el error en el paso 19 indica que el error es muy raro y difícil de detectar, ya que antes se examinaron todas las cadenas de estado con una longitud de menos de 19.
Por lo tanto, este error es difícil de detectar en las pruebas. Solo si sabe dónde buscar y específicamente selecciona pruebas y cabañas temporales.
No traeré toda la ruta por ahorrar espacio y tiempo. Aquí hay un segmento de varios estados junto con un error:
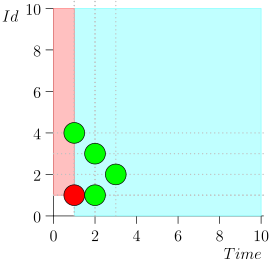

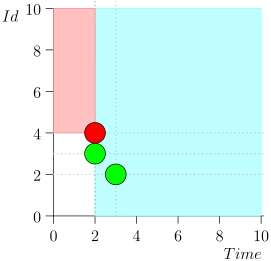
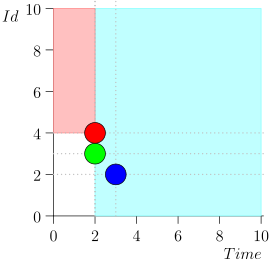
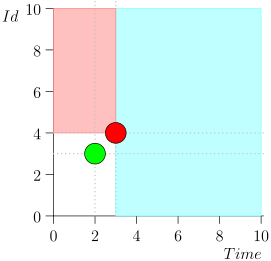
Análisis y corrección
Que paso
Como puede ver, el error se manifestó en el hecho de que perdimos el evento {2, 3} debido al hecho de que el límite terminó en el evento {2, 1}, y después de eso cambiamos el estado del coordinador. Esto puede suceder solo si en algún momento hay varios eventos.
Es por eso que el error fue esquivo en las pruebas. Para su manifestación, es necesario que coincidan cosas bastante raras:
- Varios eventos llegan al mismo punto en el tiempo.
- El límite en la selección de eventos finalizó antes del momento de leer todos estos eventos.
El error se puede corregir con relativa facilidad si el estado del coordinador se expande un poco: agregue el tiempo y el identificador del último evento de lectura desde el área de eventos normal con la identificación máxima si el tiempo de este evento corresponde al siguiente valor de estado.
Si no existe tal evento, establecemos el estado adicional (extra_state) en un estado no válido (UNDEF_EVT) y no lo tenemos en cuenta al trabajar.
Aquellos eventos de la región normal que no se procesaron en el paso anterior del coordinador, consideraremos que ya son de alta prioridad y, en consecuencia, corregiremos la selección de predicado de alta prioridad y seguridad.
Sería posible introducir otra área intermedia entre alta prioridad y normal, y cambiar el algoritmo. Primero, procesará los de alta prioridad, luego los intermedios, y luego pasará a los normales con el posterior cambio de estado.
Pero tales cambios conducirían a un mayor volumen de refactorización con beneficios obvios (el algoritmo será un poco más claro; otras ventajas no son visibles de inmediato).
Por lo tanto, decidimos ajustar solo ligeramente el estado actual y la selección de eventos de la base de datos.
Modelo ajustado
Aquí está el modelo corregido.
------------------- MODULE events ------------------- EXTENDS Naturals, FiniteSets, Sequences, TLC \* CONSTANTS MAX_TIME, LIMIT, TIME_DELTA (* --algorithm Events variables Events = {}, Limit \in LIMIT, Delta \in TIME_DELTA, Event_Id = 0 define \* \* , extra_state UNDEF_EVT == [time |-> MAX_TIME + 1, id |-> 0] ZERO_EVT == [time |-> 0, id |-> 0] MAX(S) == CHOOSE x \in S: \A y \in S: y <= x MIN(S) == CHOOSE x \in S: \A y \in S: y >= x RECURSIVE SetReduce(_, _, _) SetReduce(Op(_, _), S, value) == IF S = {} THEN value ELSE LET s == CHOOSE s \in S : TRUE IN SetReduce(Op, S \ {s}, Op(s, value)) ToSeq(S) == LET op(e, val) == Append(val, e) IN SetReduce(op, S, << >>) ToSet(S) == {S[i] : i \in DOMAIN(S)} MapSet(Op(_), S) == {Op(x) : x \in S} GetIds(Evts) == MapSet(LAMBDA x: x.id, Evts) GetTimes(Evts) == MapSet(LAMBDA x: x.time, Evts) EventsOrderByTime(e1, e2) == e1.time < e2.time EventsOrderById(e1, e2) == e1.id < e2.id EventsOrder(e1, e2) == \/ EventsOrderByTime(e1, e2) \/ /\ e1.time = e2.time /\ EventsOrderById(e1, e2) TakeN(S, limit) == LET amount == MIN({limit, Len(S)}) result == IF amount > 0 THEN SubSeq(S, 1, amount) ELSE << >> IN result (* SELECT * FROM events WHERE time <= curr_time AND id > max_id ORDER BY id Limit limit *) SELECT_HIGH_PRIO(state, limit, extra_state) == LET \* \* time <= curr_time \* AND id > maxt_id selected == {e \in Events : \/ /\ e.time <= state.time /\ e.id >= state.id \/ /\ e.time = extra_state.time /\ e.id > extra_state.id} sorted == \* SortSeq(ToSeq(selected), EventsOrderById) limited == TakeN(sorted, limit) IN ToSet(limited) SELECT_NORMAL(state, delta_time, limit) == LET selected == {e \in Events : /\ e.time <= state.time + delta_time /\ e.time > state.time } sorted == SortSeq(ToSeq(selected), EventsOrder) limited == TakeN(sorted, limit) IN ToSet(limited) \* extra_state UpdateExtraState(events, state, extra_state) == LET exact == {evt \in events : evt.time = state.time} IN IF exact # {} THEN CHOOSE evt \in exact : \A e \in exact: e.id <= evt.id ELSE UNDEF_EVT \* extra_state ALL_EVENTS_PROCESSED(state, extra_state) == \A e \in Events: \/ e.time >= state.time \/ e.id > state.id \/ /\ e.time = extra_state.time /\ e.id > extra_state.id end define; fair process inserter = "Sources" variable t; begin forever: while TRUE do get_time: with evt_time \in 0..MAX_TIME do t := evt_time; end with; commit: either Events := Events \union {[time |-> t, id |-> Event_Id]} || Event_Id := Event_Id + 1; or Event_Id := Event_Id + 1; end either; end while; end process fair process event_processor = "Event_processor" variable events = {}, state = ZERO_EVT, extra_state = UNDEF_EVT; begin forever: while TRUE do select: events := LET evts_high_prio == SELECT_HIGH_PRIO(state, Limit, extra_state) new_limit == Limit - Cardinality(evts_high_prio) evts_normal == SELECT_NORMAL(state, Delta, new_limit) IN evts_high_prio \union evts_normal; proc_evts: Events := Events \ events || state := [ time |-> MAX({state.time} \union GetTimes(events)), id |-> MAX({state.id} \union GetIds(events)) ]; extra_state := UpdateExtraState(events, state, extra_state) || events := {}; end while; end process end algorithm; *) \* BEGIN TRANSLATION \* TLA+, PlusCal \* END TRANSLATION ===================================================
Como puede ver, los cambios son muy pequeños:
- Se agregaron datos adicionales al estado extra_state.
- Cambió la selección de eventos de alta prioridad.
- UpdateExtraState extra_state.
- safety - .
, . , (, , , ).
, , TLA+/TLC . :)
Conclusión
, , ( , , , ).
, , TLA+/TLC, . , .
TLA+/TLC , , ( , ) .
, , , TLA+/TLC .
Libros
, , , . .
Michael Jackson Problem Frames: Analysing & Structuring Software Development Problems
( !), . , . , .
Hillel Wayne Practical TLA+: Planning Driven Development
TLA+/PlusCal . , . . : .
MODEL CHECKING.
. , , . , .
Leslie Lamport Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers
TLA+. , . : , . , TLA+ , .
Formal Development of a Network-Centric RTOS
TLA+ ( RTOS ) TLC.
, . , TLA+ , , RTOS — Virtuoso. , .
, (, , , , ).
w Amazon Web Services Uses Formal Methods
TLA+ AWS. : http://lamport.azurewebsites.net/tla/amazon-excerpt.html
Hillel Wayne ( "Practical TLA+")
. , . , - .
Ron Pressler
. . , TLA+. TLA+, computer science .
Leslie Lamport
TLA+ computer science . TLA+ .
. . , . . , . . .
, , .
TLA+,
, TLA+. , TLA+.
Hillel Wayne
Hillel Wayne . .
Ron Pressler
, Hillel Wayne, . , . Ron Pressler . ́ , , .
TLA toolbox + TLAPS : TLA+
. Alloy Analyzer .