Hola a todos! Mi nombre es Dmitry Rudnev, soy desarrollador frontend en BCS. Comencé mi viaje con el diseño de interfaces de diversa complejidad y siempre presté especial atención a la interfaz: qué tan cómodo sería para el usuario interactuar con él, si pudiera transmitirle al usuario la interfaz tal como la diseñó el diseñador.
En esta serie de artículos quiero compartir mi experiencia en la aplicación de prácticas funcionales en el desarrollo frontend, hablaré sobre los pros y los contras que recibirá como desarrollador al usar estas prácticas. Si le gusta el tema, nos sumergiremos en los rincones más "secos" y más complejos del mundo funcional. Noto de inmediato que pasaremos de mayor a menor, es decir, veremos la aplicación clásica desde una vista de pájaro y, a medida que avancemos en los artículos, bajaremos a donde la práctica específica nos traerá beneficios notables.
Entonces, comencemos manejando los estados. Al mismo tiempo te lo diré, y aquí, en general, mónadas y funcionistas.
Introducción
Al desentrañar la siguiente interfaz y encontrar puntos en común entre la interfaz de usuario y el análisis, comencé a notar que cada vez que un desarrollador trata con una red, solo necesita procesar todos los estados de la interfaz de usuario y describir la reacción a un estado en particular. Y dado que cada uno de nosotros lucha por la excelencia, existe el deseo de que esta forma de procesar estados muestre un patrón que describa de la manera más transparente posible lo que está sucediendo y cuál es el iniciador de una reacción particular y, como resultado, el resultado del trabajo. Afortunadamente, en el mundo de la programación, casi todo lo que se te ocurre fue implementado por alguien antes que tú.
Tanto en el mundo del desarrollo como en el mundo del diseño, no solo se formaron patrones que le permiten resolver eficazmente sus problemas, sino también antipatters, que deben evitarse por todos los medios para que las malas prácticas no prosperen, y el desarrollador o diseñador siempre tuvo un punto de apoyo en las situaciones, cuando no hay una solución concreta
En nuestro caso, la situación que tienen la mayoría de los desarrolladores es el procesamiento de todos los estados del elemento UI y la reacción a ellos. El problema aquí es que el elemento UI puede interactuar tanto con el estado local (sin ejecutar solicitudes asincrónicas) como con recursos o repositorios remotos. Los desarrolladores a veces se olvidan de manejar todos los casos extremos, lo que conduce a un comportamiento inconsistente del sistema en su conjunto.
Todos los ejemplos contendrán ejemplos de código utilizando la biblioteca React y un superconjunto de JavaScript - TypeScript, así como bibliotecas para la programación funcional de fp-ts.
Considere el ejemplo más simple, donde tenemos una lista de elementos que solicitamos del servidor, y necesitamos mostrar correctamente la IU de acuerdo con el resultado de la solicitud. Estamos interesados en la función de
render , porque en ella necesitamos mostrar el estado correcto durante la ejecución de la solicitud. El código de ejemplo completo se puede ver en:
aplicación simple . En el futuro, habrá disponible un proyecto completo, centrado en una serie de artículos, donde en el curso desmontaremos sus partes individuales.
const renderInitial = (...) => ...; const renderPending = (...) => ...; const renderError = (...) => ... ; const renderSuccess = (...) => ... ; return ( {state.subcribers.foldL( renderInitial, renderPending, renderError, renderSuccess, )} );
El ejemplo muestra claramente que cada estado del modelo de datos tiene su propia función, y cada función devuelve un fragmento de la IU prescrita (mensaje, botón, etc.). Mirando hacia el futuro, diré que el ejemplo usa
RemoteData monad .
Es tan elegante y, lo más importante, seguro, podemos trabajar con datos y responder a ellos. Esta fue la introducción, donde intenté demostrar los beneficios de un enfoque funcional en un ejemplo tan aparentemente simple.
Functor y mónada
Ahora, comencemos a sumergirnos gradualmente en la teoría aplicada de categorías y analizar conceptos como
Functor y
Monad , y también consideremos prácticas para trabajar con datos de manera segura utilizando prácticas funcionales.
“Esencialmente, un functor no es más que una estructura de datos que le permite aplicar funciones de transformación para extraer valores de un shell, modificarlos y luego volver a colocarlos en el shell.
El encerrar valores en un shell o contenedor es un patrón de diseño fundamental en la programación funcional, ya que protege contra el acceso directo a los valores, lo que les permite ser manipulados de forma segura y sin cambios en los programas de aplicación ".Tomé esta cita de un
libro maravilloso
sobre la revisión de técnicas de programación funcional en JavaScript . Comencemos con el componente teórico y analicemos qué es realmente un functor. Para empezar, necesitamos familiarizarnos con una sección fascinante de las matemáticas llamada teoría de categorías en el nivel más básico.
La teoría de categorías es una rama de las matemáticas que estudia las propiedades de las relaciones entre los objetos matemáticos, independientemente de la estructura interna de los objetos. La teoría de categorías ocupa un lugar central en las matemáticas modernas; también ha encontrado aplicaciones en informática, lógica y física teórica.Una categoría consta de objetos y flechas que se dirigen entre ellos. La forma más fácil de visualizar una categoría es:
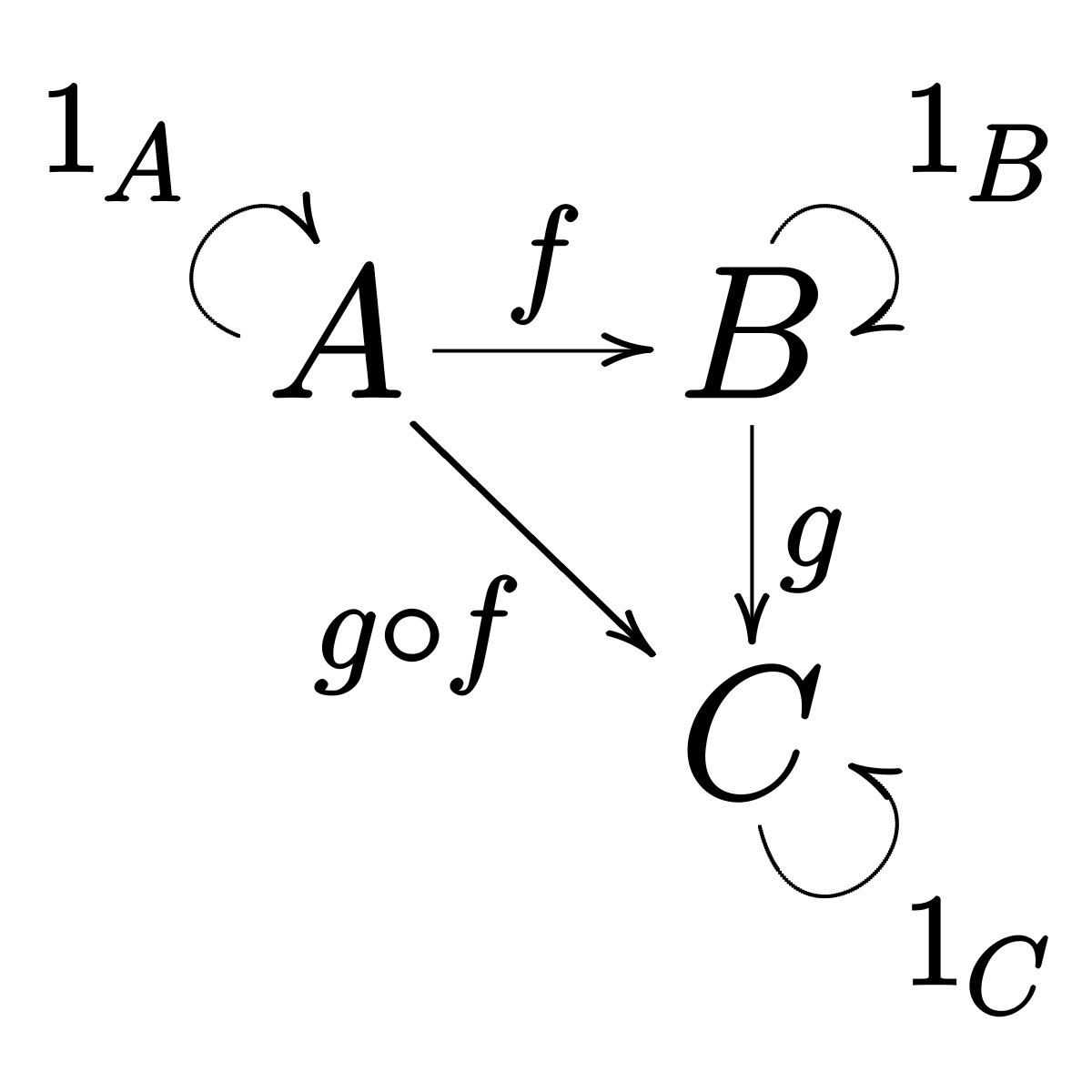
Las flechas están dispuestas de manera que si tiene una flecha del objeto
A al objeto
B y una flecha del objeto
B a
C , entonces debe haber una flecha: su composición es de
A a
C. Piense en las flechas como funciones; También se les llama morfismos. Tiene una función
f que toma A como argumento y devuelve B. Hay otra función
g que toma B como argumento y devuelve C. Puede combinarlos pasando el resultado de
f a
g . Acabamos de describir una nueva función que toma A y devuelve C. En matemáticas, dicha composición se denota mediante un pequeño círculo entre la notación de función: g ◦ f. Presta atención al orden de composición, de derecha a izquierda.
En matemáticas, la composición se dirige de derecha a izquierda. En este caso, ayuda si lee g ◦ f como “g después de f”.
-— A B f :: A -> B -— B g :: B -> C -— A C g . f
Hay dos propiedades muy importantes que una composición debe satisfacer en cualquier categoría.
- La composición es asociativa (la asociatividad es una propiedad de las operaciones que le permite restaurar la secuencia de su ejecución en ausencia de indicaciones explícitas de sucesión con igual prioridad; esto distingue entre la asociatividad izquierda, donde la expresión se evalúa de izquierda a derecha, y la asociatividad derecha de derecha a izquierda. Los operadores correspondientes se denominan asociativo izquierdo y asociativo derecho Si tiene tres morfismos (flechas), f, gyh, que se pueden organizar (es decir, sus tipos son consistentes entre sí), usted necesita paréntesis, a agruparlos. Matemáticamente, esto se escribe como
h ◦ (g ◦ f) = (h ◦ g) ◦ f = h ◦ g ◦ f (h ◦ g) ◦ f = h ◦ g ◦ f - Para cada objeto A hay una flecha, que será una unidad de composición. Esta flecha es de un objeto a sí misma. Ser una unidad de composición significa que al componer una unidad con cualquier flecha que comience en A o termine en A, respectivamente, la composición devuelve la misma flecha. La flecha de la unidad de un objeto A se llama IDa (unidad en A). En notación matemática, si f va de A a B, entonces
f ◦ idA = f
Para trabajar con funciones, se implementa una sola flecha como una función idéntica, que simplemente devuelve su argumento.
Ahora podemos considerar qué es un functor en la teoría de categorías.
Un functor es un tipo especial de mapeo entre categorías. Se puede entender como una pantalla que conserva la estructura. Los functores entre categorías pequeñas son morfismos en la categoría de categorías pequeñas. La totalidad de todas las categorías no es una categoría en el sentido habitual, ya que la totalidad de sus objetos no es una clase. -
Wikipedia .
Considere un ejemplo de la implementación de un functor para el contenedor Maybe, que es la idea de un "valor que puede estar ausente".
const compose = <A, B, C>( f: (a: A) => B, g: (b: B) => C, ): (a: A) => C => (a: A) => g(f(a)); // Maybe: type Nothing = Readonly<{ tag: 'Nothing' }>; type Just<A> = Readonly<{ tag: 'Just'; value: A }>; export type Maybe<A> = Nothing | Just<A>; const nothing: Nothing = { tag: 'Nothing' }; const just = <A>(value: A): Just<A> => ({ tag: 'Just', value }); // Maybe: const fmap = <A, B>(f: (a: A) => B) => (fa: Maybe<A>): Maybe<B> => { switch (fa.tag) { case 'Nothing': return nothing; case 'Just': return just(f(fa.value)); } }; // 1: fmap id === id namespace Laws { console.log( fmap(id)(just(42)), id(just(42)), ); // => { tag: 'Just', value: 42 } // 2: fmap f ◦ fmap g === fmap (f ◦ g) const f = (a: number): string => `Got ${a}!`; const g = (s: string): number => s.length; console.log( compose(fmap(f), fmap(g))(just(42)), fmap(compose(f, g))(just(42)), ); // => { tag: 'Just', value: 7 } }
El método
fmap se puede ver desde dos lados:
- Como una forma de aplicar una función pura a un valor "contenedorizado";
- Como una forma de "elevar al contexto contenedor" una función pura.
De hecho, si los corchetes en la interfaz son ligeramente diferentes, podemos obtener la firma de la función
fmap :
const fmap: <A, B>(f: (a: A) => B) => ((ma: Maybe<A>) => Maybe<B>);
Habiendo definido la interfaz:
type Function1<Domain, Codomain> = (a: Domain) => Codomain;
obtenemos la definición de
fmap :
const fmap: <A, B>(f: (a: A) => B) => Function1<Maybe<A>, Maybe<B>>;
Este simple truco nos permite pensar en un functor como una forma de "elevar una función pura a un contexto contenedor". Gracias a esto, es posible trabajar con varios tipos de datos de manera segura: por ejemplo, procesar con éxito cadenas de valores anidados opcionales; Convertir listas de datos manejar excepciones y más.
Como se explicó anteriormente, utilizando los functores, puede aplicar funciones a valores de forma segura e inmutable. Las mónadas son similares a los functores, excepto que pueden delegar lógica especial en casos especiales. El propio functor solo sabe cómo aplicar esta función y envolver el resultado en un shell, y no tiene lógica adicional.
Una mónada surge cuando se crea un tipo de datos completo por el principio de extraer datos por el principio de extraer valores de shells y definir reglas de anidamiento. Al igual que los functores, las mónadas son una plantilla de diseño utilizada para describir los cálculos en forma de una secuencia de etapas donde el valor procesado no se conoce en absoluto, pero son las mónadas las que permiten controlar de forma segura y sin efectos secundarios el flujo de datos cuando se usan en la composición. Las mónadas pueden estar dirigidas a resolver una variedad de problemas. Teóricamente, las mónadas dependen del sistema de tipos en un idioma en particular. De hecho, muchas personas piensan que solo pueden entenderse si hay tipos de datos explícitos.
Para comprender mejor las mónadas, se deben aprender los siguientes conceptos importantes.
Mónada Proporciona una interfaz abstracta para operaciones monádicas.
Tipo monádico. Implementación específica de esta interfaz
Pero ejemplos prácticos de la aplicación de estas propiedades de un functor y otras construcciones categóricas que mostraré en futuros artículos.