Sobre coordenadas barcéntricas en los dedos

Hola

Seguramente todo el mundo ha sido testigo de una evaluación mirilla del grado de similitud del niño con los padres: algo así como "se derramó papá, ¡pero él también se parece a mamá!"


( tomado de aquí )

Como en el ejemplo de la imagen, puede evaluar el grado de similitud en porcentaje. También puede usar parientes para describir con mayor precisión la cara del bebé en forma de una suma ponderada de parientes de parientes ...

Y se verá y se percibirá de forma bastante natural para una persona "ordinaria" que no está asociada con la antropología o, por ejemplo, la ciencia forense. Para un profesional en el campo del análisis y el reconocimiento de rostros, es más probable que un rostro humano sea un conjunto de parámetros. Es decir, un punto (un conjunto de coordenadas) en algún espacio con una base (ejes correspondientes a los parámetros). Y si describimos la cara del niño en comparación con sus parientes, lo más probable es que el punto correspondiente a la cara del niño aparezca en este espacio de parámetros dentro del casco convexo de la nube de puntos correspondientes a las caras de los familiares (pero esto no es exacto).

En realidad, de qué se trata ... Estos dos enfoques para la descripción de caras corresponden a dos sistemas de coordenadas:

1. baricéntrico, descripción de un punto en el espacio (en nuestro ejemplo: cara) a través de una mezcla ponderada de otros puntos;
2. afín, una descripción de un punto en el espacio a través de coordenadas en alguna base.

Entonces, ¿qué son las coordenadas barcéntricas?

Dejar entrar -dimensional espacio dado punto con vectores de radio , . Además, ninguno de los puntos se encuentra en la capa lineal de los vectores de radio de los puntos restantes ... En pocas palabras, es bastante simple: deje que estos puntos formen una figura que no se pueda representar completamente en un espacio con una dimensión inferior a .

En el caso del espacio unidimensional (línea), necesitamos 2 puntos no coincidentes, en el caso del espacio bidimensional, un triángulo no degenerado, en el caso tridimensional, un tetraedro.

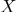
Entonces cualquier punto en el espacio puede ser representado por un vector de radio :



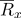
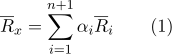
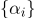
Set y hay coordenadas barcéntricas.

¿Cómo son las coordenadas barcéntricas mejores / peores que afines?

Comencemos con las desventajas relativas:

1. en la representación barcéntrica, necesitamos una coordenada más que en la afín;
2. La distancia entre puntos especificados barcéntricamente no se puede calcular directamente en estas coordenadas.

En parte, el primer inconveniente se compensa con el hecho de que a pesar de la necesidad de usar coordenadas barcéntricas al describir un punto en -Espacio dimensional, el número de grados no aumenta. Las coordenadas barcéntricas definidas en la fórmula (1) están relacionadas por la relación:



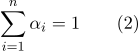
En cuanto al segundo inconveniente, si es necesario calcular la distancia entre puntos representados barcéntricamente, entonces tiene sentido calcular productos escalares y usa el análogo de la distancia de Mahalanobis.

¿Cuáles son los bonos por usar coordenadas barcéntricas?

1. Las coordenadas barcéntricas son invariantes para las transformaciones afines del espacio. Esta propiedad se usa, por ejemplo, para la interpolación lineal en gráficos de computadora. Deje que las coordenadas de textura se definan en los vértices de un elemento de superficie triangular 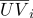y normales ( 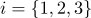), cada punto de esta sección de superficie tendrá coordenadas barcéntricas 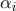sus coordenadas de textura 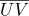y normal 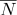se puede calcular como:
   
   
   
   
   
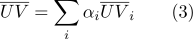
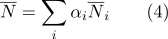
2. Por coordenadas barcéntricas es fácil determinar si un punto pertenece 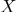partes del espacio delimitadas por un poliedro con vértices : esto solo se hace si . La igualdad de la coordenada barcéntrica i-ésima 1 significa que el punto coincide con . Si varias coordenadas barcéntricas son iguales a 0, esto significa que el punto pertenece a un subespacio atravesado por los vectores de radio de los puntos restantes cuyas coordenadas correspondientes son mayores que 0.

¿Quizás son muy difíciles de calcular?

No más complicado que cualquier transformación lineal del sistema de coordenadas. Porque, en esencia, el cálculo de las coordenadas barcéntricas es una transformación.

Reescribimos el vector radio de puntos en la siguiente forma:

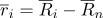
donde - un vector radial en el sistema de coordenadas centrado en un punto .

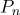
Entonces la fórmula (1) puede reescribirse en la siguiente forma:



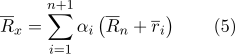
Revelaremos los corchetes en la suma:



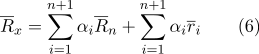
Según la propiedad (2):



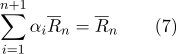
En consecuencia:

,

donde

Dado (2), nos limitamos a calcular las primeras n coordenadas barcéntricas. Imagine la transición a coordenadas barcéntricas como una transformación lineal:

,

donde - vector n de coordenadas barcéntricas (excepto la última), - matriz de transformación.

Dadas las propiedades de la representación barcéntrica, si como sustituir uno de los vectores ( ), obtenemos un vector con cero componentes, excepto uno i-ésimo, que será igual a 1.

Si la matriz multiplicar por matriz compuesto por columnas de , entonces deberíamos obtener la matriz de identidad (una matriz con unos en la diagonal principal y ceros en los elementos restantes):

,

donde , Es la matriz de identidad ( - Símbolo de Kronecker: 1 si de lo contrario 0).

De (10) encontramos :



Por lo tanto, tener un conjunto de puntos con vectores de radio , Podemos calcular la matriz para convertir a coordenadas barcéntricas:



Usando esta matriz, podemos obtener el primer coordenadas de punto baricéntrico con vector de radio :



Usando la relación (2) nuevamente, obtenemos la última coordenada barcéntrica:

Conclusión

Quizás a primera vista, el barcéntrico también parece incómodo y complejo. Pero, de hecho, esta es una herramienta muy conveniente e indispensable en muchas tareas, a las que te acostumbras rápidamente. ¡Porque no hay magia aquí, es álgebra lineal en su forma más pura!