Regresión lineal y descenso de gradiente

Deje que los indicadores X e Y, que tienen una expresión cuantitativa, se estudien en un área temática determinada.

Además, hay muchas razones para creer que el indicador Y depende del indicador X. Esta posición puede ser tanto una hipótesis científica como estar basada en el sentido común elemental. Por ejemplo, tome tiendas de abarrotes.

Denote por:

X - área de ventas (sq. M.)

Y - volumen de negocios anual (millones p.)

Obviamente, cuanto mayor sea el área de negociación, mayor será el volumen de negocios anual (asumimos una relación lineal).

Imagine que tenemos datos sobre algunas n tiendas (espacio comercial y facturación anual), nuestro conjunto de datos yk espacio comercial (X), para las cuales queremos predecir la facturación anual (Y), nuestra tarea.

Presumimos que nuestro valor de Y depende de X en la forma: Y = a + b * X

Para resolver nuestro problema, debemos elegir los coeficientes a y b.

Primero, establezcamos valores aleatorios ayb. Después de eso, necesitamos determinar la función de pérdida y el algoritmo de optimización.

Para hacer esto, podemos usar la función de pérdida cuadrática media raíz ( MSELoss ). Se calcula mediante la fórmula:



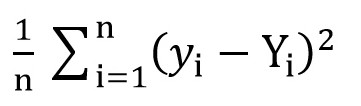
Donde y [i] = a + b * x [i] después de a = rand () y b = rand (), e Y [i] es el valor correcto para x [i].
En esta etapa, tenemos la desviación estándar (una cierta función de ayb). Y es obvio que, cuanto menor es el valor de esta función, más precisamente se seleccionan los parámetros ayb con respecto a aquellos parámetros que describen la relación exacta entre el área del espacio comercial y el volumen de negocios en esta sala.

Ahora podemos comenzar a usar el descenso de gradiente (solo para minimizar la función de pérdida).

Descenso de gradiente

Su esencia es muy simple. Por ejemplo, tenemos una función:

y = x*x + 4 * x + 3 

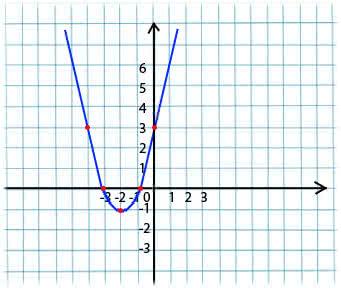
Tomamos un valor arbitrario de x del dominio de definición de la función. Imagine que este es el punto x1 = -4.

Luego, tomamos la derivada con respecto a x de esta función en el punto x1 (si la función depende de varias variables (por ejemplo, ayb), entonces necesitamos tomar las derivadas parciales para cada una de las variables). y '(x1) = -4 <0

Ahora obtenemos un nuevo valor para x: x2 = x1 - lr * y '(x1). El parámetro lr (tasa de aprendizaje) le permite establecer el tamaño del paso. Así obtenemos:

Si la derivada parcial en un punto dado x1 <0 (la función disminuye), entonces nos movemos al punto de mínimo local. (x2 será mayor que x1)

Si la derivada parcial en un punto dado x1> 0 (la función aumenta), entonces todavía nos estamos moviendo al punto de mínimo local. (x2 será menor que x1)

Al realizar este algoritmo de forma iterativa, nos acercaremos al mínimo (pero no lo alcanzaremos).

En la práctica, todo esto parece mucho más simple (sin embargo, no presumo decir qué coeficientes ayb se ajustarán con mayor precisión con el caso anterior con las tiendas, por lo que tomamos una dependencia de la forma y = 1 + 2 * x para generar el conjunto de datos, y luego entrenamos nuestro modelo en este conjunto de datos):
(El código está escrito aquí )

 import numpy as np #      np.random.seed(42) #  np-  1000     0..1 sz = 1000 x = np.random.rand(sz, 1) #   y = f(x)      y = 1 + 2 * x + 0.1 * np.random.randn(sz, 1) #    0  999 idx = np.arange(sz) #    np.random.shuffle(idx) train_idx = idx #     x_train, y_train = x[train_idx], y[train_idx] #        a = np.random.randn(1) b = np.random.randn(1) print(a,b) #   lr = 0.01 #   n_epochs = 10000 #   for epoch in range(n_epochs): #       a  b #     yhat = a + b * x_train # 1.   #      : error = (y_train - yhat) # 2.   (  ) #   a a_grad = -2 * error.mean() #   b b_grad = -2 * (x_train * error).mean() # 3.  ,     a = a - lr * a_grad b = b - lr * b_grad print(a,b) 

Una vez compilado el código, puede ver que los valores iniciales de a y b estaban lejos del 1 y 2 requeridos, respectivamente, y los valores finales están muy cerca.

Aclararé un poco de por qué a_grad y b_grad se consideran de esa manera.
F(a, b) = (y_train - yhat) ^ 2 = (1 + 2 * x_train – a + b * x_train) . La derivada parcial de F con respecto a a será -2 * (1 + 2 * x_train – a + b * x_train) = -2 * error . La derivada parcial de F con respecto a b será -2 * x_train * (1 + 2 * x_train – a + b * x_train) = -2 * x_train * error . Tomamos el valor medio (mean()) ya que error y x_train e y_train son matrices de valores, ayb son escalares.

Materiales utilizados en el artículo:

intodatascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html