🔡 😖 🌘 El número subyacente de la música moderna. 🕗 🅰️ 🚴

¿Por qué doce?

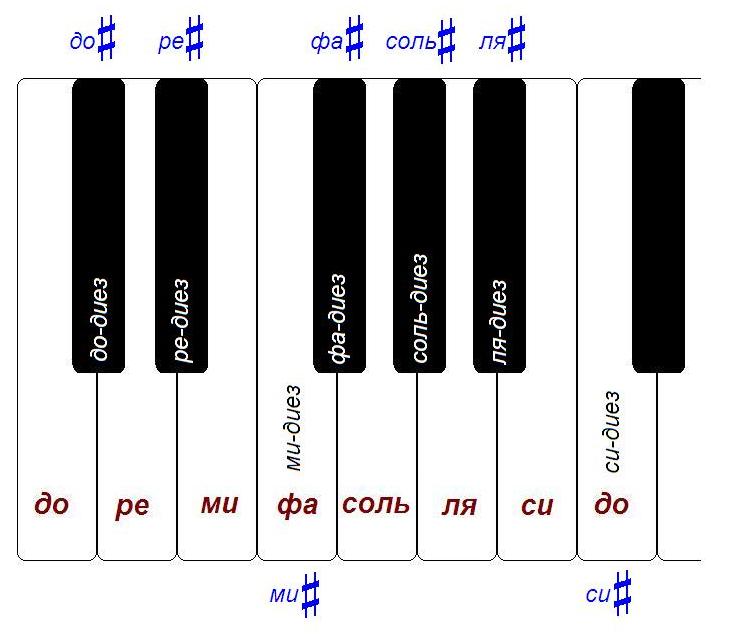
Si observa el teclado, verá que cada octava contiene 12 semitonos.
En el caso del piano, esto solo significa que, por ejemplo, entre "a" la primera octava y "a" la segunda octava, hay 11 teclas. Junto con uno de los "do" (por ejemplo, hasta la segunda octava) obtenemos 12 teclas: do #, re, re #, mi, fa, fa #, salt, salt #, la, la #, si, do.

¿Pero por qué 12?

Tal vez esto es solo un accidente? A nuestros antepasados les gustó el número 12, tienen 12 en todas partes: 12 meses, 12 signos del zodíaco, 12 tribus de Israel, 12 apóstoles, ... y aquí decidieron, que sea 12, y así se ordenó. ¿O todavía hay una ley objetiva, y este número no es accidental?

En este artículo intentaré demostrar que esto no es un accidente. Los requisitos suficientemente generales, bastante naturales para la música moderna (occidental), con necesidad matemática, nos llevan al número 12. Es interesante que la razón por la que tenemos este valor sea la propiedad de otro número (ver el final del artículo). Incluso puede decir que se encuentra en el corazón del sonido moderno.

Declaración del problema.

Primero, intentemos formalizar la tarea.

Tenemos una frecuencia de referencia $\ omega_0$ . Lo llamaremos tónico. También tenemos una octava con una frecuencia. $2 \ omega_0$ . Ahora necesitamos entender qué opciones para frecuencias intermedias de $\ omega_0$ antes $2 \ omega_0$ , de modo que una melodía construida sobre estas notas sonaría armoniosa para nuestros oídos?

Me temo que esta formulación, aunque refleja la esencia de la pregunta, sigue siendo, desde un punto de vista matemático, bastante vaga, y esa pregunta no se puede responder de manera inequívoca, solo porque el oído humano tiene una resolución de frecuencia bastante limitada. Y esto se confirma por el hecho de que en diferentes momentos se usaron diferentes melodías, por ejemplo, Pitágoras , melodías limpias , bien templadas y templadas uniformemente . Y todos sonaron y sonaron, al menos para ciertas obras, bastante aceptables.

¿Qué es la armonía?

Debemos imponer algunas condiciones adicionales. Pero primero, debemos responder una pregunta importante: ¿qué percibimos como sonido armonioso?

Veamos dos sonidos, con frecuencias $\ omega_1$ y $\ omega_2$ .

Toma la relación de estas frecuencias. Esta relación se puede representar como un producto de números. $a_1 ^ {k_1} \ cdot a_2 ^ {k_2} \ cdot ... \ cdot a_l ^ {k_l}$ donde $inline$ Son números primos y $inline$ - enteros, por ejemplo, esta relación puede ser igual $2 ^ {- 3} \ cdot3 \ cdot5$ . Y que estos números primos ( $inline$ ) menos, más armonioso para nuestro oído sonará este intervalo (encontré esta declaración aquí (ver el segundo párrafo) )

Entonces, por ejemplo, el sonido más armonioso de acuerdo con esta declaración será una octava (cambio de frecuencia de 2 veces). Y los próximos intervalos armónicos serán el quinto (cambio de frecuencia en $inline$ veces) y un cuarto (cambio de frecuencia en $inline$ tiempos).

Pero no es tan simple con esta afirmación. Entonces, por ejemplo, no está muy claro cómo afecta el grado. Por ejemplo, ¿qué es la multiplicación más armoniosa por $inline$ o 7? No sé si esta pregunta ha sido estudiada o no, y es posible, en principio, responderla. Además, la percepción de la armonía es algo bastante subjetivo. Entonces, la música moderna está llena de sonidos que habrían sido percibidos como una terrible cacofonía durante 100-200 años.

La primera condición. Tónico, Cuarto, Quint, Octava

Esta incertidumbre no es un problema para nuestra pequeña investigación. El hecho es que la única conclusión que quiero sacar de esta declaración es que en nuestro caso, en cualquier caso, debería haber al menos los intervalos "más armoniosos", a saber, una octava, un cuarto y un quinto. Es decir, junto con tónico con una frecuencia $\ omega_0$ y octava con una frecuencia $2 \ omega_0$ también debemos tener un quinto y un cuarto, con frecuencias respectivamente ${3 \ sobre 2} \ omega_0$ , ${4 \ sobre 3} \ omega_0$ o algo muy cercano que no pudimos distinguir de un quinto y un cuarto puros.

Nota: de hecho, solo tónicos, quintos y octavas son suficientes. La presencia de un quinto nos está dando inmediatamente un cuarto, como una adición a una octava, y en virtud de la segunda condición (invariancia), que se describe a continuación, también debemos tener un cuarto y un tónico. Es decir, la necesidad de un cuarto de galón es consecuencia de la presencia de un quinto y el requisito de invariancia.

Y este es nuestro primer requisito.

La segunda condición. Invariancia

Nuestro segundo requisito es la invariancia. Y este es un requisito importante de la música moderna. Este requisito consiste en el hecho de que todas las armonías en cualquier tecla deben sonar igual. Si hablamos del sistema moderno, que se usa para afinar el piano, esto significa que el quinto, que consta de siete medios tonos, debería sonar igual, independientemente del sonido del que esté construido. Es decir, la relación de frecuencia entre do y salt debe ser la misma que para do # - salt #, re - la, re # - la #, ... e igual $inline$ . Y esta invariancia debería aplicarse, por supuesto, no solo al quinto, sino también a cualquier intervalo. Una ventaja importante de este sistema es la capacidad de transponer la jugada en cualquier intervalo. Esta es la esencia del temperamento uniforme.

Debo decir que este requisito de invariancia no es tan obvio, y este enfoque se aplicó relativamente recientemente, solo en el siglo XVIII. Los sistemas utilizados antes (por ejemplo, Pitágoras y puro) no poseían dicha propiedad. Por ejemplo, escuche Sonata para Microtonal Piano (Ben Johnston) , escrito en un sistema limpio (límite máximo = 5). Parece que el piano no está afinado. Toda la riqueza de las armonías modernas se basa precisamente en esta invariancia. Por ejemplo, el "Clavier bien templado" de Bach apareció precisamente gracias a un nuevo enfoque para afinar teclados. Fue esta invariancia la que permitió a Bach crear secuencias armónicas que antes eran simplemente imposibles.

Entonces, ahora tenemos todos los datos necesarios para el cálculo.

Calculo

Construyamos una escala de tónicos a octavas que satisfaga ambos requisitos.
Supongamos que en este caso obtenemos $inline$ sonidos (incluida una octava). Es $inline$ y es el número deseado. Queremos mostrar que $inline$ bajo nuestras condiciones debe ser 12.

Una consecuencia del segundo requisito es que el intervalo entre las frecuencias de los sonidos vecinos debe ser igual e igual. $2 ^ {1 \ sobre N}$ .

Ahora, el primer requisito dice que en nuestra fila debe haber dos sonidos correspondientes a las frecuencias (con una buena aproximación) ${3 \ sobre 2} \ omega_0$ y ${4 \ over3} \ omega_0$ . Este es el quinto y cuarto. Supongamos que un cuarto es $inline$ suena en nuestra fila, y el quinto - $inline$ oh Denotamos $inline$ .

Es fácil ver que el cambio de frecuencia entre el cuarto y el quinto (relación de frecuencia) es $inline$ .

Pero, de acuerdo con nuestra segunda condición, esto también debería ser igual $2 ^ {n \ sobre N}$ .

Entonces tenemos la fórmula:

$2 ^ {n \ over N} \ aprox 9/8$

Después de transformaciones simples, obtenemos la fórmula básica:

$n \ aprox. N (2 \ log_2 {3} - 3) = N \ cdot 0.170$

Es fácil ver que la solución (por supuesto, aproximada) es $inline$ donde $inline$ - cualquier número naturalmente (lo suficientemente pequeño, porque, sin embargo, 0.170 difiere de 1/6).

Veamos un caso $inline$ . En este caso $inline$ , $inline$ . Es decir, esta es una variante del sistema moderno, solo sin medios tonos, solo con tonos (do, re, mi, fa #, salt #, la #, do). Pero, como puede ver, en este caso el cuarto (f) y el quint (sal) no cayeron en esta escala.

Es decir, la única opción para nosotros puede ser

$inline$ donde $inline$ - cualquier número natural ( $inline$ lo suficientemente pequeño). Caso $inline$ simplemente corresponde a nuestro sistema moderno, que se llama sistema uniformemente temperamental.

¿Pero por qué no 24 o más? La razón es simple: puedo suponer que tal graduación ya es excesiva para nuestra percepción. Por lo tanto, solo queda un número: 12.

Si no está satisfecho con el tren de pensamiento dado, aquí puede encontrar

prueba matemática rigurosa

Desafío:

Encuentre el número entero mínimo positivo N en el que hay un número entero positivo $inline$ tal que $2 ^ {n \ sobre N}$ diferente de $3 \ over2$ no más que $\ delta$ centavos

Solución:

Denote por $Z_n = N \ cdot (log_2 {3} -1)$ . Entonces, con $\ delta <{1200 \ sobre N}$ (lo cual es cierto para el rango de esos $\ delta$ y $inline$ que consideraremos) nuestra tarea es encontrar el mínimo $inline$ en que

${1200 \ over N} \ cdot | Z_n - redondo (Z_n) | <\ delta$ ,

donde $inline$ - redondeo de función al entero más cercano.

Resolveremos este problema numéricamente.

imagen

Ahora es tiempo de decidir $\ delta$ .

¿Qué cantidad (en centavos) de la discrepancia entre el quinto puro y "nuestro quinto" consideramos aceptable? Mucha gente escucha, por ejemplo, que el tercio grande / pequeño en el sistema de temperatura uniforme "falsifica". Pero esto es solo alrededor de 15 centavos en relación con los intervalos puros. Por lo tanto, nuestro requisito debe ser mejor que 15 centavos. Algunas fuentes dicen que a ciertas frecuencias, los músicos distinguen hasta 5 - 6 centavos. Por lo tanto sabio tomar $\ delta = 5$ .

Entonces la tabla muestra claramente que el más pequeño $inline$ . Los siguientes son satisfactorios $inline$ .

Nota:
Próxima iteración, para cada $inline$ También debe verificar el sonido y otros intervalos. En caso de $inline$ por ejemplo, los tercios se vuelven completamente "falsos": más de 30 centavos (para un tercio grande).

Entonces nuestra respuesta es: $inline$ . Lo cual se requería para probar.

Y, por cierto, está claro que nuestra respuesta no cambiará si en su lugar $\ delta = 5$ tomar, por ejemplo, 10 o incluso 15.

Conclusión Número subyacente

Sorprendentemente, resulta que el número que subyace en el sistema musical moderno y la música contemporánea (europea) es $\ log_2 {3}$ , a saber, que con buena precisión (0.1%) se cumple la siguiente igualdad:

$\ log_2 {3} \ aprox 19/12$

Respuestas a comentarios y críticas en los comentarios.

En primer lugar, ¡gracias por los interesantes comentarios!
Aquí están mis respuestas a los comentarios y críticas más importantes (en mi opinión).

Crítica 1. Huevo o pollo

Druu: Mira, 12 sonidos en una octava fue hasta un temperamento uniforme en general, por lo que no puedes justificar 12 sonidos con la ayuda del temperamento, esto será simplemente falso.

guarida: Esta es exactamente la lógica de anillo de la que estoy hablando: si eliges música creada en un sistema específico, es obvio que en su contexto un sistema diferente es imposible.

Para estos y otros comentarios similares, citaría 2 contraargumentos:

1) si con suficiente precisión la igualdad $log_2 {3} = 19/12$ , entonces sería imposible "jalar" un sistema de temperamento uniforme en un sistema puro que consta de 12 sonidos. El mas fuerte $log_2 {3}$ diferente de $inline$ , cuanto más falso sonaría nuestro quinto. Si este número fuera (fuertemente) diferente, entonces no habría un enfoque uniformemente temperamental a los intervalos puros y, como resultado, no habría música moderna o, digamos, sería diferente. Por lo tanto, la conclusión de que las propiedades del número es bastante lógica $log_2 {3}$ son la base de la música moderna.

2) el segundo argumento en contra es imposible de justificar lógicamente, y es solo una suposición, pero me parece que todo este razonamiento es digno de atención. Intentemos responder la pregunta: ¿por qué surgió la necesidad de un sistema uniformemente templado? Los comentarios ya han respondido parcialmente. La música en ese momento (el momento de crear un sistema de temperamento uniforme) ya usaba modulaciones y polifonía, que de hecho, en general, ya requería un temperamento uniforme. El problema del sonido "falso" se resolvió por el hecho de que los músicos "ajustaron" ligeramente el sonido durante la actuación. Fue fácil hacerlo para cuerdas (al menos sin trastes), vientos y voces (correcto, si me equivoco, llegué a esta conclusión a partir de sus comentarios). Por ejemplo, para el violín, esto es solo un ligero cambio en la posición de los dedos. Pero tan pronto como fuiste privado de esa oportunidad (clavecín), inmediatamente todo comenzó a sonar mal. Entonces, parece que estas 12 notas aparecieron no solo así, sino como un desarrollo natural de la música hacia esta posibilidad de modulaciones libres y polifonía rica, y esto a su vez es una consecuencia de la invariancia. Fue un desarrollo natural de la música. Es decir, quiero decir que si la invariancia matemática fuera posible no para 12 sonidos, sino, por ejemplo, para 10, entonces nosotros (incluso antes del temperamento uniforme) en nuestra escala tendríamos 10 sonidos (en este caso, estoy hablando de la forma desarrollo de la música europea). Y luego 10 sonidos de temperamento uniforme serían arrastrados a nuestro sistema puro.

Crítica 2. La unicidad de los doce

Hubo muchas críticas sobre la afirmación de que 12 es el único número razonable.

Primero, al comprender la agresividad de esta declaración y el principio de la imposibilidad de una justificación rigurosa, posiblemente reduje el grado de categorización de algunas de las acusaciones en el artículo. Y aun así ...

En este caso, tenemos 2 líneas de crítica.

1) ¿Por qué considero que 19, 24 o 29 (etc.) son inaceptables?

No, no lo creo. Para diferentes instrumentos, existen técnicas para usar sonidos fuera de la escala, por ejemplo, glissando y vibrato. Estas técnicas agregan belleza y naturalidad al sonido. Por lo tanto, incluso con 12 notas, todavía usamos sonidos auxiliares. Si estamos hablando de un entorno, de un sonido inusual, de enriquecer el sonido ... entonces esto está bastante justificado, pero si estamos hablando de tonos básicos, entonces tengo dudas. La música se crea no solo para la élite, sino para la gente común, y para ellos tal graduación (en mi humilde opinión) es innecesaria.

El segundo argumento, y se dio en los comentarios, es, de hecho, la complejidad de crear instrumentos y rendimiento en el caso de una escala larga, aunque tenemos un gran ejemplo de tal instrumento: sitar. Pero trate de tomar una octava (con una mano) en el piano si tiene una escala de 24 sonidos.

2) ¿Pero qué hay de pentatónico?

En todos los países orientales en los que estuve, por alguna razón rara vez escuché música nacional construida en la escala pentatónica. Y todos los músicos del este, a quienes escuché (y amo a algunos), también interpretaron música bastante europea. Aquí hay una cita interesante: "Los compositores académicos han usado el pentatónico como pintura especial desde el siglo XIX para darle a la música un sabor arcaico". El aroma de lo arcaico ...
Sin embargo, en mi opinión, esta música no es moderna, pero no quiero defender esta posición, por lo tanto, en algunos lugares del artículo utilizo el término "música europea moderna". Está claro que esta música (construida en la escala pentatónica) se desarrolló de acuerdo con otras leyes, y no alcanzó la demanda de una polifonía rica y una modulación frecuente y fácil, que apareció en la música europea. Por lo tanto, este artículo obviamente no es sobre pentatónico.

Crítica 3. Música contemporánea

¿A qué llamo música moderna?

Aunque esto suena como una tautología, por música moderna me refiero a música que requiere invariancia, que en el caso de instrumentos con un sistema fijo (por ejemplo, clavecín, piano) conduce a la necesidad de un sistema uniformemente templado (o algo parecido). En el caso de otros instrumentos, por ejemplo, cuerdas sin trastes, todo parece un poco más complicado, porque, en realidad, es posible usar un conjunto de sonidos más grande (que 12). Pero aún así, cuando hablamos sobre el requisito de invariancia, queremos decir que estos sonidos deben estar muy cerca (en frecuencia) de nuestros 12.

Esta definición incluye casi toda la música de piano, clásica europea, jazz, música rock, pop y todos sus derivados. Estoy seguro de que hay excepciones, pero en mi humilde opinión, estas son las excepciones. No veo ninguna razón para discutir sobre esto, porque Todos pueden invertir algo en este concepto.

Crítica 4. Cálculo

Error en los cálculos.

Creo que esta pregunta se elimina. Sin embargo, debo admitir que durante la discusión hice varias declaraciones erróneas sobre asuntos secundarios que no afectaron la conclusión principal del artículo.

PD: No trate este artículo (y haga los requisitos correspondientes) como trabajo académico. :) Este no es un artículo sobre teoría musical. Además, este no es un artículo sobre la historia de la música. En estas áreas, de ninguna manera considero que mi conocimiento sea al menos de alguna manera significativo y admito que puede haber imprecisiones, aunque intenté evitarlas. Aquí se formula un problema matemático simple (de un nivel de complejidad escolar), cuya solución, como me pareció, tiene una interpretación interesante. Con lo que compartí.

El número subyacente de la música moderna.