Amor matemático

Basado en un artículo de Julien Clinton Sprott. Modelos dinámicos de amor. Dinámica no lineal Psicología y ciencias de la vida, agosto de 2004.

Creía armonía en álgebra ...
La teoría de mi amigo es seca, pero el árbol de la vida siempre es verde ...

¿Quién no peleó por este "problema" ... Fue desmantelado en las antiguas tragedias griegas, el gran Shakespeare nos contó la historia de Romeo y Julieta, Andrzej Wajda lo desmanteló desde ambos lados en la Anatomía del Amor. Pero la gente nunca llegó al fondo de la verdad hasta que los científicos tomaron la decisión. Es cierto que no todo parece bastante convincente para los psicólogos. Ellos mismos a veces incluso después de su propio divorcio comienzan a analizar la historia de su amor difunto. Bueno, escribe libros que a veces van como pasteles calientes. ¡Están escritos por expertos! Que puedo decir Casi nada personal, solo negocios ...

Y finalmente, no los poetas con escritores y psicólogos tomaron el amor por la garganta. Las matemáticas son la reina de las ciencias. ¿Es capaz de hacer frente a un problema eterno? Los libros son publicados, por ejemplo, por John Gotman, "The Mathematics of Marriage", y otros autores. Los matemáticos consideran el desarrollo de las relaciones románticas como un proceso dinámico ...

Y todo comienza, como se esperaba, con definiciones. ¿Cómo identificar el amor cualitativa y cuantitativamente? Los investigadores clasifican el problema por tipo: amorío, pasión, fidelidad. Además, cada especie tiene un conjunto complejo de sentimientos. Pero además del amor por otra persona, hay amor por uno mismo, por la vida, por la humanidad ...

Al mismo tiempo, lo opuesto al amor, en el modelo matemático, no puede ser odio, ya que ambos sentimientos pueden coexistir al mismo tiempo. Por ejemplo, a alguien le pueden gustar algunas manifestaciones de una pareja, pero otras pueden ser desagradables. Por lo tanto, no es realista suponer que el amor de un individuo está influenciado solo por sus propios sentimientos, y que los sentimientos del otro compañero no dependen de otras influencias, y que los parámetros que caracterizan la interacción de dos personas permanecen sin cambios y, por lo tanto, excluyen la posibilidad de aprendizaje y adaptación.

La complejidad incluso en un modelo restringido mínimo aumenta dramáticamente cuando se introducen tres o más variables en las ecuaciones de no linealidad y / o.

* Nota: traductor. En mi opinión, tales estudios también pueden revivir las matemáticas en sí mismas, atraer la atención del público, generalmente alejado de esta ciencia abstracta.

Modelo lineal simple

La historia de amor de Romeo y Julieta en el tiempo (t) se puede representar usando las funciones * R (t) - El amor de Romeo por Julieta y J (t) - El amor de Julieta por Romeo.

Luego, un modelo lineal simple de su relación se expresa mediante ecuaciones (1)



ayb - parámetros del estilo romántico de Romeo
cyd - opciones de estilo Julieta
a - caracteriza cómo Romeo está envuelto en sus propios sentimientos
b - cuánto Romeo es abrazado por los sentimientos de Julieta

Uno de los artículos (Gottman et al., 2002) usa el término "inercia conductual" para el primero y la "función de influencia" para el segundo parámetro. Aunque a = 0, la inercia se vuelve mayor. El modelo dinámico en tales condiciones es bidimensional y controlable por las condiciones iniciales y cuatro parámetros, que pueden ser positivos o negativos.

Rinaldi, 1998a, propuso un modelo lineal simple. Al mismo tiempo, se agrega un término libre a cada derivado para tener en cuenta el atractivo (o antipatía con un valor negativo), que cada uno de los socios muestra al otro en ausencia de otros sentimientos. Tal modelo es más realista porque permite que los sentimientos crezcan desde un estado de indiferencia y proporciona un equilibrio que no se caracteriza por una apatía completa. Todo esto se describe de esta manera solo ingresando dos parámetros adicionales. Si bien el estado de equilibrio no apático puede ser muy importante para los individuos en cuestión, esto no cambia la dinámica sino moviendo el espacio de estado RJ.

Estilos románticos

Romeo puede exhibir uno de los cuatro estilos románticos dependiendo de los signos ayb, con la notación dada por el autor de la obra (Strogatz, 1994) y sus alumnos:

1. Deseo apasionado: a> 0, b> 0 (Romeo está envuelto en los propios sentimientos y sentimientos de Julieta).
2. Tipo narcisista: a> 0, b <0 (Romeo está más envuelto en sus propios sentimientos, está separado de los sentimientos de Julieta).
3. Cauteloso (o amante confiable): a <0, b> 0 (Romeo se aleja de sus propios sentimientos, pero los sentimientos de Julieta lo superan).
4. Ermitaño: a <0, b <0 (Romeo está separado de los sentimientos y sentimientos de Julieta).

Dado que cuatro estilos de comportamiento también son posibles para Juliet, existen 16 combinaciones posibles de pares, cada uno con su propia dinámica, aunque la mitad de ellos corresponde a una permutación de R y J.

Las ecuaciones (1) determinan un único punto de equilibrio para R = J = 0, que corresponde a una relación mutuamente indiferente, o la llamada "meseta del amor" (en el modelo de Rinaldi, 1988), con una descripción del comportamiento a través de valores propios (2)




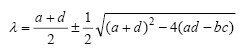
Sillín Focus Forking
Fig. 1. La situación dinámica cerca del punto de equilibrio en el espacio bidimensional, de acuerdo con la ecuación 1.

Triángulo de amor

Se obtiene un modelo matemáticamente más rico cuando se agrega una tercera persona a un modelo simple, en particular porque es posible que se formen alianzas en las que dos individuos pueden unirse contra la tercera. Supongamos que Romeo tiene otro amante, Genevieve, aunque la tercera persona en cuestión puede ser un niño u otro pariente. En este caso, el espacio de estados se vuelve más probable en seis dimensiones que en dos dimensiones, ya que cada uno de los tres tiene sentimientos por los otros dos, y surgen doce parámetros si cada uno puede tomar diferentes estilos en relación con el otro, incluso si se ignora la atracción natural, ( revisado por Rinaldi, 1998a).

En el caso más simple, Juliet y Genevieve pueden no saber sobre la existencia del otro, y Romeo puede mostrar el mismo estilo romántico en relación con ambos. El sistema tetradimensional resultante se transforma en dos sistemas bidimensionales divididos, hasta que los sentimientos de Romeo por Julieta están influenciados de alguna manera por los sentimientos de Genevieve por él, y lo mismo es cierto para Genevieve.

Efectos no lineales

Hay infinitas formas de ingresar efectos no lineales. Imagine que Romeo responde positivamente al amor de Julieta, pero con una manifestación excesiva de su amor, se siente estrangulado y exhibe una reacción adversa. Por el contrario, si Julieta muestra suficiente aversión, Romeo puede intentar ser agradable con ella.

En este caso, es posible reemplazar bJ en la ecuación 1 con la función logística bJ (1 - | J |) correspondiente a la medición de J en unidades a partir de la condición de que J = 1 corresponde al valor en el que su amor se vuelve contraproducente. Resultados cualitativamente similares se derivan de la función bJ (1 - J2), que es el caso considerado por Rinaldi (1998b) para el poeta italiano del siglo XIV, modelo de amor platónico para la bella Laura, vinculada por el matrimonio. Asumiendo lo mismo para Julieta, obtenemos:
(4)



Hay 4 estados de equilibrio, incluido uno en el origen. La Figura 3 muestra el enfoque constante en el que Juliet. como un "deseo apasionado" (c = d = 1) lleva al "ermitaño" de Romeo (a = b = –2) a un estado de amor mutuo en R = J = 2. Un modelo similar para amantes cautelosos (confiables) con no linealidad sigmoidal también conduce a equilibrio estable (Rinaldi y Gragnani 1998). Las ecuaciones 4 obviamente no permiten ciclos límite, y el caos no ocurre mientras el sistema es bidimensional.


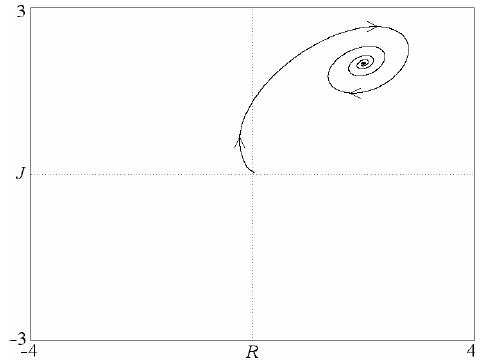Fig. 3. Una de las soluciones para el modelo no lineal según la ecuación 4.

Quizás la aplicación de efectos no lineales a triángulos de amor.

Epílogo

Algunos de los modelos dinámicos lineales del amor exhiben dinámicas sorprendentemente complejas, mientras que muchos de ellos parecen ser similares a la experiencia conocida en las relaciones. Si hay tres o más variables e incluso se introducen los efectos no lineales más simples, puede ocurrir el caos. Se puede imaginar una extensión interesante del modelo al considerar un grupo de personalidades que interactúan, por ejemplo, para casos de una gran familia o comuna. Tales modelos, por supuesto, son muy simplificados, ya que el amor se tiene en cuenta como una variable escalar simple, y las reacciones de los individuos en relación con su propio amor y el amor de otras personalidades por ellos son consistentes y mecanicistas, sin tener en cuenta los factores de influencia externos.

PD: El amor puede vivir sin las matemáticas, pero las matemáticas evocan el amor propio para las personas que valoran la verdadera armonía.

Referencias
Julien Clinton Sprott. Modelos dinámicos de amor. Dinámica No Lineal Psicología y Ciencias de la Vida • Agosto 2004

Rinaldi, S. (1998a). Dinámica del amor: el caso de las parejas lineales. Matemática Aplicada y Computación, 95, 181-192.
Rinaldi, S. y Gragnani, A. (1998). Dinámica del amor entre individuos seguros: un enfoque de modelado. Dinámica no lineal, psicología y ciencias de la vida, 2, 283-301.
Rinaldi, S. (1998b). Laura y Petrarca: un caso intrigante de dinámica cíclica del amor. Revista SIAM de Matemática Aplicada, 58, 1205-1221