La importancia de los números primos, tanto en el uso diario como en todas las ramas de las matemáticas, no se puede sobreestimar . Confiamos tranquilamente en sus propiedades especiales, utilizándolas como la base de innumerables elementos de nuestra sociedad, porque son una parte indivisible de la estructura misma de la naturaleza. Los números primos que son resistentes a cualquier factorización a menudo se llaman "átomos" del mundo de las matemáticas. Carl Sagan dijo sobre ellos así:

El estado de los números primos como bloques de construcción fundamentales de todos los números, que son ellos mismos los bloques de construcción de nuestra comprensión del Universo, es muy importante.

En la naturaleza y en nuestras vidas, los números primos se usan en todas partes: las cigarras construyen sus ciclos de vida sobre ellos, los relojeros los usan para calcular las garrapatas, y en los motores de los aviones, con su ayuda, la frecuencia de los pulsos de aire está equilibrada. Sin embargo, todos estos campos de aplicación se desvanecen en el contexto de un hecho familiar para todos los criptógrafos: los números primos están en el corazón de la seguridad informática moderna, es decir, son directamente responsables de proteger todo . ¿Ves el bloqueo en la barra de direcciones del navegador? Sí, esto significa que se utiliza un "apretón de manos" de dos teclas, basado en números primos. ¿Cómo se protege su tarjeta de crédito cuando compra? También usando criptografía basada en primos.

Sin embargo, a pesar del hecho de que confiamos constantemente en sus propiedades únicas, los números primos se nos escaparon. A lo largo de la historia de las matemáticas, las mentes más grandes han intentado probar un teorema para predecir números que son primos, o qué tan separados deberían estar el uno del otro. De hecho, algunos problemas no resueltos, como el problema de los números gemelos , el problema de Goldbach , los primos de palíndromo y la hipótesis de Riemann , están asociados con esta imprevisibilidad e incertidumbre general de los números primos cuando tienden al infinito. Por supuesto, desde la época de Euclides descubrimos algoritmos que nos permiten predecir la ubicación de algunos números, pero los teoremas generales aún no se han probado y los intentos anteriores no tenían herramientas para verificar números grandes. Sin embargo, la tecnología del siglo XXI permite a los investigadores probar suposiciones en números extremadamente grandes, pero esta técnica por sí sola es controvertida, porque el examen preliminar no se considera evidencia confiable. En otras palabras, los números primos se resisten a obedecer cualquier fórmula o ecuación universal, y su disposición en la naturaleza parece aleatoria.

Sin embargo, una persona con garabatos al azar logró demostrar que al menos no son completamente al azar ...

De garabatos a punta: mantel Ulam

Una de las mejores pruebas de que la disposición de los números primos no es pura coincidencia apareció de la manera más improbable: de garabatos irreflexivos y aleatorios de un estudiante aburrido de conferencias.


Mantel Ulam

Según la historia, el matemático polaco Stanislav Ulam descubrió este patrón gráfico durante un seminario en 1963. Dibujando una cuadrícula de líneas, decidió numerar las intersecciones en un patrón de espiral cuadrada y comenzó a rodear los números en espirales que eran simples. Para su sorpresa, los números primos en círculo cayeron en líneas rectas diagonales o, como Ulam lo expresó un poco más severamente, "mostraron un comportamiento fuertemente no aleatorio". El mantel de Ulam, o espiral de primos, es la visualización gráfica resultante del conjunto de primos marcados en una espiral cuadrada. El mantel fue publicado originalmente y se hizo ampliamente conocido en el título "Juegos matemáticos" por Martin Gardner en Scientific American .


Mantel Ulam de 377x377 (números de hasta aproximadamente 142 mil)

La visualización que se muestra arriba obviamente revela patrones notables, especialmente a lo largo de las diagonales. Pero tal vez nos estamos engañando a nosotros mismos? A menudo se afirma que el mantel de Ulam es solo un truco de nuestro cerebro tratando de encontrar patrones al azar. Afortunadamente, podemos usar dos técnicas diferentes para asegurarnos de que este no sea el caso. Tanto la comparación visual como el análisis lógico definitivamente nos dicen que el patrón no es accidental. Primero, comparamos el mantel Ulam definido por una matriz de tamaño NxN con una matriz del mismo tamaño que contiene puntos definidos al azar. En segundo lugar, podemos usar nuestro conocimiento de polinomios para comprender por qué deberíamos esperar que aparezca algún patrón al mostrar gráficamente números primos.

Como se mencionó anteriormente, lo más probable es que la confirmación más intuitiva de la no aleatoriedad del patrón sea una comparación directa con el mantel de Ulam. Para hacer esto, cree un mantel Ulam y una espiral cuadrada con ubicaciones aleatorias del mismo tamaño. A continuación se muestran dos matrices diferentes de 200x200 que representan espirales numéricas:


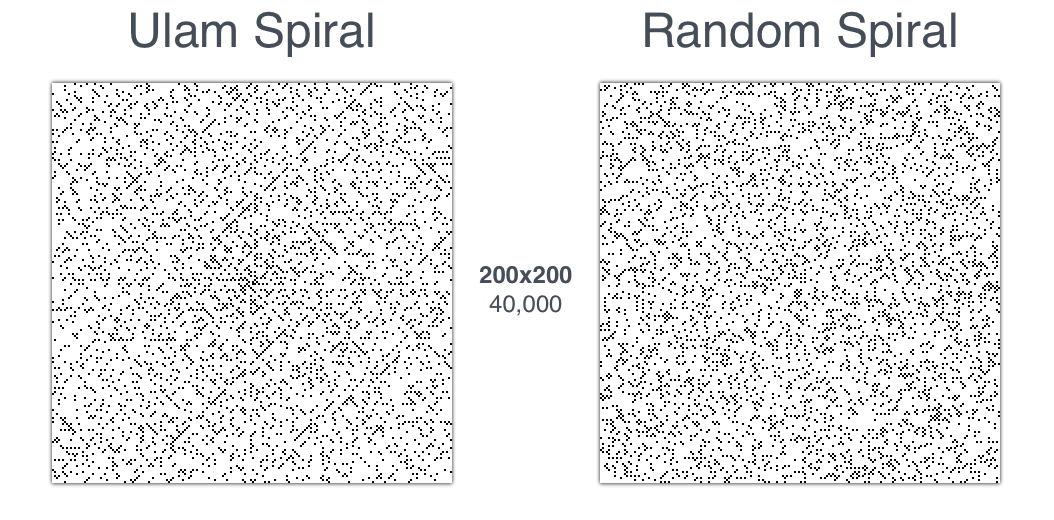
Una comparación visual hace bastante obvio que el mantel de Ulam contiene patrones impresionantes, especialmente a lo largo de los ejes diagonales; Además, casi no hay grupos de puntos en él. Por otro lado, la disposición aleatoria de los puntos no crea inmediatamente patrones notables y conduce a la acumulación de puntos en diferentes direcciones. Indudablemente, tal técnica carece del rigor de la evidencia tradicional; sin embargo, hay algo impecable en la visualización de espirales de números primos: esta es una técnica descubierta al azar que le permite crear un gráfico que estimula la lógica y es atractivo estéticamente.

Si nos acercamos a la naturaleza de los números primos de una manera más lógica y tradicional, entonces es bastante razonable esperar la aparición de patrones en tales visualizaciones. Como se indicó anteriormente, las líneas en dirección diagonal, horizontal y vertical parecen contener una pista. Algunas de estas líneas, que no son números primos, pueden explicarse por polinomios cuadrados ordinarios que excluyen la posibilidad de la aparición de números primos; por ejemplo, una de las líneas diagonales correspondientes a la ecuación y = x² obviamente excluye los números primos. Por otro lado, se sabe que algunos polinomios cuadrados, llamados fórmulas primas (hablaremos de ellos a continuación), crean una alta densidad de primos, por ejemplo, el polinomio primo de Euler: x² - x - 41; Esta es otra línea reflejada como un patrón en espiral (aunque es difícil encontrar huecos en el diagrama anterior).

Una comparación visual indica patrones, y un análisis lógico confirma la existencia de patrones esperados. Por supuesto, todavía estamos lejos de una fórmula universal para encontrar todos los primos, pero el mantel de Ulam es indudablemente hermoso, tanto como un símbolo de nuestro conocimiento y como una obra maestra del arte natural.

Espiral de Sachs

Como en muchas áreas de las matemáticas, después del advenimiento de la idea original, el ejército de compañeros matemáticos que siguieron los pasos comenzó a intentar contribuir al nuevo tema. Es lógico que el mantel de Ulam haya inspirado a generaciones de matemáticos que intentaron desarrollar su sorprendente hallazgo. En 1994, el ingeniero de software Robert Sachs decidió usar sus habilidades de programación para visualizar primos de varias maneras.

Casi como en el caso del mantel de Ulam, Sachs decidió estructurar su esquema usando otro plano espiral. De manera similar a la espiral cuadrada que se muestra arriba, los planos espirales se niegan a dar puntos al sistema de números cartesiano tradicional, porque son un sistema de posicionamiento unipolar . Solo conociendo el número, puede averiguar su ubicación en la espiral, su posición con respecto a todos los demás números en la espiral, así como la distancia desde él hasta el cuadrado anterior y siguiente del número. Sin embargo, en lugar de una espiral cuadrada, Sax intentó encontrar patrones usando enteros superpuestos en una espiral de Arquímedes con las siguientes coordenadas polares:


Coordenadas polares de la espiral de Arquímedes / Sachs

Con esta técnica, la espiral de Arquímedes se centra alrededor de cero, y los cuadrados de todos los números naturales (1,4,9,16,25) se ubican en las intersecciones de la espiral y el eje polar (ubicado al este del origen).


Arquímedes / saxo estructura en espiral

Una vez preparado este diagrama, rellenaremos los puntos entre los cuadrados a lo largo de la espiral (en sentido antihorario), aplicándolos a una distancia igual entre sí. Y al final, como en el ejemplo con el mantel de Ulam, seleccionaremos los números primos contenidos en la espiral resultante.

La espiral numérica de Sachs, publicada por primera vez en línea en 2003, es atractiva tanto visual como intelectualmente. Además, como veremos pronto, nos da una comprensión más profunda de los patrones primarios que el conocido mantel Ulam , porque combina las líneas discontinuas de la pseudo- espiral de Ulam :


Espiral de Arquímedes con números primos marcados, también es la espiral de Sax.

El cuadro resultante muestra nuevamente patrones notables. Casi de inmediato, queda claro que hay una línea blanca limpia que se extiende desde el centro y se extiende horizontalmente hacia el este. Volviendo a nuestro esquema, podemos asegurarnos de que esta sea solo una línea que contiene todos los cuadrados de los enteros (r = n ^ (. 5)). Segunda observación: el patrón de marcado, en contraste con las líneas rectas del mantel Ulam, es más como líneas curvas . Resulta que estas curvas, también conocidas como curvas de producto , nos devuelven a polinomios que explican los patrones que surgen en la espiral anterior. Pero antes de recurrir a ellos, por el bien de la unidad, comparamos nuevamente la espiral de Sachs con la espiral de valores aleatorios:

Polinomios y curvas de producto

El trabajo de Robert Sachs después de este descubrimiento se centró por completo en estas obras curvas , comenzando en el centro de la espiral o al lado, e intersectando en diferentes ángulos con las vueltas de la espiral. Las curvas son casi rectas, pero lo más típico para ellas es que realizan giros en sentido horario parcial, total o múltiple (contra el movimiento de la espiral misma) alrededor del origen, antes de enderezarse en un cierto desplazamiento del eje este-oeste. Uno de los aspectos más llamativos de la espiral numérica de Sachs es el predominio de tales trabajos curvos en el hemisferio occidental (en el lado opuesto al cuadrado de los números).

Sachs describió las curvas de producto como representando "productos de factores con una diferencia constante entre ellos". En otras palabras, cada curva se puede representar mediante una ecuación cuadrática (polinomio de segundo grado), que nuevamente no es una simple coincidencia, dada la prevalencia del cuadrado de un número natural en la espiral de Sachs. Quizás estas curvas de producto nos pueden llevar a la conclusión de que la espiral de Sachs es mucho más útil en nuestro camino para comprender los números primos que el mantel de Ulam. Aunque el mantel de Ulam nos mostró los patrones y la posible existencia de ecuaciones, la espiral de Sachs brinda puntos de apoyo en la búsqueda de fórmulas primarias: su curvatura e integridad son constantes, lo que significa que serán mucho más fáciles de detectar. Por ejemplo, la espiral de Sachs que se muestra a continuación contiene líneas etiquetadas y su fórmula principal correspondiente, escrita en forma estándar. Como prometí, la famosa fórmula de Euler para generar números primos volvió a reunirse con nosotros (última entrada: n² + n +41):


Gracias a esta espiral numérica, Sax pudo hacer una declaración sorprendente sobre qué es un número primo: un número entero positivo que se encuentra en una sola curva del producto. Dado que la espiral puede girar sin fin, las curvas mismas también pueden considerarse infinitas; teóricamente, estas curvas de producto posiblemente pueden predecir la ubicación de números suficientemente grandes; al menos, dichos números merecen una mirada más cercana.

En general, la espiral de Sachs sin duda nos impulsó a una comprensión más profunda de los números primos al proponer fórmulas más convenientes para los números primos.

Significado de todo

Entonces, analizamos tanto el mantel de Ulam como la espiral de Sax. A través de estos ejemplos, nuestra comprensión de la naturaleza de los números primos se ha expandido. En particular, la espiral de Sachs nos introdujo a las curvas de producto, que son esencialmente un conjunto de ecuaciones cuadráticas, conocidas como fórmulas primas. Ambas gráficas, Ulama y Sax, resultaron inesperadas y estéticas, estimulan nuestra curiosidad y arrojan luz sobre una de las tareas más difíciles para todo el mundo.

¿Qué lección se puede aprender de todo esto?

Nunca puede negarse a revisar problemas aparentemente insolubles, incluso si lo hace por pura curiosidad y aburrimiento; todos pueden hacer descubrimientos y, a menudo, surgen como resultado de procesos completamente inusuales. Cambiando el punto de vista sobre la famosa tarea gracias a la visualización, Stanislav Ulam está un paso más cerca de comprender los números primos: ¿quién sabe qué otros descubrimientos inesperados encontraremos?