Fórmula para calcular números primos y optimizar divisores de fuerza bruta

Saludos! En mi tiempo libre decidí investigar el problema de encontrar números primos. El tema es extenso e interesante. Quiero compartir un par de pensamientos al respecto que me vinieron a la mente. Una búsqueda en Internet no reveló tal, señalando su originalidad.

En primer lugar, nunca he encontrado una fórmula matemática para calcular primos en orden. Pero después de todo, si hay algoritmos, entonces es posible componer fórmulas usando funciones lógicas u operadores. Doy a continuación la fórmula más concisa que resultó.

Para alguna secuencia de números $$$(x_ {m}) = {x_ {1}, x_ {2}, x_ {3}, ... x_ {max}}$ Introducimos el operador de detección del primer número igual a a:

$$

$$\ mathbf {Dt_ {a}} (x_ {m}): = \ left \ {\ begin {matrix} m \ \ mathbf {if} \ \ exist \ m: \ forall \, k <m \ x_ {k } \ neq a \ \ mathbf {y} \ x_ {m} = a \\ 0 \ \ mathbf {de lo contrario} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ end {matrix} \ right.$$

Todos los números primos, comenzando con 5, se pueden calcular mediante la fórmula:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} ((P_ {n-1} + 2i) \, mod \, P_ {j + 1})), \ \ \ \ forall \, n \ geqslant 3 \\ \ forall \, i_ {max} \ geqslant \ max \ frac {P _ {\ alpha} -P_ { \ alpha -1}} {2} +10 \ ,, \ \ 2 \ leqslant \ alpha \ leqslant n-1; \ \ j_ {max} = \ pi (\ sqrt {P_ {n-1} + 2i}) - 1$$

Operador $$$\ mathbf {Dt_ {0} ^ {j}}$ itera sobre $$$j$ el resto de dividir cada número de candidato por simplicidad con $$$i$ numero $$$(P_ {n-1} + 2i)$ a primos ya encontrados en el rango hasta $$$P_ {j_ {max} +1}$ . Los números candidatos se seleccionan en orden del conjunto de números impares mayores que el número primo anterior $$$P_ {n-1}$ . $$$\ pi (\ sqrt {P_ {n-1} + 2i})$ Es una función pi que muestra el número de primos $$$\ leqslant \ sqrt {P_ {n-1} + 2i}$ .
Operador $$$\ mathbf {Dt_ {0} ^ {i}}$ itera sobre $$$i$ valores de salida del operador $$$\ mathbf {Dt_ {0} ^ {j}}$ hasta que encuentre 0. Dado que la serie de números primos es infinita, esto sucederá tarde o temprano. A la salida del operador $$$\ mathbf {Dt_ {0} ^ {i}}$ entonces siempre habrá algún número $$$i$ . Límite inferior $$$i_ {max}$ está determinado por la diferencia máxima de primos adyacentes más pequeños que el deseado. El aumento en esta diferencia ocurre logarítmicamente. El siguiente gráfico muestra la dependencia del crecimiento máximo y promedio. $$$\ Delta P _ {\ alpha}$ de n para los primeros 100.000 primos. El valor máximo fue muestreado y promediado para cada mil números.
El aumento máximo en la diferencia de primos $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ al valor máximo anterior $$$max (\ Delta P _ {\ alpha})$ igual a 20 (para la diferencia de primos 31397-31469 = 72 con respecto a la diferencia 25523-25471 = 52). Es en la región donde la derivada del logaritmo de la envoltura $$$\ Delta P _ {\ alpha}$ todavía lo suficientemente grande, y los números primos ya no son demasiado pequeños. Según este valor, la condición para $$$i_ {max}$ . Graph $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ para los primeros 50,000 primos dados a continuación. Los valores se calcularon por cada mil.
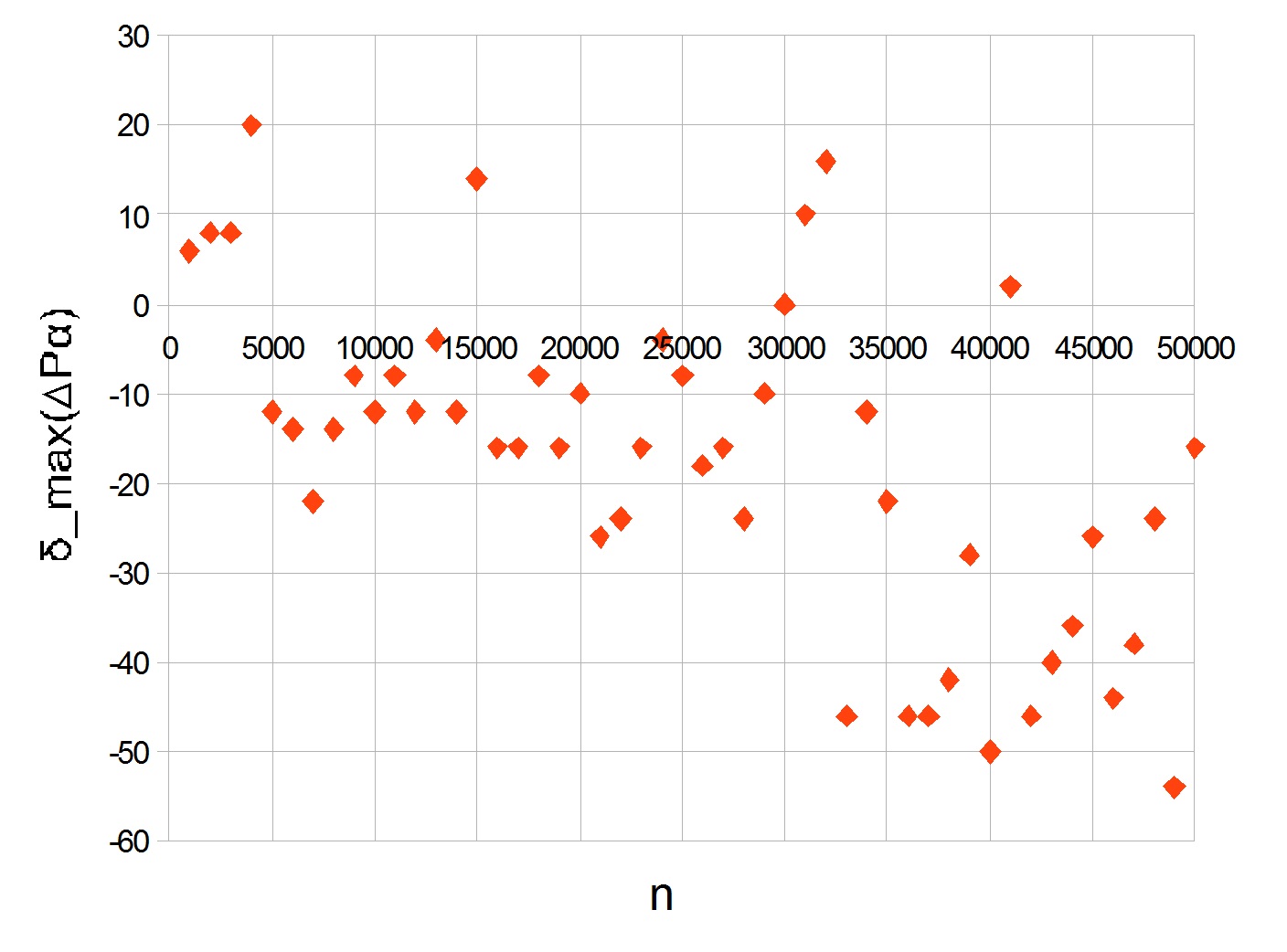
El pico es visible en 20. Con el aumento de n, el gráfico va a menos, mostrando una disminución en la tasa de crecimiento de los números primos grandes.

La segunda consideración es optimizar el cálculo de una secuencia de primos.
El algoritmo establecido en la fórmula anterior es un método mejorado para enumerar divisores. Las mejoras son para excluir números pares de la consideración y verificar la divisibilidad de solo primos más pequeños que sq. Las raíces de los números candidatos. La parte más difícil del algoritmo es el cálculo del conjunto de funciones mod restantes. La complejidad se puede reducir optimizando esta función. Sin embargo, hay una forma aún más efectiva. Dejar $$$(r_ {j + 1} ^ {n-1}) = {r_ {2}, r_ {3}, ... r _ {\ pi (\ sqrt {P_ {n-1}})}}$ Es una secuencia de residuos que divide el último número primo encontrado en primos desde 3 hasta la raíz del mismo. Haremos secuencias de la forma.

$$

$$(r_ {i, j + 1} ^ {n}) = {(r_ {2} + 2i) \, mod \, P_2, (r_ {3} + 2i) \, mod \, P_3, ... \\ (r _ {\ pi (\ sqrt {P_ {n-1}})} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1}})}, (P_ {n -1} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1} + 2i})}}$$

en orden a partir de $$$i = 1$ . El último término se calcula si $$$\ pi (\ sqrt {P_ {n-1} + 2i}) \ neq \ pi (\ sqrt {P_ {n-1}})$ . Cuando en algún paso del cálculo el resto $$$r_ {i, j + 1} ^ {n}$ se vuelve igual a 0, vaya a la siguiente secuencia. Esto se hace hasta que se encuentra, en el que todos los residuos son distintos de cero. Esto significa encontrar el siguiente número primo. Secuencia $$$(r_ {j + 1} ^ {n})$ debe guardarse hasta que se encuentre el siguiente número primo. La fórmula recurrente para calcular números primos de esta manera se convierte a:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} (r_ {i, j + 1} ^ { n})), \ \ \ \ forall \, n \ geqslant 3$$

En el algoritmo presentado, la operación mod es facilitada: divisible por $$$(r_ {j + 1} + 2i) / P_ {j + 1}$ veces más divisores. Las únicas excepciones son la aparición de nuevos divisores simples. En la memoria de la computadora, al implementar el algoritmo, es necesario almacenar una matriz de primos en la raíz de lo buscado, así como una matriz variable de residuos. La complejidad del algoritmo en el sentido general (la cantidad de trabajo) puede ser menor que la de otros métodos conocidos. Las operaciones más complejas en él son la extracción de la raíz cuadrada, el cálculo de residuos y la multiplicación. La raíz se puede extraer al entero más cercano. Para obtener residuos, puede usar un algoritmo efectivo basado en la regla general de divisibilidad. La multiplicación se usa solo por 2 números relativamente pequeños i . La complejidad temporal del algoritmo puede reducirse distribuyendo el trabajo de acuerdo con los valores de i . El tamiz segmentado obtenido de esta manera debería funcionar más rápido en computadoras con múltiples subprocesos. Sin embargo, el trabajo realizado será mayor debido al aumento de los dividendos. También puede "atornillar" la factorización de rueda en el algoritmo. Con el tamaño óptimo de las ruedas, esto puede reducir la complejidad en un cierto rango de n , hasta que el hardware se vuelva más lento.

Tal vez alguien sea útil para mis pensamientos.