Los árboles de búsqueda binarios son una estructura de datos para almacenar elementos con capacidades de búsqueda rápida. La idea es simple e ingeniosa: "menos queda, más es correcto". Aquí es donde termina la simplicidad y comienzan las complejas preguntas de equilibrar un árbol para que no se convierta en una rama larga.

En este artículo, daremos una definición, enumeraremos las reglas para colocar elementos en un árbol rojo-negro, consideraremos el algoritmo de equilibrio y consolidaremos lo que se dijo en un ejemplo. Estudiamos este tema con más detalle, así como otros tipos de árboles de búsqueda binarios en el curso "Algoritmos para desarrolladores" . El árbol rojo-negro
El árbol rojo-negro es un árbol de búsqueda binario autoequilibrado que garantiza un crecimiento logarítmico de la altura del árbol a partir del número de nodos y la ejecución rápida de las operaciones básicas del árbol de búsqueda: agregar, eliminar y buscar un nodo.
El árbol rojo-negro no está completamente equilibrado, en algunos lugares su altura puede variar casi dos veces. Tal suposición no afecta asintóticamente la velocidad de búsqueda de elementos, sino que acelera significativamente la colocación de nuevos elementos, porque no es necesario "sacudir" el árbol cada vez que agrega elementos, a veces es suficiente agregar un elemento rojo sin tocar los otros y sin cambiar la "altura negra" .
Reglas para colocar elementos en un árbol rojo-negro
- Cada nodo es rojo o negro; las hojas NIL siempre son negras.
- La raíz del árbol siempre es negra.
- Ambos descendientes de cada nodo rojo son negros.
- La ruta hacia abajo desde cualquier nodo a cualquier hoja descendente contiene el mismo número de nodos negros.
Cuando inserta un nuevo elemento, se le asigna un color rojo. Para cumplir las dos primeras reglas, simplemente vuelva a pintar los nuevos vértices en el color deseado.
Considere las reglas de equilibrio para la implementación de 3 y 4 puntos.
En cada figura, se supone que ya hemos agregado un elemento X que viola la regla 3, necesitamos cambiar la estructura del árbol para que se ejecute la regla 3 y no se viole el 4.
Leyenda de los vértices:
- X: un elemento agregado que viola 3 párrafos de las reglas.
- P - artículo de papá X
- G - el abuelo del elemento X, el padre del elemento P
- U es el tío del elemento X, el hermano del elemento P, el segundo hijo del elemento G.
Caso uno - Tío rojo
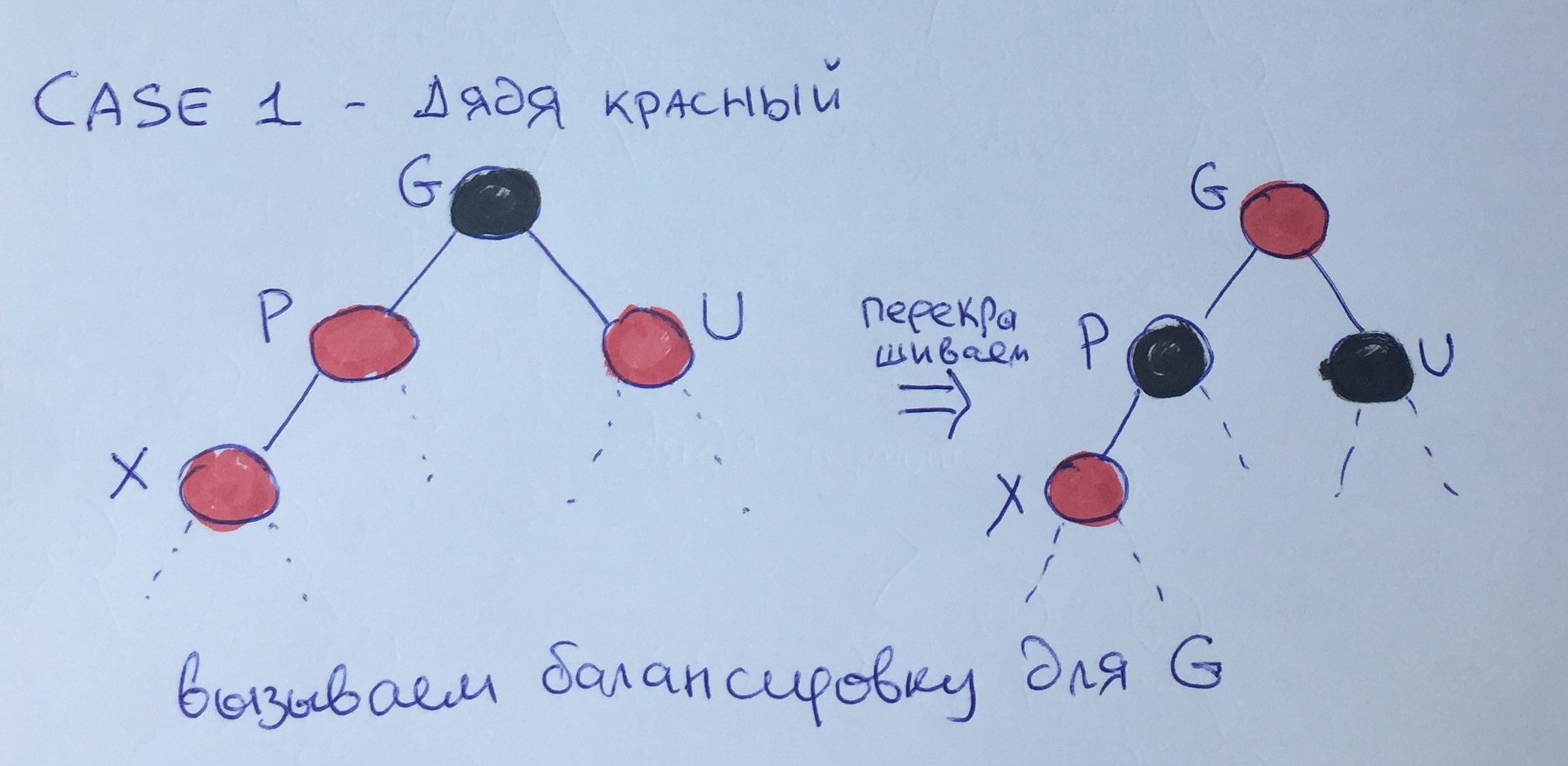
Si tanto el padre como el tío son rojos, entonces podemos "bajar" el color negro del nivel del abuelo al nivel del padre y volver a pintar los nodos como se muestra en la figura. En este caso, la "altura negra" seguirá siendo la misma, sin embargo, es posible la violación de la regla 3 para el elemento G, por lo tanto, es necesario recurrir recursivamente a un mayor equilibrio para este nodo.
Caso dos - un tío negro - papá y abuelo en diferentes direcciones.
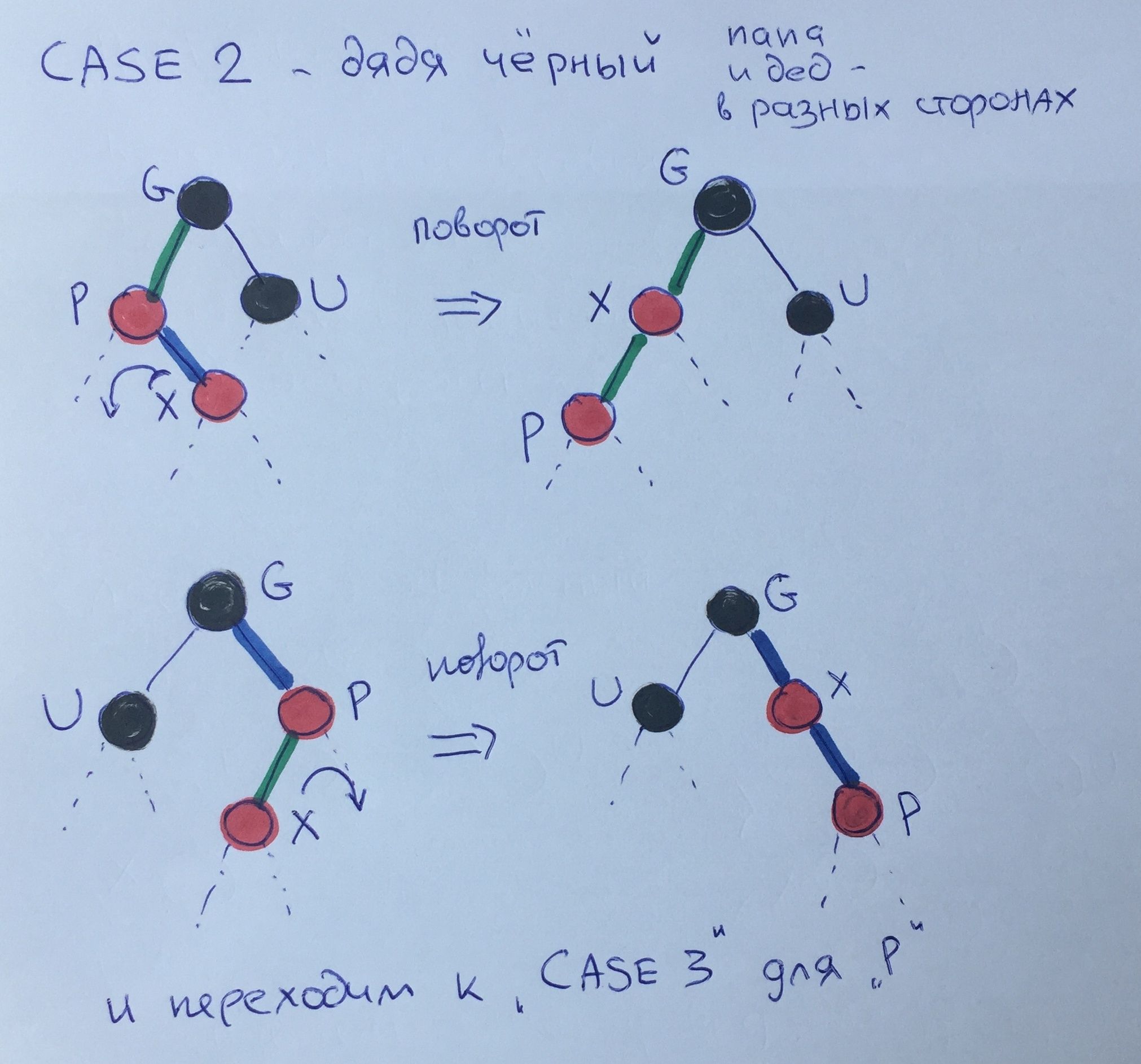
Esta estructura debe llevarse al tercer caso, cuando papá y abuelo van en la misma dirección. Para hacer esto, debe hacer un pequeño giro del hijo X al padre (las reglas de turnos no se consideran en este artículo) y llamar a 3 casos para el elemento R.
Caso tres - Tío negro - Papá y abuelo del mismo lado
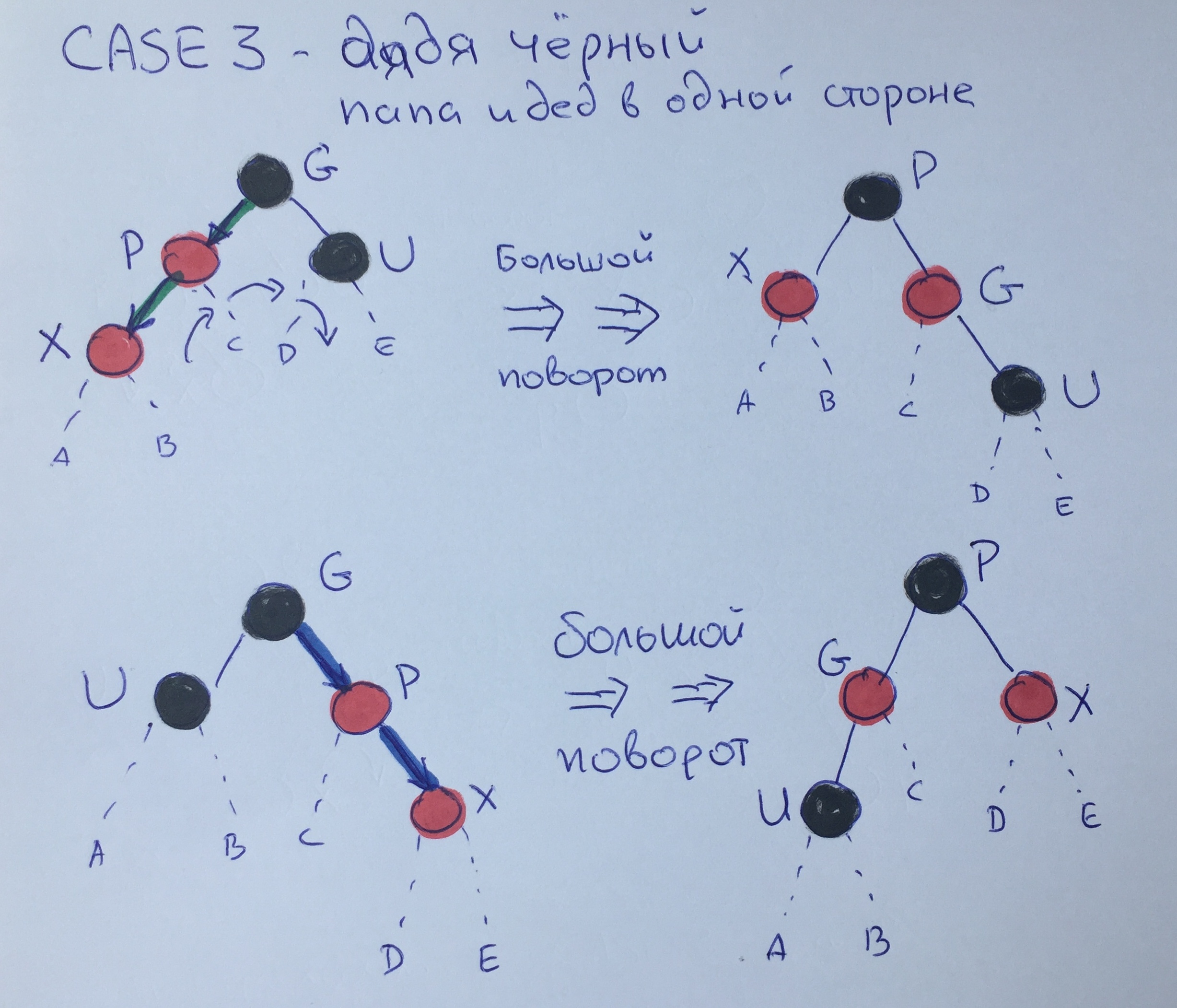
En este caso, ya podemos hacer un gran cambio de padre a abuelo a tío negro y volver a pintar P en negro y G en rojo. Como resultado de esta rotación, se cumplirá la regla 3.
Asegúrese de que la cuarta regla también se cumpla. Suponga que antes del gran giro, la altura negra del elemento G era N + 2. Entonces la altura de los elementos "suspendidos" será la siguiente:
A = N + 1,
B = N + 1,
C = N + 1,
D = N
E = N.
Comprueba por ti mismo que después de convertir la regla 4 es cierto para todos los elementos.
Ejemplo concreto
Ahora consideraremos el proceso de formar un árbol rojo-negro con inserción secuencial de los elementos 1, 2, 3, 4, 5 y 6.
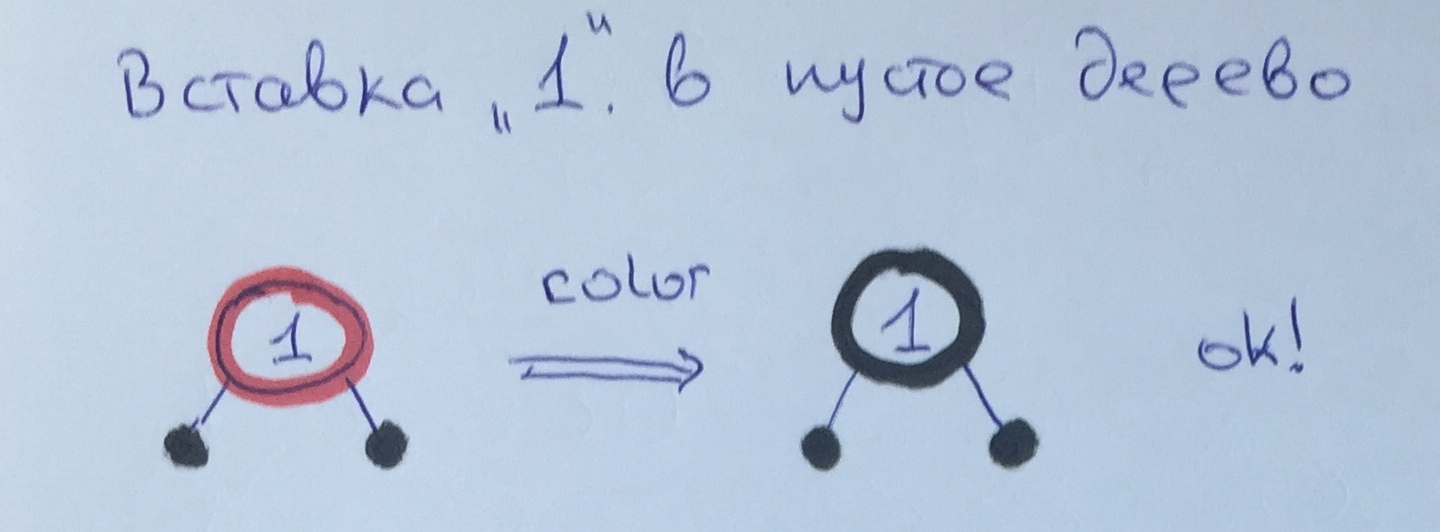
Como el elemento 1 es la raíz, simplemente lo repintamos para cumplir con la regla 1.
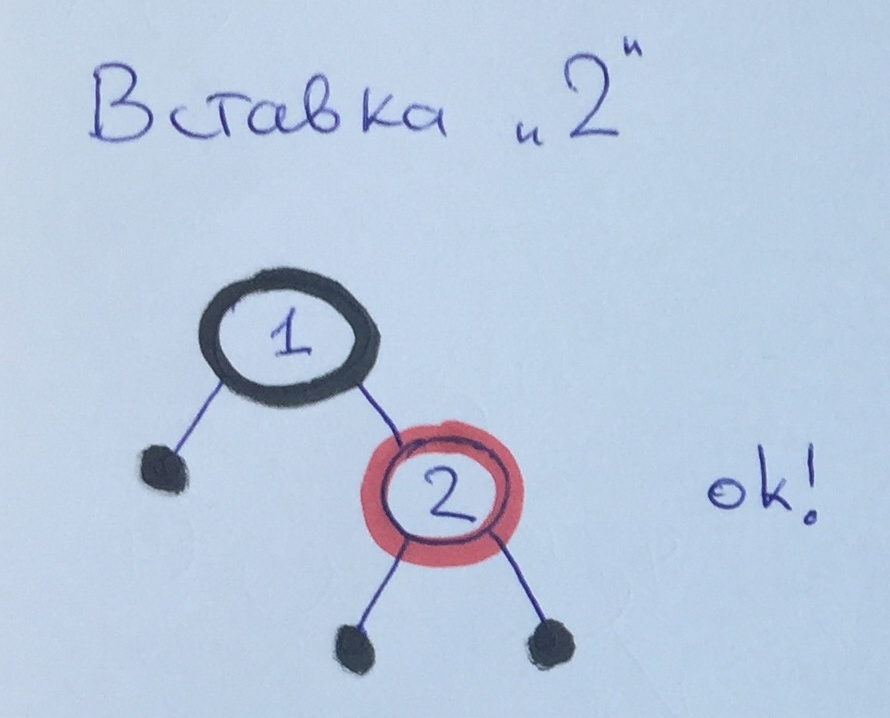
Después de agregar el elemento 2, se ejecutan todas las reglas.
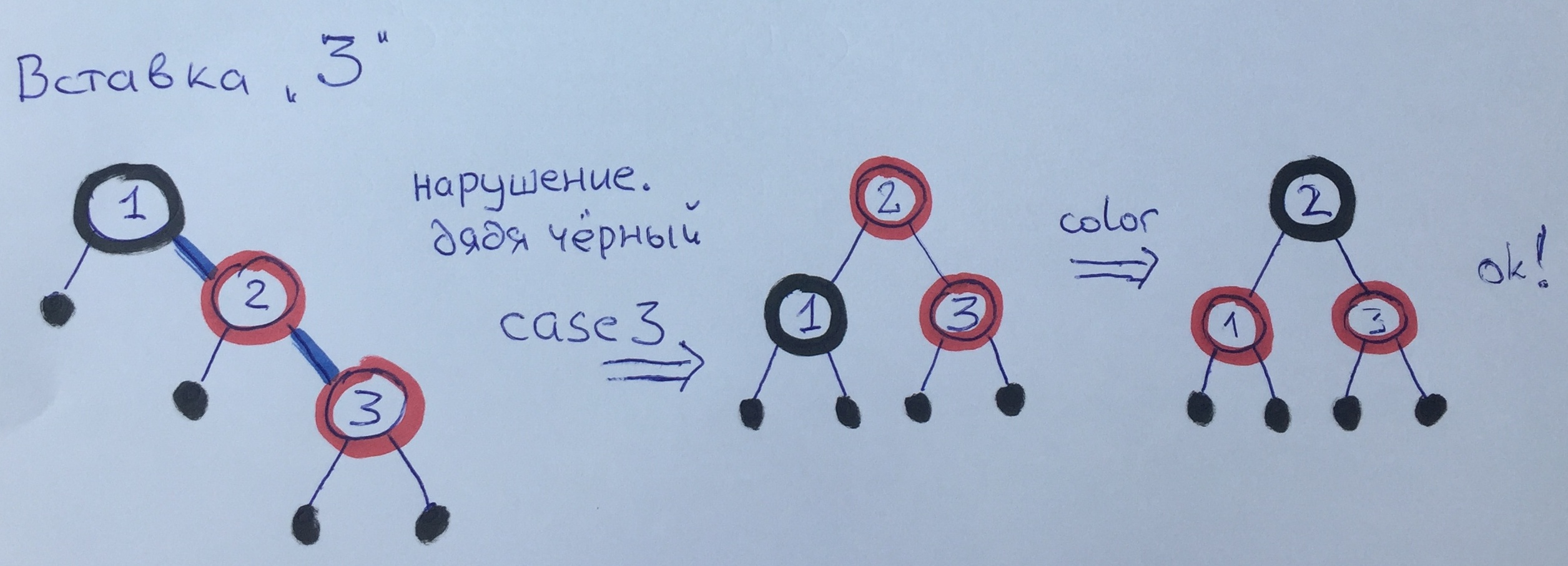
Al agregar el elemento 3, infringimos la regla 3. Como tenemos un tío negro, y un abuelo y un padre, por un lado, usamos el tercer caso: hacemos un giro y repintamos.
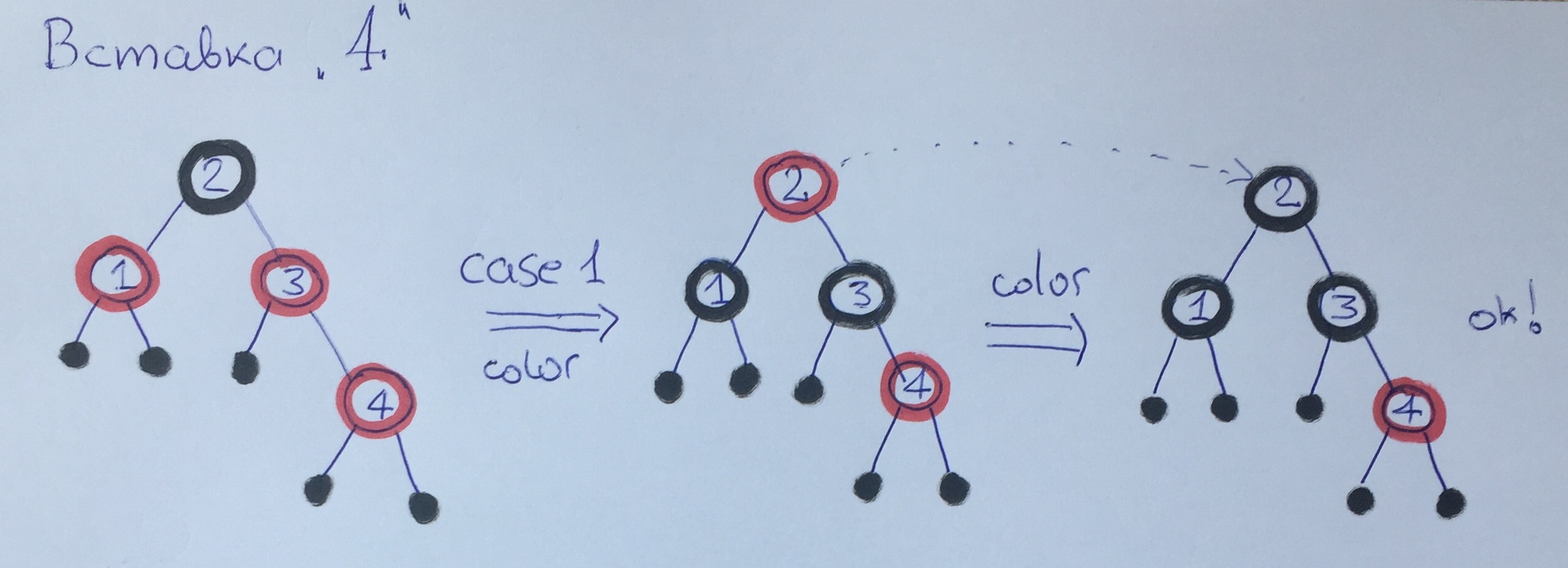
Al agregar el elemento 4, nuevamente violamos la regla 3. Esta vez nuestro tío es rojo, por lo que aplicamos el primer caso con repintado: la altura negra del árbol aumentará en 1. Tenga en cuenta. que el algoritmo de equilibrio se lanza adicionalmente para el abuelo: el elemento 2, que, como la raíz, simplemente se repinta en negro.
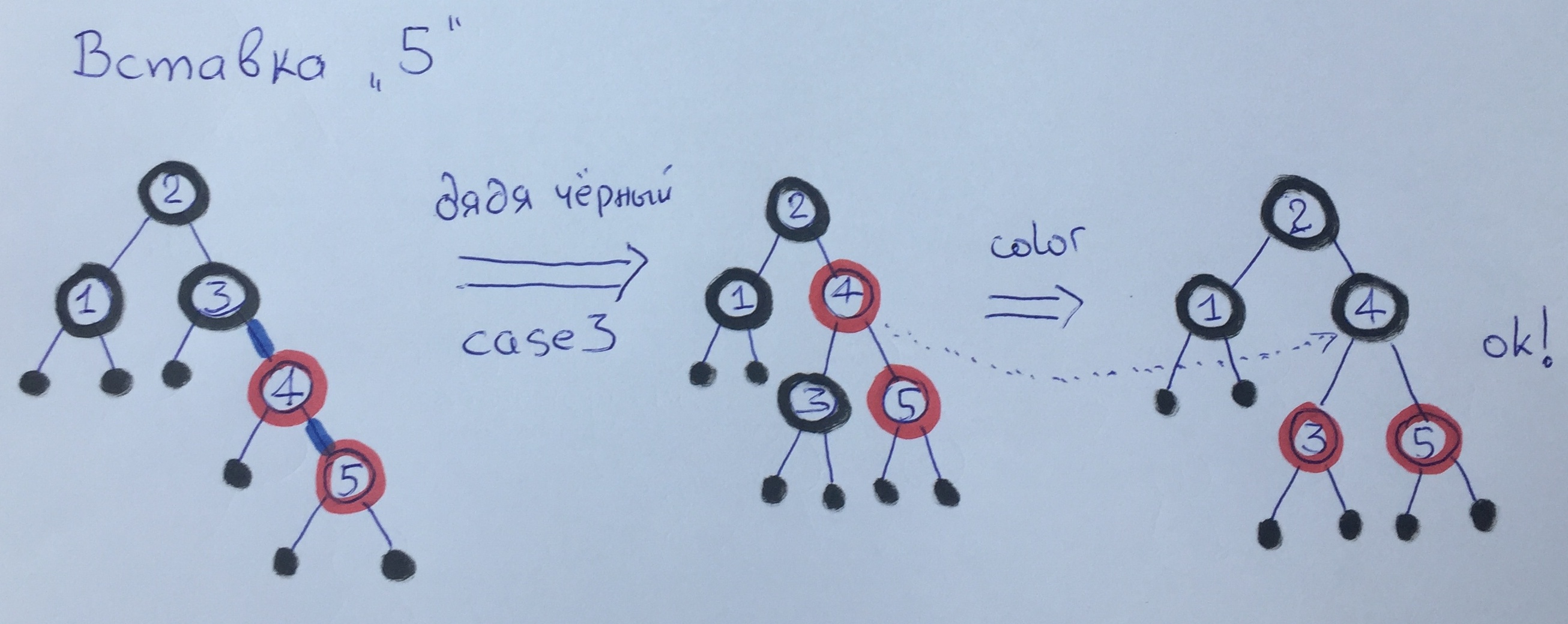
Al insertar el elemento 5, volvemos a aplicar el caso 3: hacemos un gran giro y repintamos los vértices. Tenga en cuenta que la altura del negro no ha cambiado.
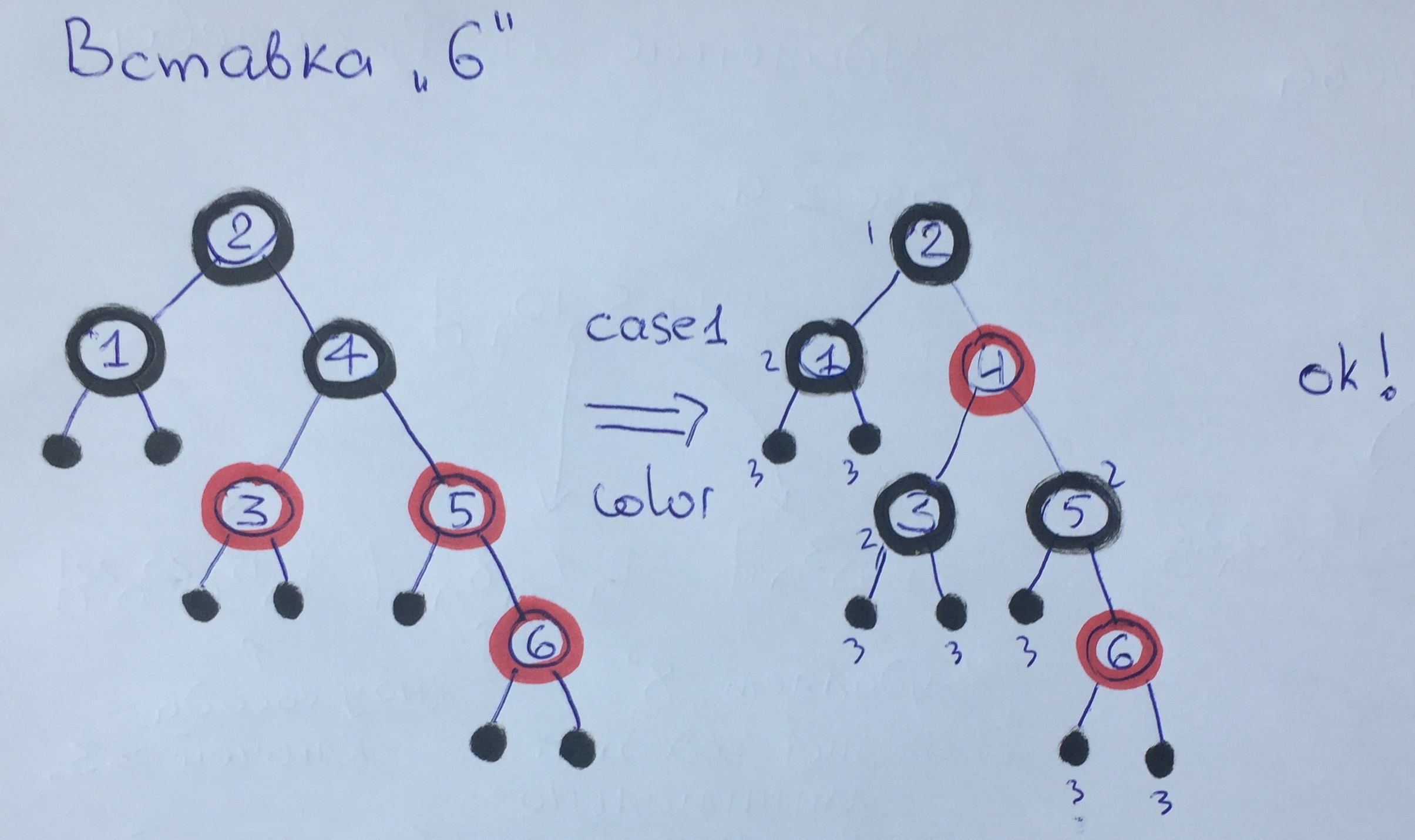
Al agregar el elemento 6, nuevamente violamos la regla 3. Como nuestro tío es rojo, aplicamos el primer caso con repintado, la altura del negro no ha cambiado. La llamada de equilibrio para 4 elementos no cambió nada en el árbol, ya que este elemento no viola las reglas.
Entonces, nos familiarizamos con los problemas de equilibrar el árbol rojo-negro, con más detalle y con ejemplos de algoritmos sobre este tema, así como variedades de otros árboles de búsqueda binarios, que consideramos en el curso
"Algoritmos para desarrolladores" .