Recientemente, se ha escuchado elogios de cada hierro sobre la interpretación multivariada de la mecánica cuántica y negativa hacia Copenhague. Aquí, por ejemplo, un artículo relativamente reciente sobre Habré . Los partidarios de las ideas de los padres fundadores (Niels Bohr, Werner Heisenberg, Paul Dirac, Wolfgang Pauli) ahora se consideran dinosaurios que se niegan a aceptar la interpretación moderna (1957) multimundo.
De hecho, a primera vista, una interpretación multimundo parece lógica y, entre los no iniciados, su conocimiento generalmente causa desconcierto como "¿Cómo se puede discutir con esto? Todavía obvio! ¿Por qué los científicos se aferran a Copenhague? Pero, como siempre, el diablo está en los detalles. Los padres fundadores, a diferencia del alcohólico Hugh Everett, no eran tontos.
Interpretación de Copenhague
La mecánica cuántica es un marco, un conjunto de postulados (axiomas). Diferentes fuentes dan un número diferente de ellos. En algunos casos, algunos postulados pueden deducirse de otros. Pero luego, la presentación del material ya complejo es aún más complicada, por lo que generalmente se formulan 5-6 piezas.
Este marco puede aplicarse a diversas situaciones y desarrollar teorías más detalladas basadas en él: mecánica de partículas cuánticas no relativistas, mecánica cuántica relativista, teoría de campos cuánticos (electromagnética, fuerte, débil, Higgs, etc.), teoría de cuerdas, física de estado sólido y muchos más. de que
La mayoría de los postulados asocian estructuras matemáticas abstractas con la física, por ejemplo:
Los valores observados corresponden a operadores hermitianos.
o
Al medir el valor correspondiente a un operador dado, es posible obtener solo uno de los valores propios de este operador.
o
El estado del sistema (la máxima información posible sobre el sistema) se describe mediante un vector en un espacio de Hilbert llamado vector de estado.
Estos postulados abstractos no se toman del techo, sino del criterio de la correspondencia de las predicciones de la teoría con los datos experimentales. Para una mayor discusión, necesitaremos los siguientes dos postulados. Postulado de medida:
Al medir el valor correspondiente a un operador dado, el vector de estado colapsa en uno de los vectores propios del operador dado, y uno que corresponde al valor propio medido.
y la regla de Bourne:
La probabilidad de que durante la medición obtengamos un valor propio dado del operador es igual al cuadrado del valor absoluto del producto escalar del vector de estado actual con el vector propio correspondiente del operador.
Bastante abstracto, ¿no?
Como señalé, muchos postulados están interconectados. Por ejemplo, el hecho de que un producto escalar debe ser cuadrado, y no en un cubo, digamos, puede deducirse de otros postulados.
Entonces, aplicamos este coloso matemático a la famosa "paradoja" del gato Schrödinger.
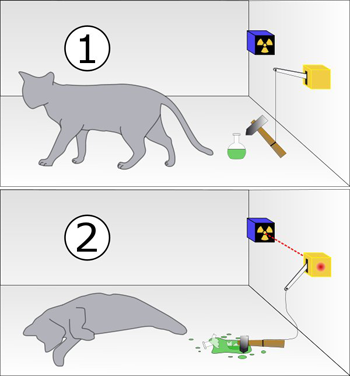
Necesitamos medir el estado del gato (vivo / muerto). Según el postulado, dicha cantidad medida debe corresponder a un operador hermitiano. De hecho, puedes encontrar uno. Los operadores que responden preguntas sí / no (¿el gato está vivo?) Se llaman operadores de proyección. Solo tienen dos valores propios: cero y uno. La unidad en nuestro caso corresponde a un gato vivo, cero a un gato muerto.
Según el postulado, al medir, solo podemos obtener uno de estos dos valores propios. Por lo tanto, nunca vamos a estar vivos + muertos. No existe tal valor propio correspondiente a un vector 
Nuestro operador de proyección. Todo, la "paradoja" está agotada.
Pero la mecánica cuántica también nos permite calcular la probabilidad de que, después de la observación, tengamos un gato vivo y la probabilidad de que esté muerto. Digamos que el vector describe el estado del gato 
. La probabilidad de que, después de la observación, el gato esté vivo, de acuerdo con la regla de Bourne, es igual a:
y el hecho de que está muerto:
Eso es todo, ya terminaron los aburridos cálculos de la mecánica cuántica. Existen teoremas que muestran que, en principio, es imposible extraer más información que estas probabilidades.
Interpretación de mundos múltiples
-
Los partidarios de una interpretación mundial simplemente descartan los dos últimos postulados. No los necesitamos, superfluos.
Pero está claro que si hubieran podido prescindir de ellos, los padres fundadores no los habrían presentado. ¿Con qué los reemplazan los partidarios del mundo múltiple? Curiosamente, en muchos mundos.
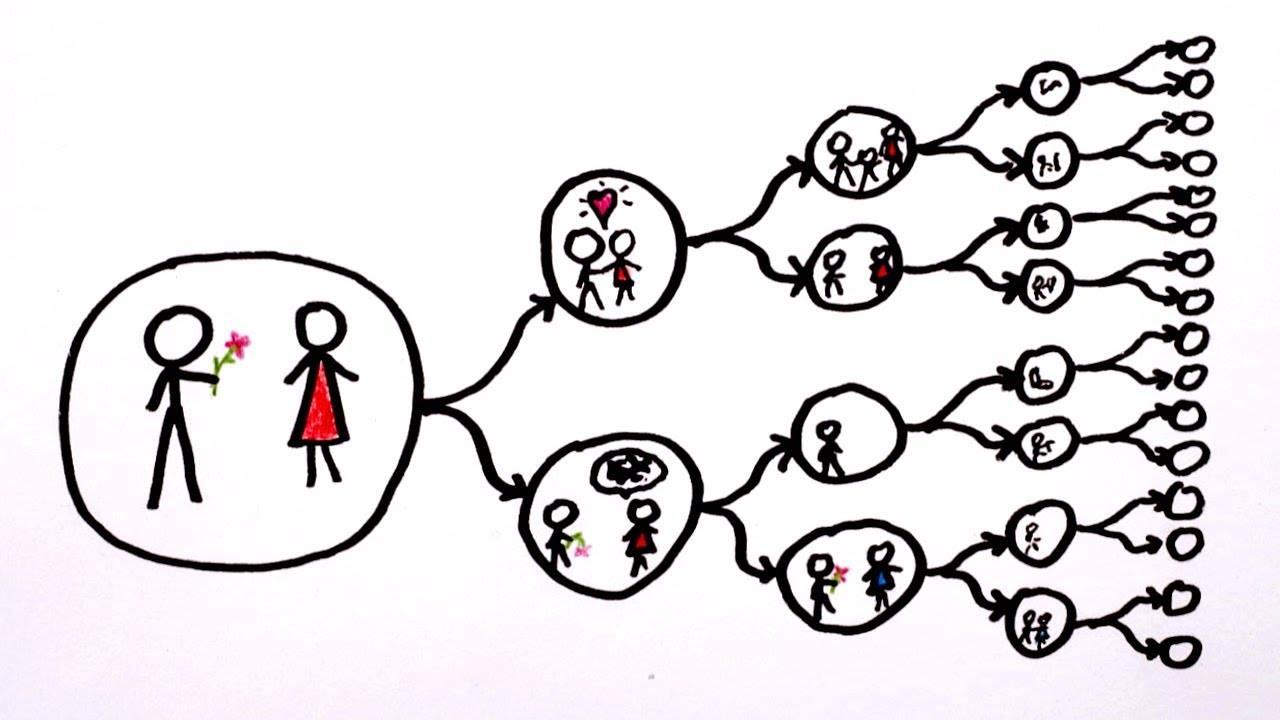
Todas las alternativas se implementan en un mundo particular. Si el sistema es descrito por un vector , entonces el universo se divide en dos mundos: en uno, el gato está vivo, y en el otro, muerto.
-
Brillante, ¿no es así? Y atractivo puramente psicológicamente. Es bueno pensar que hay mundos en los que eres multimillonario.
Pero el mundo múltiple se detiene si solo toma otros coeficientes (amplitudes de probabilidad) antes de los vectores 
y . Toma por ejemplo:
La interpretación estándar de Copenhague dice que cuando se observa con una probabilidad del 99%, veremos un gato muerto. Y créeme, será así. ¿Pero qué ha cambiado en el mundo? Nada Como había dos mundos, permanece. La probabilidad debe ser 0.5.
Los adherentes particularmente avanzados dicen que el "grosor de la rama" ha cambiado. Pero por favor explíqueme de qué depende este grosor y qué lo hace cambiar. ¿Cómo difiere la palabra "grosor de rama" de la palabra "probabilidad"? Aún así, necesita una regla de Bourne, ¿es solo que la probabilidad se reemplaza por el grosor? Bueno ok
En realidad, en la versión original del experimento, el destino del gato está asociado a si el átomo se descompuso o no. La probabilidad de que un átomo se descomponga aumenta con el tiempo, mientras que el hecho de que no se descomponga disminuye. Dentro del marco de la interpretación estándar de Copenhague, incluso se puede encontrar la dependencia exacta de la probabilidad en el tiempo.
Los adeptos de muchos mundos aparentemente resultan que el "grosor de la rama" cambia con el tiempo. En general, un 1% del mundo real y un 99% del mundo real de alguna manera no se ven muy hermosos.
Otro grupo afirma que se formarán cien mundos.
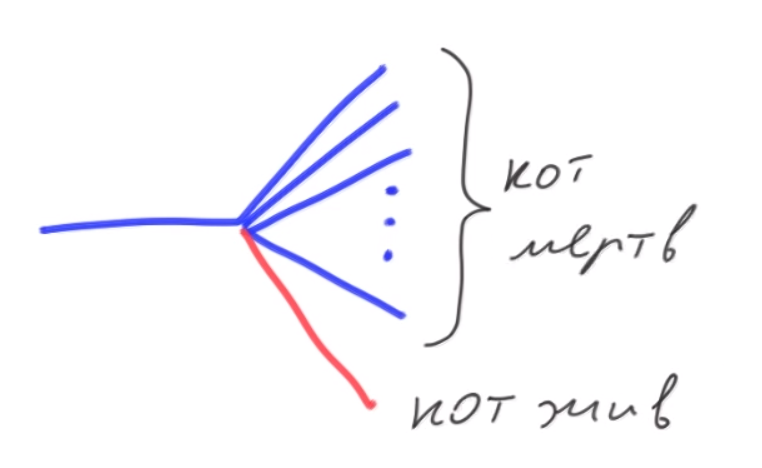
En uno, el gato está vivo, y en 99 muertos. Pero, ¿de dónde provienen los cien, si solo hay dos términos en una superposición: vivo + muerto? Después de todo, se argumenta que una interpretación multivariante no cambia las matemáticas de la MC. Y nuevamente, las probabilidades cambian con el tiempo. Con el tiempo, ¿aparecen más y más mundos con un gato muerto? ¿Incluso si terminara en un mundo con un gato vivo?
Hablando de tiempo. En la representación de Heisenberg, el vector de estado es generalmente estático y los operadores cambian con el tiempo. Pero una interpretación multimundo solo funciona desde el punto de vista de Schrödinger, cuando la evolución temporal se asigna al vector de estado (función de onda). Resulta igual, no es compatible con todas las matemáticas de KM estándar, como se indicó.
¿Cuándo ocurren exactamente estas ramas? ¿Los observadores de diferentes marcos de referencia estarán de acuerdo con el tiempo de ramificación? ¿Alguien ha intentado combinar el mundo múltiple con la teoría de la relatividad?
Otro argumento está asociado con tal matiz de la mecánica cuántica que el observador puede elegir una base en la cual se medirá la cantidad observada. Con el gato Schrödinger, no es del todo obvio qué otra base puede usarse. Pero si consideramos algo "más cuántico", el giro electrónico, por ejemplo, a pesar del hecho de que al medir también obtenemos solo uno de los dos valores (girar hacia arriba o hacia abajo), la forma del operador hermitiano para el giro será diferente para diferentes bases. Y hay infinitamente muchos. Está asociado con la elección del eje con respecto al cual se medirá el giro.
Pero hay infinitas direcciones en el espacio. La distribución de probabilidad de lo que será el giro en la medición depende de la dirección (base) elegida.
Adjuntamos un dispositivo para medir la espalda a un autómata que mata a un gato. Entonces resulta que su destino está conectado con el resultado de medir el giro y la elección del observador de una determinada base. Resulta que el experimentador determina, por su elección, ¿cuántos mundos compartirá el universo?
¿Cuántos mundos se forman? ¿Dos para cada una de las mediciones de giro (arriba / abajo) e infinito para cada una de las bases? ¿Dos veces infinito?
Y si mide alguna cantidad, cuyo operador tiene un espectro continuo. Por ejemplo, a cuál de los infinitos puntos en la pantalla llega el fotón después de pasar una placa de doble rendija.
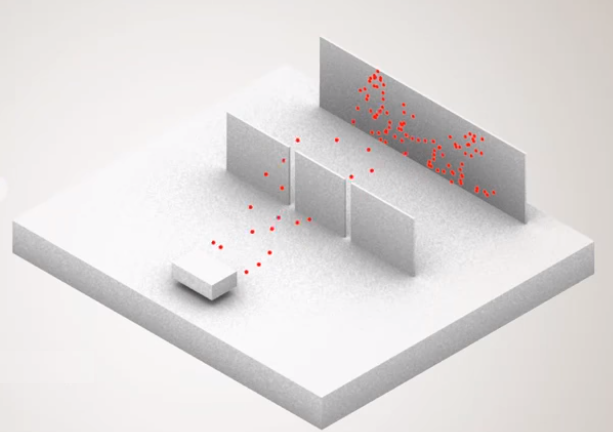
Y si el observador nuevamente quiere cambiar la base. No medirá la coordenada, sino el impulso. ¿Cuántos mundos aparecerán? ¿Infinito multiplicado por dos?
Y si mide una cantidad con un espectro continuo y elige una base, puede hacerlo desde el infinito de posibilidades. ¿Cuántos mundos se formarán? ¿Infinito multiplicado por infinito?
Bien, sé que a George Cantor se le ocurrieron números cardinales y ordinales para tales casos. Idea para fenómenos científicos: intenta describir una interpretación multimundo con ellos. No es de extrañar que existan estos infinitos diferentes en el mundo platónico de las ideas. Al menos lo harán por algo.
Se pueden dar muchos otros argumentos. Por qué y cómo estos mundos pueden unirse de nuevo, y deberían ser capaces de unirse, porque antes de la evolución, la evolución cuántica es reversible. Y dado que los postulados de medición se han eliminado en una interpretación multimundo, la evolución siempre es reversible. ¿Cómo se explican los experimentos de entrelazamiento cuántico? Y así sucesivamente ...
En general, con estas ideas locas, Hugh Everett fue al propio Niels Bohr, quien se rió de él.
Jaja
¿Qué es el colapso?
Los defensores de los mundos múltiples esperan que la regla de Bourne algún día se derive de la "física de la división de los mundos". Las probabilidades no son fundamentales, dicen. Te decepcionaré, pero esto nunca sucederá. Es imposible construir una teoría probabilística sin introducir la probabilidad inicialmente.
Particularmente vehementemente, los adherentes critican el postulado de la medición. Que quiere decir?
Durante la medición, el vector de estado (función de onda) colapsa en uno de los vectores propios del operador de la cantidad medida. En el caso del gato Schrödinger, estos son vectores y . El postulado simplemente dice: cualquiera que sea el vector de estado antes de la medición, si viste un gato vivo, ahora el sistema debería ser descrito por un vector . Si viste un gato muerto, descríbelo ahora con un vector .
Es decir, el colapso refleja la actualización del conocimiento del observador cuando recibe nueva información. Este es un proceso subjetivo. Ningún proceso físico está asociado con el colapso. Y sí, diferentes observadores pueden describir el mismo sistema con diferentes vectores de estado. Y el colapso de ellos puede ocurrir en diferentes momentos. Esto se puede ver en el ejemplo de un experimento mental con un amigo Wigner .
Puedes dibujar una analogía con un lanzamiento de moneda.
Inicialmente, usted describe el sistema con probabilidades: 50%, que el águila caerá, y 50%, que las colas. Pero después de tirar, se cae un águila o una cola. Actualiza su información y describe el estado actual del sistema como 100% de cabezas y 0% de cabezas. Hubo un "colapso" de la distribución de probabilidad en una de las alternativas realizadas.
La mecánica cuántica en su interpretación estándar de Copenhague es subjetiva. Ni un observador ni una observación (medición) pueden ser expulsados.
Feynman en una interpretación multimundo
Richard Feynman se cita comúnmente como un ejemplo de un gurú de la física cuántica. Dedicó una interpretación multivariante de hasta 30 segundos de su vida. Este momento fue guardado como una
transcripción de la conferencia . Feynman expresó el punto de vista de que una interpretación multimundo no tiene sentido y nunca más volvió a ella.