La parte anterior (sobre regresión lineal, descenso de gradiente y cómo funciona todo) -
habr.com/en/post/471458En este artículo, mostraré la solución al problema de clasificación primero, como dicen, "bolígrafos", sin bibliotecas de terceros para SGD, LogLoss y gradientes de cálculo, y luego usando la biblioteca PyTorch.
Objetivo: para dos características categóricas que describen la amarillez y la simetría, determinar a qué clase (manzana o pera) pertenece el objeto (enseñar el modelo para clasificar objetos).
Para comenzar, suba nuestro conjunto de datos:
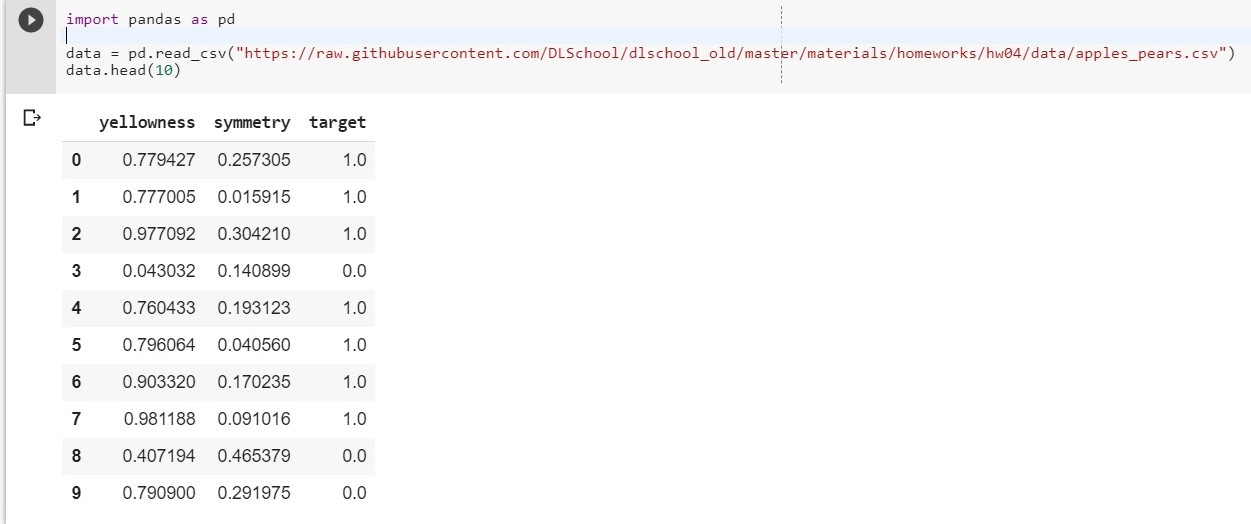
import pandas as pd data = pd.read_csv("https://raw.githubusercontent.com/DLSchool/dlschool_old/master/materials/homeworks/hw04/data/apples_pears.csv") data.head(10)
Dejar: x1 - amarillez, x2 - simetría, y = targer
Componemos la función y = w1 * x1 + w2 * x2 + w0
(w0 se considerará el sesgo (ing. - sesgo))
Ahora nuestra tarea se reduce a encontrar los pesos w1, w2 y w0, que describen con mayor precisión la dependencia de y de x1 y x2.
Usamos la función de pérdida logarítmica:
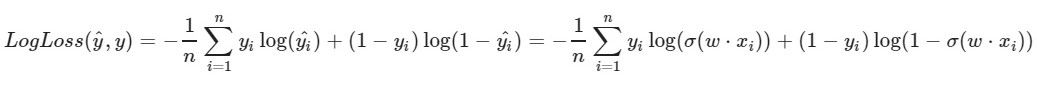
El parámetro izquierdo de la función es la predicción con los pesos actuales w1, w2, w0
El parámetro correcto de la función es el valor correcto (la clase es 0 o 1)
σ (x) es la
función de
activación sigmoidea de x
log (x): el logaritmo natural de x
Está claro que cuanto menor es el valor de la función de pérdida, mejor hemos elegido los pesos w1, w2, w0. Para hacer esto, elija un
descenso de gradiente estocástico .
Observo que la fórmula para LogLoss tendrá un aspecto diferente en vista del hecho de que en SGD seleccionamos un elemento y no una selección completa (o una submuestra, como en el caso del descenso de gradiente de mini lotes):
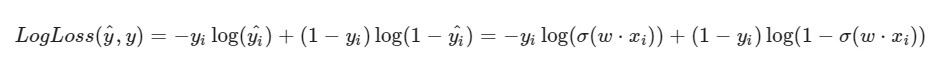Progreso de la solución:Los pesos iniciales w1, w2, w0 reciben valores aleatorios.
Tomamos algún objeto i-ésimo de nuestro conjunto de datos (por ejemplo, aleatorio), calculamos LogLoss para ello (con nuestros w1, w2 y w0, a los que inicialmente asignamos valores aleatorios), luego calculamos las derivadas parciales para cada uno de los pesos w1, w2 y w0, luego actualice cada uno de los pesos.
Un poco de preparación: import pandas as pd import numpy as np X = data.iloc[:,:2].values
Implementación import random np.random.seed(62) w1 = np.random.randn(1) w2 = np.random.randn(1) w0 = np.random.randn(1) print(w1, w2, w0)
[0.49671415] [-0.1382643] [0.64768854]
[0.87991625] [-1.14098372] [0.22355905]
* _grad es la derivada del peso correspondiente. Escribiré la fórmula general:
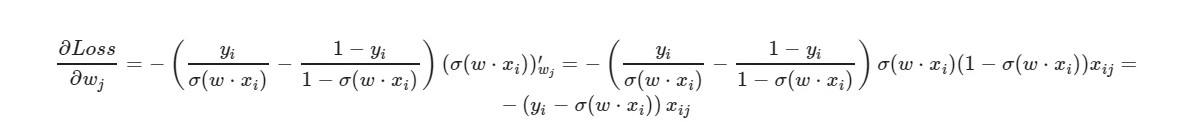
Para el término libre w0, se omite el factor x (tomado igual a uno).
Usando la fórmula final de la derivada, podemos ver que no necesitamos calcular la función de pérdida explícitamente (solo necesitamos derivadas parciales).
Veamos cuántos objetos del conjunto de entrenamiento nuestro modelo da las respuestas correctas y cuántos, las incorrectas.
i = 0 correct = 0 incorrect = 0 for item in y: if(np.around(x1[i] * w1 + x2[i] * w2 + w0) == item): correct += 1 else: incorrect += 1 i = i + 1 print(correct, incorrect)
925 75
np.around (x): redondea el valor de x. Para nosotros: si x> 0.5, entonces el valor es 1. Si x ≤ 0.5, entonces el valor es 0.
¿Y qué haremos si el número de características del objeto es 5? 10? 100? Y tendremos la cantidad adecuada de pesos (más uno por sesgo). Está claro que trabajar manualmente con cada peso, calcular los gradientes para él es inconveniente.
Utilizaremos la popular biblioteca PyTorch.
PyTorch = NumPy +
CUDA + Autograd (cálculo automático de gradientes)
Implementación de PyTorch:
import torch import numpy as np from torch.nn import Linear, Sigmoid def make_train_step(model, loss_fn, optimizer): def train_step(x, y): model.train() yhat = model(x) loss = loss_fn(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() return loss.item() return train_step X = torch.FloatTensor(data.iloc[:,:2].values) y = torch.FloatTensor(data['target'].values.reshape((-1, 1))) from torch import optim, nn neuron = torch.nn.Sequential( Linear(2, out_features=1), Sigmoid() ) print(neuron.state_dict()) lr = 0.1 n_epochs = 10000 loss_fn = nn.MSELoss(reduction="mean") optimizer = optim.SGD(neuron.parameters(), lr=lr) train_step = make_train_step(neuron, loss_fn, optimizer) for epoch in range(n_epochs): loss = train_step(X, y) print(neuron.state_dict()) print(loss)
OrderedDict ([('0.weight', tensor ([[- 0.4148, -0.5838]])), ('0.bias', tensor ([0.5448])]])
OrderedDict ([('0.weight', tensor ([[[5.4915, -8.2156]])), ('0.bias', tensor ([- 1.1130])]])
0.03930133953690529
Pérdida bastante buena en la muestra de prueba.
Aquí,
MSELoss se selecciona como una función de pérdida.
Más sobre linealEn resumen: le damos 2 parámetros a la entrada (nuestro x1 y x2 como en el ejemplo anterior) y obtenemos un parámetro (y) a la salida, que, a su vez, se alimenta a la entrada de la función de activación. Y luego ya están calculados: el valor de la función de error, gradientes. Al final, los pesos se actualizan.
Materiales utilizados en el artículo.