Todo lo que quería saber sobre el péndulo inverso

El artículo sirve como una hoja de trucos para aquellos que desean hacer su péndulo inverso. Estos son los problemas por los cuales volví a trabajar varias veces, se necesita una breve descripción de la teoría para comprender cómo estabilizar el sistema.

¿Por qué necesitaba esto?

En resumen: quería expandir mi máquina CNC, pero algo salió mal ...

Intentos fallidos

El proyecto tomó casi dos años de prueba y error, rediseño, esperando detalles y días de descanso incompletos, de modo que aquellos que desean repetir ahorraron su tiempo y nervios, considero necesario hablar sobre decisiones fallidas.

• un giroscopio (MPU6050) en lugar de un codificador, básicamente nada contra él, pero el sensor debe ubicarse en una varilla giratoria, esto introduce un efecto impredecible y la incapacidad de desplazar la varilla varias veces alrededor del eje.
  
• codificador absoluto: si es un potenciómetro, incluso el movimiento de los cables (principalmente debido a los contactos en el arduino) introduce ruido en las mediciones, un ADC de 10 bits todavía no es suficiente; Si se trata de un sensor más costoso, la lectura se realiza a través de una interfaz en serie, y esto introduce un retraso en el sistema, especialmente en combinación con un motor paso a paso.
  
• La rigidez del sistema: en algún momento tomé un tubo de aluminio con una carga al final, cuando el carro vibró, comenzaron fuertes vibraciones y no estaba claro de inmediato qué sistema estábamos estabilizando. Debemos esforzarnos por garantizar que el sistema físico esté lo más cerca posible de lo que se modela.
  
• fricción: este fenómeno a menudo se descuida, traté de reducirlo usando ruedas de carro grandes y perfiles de ranura en V, en contraste con los rieles con deslizadores con bolas pequeñas, porque La fricción de rodadura es inversamente proporcional al radio.
  
• El uso de un motor paso a paso: pasé mucho tiempo tratando de seguir esta ruta, es engañoso simplificar las fórmulas (de hecho, controlamos de inmediato la aceleración de la base del péndulo) y la simplicidad del diseño (podemos olvidarnos de la fricción en el riel, el codificador del motor, si suponemos que el motor no omite los pasos) , pero ... Para controlar con precisión la velocidad, el tiempo entre pasos debe ser de decenas de microsegundos, lo que significa que puede olvidarse de la salida de estado a la consola. Sin retroalimentación, no puede estar seguro de que el motor no haya perdido los pasos y que la velocidad es realmente lo que piensa el sistema. No afirmo que esta sea una solución sin salida, si alguien logra estabilizar el péndulo con un motor paso a paso, estaré encantado de verlo.
  

Péndulo libre

Para completar la imagen, simulamos un péndulo en un carro libre sin fricción.

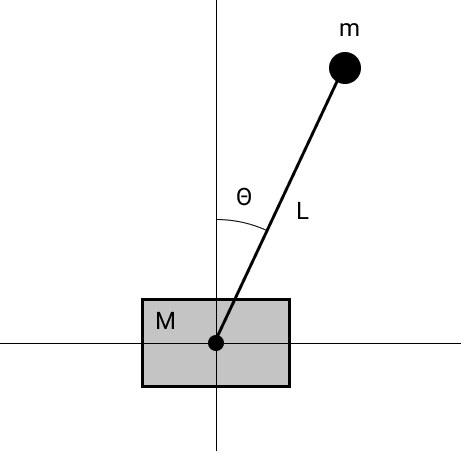
Las ecuaciones de movimiento se pueden obtener diferenciando el lagrangiano con respecto a las coordenadas generalizadas. Obtenemos las siguientes ecuaciones:

$$

$$\ begin {cases} L \ cdot \ ddot \ theta + g \ cdot {sin (\ theta)} - \ ddot {x} \ cdot {cos (th)} = 0 \\ (m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot {sin (\ theta )} = 0 \ end {casos}$$

desde el cual puede encontrar cómo cambia el vector de estado:

$$

$$\ begin {cases} \ dot \ theta = w \\ \ dot {w} = \ frac {g \ cdot {sin (\ theta)} + b \ cdot {L} \ cdot {w ^ 2} \ cdot { sin (\ theta)} \ cdot {cos (\ theta)}} {L \ cdot (1 + b \ cdot {cos ^ 2 (\ theta))}} \\ \ dot {x} = v \\ \ dot {v} = b \ cdot \ frac {L \ cdot {w ^ 2} \ cdot {sin (\ theta)} - g \ cdot {sin (\ theta)} \ cdot {cos (\ theta)}} {1 + b \ cdot {cos ^ 2 (\ theta)}} \ end {cases}, b = \ frac {m} {M + m}$$

y simular el sistema. El codigo esta aqui .

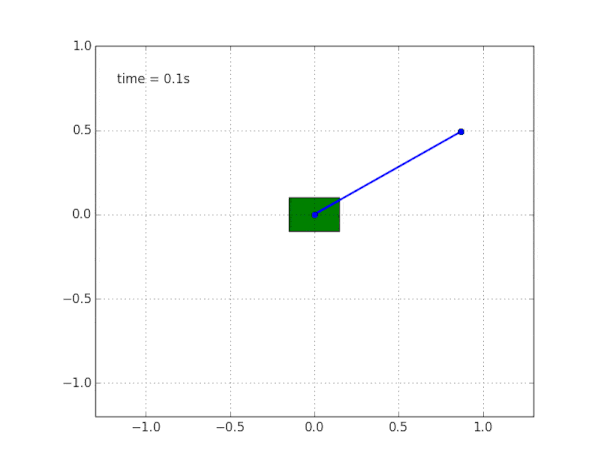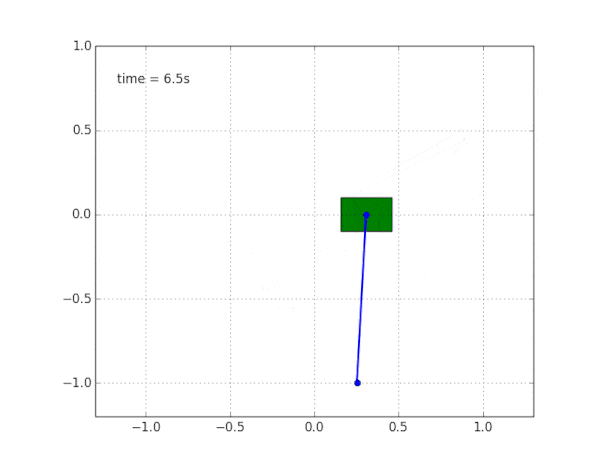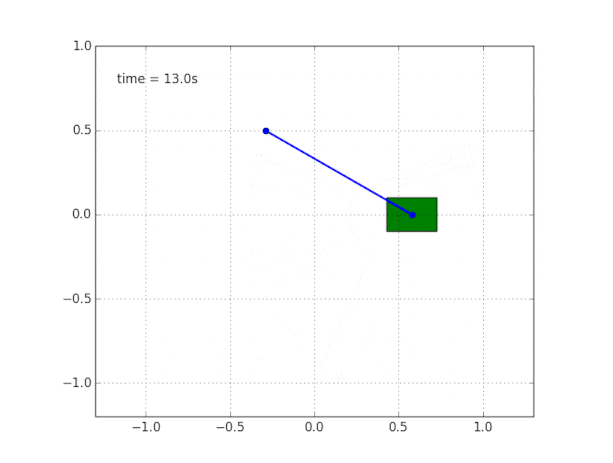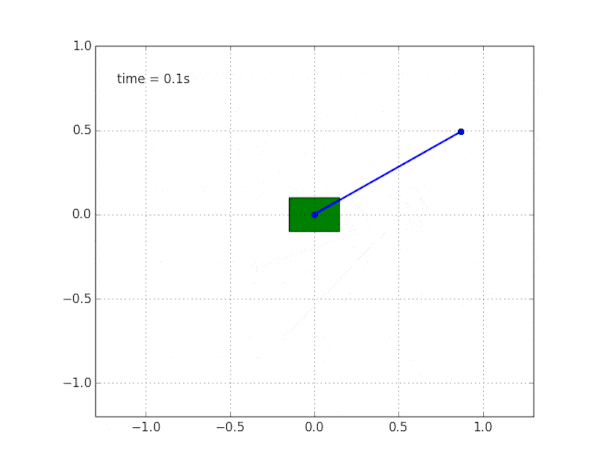
¿Por qué el sistema es inestable?

El sentido común y la visualización nos dicen que el péndulo en sí no se mantendrá. Pero, ¿cómo verificar esto matemáticamente?
En términos generales, el sistema linealizado y la solución son los siguientes:

$$

$$\ dot {\ mathbf {x}} = A \ mathbf {x}, \ mathbf {x} (t) = e ^ {At} \ mathbf {x} (0)$$

Un exponente en el poder de la matriz se ve más claro si va al sistema de coordenadas desde vectores propios, luego $$$A$ será diagonal ( $$$D$ ), y el expositor se verá así:

$$

$$e ^ {Dt} = \ begin {bmatrix} e ^ {\ lambda_1t} & 0 & \ dots & 0 \\ 0 & e ^ {\ lambda_2t} & \ dots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ dots & e ^ {\ lambda_nt} \\ \ end {bmatrix}$$

Ahora se ve, en presencia de valores propios ( $$$\ lambda_i$ ) con una parte real positiva, el componente correspondiente del vector de estado tenderá al infinito y el sistema se desmoronará. Lo anterior se aplica a los sistemas continuos, más sobre la sostenibilidad se describe en esta video conferencia.
Compruebe si este es el caso del péndulo inverso. Linealizamos nuestro sistema cerca de la posición de equilibrio para $$$\ theta = 0, sin (\ theta) \ approx \ theta, cos (\ theta) \ approx 1, w ^ 2 \ approx 0$ :

$$

$$\ begin {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ begin {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ begin {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix}$$

Los autovalores distintos de cero tienen la forma $$$\ pm \ sqrt {\ frac {g} {L (1 + b)}}$ , así nos convencimos de la inestabilidad.

Añadir comentarios

Ahora la fuerza actuará sobre el carro $$$f$ , una de las ecuaciones se puede reescribir en la forma: $$$(m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot {sin (\ theta)} = f$ , y el sistema linealizado tomará la forma:

$$

$$\ begin {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ begin {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ begin {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix} + \ begin {bmatrix} 0 \\ \ frac {1} {L} \ frac {1} {2m + M} \\ 0 \\ \ frac {1} {2m + M} \ end {bmatrix} \ cdot {f}$$

Ahora el sistema ( $$$\ dot {\ mathbf {x}} = A \ mathbf {x} + Bu$ ) se volvió controlable , esto se puede verificar comprobando que el rango de la matriz $$$\ begin {bmatrix} B && AB && A ^ 2B && A ^ 3B \ end {bmatrix}$ igual a la dimensión del vector de estado, es decir 4. Para mantener el péndulo en posición vertical, utilicé un controlador de estado lineal-cuadrático, es decir control (uof) es el producto del vector de estado $$$[\ theta, \ dot {\ theta}, x, \ dot {x}]$ por un vector de parámetros que se encuentran una vez al minimizar la función cuadrática . El código de simulación está aquí .

Control del motor

Ahora necesita controlar el motor de CC, contiene muchos parámetros que no conozco, así que lo tomé como un "recuadro negro", descrito por las siguientes ecuaciones, teniendo en cuenta la fricción:

$$

$$\ begin {cases} \ dot {x} = v \\ \ dot {v} = -a \ cdot {v} + b \ cdot {U} + c \ cdot {sign (v)} \ end {cases} $$$

Puede leer sobre la derivación de ecuaciones y la estimación de parámetros aquí . A continuación doy mis gráficos de la aceleración del motor con el carro dependiendo del voltaje (en realidad, la señal PWM se emite desde el controlador) y las curvas ajustadas.

También encontré coeficientes modelo por fuerza bruta, código .
Por lo tanto, el controlador nos da la aceleración requerida, y a partir de la segunda ecuación, conociendo todas las constantes, encontramos el voltaje.

Poniendo el dispositivo real juntos

Ahora tenemos todo el conocimiento para recolectar y estabilizar el péndulo. Usé el siguiente hierro:

• Arduino Mega 2560 no es UNO, porque dos codificadores necesitan 4 pines para las interrupciones
• El codificador para el péndulo - OMRON E6B2-CWZ6C 2500 pulsos por revolución - nos da el ángulo, calculamos la velocidad angular, la resolución es bastante alta, por lo que hubo suficientes diferencias finitas sin suavizar ni promediar
• Codificador para el motor - LPD3806-600BM-G5-24C 600 pulsos por revolución - da la posición del carro, calcula la velocidad
• Motor de 12 V CC con caja de cambios 5: 1
• Controlador de motor 10Amp 5V-30V

Por lo tanto, medimos explícitamente el ángulo del péndulo, la posición del carro, calculamos la velocidad angular del péndulo y la velocidad del carro; obtenemos el estado completo, encontré los parámetros del controlador con este script. Sorprendentemente, todo funcionó rápidamente como estaba. Estoy satisfecho con el resultado, ¡se destaca e incluso sostiene un vaso!


El código para Arduino está aquí.
Lo que podría mejorarse en comparación con muchas de las opciones que se pueden encontrar en YouTube: este péndulo es silencioso porque el PWM está sintonizado fuera del rango auditivo y se usan ruedas de plástico.
Ahora esta tarea parece un trabajo de laboratorio: medir los parámetros del motor y encontrar los coeficientes del regulador, al mismo tiempo que comprende lo que está sucediendo.

Que sigue

Planeo producir un péndulo: hacer un columpio, deshacerme de una bobina de cables, hacer un escudo con conectores convenientes para que no sea una pena donar a alguna escuela o museo. Si alguien quiere unirse, me alegrará que haya muchas ideas más ambiciosas.

Referencias

• Descripción detallada del problema del péndulo inverso.
• Masticamos un regulador lineal-cuadrático para controlar un péndulo invertido ; este artículo me ahorró mucho tiempo al construir mi péndulo
• Grandes video conferencias de TAU

Gracias por su atencion!