La justificación matemática de lo inapropiado de correr por la escalera mecánica en el metro

Contrariamente a las reglas de uso del metro, para ahorrar tiempo, cada uno de nosotros corrió al menos una vez en nuestras vidas por la escalera mecánica. A primera vista, parece que esto es absolutamente lógico y correcto: si desea irse más rápido, intente estar en la plataforma lo antes posible. Sin embargo, casi de inmediato me viene a la mente el siguiente escenario: baja precipitadamente por la escalera mecánica, baja a la plataforma y las puertas del automóvil se cierran justo en frente de su nariz. Mientras espera el próximo tren, las personas que se subieron a la escalera mecánica al mismo tiempo que usted tiene tiempo de quedarse quieto en silencio bajan y toman el próximo tren. En este caso, no hay ganancia. Entonces, ¿qué tan racional es correr por la escalera mecánica y vale la pena hacerlo? Me apresuro a complacerte: ¡se encuentra la respuesta! A continuación hay una justificación matemática para la falta de habilidad (sí, NO lo es) para bajar corriendo las escaleras mecánicas en el metro.

Declaración de tarea

Antes de pasar al razonamiento matemático, vale la pena mencionar que, naturalmente, no soy el primero en pensar en este tema en absoluto. En Internet puede encontrar un número suficiente de artículos e incluso noticias de canales federales sobre este tema. Sin embargo, cada vez que la esencia de tales experimentos radica en el funcionamiento habitual de la escalera mecánica con la posterior comparación del tiempo ganado con el tiempo de la persona parada en la escalera mecánica. Un poco mejor si los autores intentan evaluar la efectividad del descenso. Aún mejor si todavía proporcionan estadísticas. Para las estadísticas, por cierto, diré un agradecimiento especial un poco más bajo. En relación con la falta de claridad de estos experimentos y la falta de conclusiones prácticas, fui concebido, y posteriormente llevado a cabo, un análisis del proceso en curso.

Y así, formulamos las condiciones del problema y denotamos las restricciones:

1. El experimento (mental) involucra a dos personas que se acercan a la escalera mecánica al mismo tiempo en un momento aleatorio y no tienen idea de dónde está el tren.
2. Una de estas personas está parada en una escalera mecánica y pasa tiempo en un descenso. $$ igual al tiempo de movimiento de la escalera mecánica.
3. El segundo acelera por la escalera mecánica, aumentando su velocidad en $$ veces, reduciendo así el tiempo de descenso en la misma cantidad de veces: $$ .
4. Efectivo se considera un descenso tan acelerado, que condujo al hecho de que la persona que está parada en la escalera mecánica no tiene tiempo para subirse al tren, en el que la persona que escapa en la escalera mecánica tiene tiempo de abordar.
5. Denote por $$ - la probabilidad de un descenso efectivo. Luego, de acuerdo con el equilibrio de Nash, una persona está lista para arriesgarse y correr por la escalera mecánica solo si la probabilidad de un descenso efectivo es mayor o igual a la probabilidad de un descenso o parada ineficaz, es decir, 0.5. Si la probabilidad de un descenso efectivo es mayor o igual a 0.5, la decisión de bajar la escalera mecánica se considerará apropiada . Si es inferior a 0,5, poco práctico .
6. Descuidamos el hecho de que, en la vida real, por regla general, es necesario ir más lejos hasta el automóvil después de salir de la escalera mecánica o esperar a que las personas salgan del automóvil, los trenes circulan a intervalos variables y por un tiempo permanecen inmóviles antes de abrir y después de cerrar las puertas, es decir, asumiremos que si al momento de salir de la escalera mecánica el tren está en la estación, sus puertas están abiertas y el participante del experimento termina instantáneamente en el automóvil, el tren en sí abre (cierra) las puertas y llega (sale) a la estación (desde la estación) al instante y dnomomentno.

Progreso de la decisión

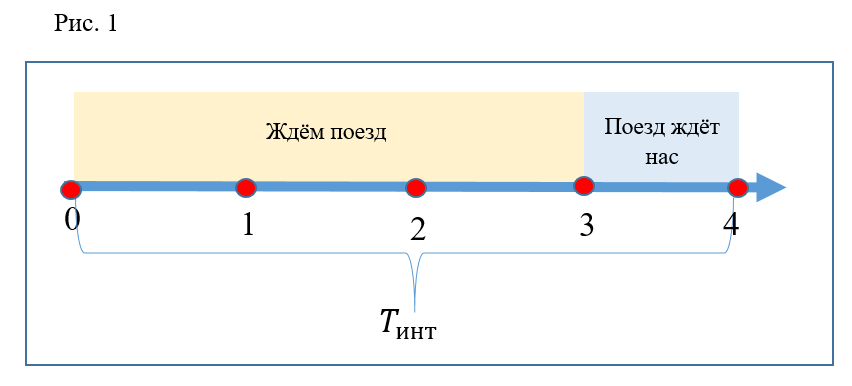
Dibujemos el eje del tiempo (Fig. 1). Todo el eje será intervalos consecutivos entre trenes. De aquí en adelante, solo se considerará un intervalo. Divida el intervalo que se muestra en 4 segmentos iguales. El punto 0 en este eje corresponde al momento en que el tren sale de la estación. El punto 3 corresponde a la llegada del tren y la apertura de las puertas. Punto 4: cierre de puertas y salida del tren. Por lo tanto, para la comodidad de la representación gráfica y los cálculos, el intervalo entre trenes se cuenta entre los momentos de salida de los trenes de la estación. Los primeros 3 segmentos son el tiempo que los pasajeros se ven obligados a esperar al tren que llega. El cuarto segmento es el tiempo de parada del tren, cuando los pasajeros pueden abordarlo. Pon también ese tiempo $$ (tiempo de descenso en la escalera mecánica) es igual a dos segmentos. Coeficiente $$ igual a 2, es decir, el tiempo de descenso corriendo 2 veces menos e igual a un segmento.



Ahora, para determinar la probabilidad $$ , descubra en qué período de tiempo la decisión de ir a correr conducirá al hecho de que el descenso será efectivo. Por ejemplo, si nuestros participantes se acercan a la escalera mecánica en el momento 0, entonces el primero estará en la plataforma en el momento $$ (Fig. 2), y la segunda anterior, por el momento $$ . Pero, como se puede ver en la figura, en ninguno de estos momentos hay un tren en la estación, lo que significa que correr era ineficiente.



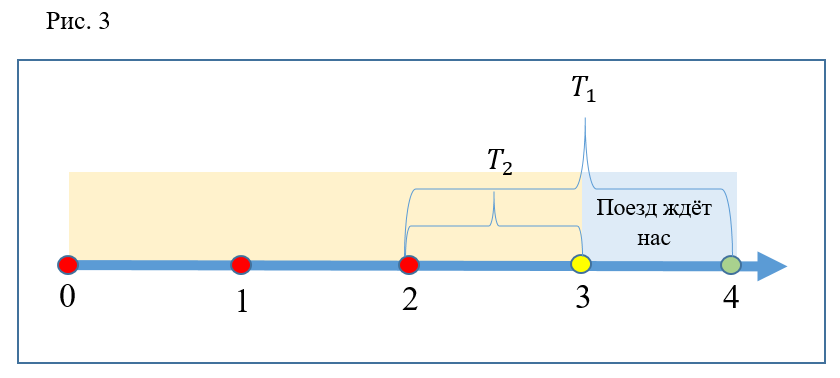
Considere otro caso (Fig. 3): los participantes en el experimento se acercan a la escalera mecánica en el momento 2. Como en el caso anterior, el primero estará en la plataforma en el momento $$ , y el segundo antes, por el momento $$ . Pero es obvio que en ambas ocasiones el tren está en la estación. Por lo tanto, ambos tendrán tiempo para abordar el mismo tren, por lo tanto, el agotamiento fue igual de ineficiente.



Además, es fácil entender que en cualquier momento en el intervalo de 2 a 3, es efectivo correr hacia abajo, ya que la persona escapada siempre se las arregla para abordar el tren, y no el que se escapó. Si elige puntos de tiempo entre 3 y 4, ambos participantes llegan tarde al tren y se ven obligados a esperar el siguiente juntos, es decir, volver a correr no es efectivo.

Resulta que, de los 4 períodos de tiempo convencionales, es eficaz reducir la velocidad solo si los participantes se acercan a la escalera mecánica entre 2 y 3 veces (Fig. 4). La probabilidad de entrar es 1/4. Por lo tanto, bajo las condiciones dadas de la tarea, no es práctico tomar una decisión de desvanecimiento, ya que el segundo participante tiene más probabilidades (con una probabilidad de 3/4) de correr en vano y se verá obligado a esperar el tren junto con el primero, que cayó más tarde.



Las siguientes observaciones serán completamente justas:

1. Los intervalos entre trenes pueden disminuir y aumentar. El tiempo de estacionamiento puede aumentar y el tiempo de espera puede disminuir (con el mismo intervalo) y viceversa.
2. La velocidad de la escalera mecánica hacia abajo es constante, pero el tiempo de descenso puede variar, ya que las estaciones pueden ser más o menos profundas.
3. El segundo participante puede correr no 2, sino 3 o incluso 4 veces más rápido que la escalera mecánica.

Para evaluar el impacto de los cambios en los factores anteriores, es necesario derivar la relación entre estos valores y la probabilidad de subirse a la escalera mecánica en un momento en que es eficaz disminuir.

Para hacer esto, describiremos otro caso (Fig. 5). Dejamos todos los datos originales sin cambios con la excepción de uno: coeficiente $$ aumentar a 4. Es decir, el segundo participante estará en la parte inferior 4 veces más rápido que el primero. Para la conveniencia de la imagen, dividimos nuestro intervalo en 8 partes iguales. Por lo tanto, el tiempo de descenso en la escalera mecánica ahora es igual a 4 segmentos, el tren se detiene en dos, el tiempo de espera es 6 y el tiempo de descenso para correr solo. No es difícil descubrir que ahora la duración del intervalo de tiempo "efectivo" (de 4 a 7 puntos en el tiempo) es 3. Es decir, la probabilidad $$ igual a 3/8. Esto ya es más que en el primer caso, pero no realizamos estos cambios para evaluar la probabilidad.



Basado en la Figura 4 y la Figura 5, es obvio que la longitud del segmento "efectivo" es $$ . Divídalo por la duración del intervalo y obtenga la probabilidad $$ donde $$ .
Realizamos una serie de transformaciones: $$$$ .
La fórmula final: $$ .

En base a esta fórmula, se pueden sacar varias conclusiones fundamentales a la vez:

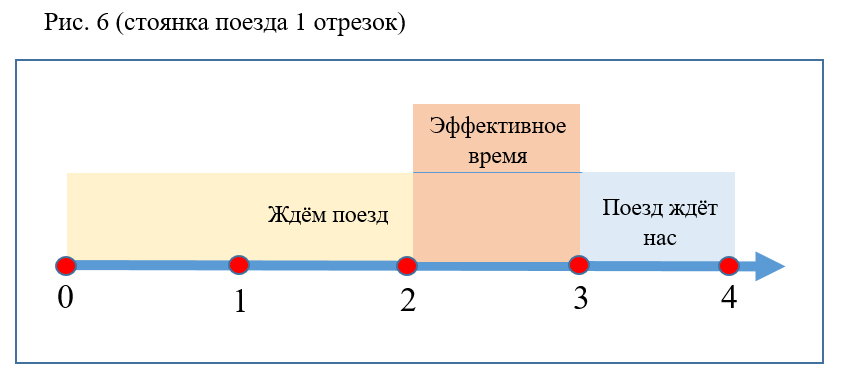
1. El valor de probabilidad no se ve afectado por los cambios en el tiempo de estacionamiento y el tiempo de espera del tren si el intervalo total no cambia (Fig. 6).
   
   
   
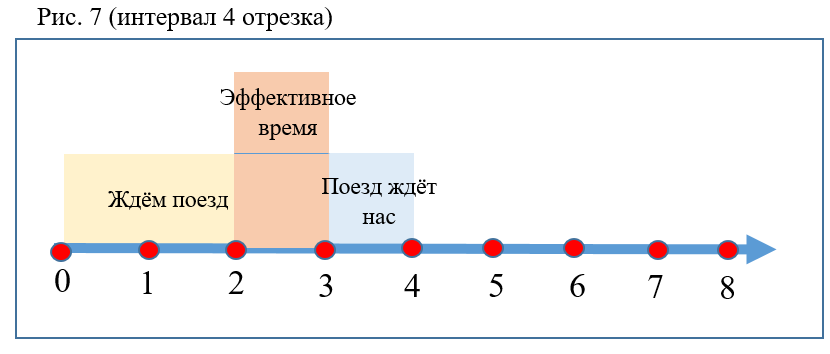
2. Cuanto mayor es el intervalo entre trenes, menor es la probabilidad P (Fig. 7).
   
   
   
3. La probabilidad aumenta si la relación del tiempo de descenso en la escalera mecánica al intervalo y / o el coeficiente K aumenta.
   

Cheque de fidelidad

Ahora veamos qué tan verdadera es la fórmula derivada.

Para verificar la exactitud de la fórmula, recurrimos a las estadísticas, que fueron muy útiles en 2014 por el corresponsal de The Village. Expreso mi reconocimiento y, naturalmente, al final del artículo dejaré un enlace al artículo original. También es bueno que las estadísticas se presenten como infografías visuales.

Experimento 1. Estación de metro Chekhovskaya



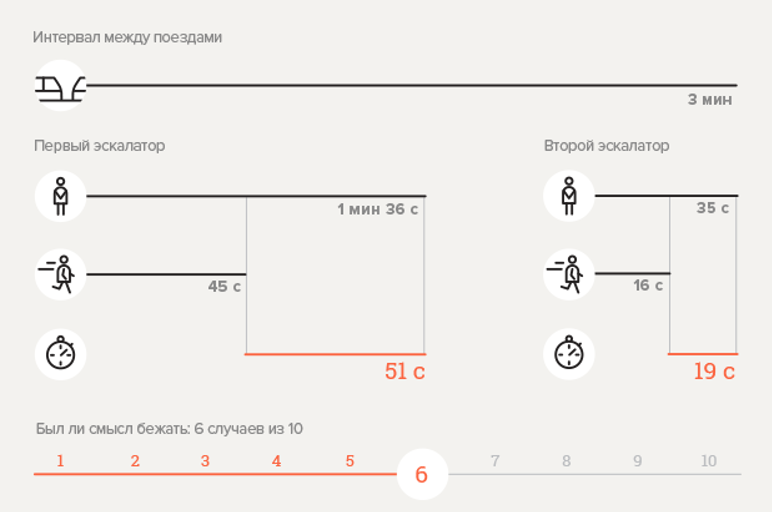
Calcular la probabilidad $$ .
Aqui $$ ; $$ ; $$ ; $$ ; $$ .

El resultado obtenido, aparentemente, difiere de los datos experimentales. ¿Está mal la fórmula? No! Se puede ver en la infografía que el descenso a la estación implica un viaje en dos escaleras mecánicas, sin embargo, el tiempo de transición entre ellas no se tiene en cuenta. Si, por confiabilidad, asumimos que la transición toma al menos 30 segundos, entonces, sustituyendo un nuevo valor $$ obtenemos: $$ ; $$ , que está mucho más cerca del resultado experimental. También vale la pena señalar que el experimento proporcionó solo 10 repeticiones. Al aumentar el número de repeticiones, es posible lograr una coincidencia casi completa de los datos calculados con los resultados obtenidos durante el experimento.

Experimento 2. Estación de metro "Parque de la Victoria"



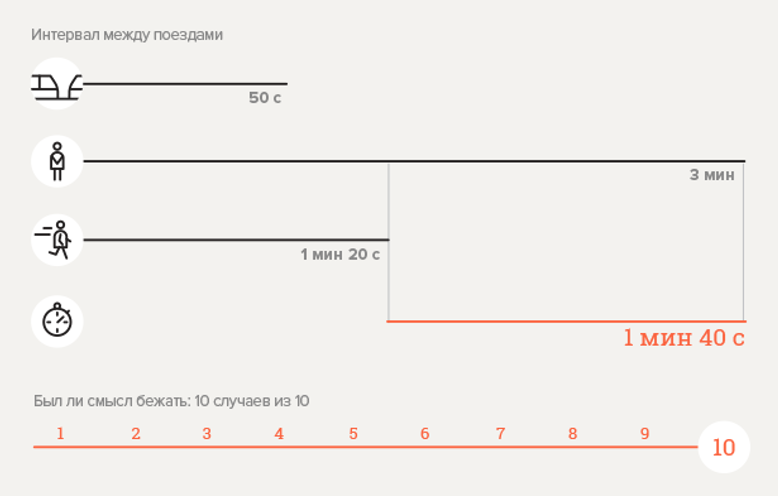
Calcular la probabilidad $$ .
Aqui $$ ; $$ ; $$ ; $$ ; $$ .
Se puede ver que tenemos una probabilidad mayor que uno. Pero no hay contradicción aquí. Si observa la forma general de la fórmula, resulta obvio que en el caso de que el tiempo de descenso en la escalera mecánica sea igual al intervalo entre trenes, un aumento de la velocidad de al menos 2 veces hará que la probabilidad de que el descenso acelerado sea efectivo igual a 0.5. Si el tiempo de viaje de la escalera mecánica es mayor que el intervalo, entonces con el mismo coeficiente $$ la probabilidad de tomar un tren antes solo aumentará. Finalmente, si el tiempo de descenso en la escalera mecánica es 2 o más veces el intervalo, la persona que corre en el 100% de los casos llegará a tiempo al tren para el que el resto de la escalera mecánica no tendrá tiempo. Es este efecto el que observamos en este experimento: el corresponsal concluyó que se lavó en 10 de cada 10 casos.

Experimento 3. Estación de metro Park Kultury



Calcular la probabilidad $$ .
Aqui $$ ; $$ ; $$ ; $$ ; $$ .

¿Otra vez un error? En absoluto Se puede ver que, como se indicó anteriormente, el tiempo de descenso en la escalera mecánica es 2 veces el intervalo entre trenes. El tiempo de ejecución es 2 veces menor. Resulta que cada descenso debería ser efectivo. Pero no olvide que antes de comenzar la discusión, asumimos el cierre instantáneo de las puertas y, al menos, la salida instantánea del tren de la estación. Si imagina una opción como la que se muestra en la Figura 8, queda claro que en la vida real una persona fugitiva puede no tener tiempo para sentarse en el punto 1 (por ejemplo, el tren partirá un poco antes) y en el punto 2, el tren, por el contrario, se retrasará un poco, y luego una persona que no corre se sentará en él junto con una persona que corre tarde en el tren anterior.



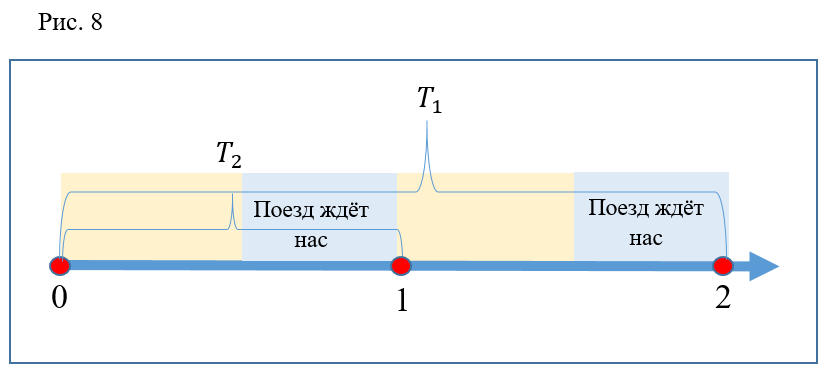
Supongo que en ambos tiempos "ineficaces" sucedió. Hay muchas razones para argumentar que con un aumento en el número de repeticiones del experimento, el porcentaje de ejecuciones "efectivas" tenderá al 100%.

Conclusiones

Ahora que, con base en los datos experimentales disponibles, fue posible confirmar la exactitud de la fórmula, la analizaremos y sacaremos conclusiones. Desde el principio, acordamos que consideraríamos la decisión de correr a la baja si la probabilidad de un descenso efectivo es mayor o igual a 0.5. Es decir, literalmente, si podemos estar seguros de que en al menos la mitad de los casos correremos por una buena razón, entonces realmente vale la pena correr el riesgo y correr, porque si llegamos tarde, prácticamente no perderemos nada. Con base en lo anterior, reescribimos la fórmula de probabilidad de la siguiente manera: $$ .

Es interesante que, como ya hemos descubierto, tiene sentido correr siempre cuando $$ . Al mismo tiempo, también es cierto que si $$ , no importa qué tan rápido corras, la probabilidad de subir a un tren antes es inferior a 0,5, ya que es obvio que $$ nunca será mayor o igual que 1.

Ahora echemos un vistazo a la velocidad del corresponsal. En promedio, es aproximadamente 2 veces la velocidad de la escalera mecánica (el tiempo de descenso es 2 veces menor). En general, estos datos coinciden con los resultados de mis propios experimentos (no veo el punto de traerlos). Como regla, ya es difícil desarrollar una velocidad con un coeficiente K de al menos 3: hay muchas personas que quieren correr escaleras abajo en una escalera mecánica real y, además, las personas paradas a su izquierda o sus cosas (bolsas, maletas) pueden interferir. Significa $$ y $$ . Es decir, una decisión de acelerar será apropiada solo si la relación $$ no menos de 1. Y esto es posible solo cuando el tiempo de descenso en la escalera mecánica no es menor que el intervalo entre trenes. En un metro real, donde el intervalo promedio entre trenes es de 2 minutos, no todas las estaciones pueden presumir de un largo descenso. Como regla general, incluso en el metro de San Petersburgo, el tiempo de viaje de la escalera mecánica es de aproximadamente 1 minuto y 30 segundos, es decir, 0,75 veces menos que el intervalo. De esto se desprende la conclusión fundamental muy obvia y más importante: si sabe con seguridad que la escalera mecánica en esta estación se mueve menos que el intervalo entre trenes, entonces no es práctico correr a lo largo de ella.

PD Tenga en cuenta el hecho de que esta tarea no tiene en cuenta la necesidad de subir a un carro específico. Se trata exclusivamente de subir a la plataforma y luego abordar el tren.

Fuente de datos experimentales: The Village . Gracias de nuevo!