El conjunto de datos utilizado a continuación se toma de una competencia de kaggle ya aprobada
de aquí .
En la pestaña Datos, puede leer la descripción de todos los campos.
Todo el código fuente
está en formato portátil
aquí .
Cargamos los datos, verificamos que generalmente tengamos:
import numpy as np import pandas as pd dataset = pd.read_csv('../input/ghouls-goblins-and-ghosts-boo/train.csv')
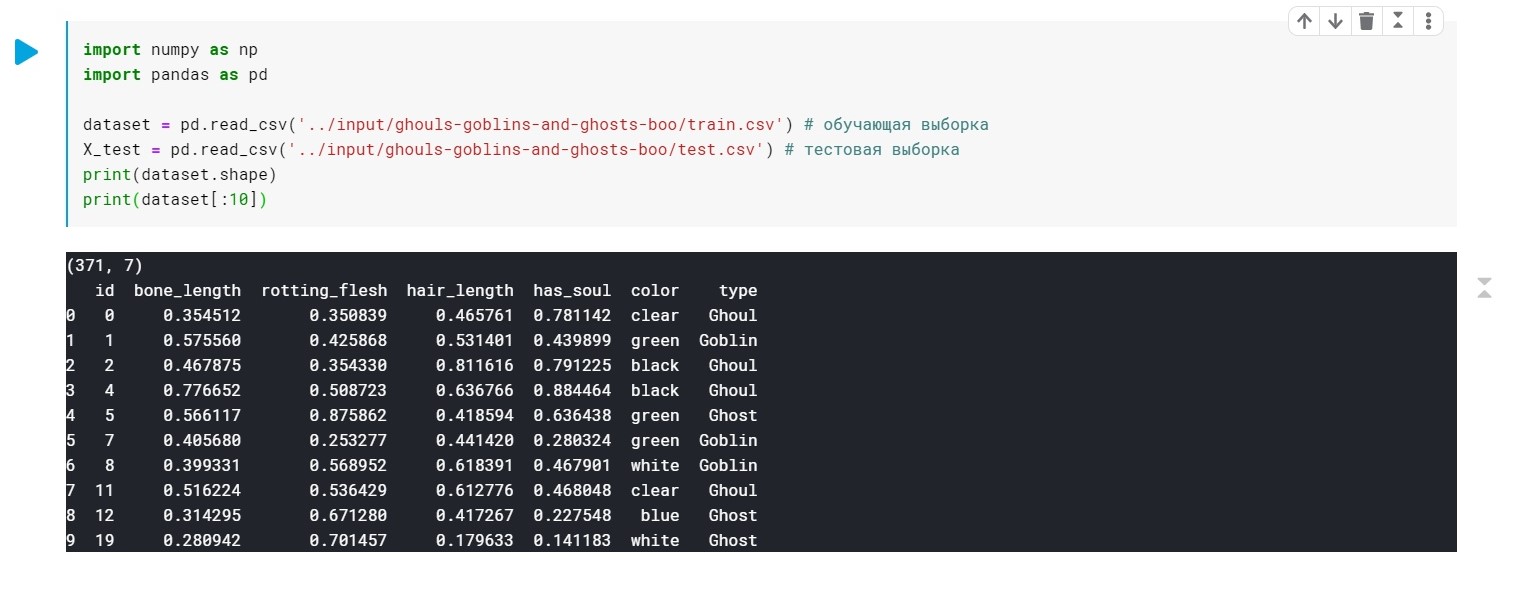
Los valores del campo de tipo (Ghoul, Ghost, Goblin) simplemente se reemplazan por 0, 1 y 2.
Color: también debe procesarse previamente (solo necesitamos valores numéricos para construir el modelo). Usaremos LabelEncoder y OneHotEncoder para esto.
Más detalles from sklearn.preprocessing import LabelEncoder, OneHotEncoder labelencoder_X_1 = LabelEncoder() X_train[:, 4] = labelencoder_X_1.fit_transform(X_train[:, 4]) labelencoder_X_2 = LabelEncoder() X_test[:, 4] = labelencoder_X_2.fit_transform(X_test[:, 4]) labelencoder_Y_2 = LabelEncoder() Y_train = labelencoder_Y_2.fit_transform(Y_train) one_hot_encoder = OneHotEncoder(categorical_features = [4]) X_train = one_hot_encoder.fit_transform(X_train).toarray() X_test = one_hot_encoder.fit_transform(X_test).toarray()
Bueno, en este punto nuestros datos están listos. Queda por entrenar a nuestro modelo.
Primero aplique
Adagrad :
En esencia, esta es una modificación del descenso de gradiente estocástico, sobre el cual escribí la última vez:
habr.com/en/post/472300Este método tiene en cuenta el historial de todos los gradientes pasados para cada parámetro individual (la idea de escalado). Esto le permite reducir el tamaño del paso de aprendizaje para los parámetros que tienen un gradiente grande:
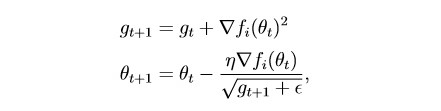
g es el parámetro de escala (g0 = 0)
θ - parámetro (peso)
epsilon es una pequeña constante introducida para evitar la división por cero
Divida el conjunto de datos en 2 partes:
Muestra de entrenamiento (tren) y validación (val):
from sklearn.model_selection import train_test_split x_train, x_val, y_train, y_val = train_test_split(X_train, Y_train, test_size = 0.2)
Un poco de preparación para el entrenamiento modelo:
import torch import numpy as np device = 'cuda' if torch.cuda.is_available() else 'cpu' def make_train_step(model, loss_fn, optimizer): def train_step(x, y): model.train() yhat = model(x) loss = loss_fn(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() return loss.item() return train_step
Modelo de auto entrenamiento:
from torch import optim, nn model = torch.nn.Sequential( nn.Linear(10, 270), nn.ReLU(), nn.Linear(270, 3)) lr = 0.01 n_epochs = 500 loss_fn = torch.nn.CrossEntropyLoss() optimizer = optim.Adagrad(model.parameters(), lr=lr) train_step = make_train_step(model, loss_fn, optimizer) from sklearn.utils import shuffle for epoch in range(n_epochs): x_train, y_train = shuffle(x_train, y_train)
Calificación del modelo:
Aquí, además de las capas, solo tenemos 2 parámetros configurables (por ahora):
tasa de aprendizaje y n_epochs (número de eras).
Dependiendo de cómo combinemos estos dos parámetros, pueden surgir 3 situaciones:
1 - todo está bien, es decir el modelo muestra baja pérdida en la muestra de entrenamiento y alta precisión en la validación.
2 - adaptación insuficiente: gran pérdida en la muestra de entrenamiento y baja precisión en la validación.
3 - sobreajuste - baja pérdida en la muestra de entrenamiento, pero baja precisión en la validación.
Con el primero, todo está claro :)
Con el segundo, también parece experimentar con la tasa de aprendizaje y las n_epochs.
¿Y qué hacer con el tercero? La respuesta es simple: ¡regularización!
Anteriormente, teníamos una función de pérdida de la forma:
L = MSE (Y, y) sin términos adicionales
La esencia de la regularización es precisamente que, agregando un término a la función objetivo, "afina" el gradiente si es demasiado grande. En otras palabras, imponemos una restricción a nuestra función objetivo.
Existen muchos métodos de regularización. Más sobre L1 y L2 - regularización:
craftappmobile.com/l1-vs-l2-regularization/#_L1_L2El método Adagrad implementa la regularización L2, ¡apliquémosla!
Primero, para mayor claridad, observamos los indicadores del modelo sin regularización:
lr = 0.01, n_epochs = 500:
pérdida = 0.44 ...
Precisión: 0,71
lr = 0.01, n_epochs = 1000:
pérdida = 0,41 ...
Precisión: 0,75
lr = 0.01, n_epochs = 2000:
pérdida = 0,39 ...
Precisión: 0,75
lr = 0.01, n_epochs = 3000:
pérdida = 0.367 ...
Precisión: 0,76
lr = 0.01, n_epochs = 4000:
pérdida = 0.355 ...
Precisión: 0,72
lr = 0.01, n_epochs = 10000:
pérdida = 0.285 ...
Exactitud: 0.69
Aquí puede ver que en 4k + eras: el modelo ya está sobreajustado. Ahora intentemos evitar esto:
Para hacer esto, agregue el parámetro weight_decay para nuestro método de optimización:
optimizer = optim.Adagrad(model.parameters(), lr=lr, weight_decay = 0.001)
Con lr = 0.01, m_epochs = 10000:
pérdida = 0.367 ...
Precisión: 0,73
A 4000 eras:
pérdida = 0.389 ...
Precisión: 0,75
Resultó mucho mejor, pero agregamos solo 1 parámetro en el optimizador :)
Ahora considere SGDm (este es un descenso de gradiente estocástico con una pequeña extensión, heurística, si lo desea).
La conclusión es que
SGD actualiza los parámetros con bastante fuerza después de cada iteración. Sería lógico "suavizar" el gradiente utilizando gradientes de iteraciones pasadas (la idea de la inercia):
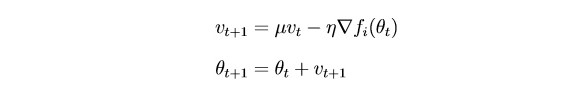
θ - parámetro (peso)
µ - hiperparámetro de inercia
SGD sin parámetro de impulso:
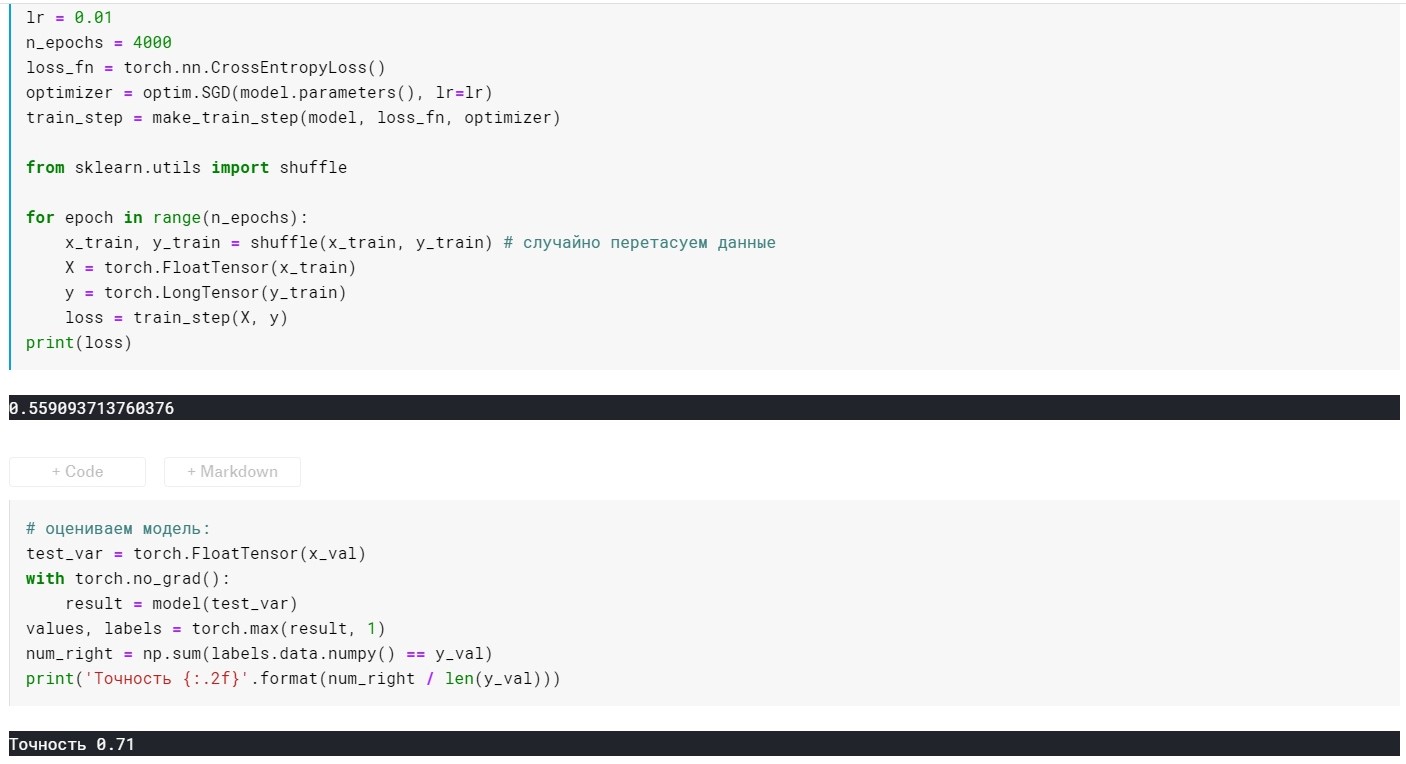
SGD con parámetro de impulso:
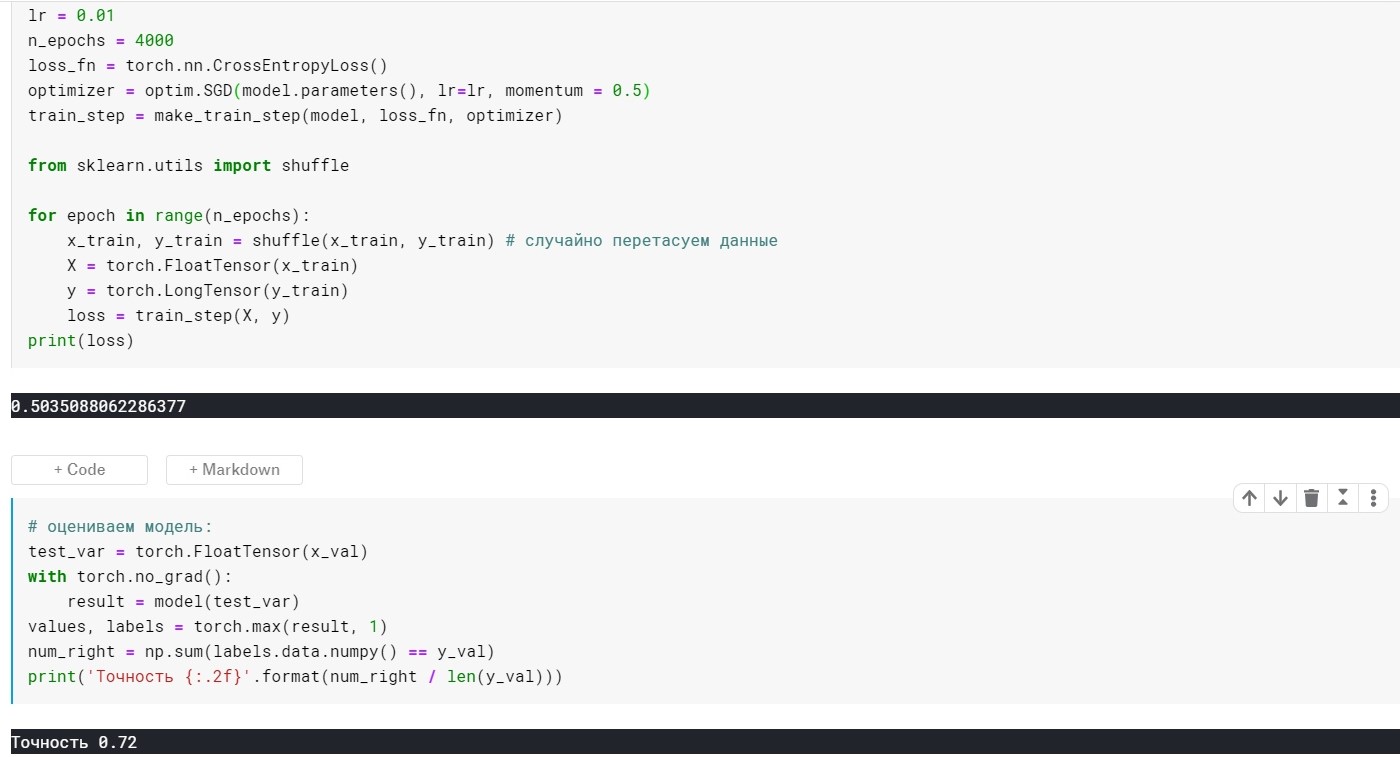
Resultó no mucho mejor, pero el punto aquí es que hay métodos que utilizan de inmediato las ideas de escala e inercia. Por ejemplo, Adam o Adadelta, que ahora muestran buenos resultados. Bueno, para comprender estos métodos, creo que es necesario comprender algunas ideas básicas utilizadas en métodos más simples.
¡Gracias a todos por su atención!