VK tiene un grupo con la siguiente descripción:

La misma foto se guarda manualmente todos los días en una computadora y se vuelve a cargar, perdiendo calidad gradualmente.

A la izquierda está la imagen original cargada el 7 de junio de 2012, a la derecha es lo que es ahora.

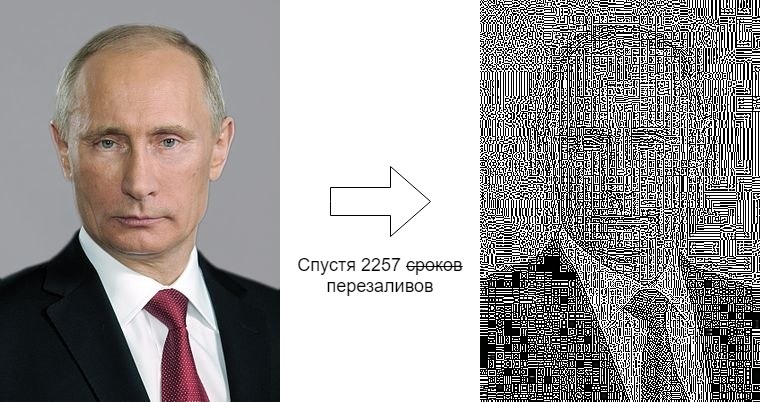
Esta diferencia es muy sospechosa. Tratemos de descubrir qué sucedió durante estos 7 años. Para conocerlo, hay un artículo sobre Medusa sobre este grupo, pero solo el lado técnico nos interesará.

Por qué y en qué etapa JPEG se comprime con pérdidas

Considere un esquema de codificación y decodificación JPEG altamente simplificado. Solo se muestran aquellas operaciones que ilustran los principios básicos del algoritmo JPEG.

Entonces, 4 operaciones:

• DCT es una transformada discreta del coseno.
• Cuantización: redondeando cada valor al múltiplo más cercano del paso de cuantización: y = [x / h] * h, donde h es el paso.
• IDCT es la transformada discreta inversa del coseno.
• El redondeo es un redondeo normal. Esta etapa no se pudo mostrar en el diagrama, ya que es obvio. Pero entonces se demostrará su importancia.

El color verde indica operaciones que guardan toda la información (sin tener en cuenta las pérdidas cuando se trabaja con números de coma flotante), las de color rosa: pierden. Es decir, las pérdidas y los artefactos aparecen no por la transformación del coseno, sino por la simple cuantización. El artículo no considerará una etapa importante: la codificación de Huffman, ya que se realiza sin pérdida.

Considere estos pasos con más detalle.

DCT

Como hay varias variaciones de DCT, por si acaso, aclararé que JPEG usa un segundo tipo de DCT con normalización. Al codificar, cada imagen se divide en cuadrados de 8x8 (para cada canal). Cada uno de esos cuadrados se puede representar como un vector de 64 dimensiones. La transformación del coseno es encontrar las coordenadas de este vector en otra base ortonormal. Es difícil visualizar el espacio de 64 dimensiones, por lo que a continuación se darán analogías bidimensionales. Puedes imaginar que la imagen se divide en bloques de 2x1. En los gráficos que se mostrarán a continuación, el eje x corresponde a los valores del primer píxel del bloque, el eje y al segundo.

Continuando con la analogía con un ejemplo específico, suponga que los valores de dos píxeles de la imagen original son 3 y 4. Dibuje el vector (3, 4) en la base original, como se muestra en la figura a continuación. La base original está marcada en azul. Las coordenadas del vector en alguna nueva base son (4.8, 1.4).

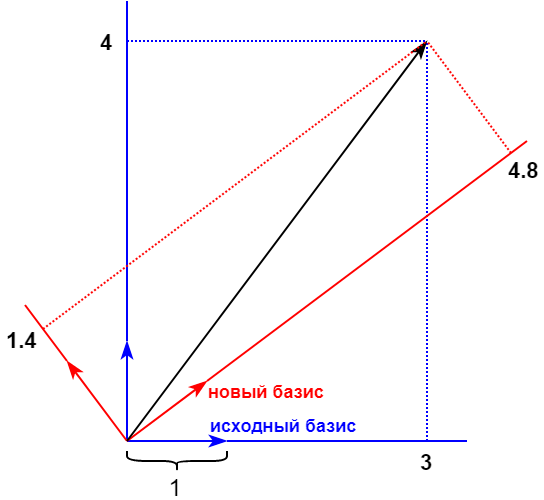
En el ejemplo considerado, se eligió una nueva base al azar. DCT ofrece una base fija de 64 dimensiones muy específica. La justificación de por qué se usa en JPEG es muy interesante y la describí en otro artículo . Solo tocaremos la esencia. En general, los valores de todos los píxeles son equivalentes. Pero si los convertimos usando DCT, entonces, a partir de las 64 coordenadas resultantes en una nueva base (llamados coeficientes de transformación DCT), podemos poner a cero de forma segura o redondear algunos de ellos, con pérdidas mínimas. Esto es posible gracias a las características de las imágenes comprimibles.

Cuantización

Los valores fraccionarios no se pueden guardar en un archivo. Por lo tanto, dependiendo del paso de cuantización, los valores 4.8, 1.4 se guardarán de la siguiente manera:

• en el paso 1 (la opción más suave): 5 y 1,
• en el paso 2: 4 y 2,
• en el paso 3: 6 y 0.

Por lo general, el paso se elige de manera diferente para cada valor. Un archivo JPEG tiene al menos una matriz, llamada tabla de cuantificación, que almacena 64 pasos de cuantización. Esta tabla depende de la calidad de compresión establecida en cualquier editor de gráficos.

IDCT

Igual que DCT, pero con una base transpuesta. Matemáticamente, x = IDCT (DCT (x)), por lo que si no hubiera cuantificación, entonces sería posible recuperarse sin pérdida. Pero no habría compresión. Debido al uso de la cuantización, el vector original no siempre se puede calcular con precisión. La siguiente figura muestra 2 ejemplos con recuperación precisa e inexacta. La cuadrícula inclinada corresponde a una nueva base, la línea recta a la original.

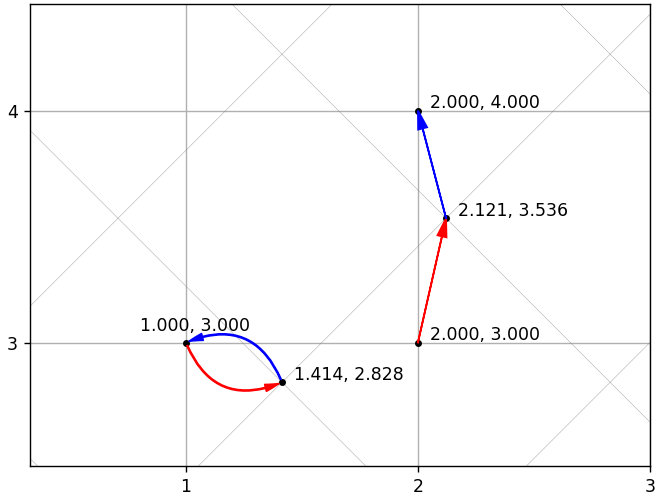
Surge la pregunta obvia: ¿puede una secuencia de transcodificación conducir a un vector que es muy diferente del original? Tal vez

Sería interesante clasificar todos los vectores enteros y ver a qué conducirá su transcodificación. Para reducir el ruido de la información, eliminamos la cuadrícula de la base inicial y conectaremos directamente los vectores originales y reconstruidos (sin un paso intermedio) por segmentos. Primero, considere un paso de cuantización igual a 1 para todas las coordenadas. La nueva base en la siguiente figura se rota 45 grados y para ello tenemos un 17,1% de recuperaciones inexactas. Los colores de los segmentos no significan nada, pero serán útiles para evitar su fusión visual.

Esta base es de 10.3 grados con recuperaciones inexactas del 7.4%:

Cerca de:

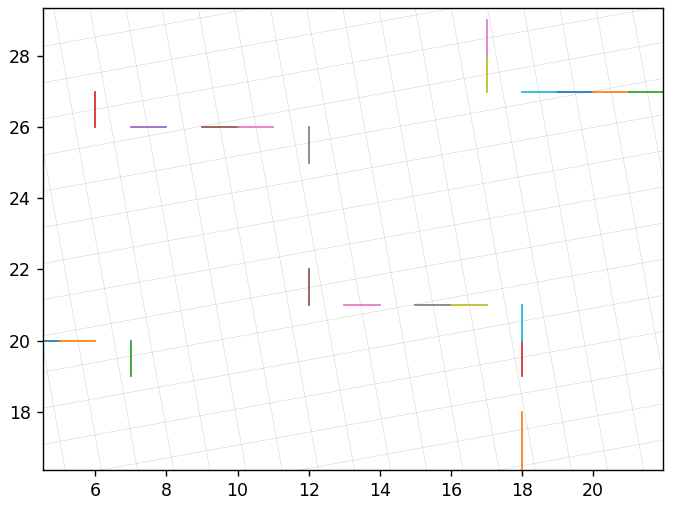
Y este está en 10.4 desde 6.4%:

19 grados desde 12.5%:

Pero si establece el paso de cuantificación mayor que 1, los vectores reconstruidos comienzan a concentrarse claramente cerca de los nodos de la cuadrícula. Este es el paso 5:

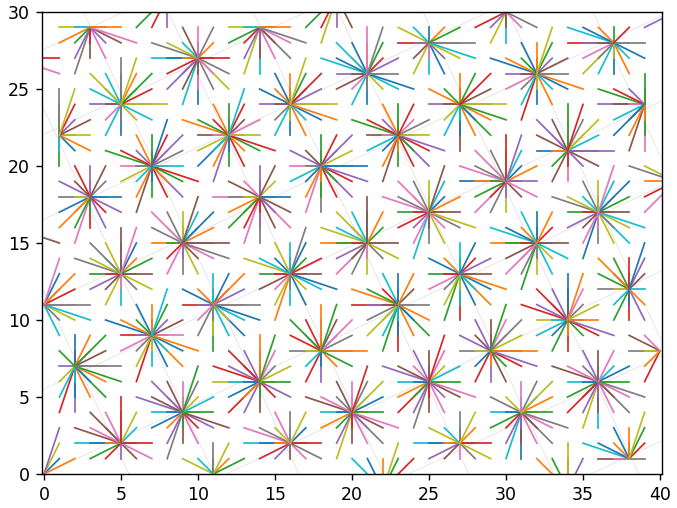
Esto es 2:

Si recodifica la imagen varias veces, pero con el mismo tono, casi nada sucederá en comparación con una sola grabación. Los valores parecen estar "atascados" en los nodos de la cuadrícula y ya no pueden "saltar" desde allí a otros nodos. Si el paso es diferente, entonces el vector "saltará" de un nodo de la cuadrícula a otro. Esto puede llevarlo a cualquier parte. La siguiente figura muestra el resultado de 4 transcodificaciones con los pasos 1, 2, 3, 4. Puede ver una cuadrícula grande con el paso 12. Este valor es el mínimo común múltiplo de 1, 2, 3, 4.

Y sobre esto, con los pasos del 1 al 7. La visualización se muestra solo para parte de los vectores originales para mejorar la visualización.

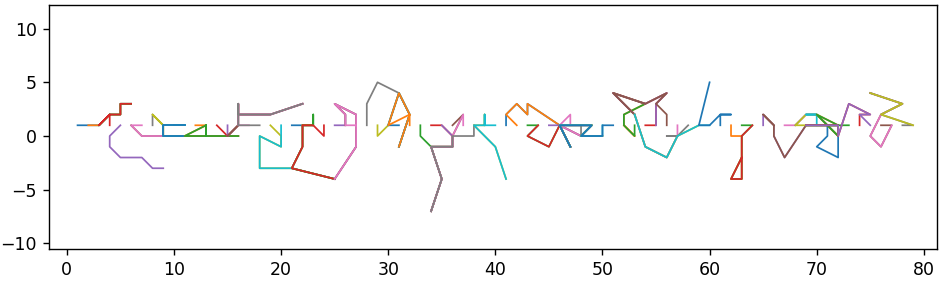
Redondeo

¿Por qué redondear los valores después de IDCT? Después de todo, si se deshace de esta etapa, la imagen restaurada estará representada por valores fraccionarios y no perderemos nada al volver a codificar. Desde un punto de vista matemático, simplemente nos moveremos de una base a otra sin pérdida. Es necesario mencionar aquí la conversión de espacios de color. Aunque JPEG no regula el espacio de color y le permite guardar directamente en la fuente RGB, pero en la gran mayoría de los casos, se utiliza la conversión preliminar a YCbCr. Características de los ojos y todo eso. Y tal conversión también conduce a pérdidas.

Supongamos que obtenemos un archivo JPEG comprimido con la máxima calidad, es decir, con un paso de cuantización de 1 para todos los coeficientes. No sabemos qué códec se usó, pero generalmente los códecs realizan el redondeo después de la conversión RGB -> YCbCr. Dado que la calidad es máxima, después de IDCT obtenemos valores fraccionarios, pero bastante cercanos a los originales en el espacio YCbCr. Si redondeamos, la mayoría de ellos se restaurarán exactamente.

Pero si no es redondo, entonces debido a diferencias tan pequeñas, la conversión YCbCr -> RGB puede incluso alejarlos aún más de los valores originales. Con la transcodificación posterior, la brecha aumentará más y más. Para visualizar de alguna manera este proceso, utilizamos el método del componente principal para proyectar vectores de 64 dimensiones en un plano. Luego, para 1000 transcodificaciones, obtenemos aproximadamente la siguiente secuencia de cambios:

Los valores absolutos de los ejes aquí no tienen mucho sentido, pero se puede usar la importancia relativa de las distorsiones.

Múltiples ejemplos de transcodificación

Gato de origen:

Después de una nueva preservación con calidad 50:

Después de cualquier número posterior de transcodificaciones con la misma calidad, la imagen no cambia. Ahora reduciremos gradualmente la calidad de 90 a 50 en 1:

Casi lo mismo sucedió en el cuadro a continuación:

Después de una nueva preservación con calidad 20:

Perfectamente de 90 a 20:

Ahora 1000 veces con calidad aleatoria de 80 a 90:

10,000 veces:

Análisis de imágenes del grupo VK

Comencemos el análisis de más de 2000 imágenes del grupo VK. Primero, verifique la desviación absoluta promedio de la primera. El eje x es el número de imagen (o día), el eje y es la desviación.

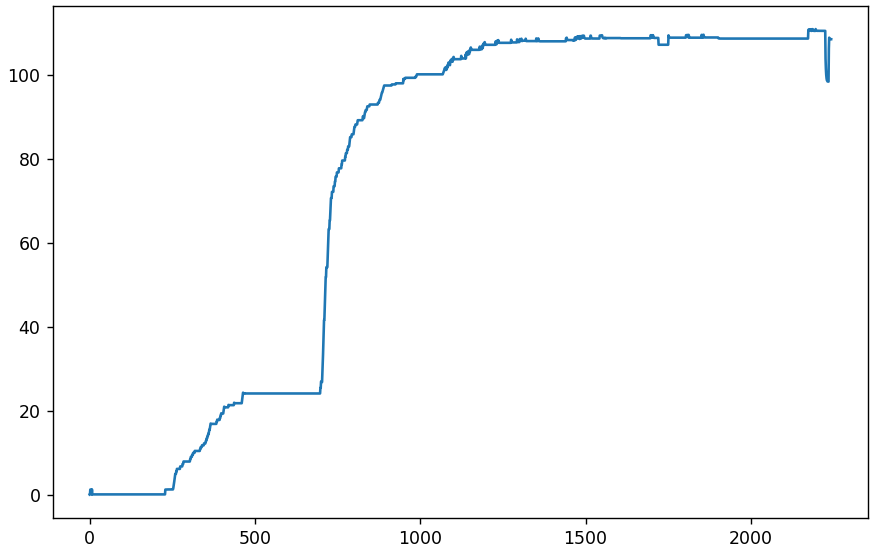
Pasemos al gráfico diferencial que muestra la desviación absoluta promedio de las imágenes vecinas.

Pequeñas fluctuaciones al principio son normales. Hasta el 232, todo va bien, las imágenes son completamente idénticas. Y el 233º repentinamente difiere en un promedio de 1.23 por cada píxel (en una escala de 0 a 255). Esto es mucho Tal vez las tablas de cuantificación acaban de cambiar. Compruébalo Y al mismo tiempo, es comparable con el tamaño de los archivos recibidos.

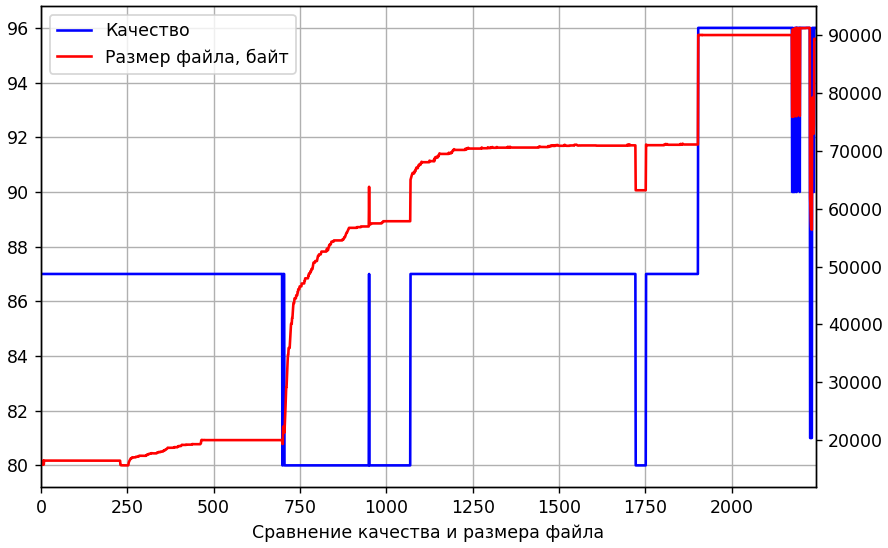
Sí, las mesas han cambiado. Pero no antes de los 700. Entonces, tal vez, ocurrió una transcodificación oculta intermedia con baja calidad. Intentemos volver a codificar el 232o dos veces. Por primera vez, pasaremos por diferentes niveles de calidad, y para el segundo usaremos la misma tabla de cuantificación que para todos, desde el primero hasta el 700. Nuestro objetivo es hacer que la imagen sea lo más similar posible a la 233a. En la siguiente figura, a lo largo del eje x está la calidad de la transcodificación intermedia, a lo largo de y es la desviación absoluta promedio del 233º.

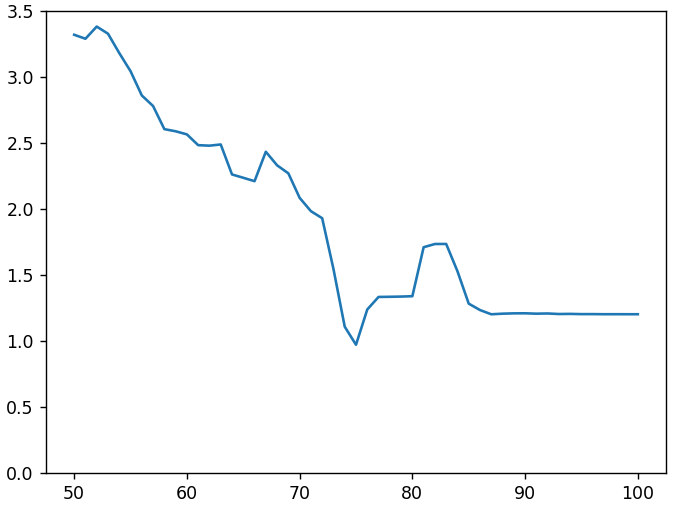
Aunque hay una falla en el gráfico con una calidad del 75%, aproximadamente igual a 1, pero aún lejos del cero deseado. Agregar la segunda etapa intermedia y cambiar los parámetros de submuestreo no mejoró la situación.

Con el resto de las imágenes, todo es casi igual, además el cambio en las tablas de cuantización también se superpone. Es decir, en algún momento, la imagen cambia dramáticamente, luego se estabiliza en unos pocos días, pero solo hasta que ocurre un nuevo aumento. Quizás haya un cambio en la imagen misma en los servidores. No puedo excluir completamente la participación del administrador del grupo.

Desafortunadamente, no descubrí lo que realmente sucedió con la imagen. Al menos ahora estoy seguro de que no fue solo una re-preservación. Pero, lo más importante, fue mejor representar los procesos en curso durante la codificación y decodificación. Espero que tú también.

Archivo con imágenes , para investigación independiente.