Splines en gráficos 3D, la opción más automatizada

Hace aproximadamente un mes, comencé a aprender Python del libro de Dawson y me desperté profundamente en el proceso de escribir mi juego en Pygame. TK fue tal que parecía más prometedor hacer un juego con gráficos pseudo-tridimensionales al rellenar las superficies guardadas de splines 3d en sprites. Escribiré sobre esto último.

Por lo tanto, hay polígonos (es más fácil trabajar con cuadrángulos) en los que queremos estirar las superficies cúbicas para que se unan con bastante suavidad: estas superficies son estrías.



Es más conveniente presentar una spline para un polígono como una función

$$

$$g (u, v) = v \ cdot g_1 (u) + (1 - v) \ cdot g_2 (u) + u \ cdot g_3 (v) + (1-u) \ cdot g_4 (v) (1) $$$

Aqui

$$

$$g_1, g_2, g_3, g_4$$

- polinomios cúbicos que satisfacen algunas condiciones de contorno (en la figura a continuación - curvas verde claro y rojo, y condiciones iniciales derivadas - vectores lila y azul); u y v varían de 0 a 1.



En esta interpretación, se pierden algunos grados (productos de 2 y 3 grados de parámetros), pero los coeficientes polinómicos se pueden encontrar especificando solo 12 vectores de condiciones iniciales (4 puntos poligonales y vectores derivados con respecto a u y v para cada punto). En las uniones, las splines coinciden si se establecen condiciones iniciales similares para los polígonos vecinos (los vectores derivados deben ser colineales, la superficie pasa a través de los mismos puntos del polígono).

Un problema, la derivada con tal declaración del problema en todo el borde puede no coincidir, habrá pequeños artefactos en las uniones. Puede pensar 4 condiciones más para corregir esto y agregar cuidadosamente otro término a la fórmula

$$

$$u \ cdot v \ cdot (u-1) \ cdot (v-1) \ cdot g_5 (u, v)$$

que no estropea las fronteras, pero este es un tema para un artículo separado.

Una alternativa es la superficie de Bezier , pero propone establecer 16 parámetros de significado matemático incomprensible (para mí), es decir. Se supone que el artista trabajará con sus propias manos. Esto no es muy adecuado para mí, por lo que sigue una bicicleta con muletas.

Los coeficientes (1) se calculan más fácilmente al encontrar la matriz inversa a la matriz de valores y derivados en las esquinas y multiplicar por las condiciones de entrada (tres veces, para cada coordenada). La matriz puede ser esta:


NumPy hace un excelente trabajo de esto.

Queda una pregunta: dónde obtener los vectores de derivados. Se supone que de alguna manera deben seleccionarse en función de la posición de los puntos vecinos (para el polígono) y por razones de suavidad.
Para mí personalmente, todavía era completamente contraintuitivo cómo lidiar con la longitud del vector derivado. La dirección es comprensible, pero ¿la longitud?

Como resultado, nació el siguiente algoritmo:

1. En la primera etapa, se produce una clasificación de puntos. En el gráfico (qué puntos de los polígonos y sus conexiones especifican), se buscan y almacenan ciclos de longitud 4 y, además, se registran los vecinos más adecuados para la función de extender los bordes del polígono (se determina de antemano qué bordes corresponden a un cambio en el parámetro u y cuáles corresponden a v). Aquí hay un fragmento de código que busca, clasifica y recuerda a los vecinos para el punto 0 de un ciclo:


Además, al construir la spline, la derivada a lo largo del borde (por ejemplo, con respecto al parámetro u) en el punto del polígono se selecciona en función de la ubicación de dos puntos del borde y un punto adyacente (sean los puntos vec1, vec2 y vec3; el punto en el que se busca la derivada es el segundo).



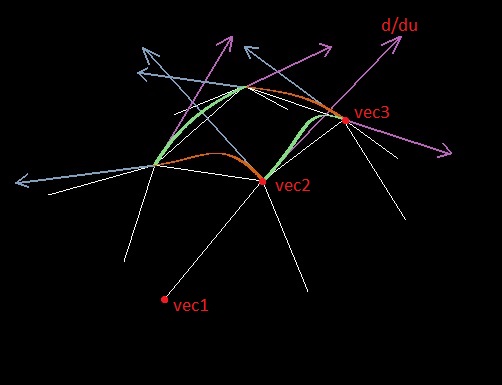
Al principio traté de usar el vector normalizado vec3 - vec1 (como apliqué el teorema de Lagrange) para este papel, pero surgieron problemas precisamente con la longitud del vector derivado; convertirlo en una constante fue una mala idea.

Digresión lírica:

Para una pequeña ilustración de cuál es el vector derivado en la versión paramétrica, recurrimos a una analogía bidimensional simple: aquí hay una pieza de un arco de círculo:

$$

$$g (u) = (Rsin (u \ pi / 2), Rcos (u \ pi / 2))$$

$$

$$g '(u) = (R \ pi / 2 \ cdot cos (u \ pi / 2), -R \ pi / 2 \ cdot sin (u \ pi / 2))$$

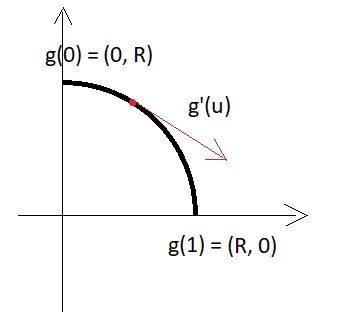
Es decir módulo derivativo = R * pi / 2 y, en términos generales, depende del tamaño de la pieza del arco, que establecemos a través del parámetro.

¿Qué hacer con eso ahora? Leo Nikolaevich Tolstoi nos legó que todo es redondo = bueno, por lo tanto, si establecemos la derivada en un punto como si quisiéramos construir un arco allí, obtendremos una curva suave y hermosa.

El final de la digresión.

La segunda etapa de la búsqueda derivada:

2. A través de nuestros tres puntos vec1, vec2, vec3 construimos un plano, en este plano buscamos un círculo que pase por los tres puntos. La derivada deseada se dirigirá a lo largo de la tangente al círculo en el punto vec2, y el módulo del vector de la derivada debe ser igual al producto del radio del círculo y el ángulo del sector, que forman dos puntos de la cara del polígono (similar a nuestra analogía plana simple de la digresión lírica).

$$

$$g '= R \ cdot \ phi$$

Todo parece ser simple, aquí está el código de función, por ejemplo (NumPy se usa nuevamente):


Bueno, en general, todo de alguna manera funciona. Para la demostración, tomé un cubo de 5x5x5 y cambié la posición de los puntos con un aleatorizador: