¿Por qué necesitamos rangos de C ++ 20 en una trituradora simple?

Recientemente, los rangos que deberían incluirse en el estándar C ++ 20 se han discutido bastante, incluso en Habré ( un ejemplo donde hay muchos ejemplos ). Hay suficientes críticos de intervalos, dicen que

• son demasiado abstractos y solo se necesitan para un código muy abstracto
• la legibilidad del código con ellos solo empeora
• intervalos ralentizan el código

Vamos a ver por completo trabajador-campesino tarea práctica, para comprender si esta crítica es válida y es cierto que Eric Nibler fue mordido por Bartosz Milewski y escribe range-v3 solo con la luna llena .

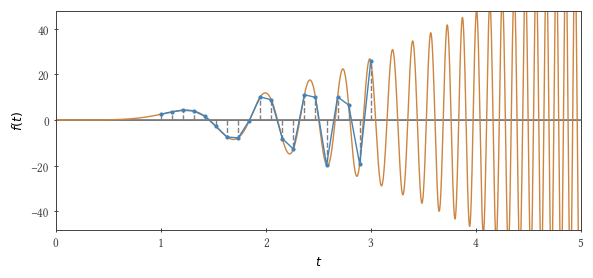
Integraremos la siguiente función utilizando el método trapezoidal:$$ $ en línea $ f (t) = 3 t ^ 2 \ sin t ^ 3 $ en línea $ que van desde cero a$$ $ en línea $ \ tau $ en línea $ . Si$$ $ en línea $ \ tau ^ 3 / \ pi $ en línea $ es igual a un número impar, entonces la integral es 2.

Entonces, el problema: escribimos un prototipo de una función que calcula la integral por el método trapezoidal . Parece, a primera vista, que no se necesitan abstracciones aquí, pero la velocidad es importante. De hecho, esto no es del todo cierto. Para el trabajo, a menudo tengo que escribir "trituradoras de números", cuyo usuario principal soy yo. Así que también tengo que apoyar y lidiar con sus errores (desafortunadamente mis colegas, no siempre solo yo). Y también sucede que parte del código no se usa, por ejemplo, un año, y luego ... En general, también es necesario escribir documentación y pruebas.

¿Qué argumentos debe tener una función integradora? Función y cuadrícula integrables (conjunto de puntos$$ $ en línea $ t_1, t_2, t_3 ... $ en línea $ usado para calcular la integral). Y si todo está claro con la función integrada ( std::function estará justo aquí), entonces ¿en qué forma se debe transmitir la grilla? A ver

Opciones

Para empezar, para que haya algo con lo que comparar el rendimiento, escribiremos un bucle simple con un paso de tiempo constante:

 // trapezoidal rule of integration with fixed time step; // dt_fixed is the timestep; n_fixed is the number of steps double integrate() { double acc = 0; for(long long i = 1; i < n_fixed - 1; ++i) { double t = dt_fixed * static_cast<double>(i); acc += dt_fixed * f(t); } acc += 0.5 * dt_fixed * f(0); acc += 0.5 * dt_fixed * f(tau); return acc; } 

Al usar este ciclo, puede pasar como argumentos a la función el principio y el final del intervalo de integración, así como el número de puntos para esta integración en sí. Detener: ¡el método trapezoidal también ocurre con un paso variable, y nuestra función integrable simplemente pide usar un paso variable! Que así sea, tengamos un parámetro más ($$ $ en línea $ b $ en línea $ ) para controlar la "no linealidad" y dejar que nuestros pasos sean, por ejemplo, los siguientes:$$ $ en línea $ \ Delta t (t) = \ Delta t_0 + bt $ en línea $ . Este enfoque (introducir un parámetro numérico adicional) probablemente se usa en un millón de lugares, aunque, al parecer, su defecto debería ser obvio para todos. ¿Y si tenemos una función diferente? ¿Y si necesitamos un pequeño paso en algún lugar en el medio de nuestro intervalo numérico? Pero, ¿qué pasa si una función integrable tiene un par de características? En general, debemos poder transmitir cualquier grilla. (Sin embargo, en los ejemplos, hasta el final, nos "olvidaremos" del método trapezoidal real y, por simplicidad, consideraremos su versión con un paso constante, teniendo en cuenta que la cuadrícula puede ser arbitraria).

Dado que la cuadrícula puede ser cualquiera, pasemos sus valores$$ $ en línea $ t_1, t_2, ... $ en línea $ envuelto en std::vector .

 // trapezoidal rule of integration with fixed time step double integrate(vector<double> t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } 

Hay más que suficientes comunidades en este enfoque, pero ¿qué pasa con el rendimiento? Con consumo de memoria? Si antes todo se resumía en el procesador, ahora primero tenemos que completar el área de memoria y luego leerlo. Y la comunicación con la memoria es algo bastante lento. Y el recuerdo aún no es de goma ( y silicona )

Veamos la raíz del problema. ¿Qué necesita una persona para ser feliz? Más precisamente, ¿qué necesita nuestro ciclo (basado en rango para bucle)? Cualquier contenedor con iteradores begin() y end() , y ++ , * y != Operadores para iteradores. Entonces escribiremos.

 //   ,    ,      template <typename T> double integrate(T t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } // ... //      class lazy_container { public: long long int n_nodes; lazy_container() { n_nodes = n_fixed; } ~lazy_container() {} class iterator { public: long long int i; // index of the current node iterator() { i = 0; } ~iterator() {} iterator& operator++() { i+= 1; return *this; } // ! bool operator!=(const iterator& rhs) const { return i != rhs.i; } double operator* () const { return dt_fixed * static_cast<double>(i); } }; iterator begin() { return iterator(); } iterator end() { iterator it; it.i = n_nodes; return it; } }; // ... //      lazy_container t_nodes; double res = integrate(t_nodes); 

Estamos calculando un nuevo valor aquí.$$ $ en línea $ t_i $ en línea $ a pedido, tal como lo hicimos en un bucle simple. No hay accesos a la memoria, y se espera que los compiladores modernos simplifiquen el código de manera muy eficiente. Al mismo tiempo, el código de la función integradora no ha cambiado mucho y aún puede digerir std::vector .

¿Dónde está la flexibilidad? De hecho, ahora podemos escribir cualquier función en el operador ++ . Es decir, este enfoque permite, de hecho, transferir una función en lugar de un único parámetro numérico. La cuadrícula generada sobre la marcha puede ser cualquiera, y también (probablemente) no perdemos rendimiento. Sin embargo, escribir un nuevo lazy_container cada vez para distorsionar de alguna manera la cuadrícula de una manera nueva no se siente en absoluto (¡son las mismas 27 líneas!). Por supuesto, puede hacer que la función responsable de generar la cuadrícula sea un parámetro de nuestra función integradora, y lazy_container también, es decir, discúlpeme, encapsúlelo.

Usted pregunta, ¿entonces algo volverá a estar mal? Si! En primer lugar, será necesario transmitir por separado el número de puntos para la integración, lo que puede causar un error. En segundo lugar, la bicicleta no estándar creada tendrá que ser apoyada y posiblemente desarrollada por alguien. Por ejemplo, ¿puede imaginar de inmediato cómo, con este enfoque, componer un combinador para funciones en el operador ++ ?

C ++ por más de 30 años. Muchos a esta edad ya tienen hijos, y C ++ ni siquiera tiene contenedores / iteradores perezosos estándar. Una pesadilla! Pero todo (en el sentido de los iteradores, no los niños) cambiará tan pronto como el próximo año: el estándar (posiblemente parcialmente) incluirá la biblioteca range-v3 , que ha sido desarrollada por Eric Nibler durante varios años. Utilizaremos las obras de sus frutos. El código lo dice todo por sí mismo:

 #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... auto t_nodes = ranges::v3::iota_view(0, n_fixed) | ranges::v3::views::transform( [](long long i){ return dt_fixed * static_cast<double>(i); } ); double res = integrate(t_nodes); 

La función integradora sigue siendo la misma. Es decir, ¡solo 3 líneas para resolver nuestro problema! Aquí iota_view(0, n) genera un intervalo iota_view(0, n) rango, un objeto que encapsula el inicio y el final generalizados; un intervalo diferido es una vista), que, al iterar en cada paso, calcula el siguiente número en el intervalo [0, n). Es curioso que el nombre ι (la letra griega iota) se refiera hace 50 años al lenguaje APL. Palo | le permite escribir tuberías de modificadores de intervalo y transform , de hecho, es un modificador que, utilizando una función lambda simple, convierte una secuencia de enteros en una serie$$ $ en línea $ t_1, t_2, ... $ en línea $ . Todo es simple, como en un cuento de hadas Haskell

¿Pero cómo hacer un paso variable? Todo es igual de simple:

 #include <range/v3/view/drop.hpp> #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... // trapezoidal rule of integration; step size is not fixed template <typename T> double integrate(T t_nodes) { double acc = 0; double t_prev = *(t_nodes.begin()); double f_prev = f(t_prev); for (auto t: t_nodes | ranges::v3::views::drop(1)) { double f_curr = f(t); acc += 0.5 * (t - t_prev) * (f_curr + f_prev); t_prev = t; f_prev = f_curr; } return acc; } //... auto step_f = [](long long i) { if (static_cast<double>(i) <= 1 / a) { return pow(2 * M_PI, 1/3.0) * a * static_cast<double>(i); } else { return tau * pow(static_cast<double>(i) / static_cast<double>(n), 1/3.0); } }; auto t_nodes = ranges::v3::iota_view(0, n) | ranges::v3::views::transform(step_f); double res = integrate(t_nodes); 

Un lector atento notó que en nuestro ejemplo, el paso variable nos permitió reducir el número de puntos de la cuadrícula en un factor de tres, mientras que adicionalmente, hay gastos notables para calcular$$ $ en línea $ t_i $ en línea $ . Pero si tomamos otro$$ $ en línea $ f (t) $ en línea $ , el número de puntos puede cambiar mucho más ... (pero aquí el autor ya se está volviendo vago).

Entonces los tiempos

Tenemos las siguientes opciones:

• v1 - bucle simple
• v2 -$$ $ en línea $ t_i $ en línea $ mentir en std::vector
• v3 - improvisado lazy_container con iterador improvisado
• v4 - intervalos de C ++ 20 (rangos)
• v5: rangos de nuevo, pero solo aquí el método trapezoidal se escribe usando un tono variable

Esto es lo que resulta (en segundos) para$$ $ inline $ \ tau = (10 \, 000 \, 001 \ times \ pi) ^ {1/3} $ inline $ , para g ++ 8.3.0 y clang ++ 8.0.0 en Intel® Xeon® CPU® X5550 (número de pasos sobre$$ $ en línea $ 1.5 \ veces 10 ^ 8 $ en línea $ , excepto para v5, donde los pasos son tres veces menos (el resultado de los cálculos de todos los métodos difiere de los dos en no más de 0.07):

En general, la mosca cruzó el campo, ¡la mosca encontró una moneda!

Resumen

Incluso en una tarea muy simple, los rangos resultaron ser muy útiles: en lugar de código con iteradores hechos a sí mismos en más de 20 líneas, escribimos 3 líneas, sin tener problemas con la legibilidad del código o su rendimiento.

Por supuesto, si necesitáramos (para) el máximo rendimiento en estas pruebas, tendríamos que aprovechar al máximo el procesador y la memoria escribiendo código paralelo (o escribiendo una versión en OpenCL) ... Además, no tengo idea de lo que sucederá si escribo cadenas muy largas de modificadores. ¿Es fácil depurar y leer los mensajes del compilador cuando se usan rangos en proyectos complejos? Aumentará el tiempo de compilación. Espero que alguien escriba sobre este artículo.

Cuando escribí estas pruebas, yo mismo no sabía qué pasaría. Ahora lo sé: los rangos definitivamente merecen ser probados en un proyecto real, en las condiciones en las que tiene la intención de usarlos.

Fui al bazar a comprar un samovar.

Enlaces utiles

rango-v3 inicio

Documentación y estudios de caso v3

código de este artículo en github

listas en Haskell, para comparar

Agradecimientos

¡Gracias Fadey por ayudar a escribir todo esto!

PS

Espero que alguien comente sobre tales rarezas: i) Si toma el intervalo de integración 10 veces más pequeño, en mi Xeon el ejemplo v2 es 10% más rápido que v1, y v4 es tres veces más rápido que v1. ii) El compilador Intel (icc 2019) a veces en estos ejemplos crea un código que es dos veces más rápido que el compilado g ++. ¿Es la vectorización la culpable? ¿Se puede obligar a g ++ a hacer lo mismo?