Introducción a las dependencias funcionales

En este artículo hablaremos sobre las dependencias funcionales en las bases de datos: qué es, dónde se aplica y qué algoritmos existen para su búsqueda.

Consideraremos las dependencias funcionales en el contexto de las bases de datos relacionales. Hablando muy groseramente, en tales bases de datos la información se almacena en forma de tablas. Además, utilizamos conceptos aproximados, que en una teoría relacional estricta no son intercambiables: llamaremos a la tabla en sí misma una relación, columnas - atributos (su conjunto es un diagrama de relación), y un conjunto de valores de fila en un subconjunto de atributos - una tupla.



Por ejemplo, en la tabla anterior, (Benson, M, M organ ) es una tupla de atributos (paciente, género, médico) .
Más formalmente, esto se escribe de la siguiente manera: $$$t_ {1}$[ Paciente, Paul, Doctor ] = (Benson, M, M órgano) .
Ahora podemos introducir el concepto de dependencia funcional (FZ):

Definición 1. La relación R satisface la ley federal X → Y (donde X, Y ⊆ R) si y solo para cualquier tupla $$$t_ {1}$, $$$t_ {2}$Holds R tiene: si $$$t_ {1}$[X] = $$$t_ {2}$[X] entonces $$$t_ {1}$[Y] = $$$t_ {2}$[Y] En este caso, se dice que X (un conjunto de atributos determinante o definitorio) define funcionalmente Y (un conjunto dependiente).

En otras palabras, la presencia de la Ley Federal X → Y significa que si tenemos dos tuplas en R y coinciden en los atributos de X , entonces también coincidirán en los atributos de Y.
Y ahora en orden. Considere los atributos de Paciente y Género para los que queremos saber si hay dependencias entre ellos o no. Para tantos atributos, pueden existir las siguientes dependencias:

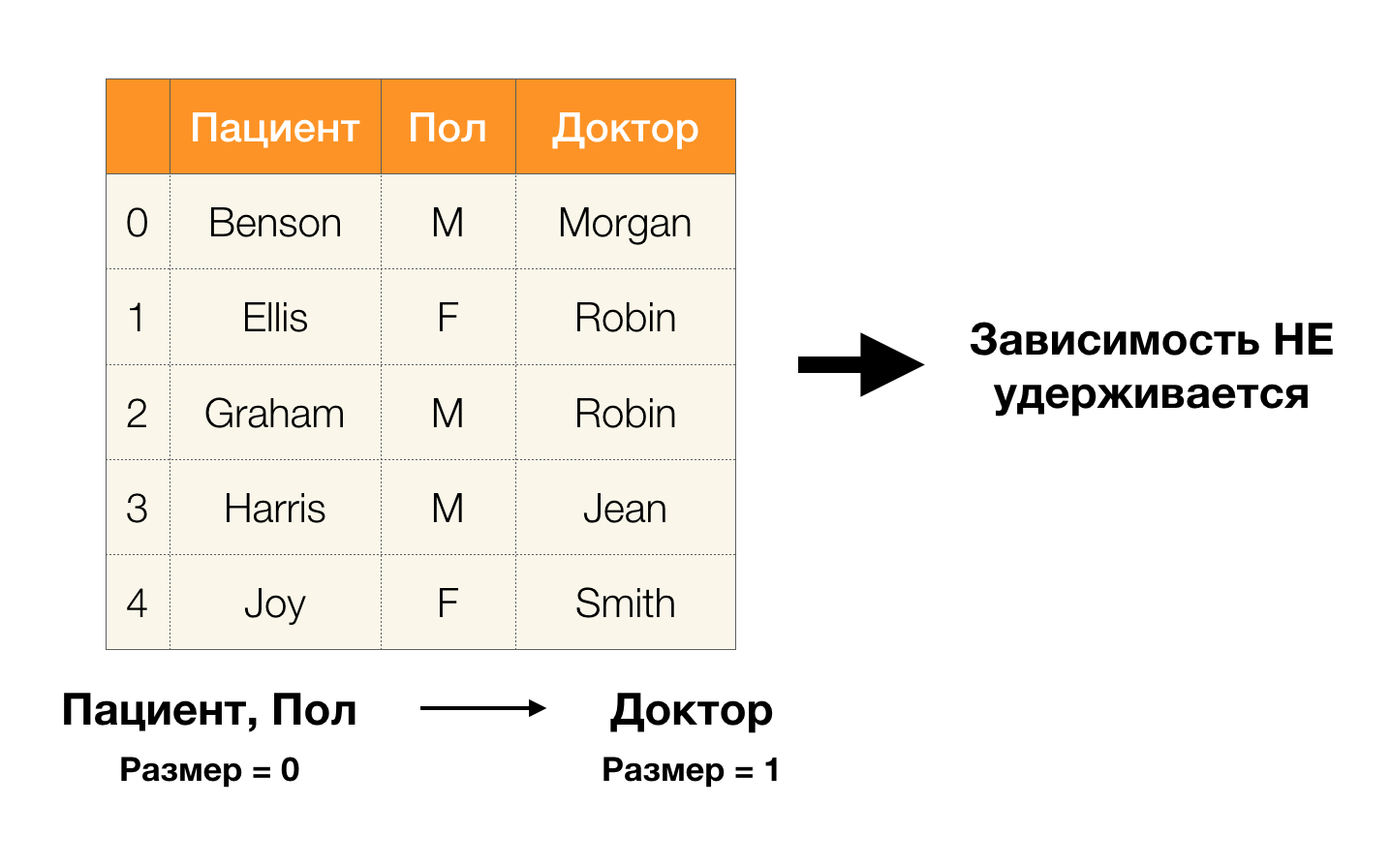
1. Paciente → Género
2. Género → Paciente

De acuerdo con la definición anterior, para mantener la primera dependencia, solo un valor de la columna Sexo debe corresponder a cada valor único de la columna Paciente . Y para la tabla de muestra, esto es cierto. Sin embargo, esto no funciona en la dirección opuesta, es decir, la segunda dependencia no se cumple, y el atributo de Paul no es un determinante para el paciente . Del mismo modo, si toma la dependencia Doctor → Paciente , puede ver que se viola, ya que el valor de Robin para este atributo tiene varios valores diferentes: Ellis y Graham .

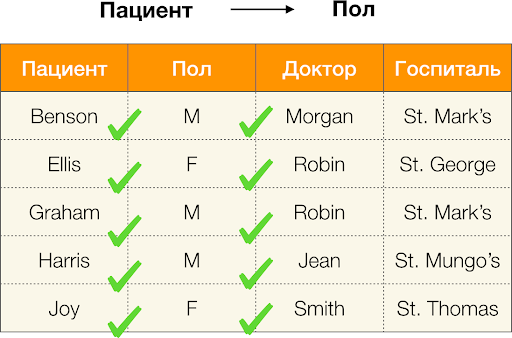
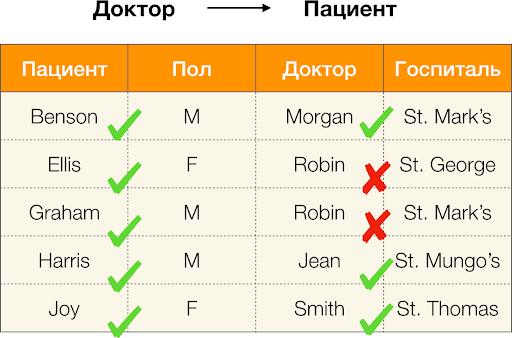
Por lo tanto, las dependencias funcionales hacen posible determinar las relaciones existentes entre los conjuntos de atributos de la tabla. De ahora en adelante, consideraremos las relaciones más interesantes, o más bien X → Y, de modo que sean:

• no trivial, es decir, el lado derecho de la dependencia no es un subconjunto de la izquierda (Y ̸⊆ X) ;
• mínimo, es decir, no existe tal dependencia Z → Y tal que Z ⊂ X.

Las dependencias consideradas hasta este punto eran estrictas, es decir, no incluían ninguna violación en la tabla, pero además de ellas, también existen aquellas que permiten cierta inconsistencia entre los valores de las tuplas. Dichas dependencias se colocan en una clase separada, llamada aproximada, y se permite violarlas en un cierto número de tuplas. Esta cantidad está regulada por el indicador de error emax máximo. Por ejemplo, la proporción de error $$$e_ {max}$= 0.01 puede significar que la dependencia puede ser violada por el 1% de las tuplas disponibles en el conjunto de atributos considerado. Es decir, para 1000 registros, un máximo de 10 tuplas puede violar la Ley Federal. Consideraremos una métrica ligeramente diferente basada en valores diferentes por pares de las tuplas comparadas. Para la dependencia X → Y de la relación r, se considera como sigue:

$$

$$e (X \ rightarrow Y, r) = \ frac {| \ {(t_1, t_2) \ in r ^ 2 \ | \ t_1 [X] = t_2 [X] \ wedge t_1 [Y] \ neq t_2 [Y] \} |} {| r ^ 2 | - | r |}$$

Calculamos el error para Doctor → Paciente a partir del ejemplo anterior. Tenemos dos tuplas, cuyos valores difieren en el atributo Paciente , pero coinciden en el Doctor : $$$t_ {1}$[ Doctor, paciente ] = ( Robin, Ellis ) y $$$t_ {2}$[ Doctor, paciente ] = ( Robin, Graham ). Siguiendo la definición de error, debemos tener en cuenta todos los pares en conflicto, lo que significa que habrá dos de ellos: ( $$$t_ {1}$, $$$t_ {2}$) y su inversión ( $$$t_ {2}$, $$$t_ {1}$) Sustituya en la fórmula y obtenga:

$$

$$\ frac {2} {5 ^ 2 - 5} = 0.1$$

Ahora tratemos de responder la pregunta: "¿Por qué es todo?". De hecho, las leyes federales son diferentes. El primer tipo son las dependencias determinadas por el administrador en la etapa de diseño de la base de datos. Por lo general, son pocos, son estrictos y la aplicación principal es la normalización de datos y el diseño del esquema de relación.

El segundo tipo son las dependencias que representan datos "ocultos" y relaciones previamente desconocidas entre atributos. Es decir, tales dependencias no se pensaron en el momento del diseño y ya se encuentran para el conjunto de datos existente, de modo que, en base al conjunto de leyes federales identificadas, saquen conclusiones sobre la información almacenada. Es con tales dependencias que estamos trabajando. Están involucrados en un área completa de datos de minería con diversas técnicas de búsqueda y algoritmos construidos sobre su base. Comprendamos cómo las dependencias funcionales encontradas (exactas o aproximadas) en cualquier dato pueden ser útiles.



Hoy, la limpieza de datos se encuentra entre las principales áreas de uso de la dependencia. Implica el desarrollo de procesos para identificar "datos sucios" con su posterior corrección. Los representantes brillantes de "datos sucios" son duplicados, errores de datos o errores tipográficos, valores faltantes, datos obsoletos, espacios adicionales y similares.

Error de datos de ejemplo:



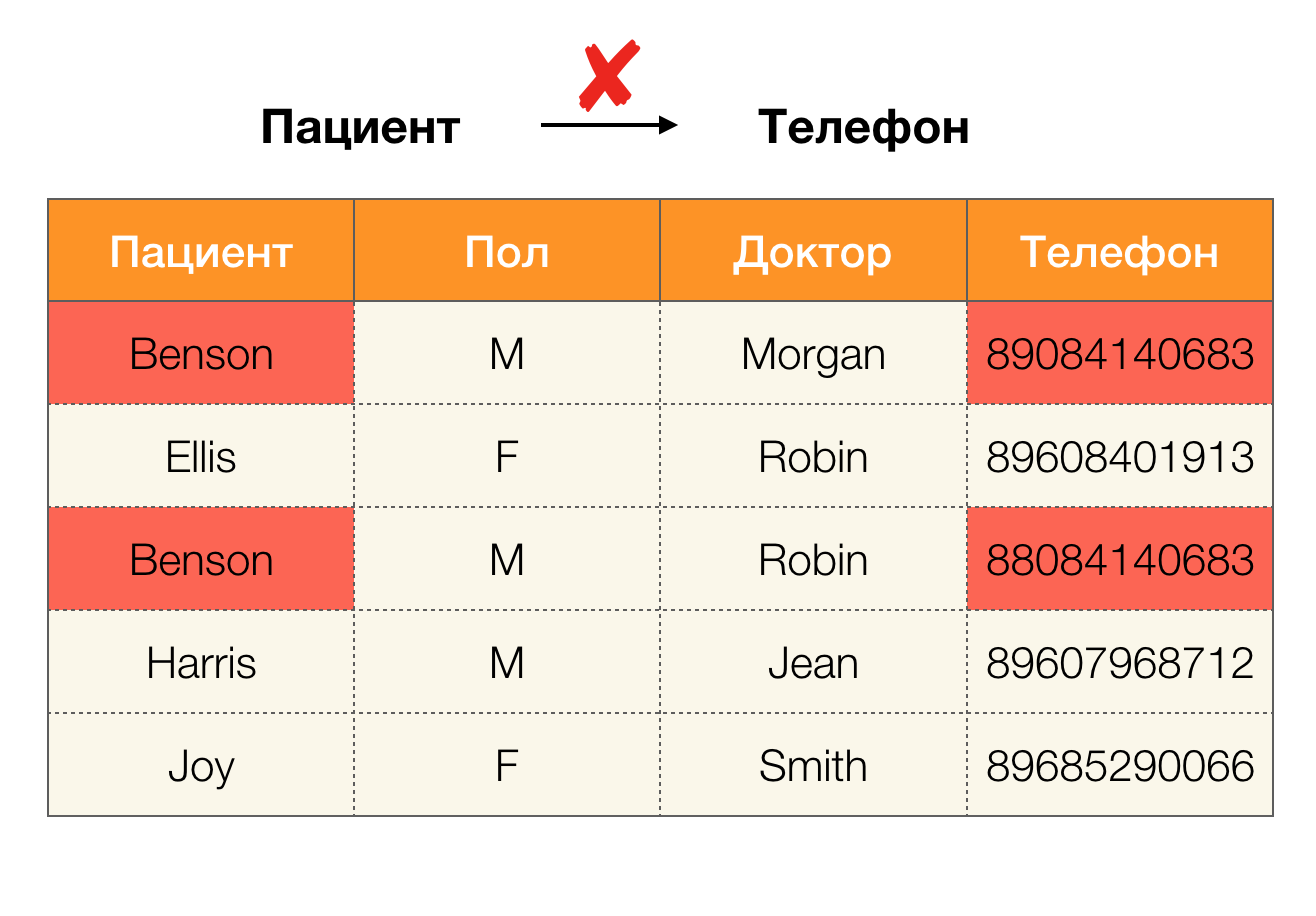
Ejemplo duplicados en datos:



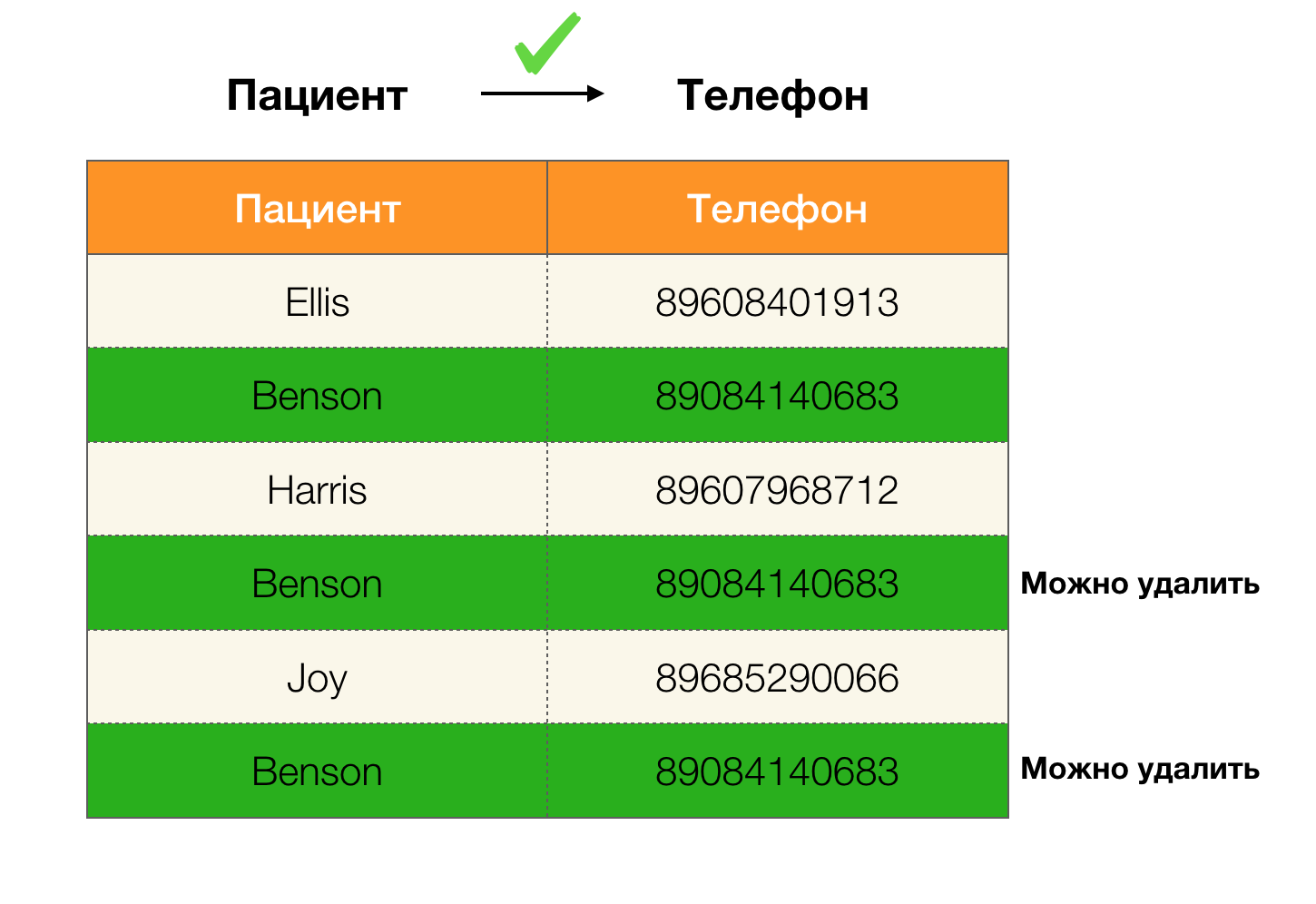
Por ejemplo, tenemos una tabla y un conjunto de leyes federales que deben ejecutarse. La limpieza de datos en este caso implica cambiar los datos para que las leyes federales sean correctas. Al mismo tiempo, el número de modificaciones debe ser mínimo (para este procedimiento, hay algoritmos en los que no nos centraremos en este artículo). El siguiente es un ejemplo de dicha conversión de datos. A la izquierda está la relación inicial, en la cual, obviamente, no se cumplen las leyes federales necesarias (un ejemplo de violación de una de las leyes federales se resalta en rojo). A la derecha hay una relación actualizada en la que las celdas verdes muestran valores cambiados. Después de tal procedimiento, las dependencias necesarias comenzaron a mantenerse.



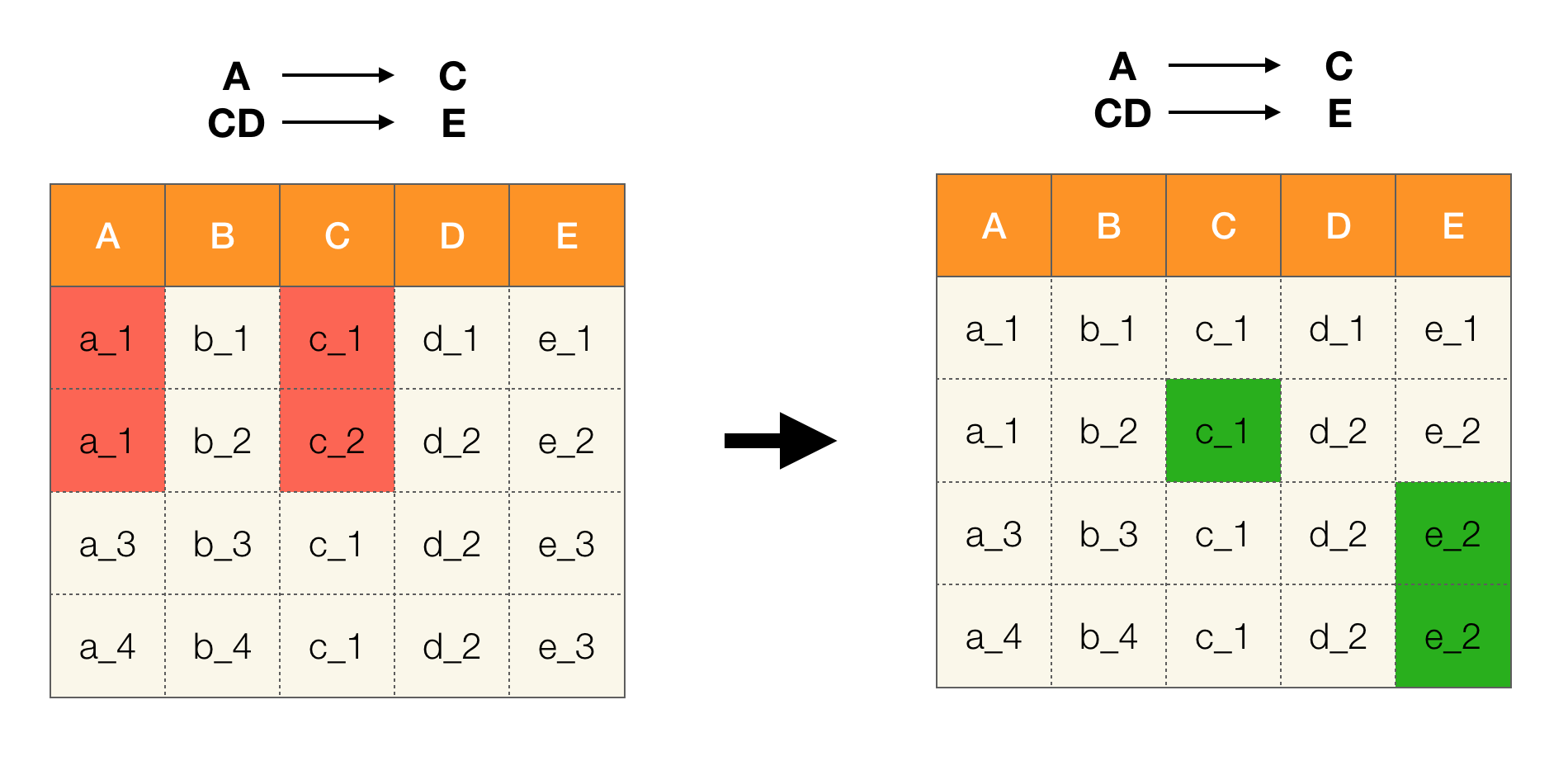
Otra aplicación popular es el diseño de bases de datos. Aquí vale la pena recordar acerca de las formas normales y la normalización. La normalización es el proceso de alinear una relación con un determinado conjunto de requisitos, cada uno de los cuales está determinado a su manera por una forma normal. No anotaremos los requisitos de varias formas normales (esto se hace en cualquier libro del curso de DB para principiantes), pero solo notamos que cada uno de ellos usa el concepto de dependencias funcionales. De hecho, las leyes federales son inherentemente restricciones de integridad que se tienen en cuenta al diseñar una base de datos (en el contexto de esta tarea, las leyes federales a veces se denominan superclaves).

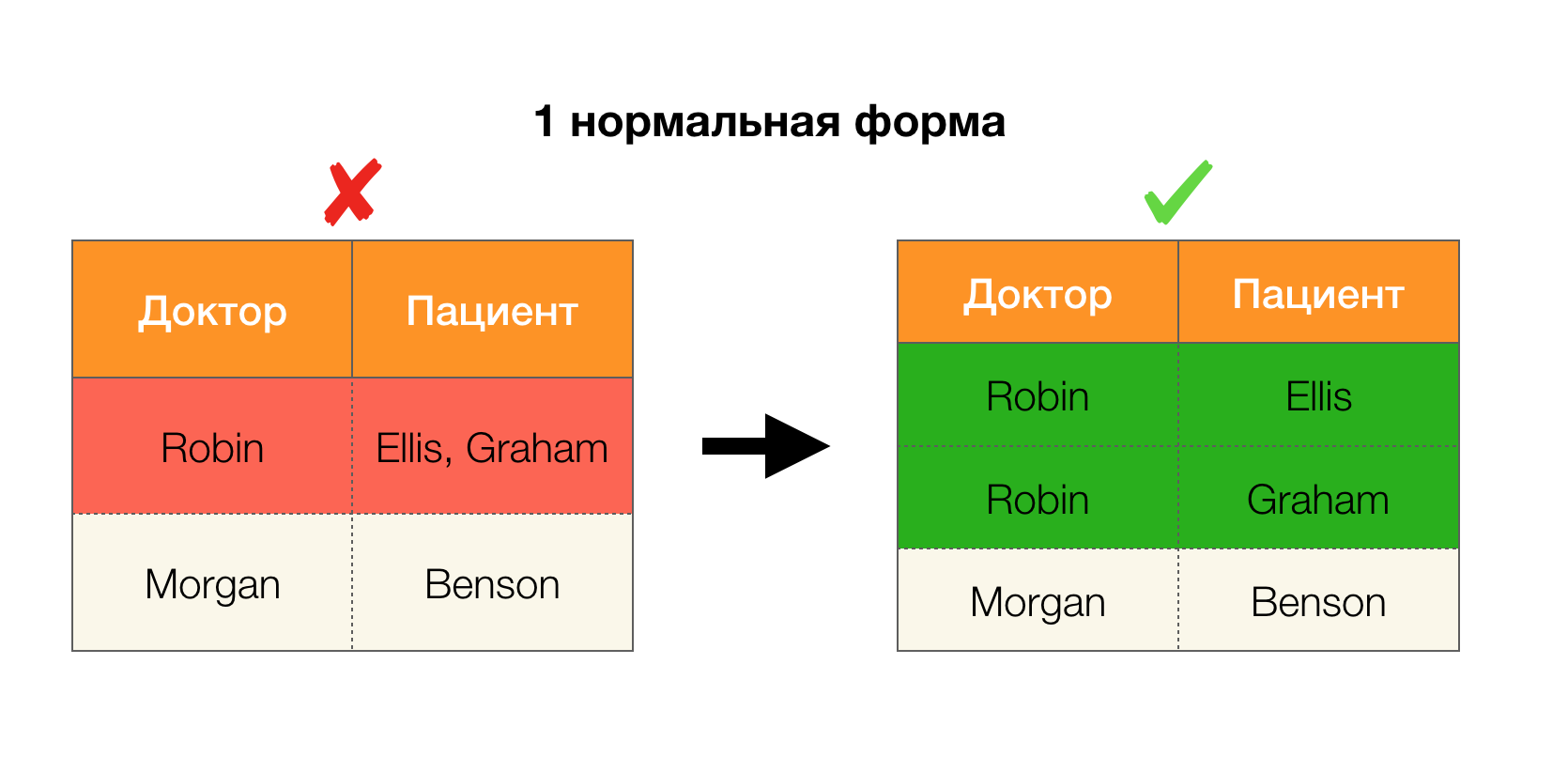
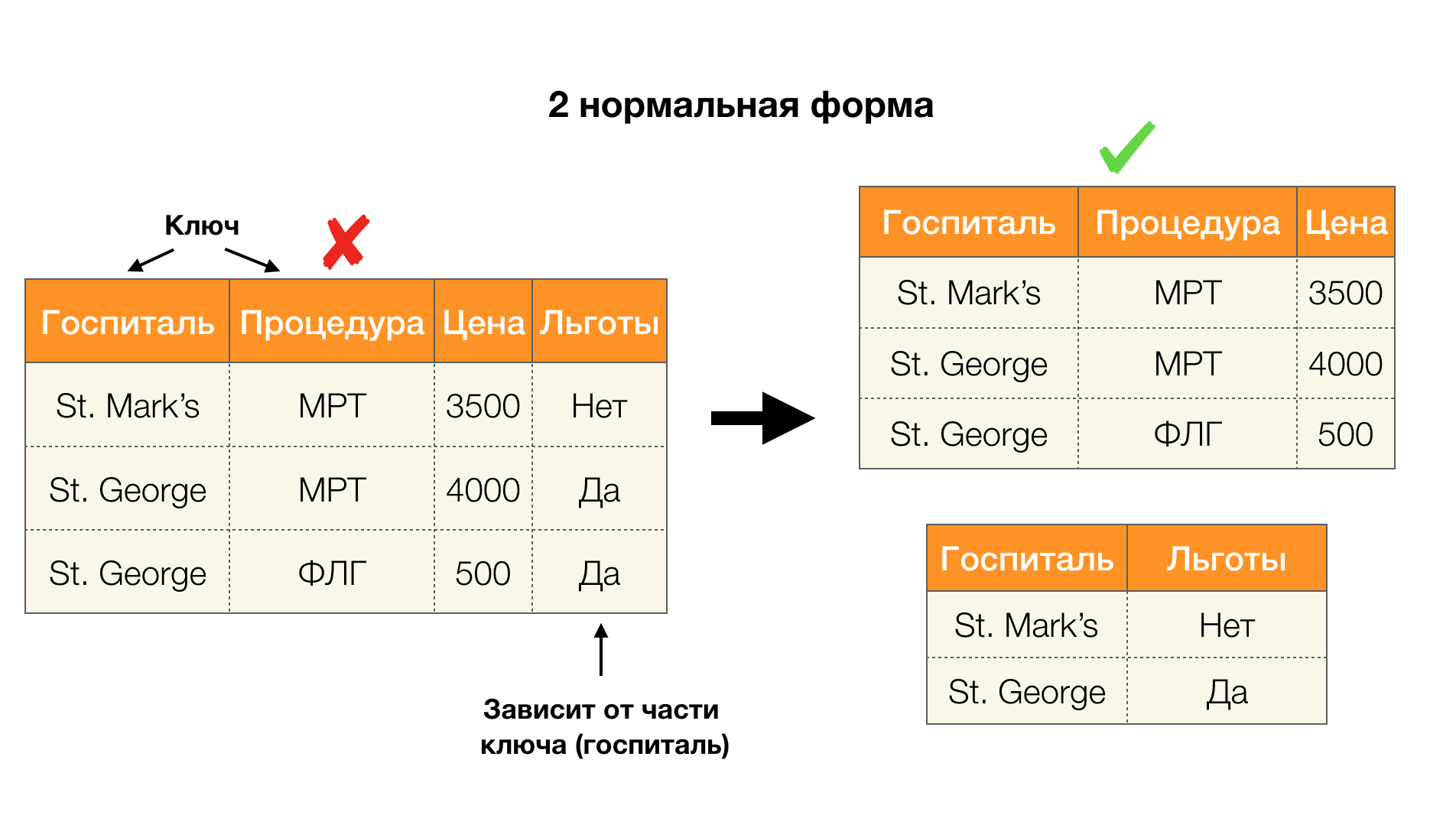
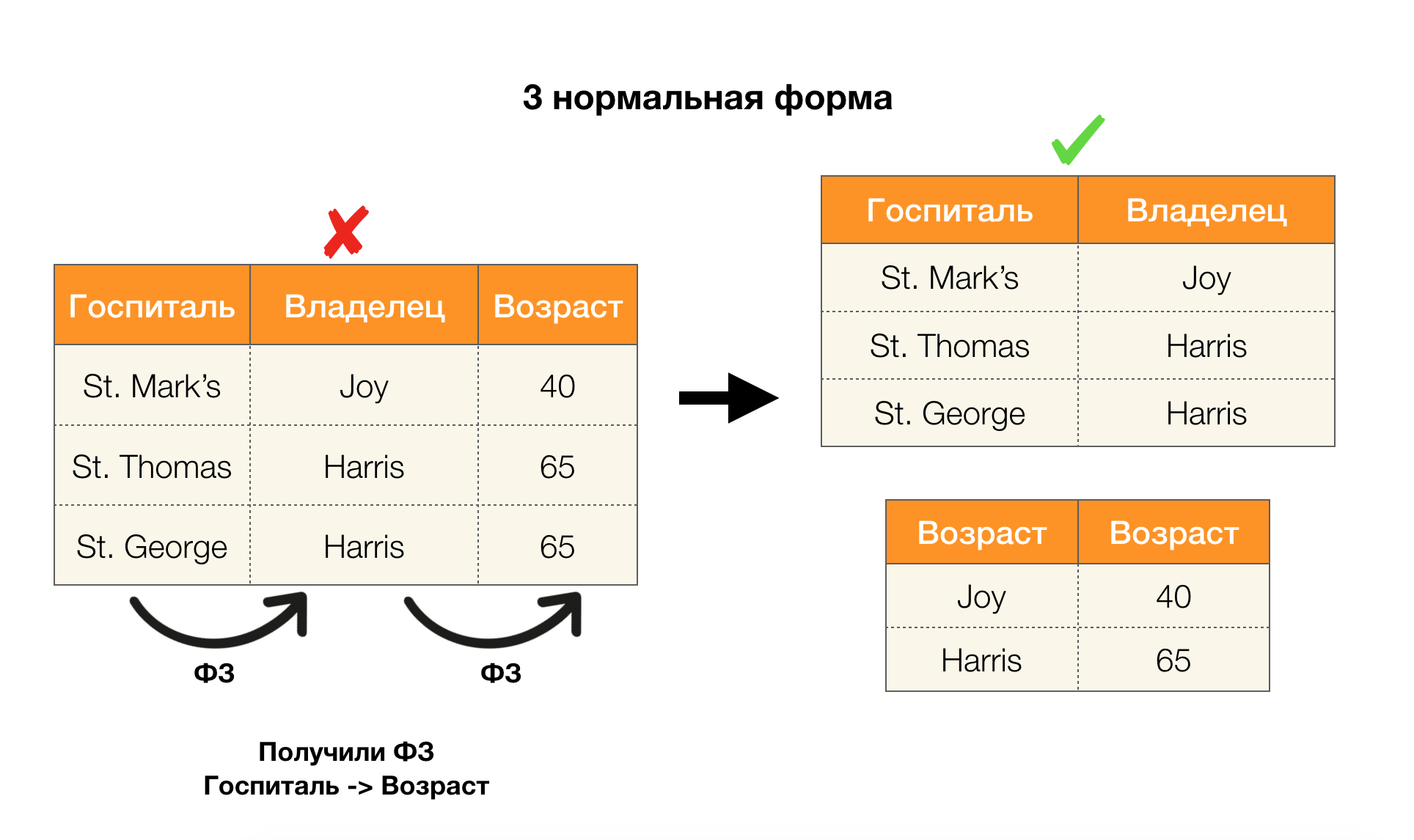
Considere su aplicación para las cuatro formas normales en la imagen a continuación. Recuerde que la forma normal de Boyce-Codd es más estricta que la tercera forma, pero menos estricta que la cuarta. Todavía no consideramos esto último, ya que su formulación requiere una comprensión de las dependencias de valores múltiples, que no nos interesan en este artículo.






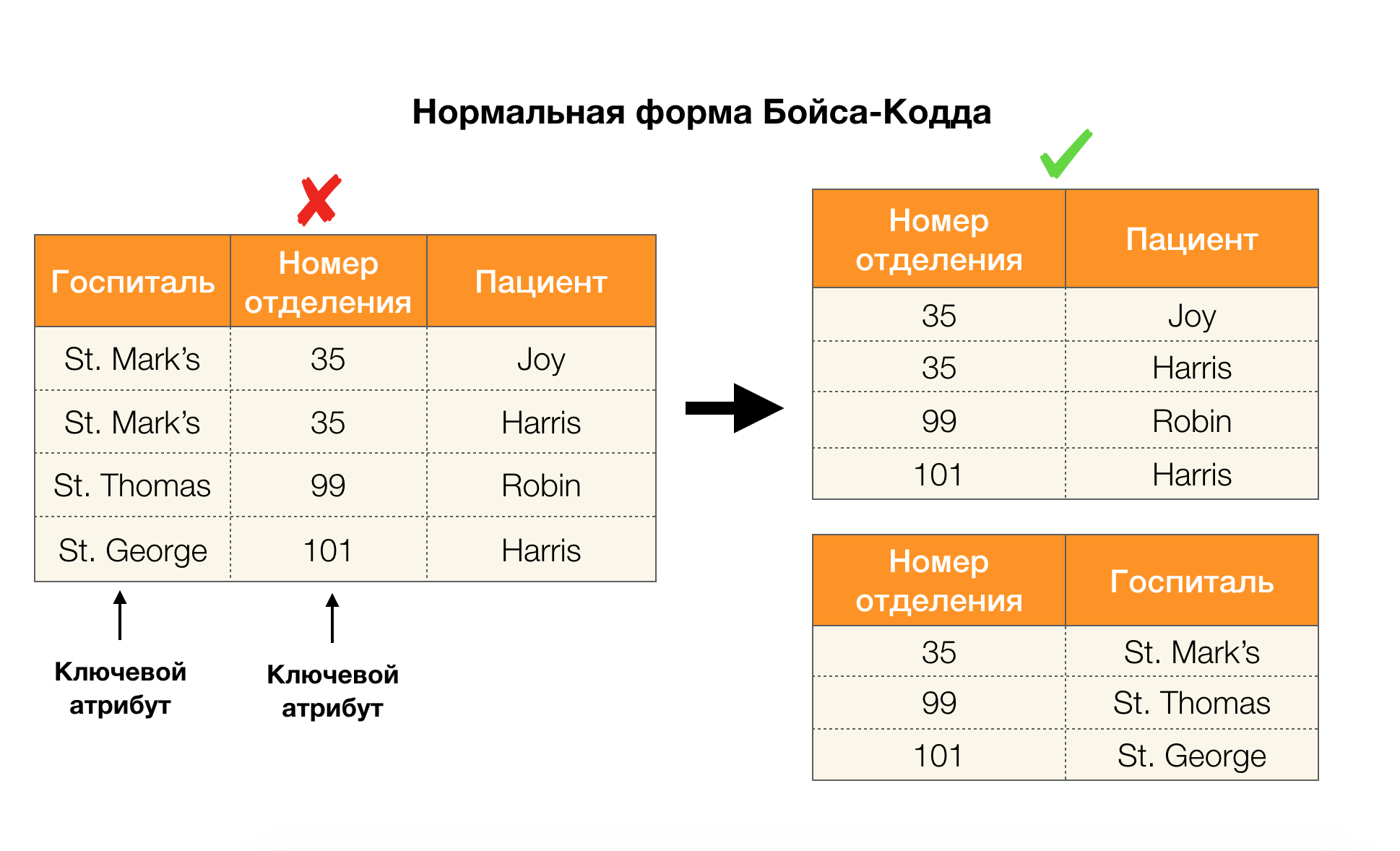
Otra área en la que las dependencias han encontrado su aplicación es la reducción de la dimensión del espacio de características en tareas tales como la construcción de un ingenuo clasificador bayesiano, la identificación de características significativas y la reparametrización del modelo de regresión. En los artículos originales, este problema se denomina definición de características redundantes (redundancia de características) y relevante (relevancia de características) [5, 6], y se resuelve con el uso activo de conceptos de bases de datos. Con el advenimiento de tales trabajos, podemos decir que hoy existe una solicitud de soluciones que permitan combinar la base de datos, el análisis y la implementación de los problemas de optimización anteriores en una sola herramienta [7, 8, 9].

Hay muchos algoritmos (tanto modernos como no muy) para buscar la Ley Federal en un conjunto de datos, que se pueden dividir en tres grupos:

• Algoritmos que utilizan el recorrido de retículas algebraicas (algoritmos transversales de celosía)
• Algoritmos basados ​​en la búsqueda de valores consistentes (algoritmos de diferencia y de acuerdo establecido)
• Algoritmos de comparación por pares (algoritmos de inducción de dependencia)
  

En la siguiente tabla se presenta una breve descripción de cada tipo de algoritmo:


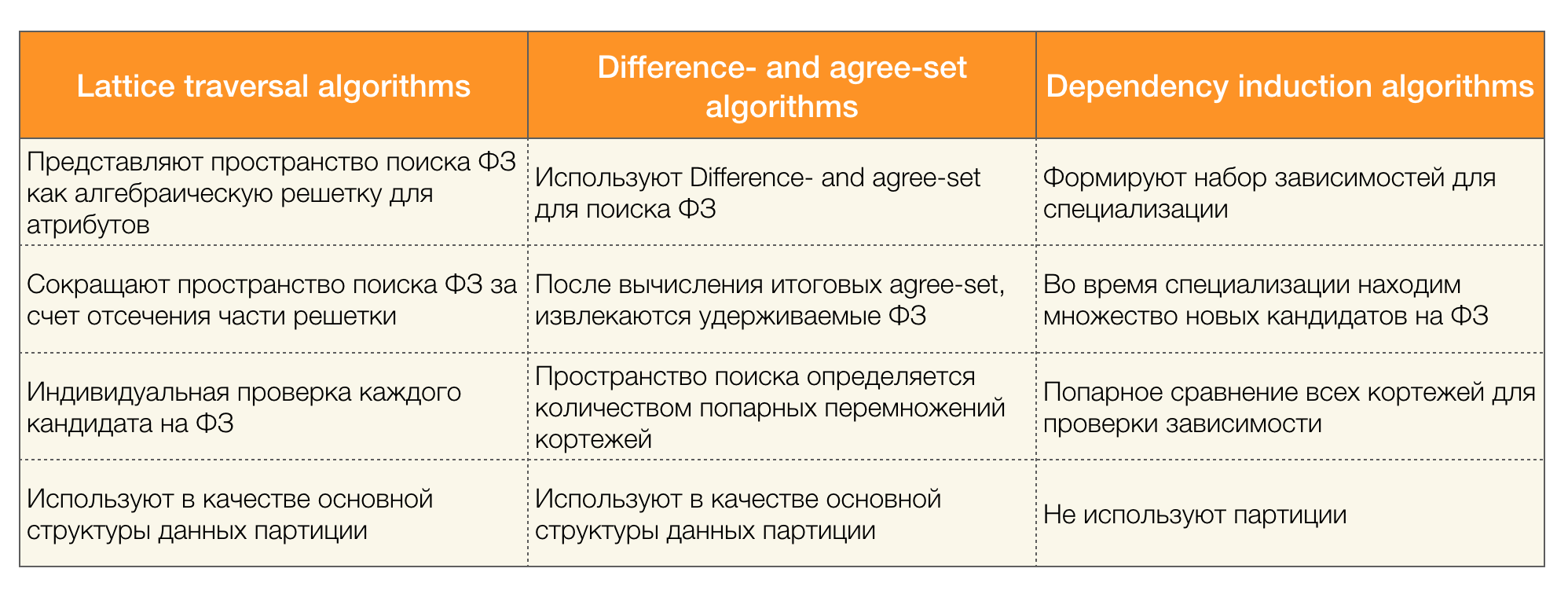
Se pueden leer más detalles sobre esta clasificación [4]. A continuación se muestran ejemplos de algoritmos para cada tipo:





Actualmente, aparecen nuevos algoritmos que combinan varios enfoques para la búsqueda de dependencias funcionales a la vez. Ejemplos de tales algoritmos son Pyro [2] y HyFD [3]. Se espera un análisis de su trabajo en los siguientes artículos de esta serie. En este artículo, solo analizaremos los conceptos básicos y el lema que son necesarios para comprender las técnicas para detectar dependencias.

Comencemos con uno simple: diferencia y conjunto de acuerdo, utilizado en el segundo tipo de algoritmos. El conjunto de diferencias es un conjunto de tuplas que no coinciden en valores, y el conjunto de acuerdo, por el contrario, son tuplas que coinciden en valor. Cabe señalar que en este caso consideramos solo el lado izquierdo de la dependencia.

También un concepto importante que se cumplió anteriormente es la red algebraica. Dado que muchos algoritmos modernos operan con este concepto, necesitamos tener una idea de lo que es.

Para introducir el concepto de una red, es necesario definir un conjunto parcialmente ordenado (o conjunto parcialmente ordenado, para abreviar).

Definición 2. Se dice que el conjunto S está parcialmente ordenado por la relación binaria ⩽ si para cualquier a, b, c ∈ S se cumplen las siguientes propiedades:

1. Reflexividad, es decir, a ⩽ a
2. Antisimetría, es decir, si a ⩽ by b ⩽ a, entonces a = b
3. La transitividad, es decir, para a ⩽ by b ⩽ c se deduce que a ⩽ c
   

Dicha relación se denomina relación de orden parcial (no estricto), y el conjunto en sí se denomina conjunto parcialmente ordenado. Notación formal: ⟨S, ⩽⟩.

Como el ejemplo más simple de un conjunto parcialmente ordenado, podemos tomar el conjunto de todos los números naturales N con la relación habitual de orden ⩽. Es fácil verificar que se cumplan todos los axiomas necesarios.

Ejemplo más significativo. Considere el conjunto de todos los subconjuntos {1, 2, 3} ordenados por la relación de inclusión ⊆. De hecho, esta relación satisface todas las condiciones de orden parcial; por lo tanto, ⟨P ({1, 2, 3}), ⊆⟩ es un conjunto parcialmente ordenado. La siguiente figura muestra la estructura de este conjunto: si desde un elemento puede caminar a lo largo de las flechas hacia otro elemento, entonces están en relación con el orden.



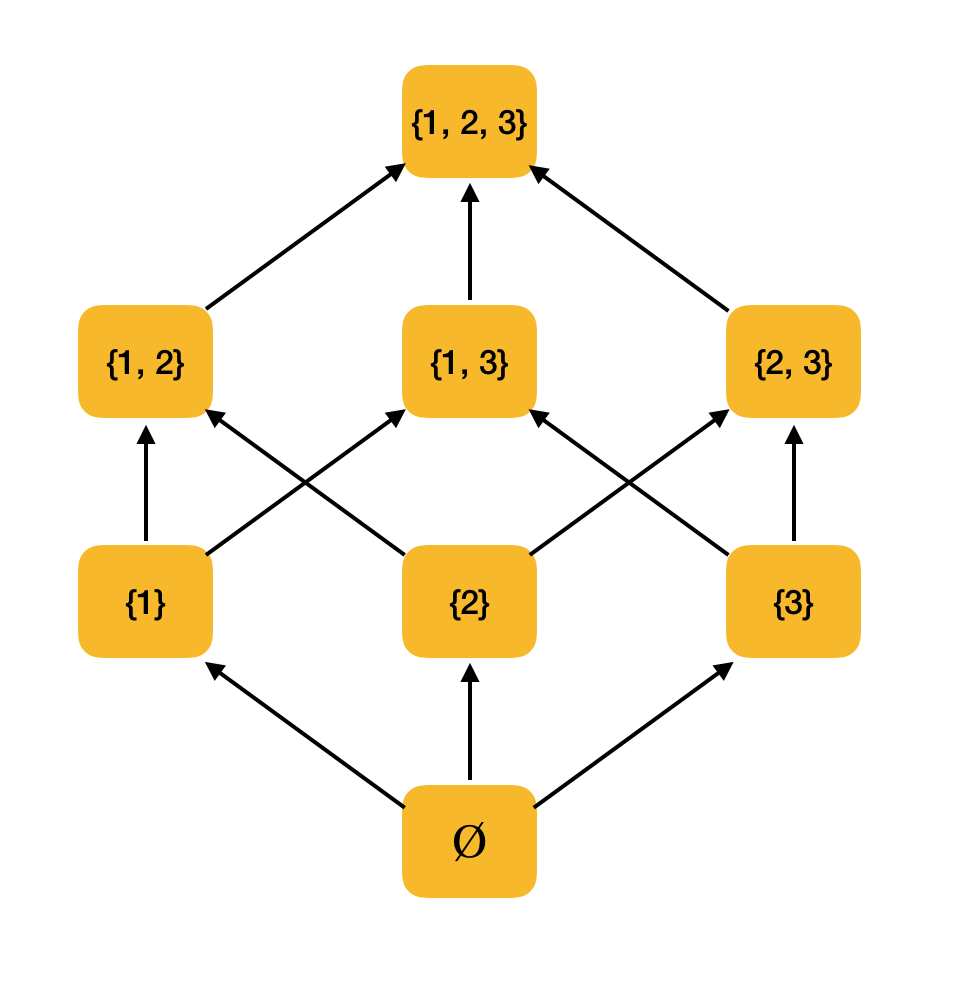
Necesitaremos dos definiciones más simples del campo de las matemáticas: supremum e infimum.

Definición 3. Sea ⟨S, ⩽⟩ un conjunto parcialmente ordenado, A ⊆ S. El límite superior de A es un elemento u ∈ S tal que ∀x ∈ A: x ⩽ u. Sea U el conjunto de todos los límites superiores de A. Si U tiene el elemento más pequeño, entonces se llama supremum y se denota por sup A.

Del mismo modo, se introduce el concepto de un límite inferior exacto.

Definición 4. Sea ⟨S, ⩽⟩ un conjunto parcialmente ordenado, A ⊆ S. El límite inferior de A es un elemento l ∈ S tal que ∀x ∈ A: l ⩽ x. Sea L el conjunto de todos los límites inferiores de A. Si L tiene el elemento más grande, entonces se llama infimum y se denota por inf A.

Considere, como ejemplo, el conjunto parcialmente ordenado anterior ⟨P ({1, 2, 3}), y encuentre el supremum y el infimum en él:



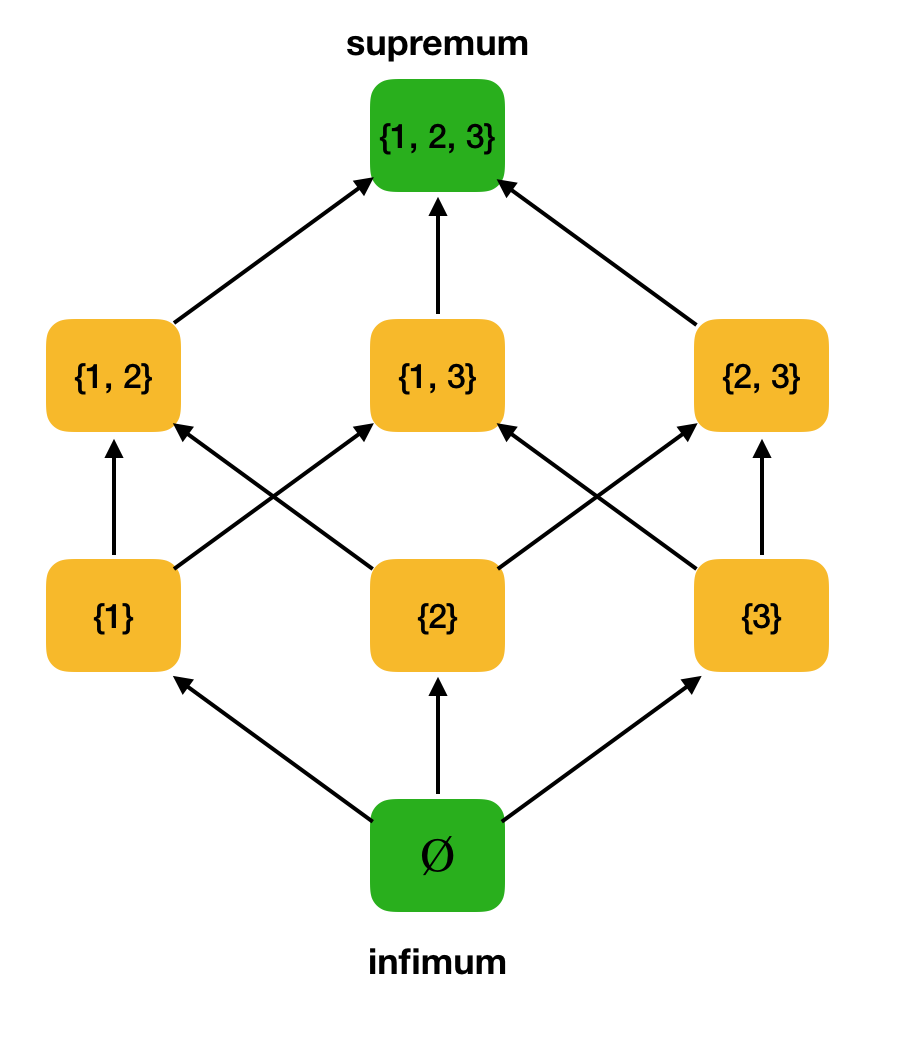
Ahora podemos formular la definición de una red algebraica.

Definición 5. Sea ⟨P, ⩽⟩ un conjunto parcialmente ordenado de manera que cada subconjunto de dos elementos tenga límites superiores e inferiores exactos. Entonces P se llama una red algebraica. Además, sup {x, y} se escribe como x ∨ y, e inf {x, y} - como x ∧ y.

Verificamos que nuestro ejemplo de trabajo ⟨P ({1, 2, 3}), ⊆⟩ es una red. De hecho, para cualquier a, b ∈ P ({1, 2, 3}), a∨b = a∪b y a∧b = a∩b. Por ejemplo, considere los conjuntos {1, 2} y {1, 3} y encuentre su infimum y supremum. Si los cruzamos, obtenemos el conjunto {1}, que será el infimum. Obtenemos el supremum por su unión - {1, 2, 3}.

En los algoritmos de detección FD, el espacio de búsqueda a menudo se representa en forma de una red, donde los conjuntos de un elemento (lea el primer nivel de la red de búsqueda, donde la parte izquierda de las dependencias consta de un atributo) son cada atributo de la relación original.
Al principio, se consideran las dependencias de la forma ∅ → atributo único. Este paso le permite determinar qué atributos son claves primarias (no hay determinantes para tales atributos y, por lo tanto, el lado izquierdo está vacío). Además, tales algoritmos se mueven hacia arriba en la red. Vale la pena señalar que la red no se puede omitir todo, es decir, si el tamaño máximo deseado de la parte izquierda se transmite a la entrada, el algoritmo no irá más allá del nivel con este tamaño.

La figura a continuación muestra cómo puede usar la red algebraica en el problema de búsqueda de la Ley Federal. Aquí, cada borde ( X, XY ) representa una dependencia X → Y. Por ejemplo, pasamos por el primer nivel y sabemos que la dependencia A → B se mantiene (lo mostraremos mediante la conexión verde entre los vértices A y B ). Por lo tanto, cuando subimos el enrejado hacia arriba, no podemos verificar la dependencia A, C → B , porque ya no será mínima. Del mismo modo, no lo probaríamos si se mantuviera la dependencia C → B.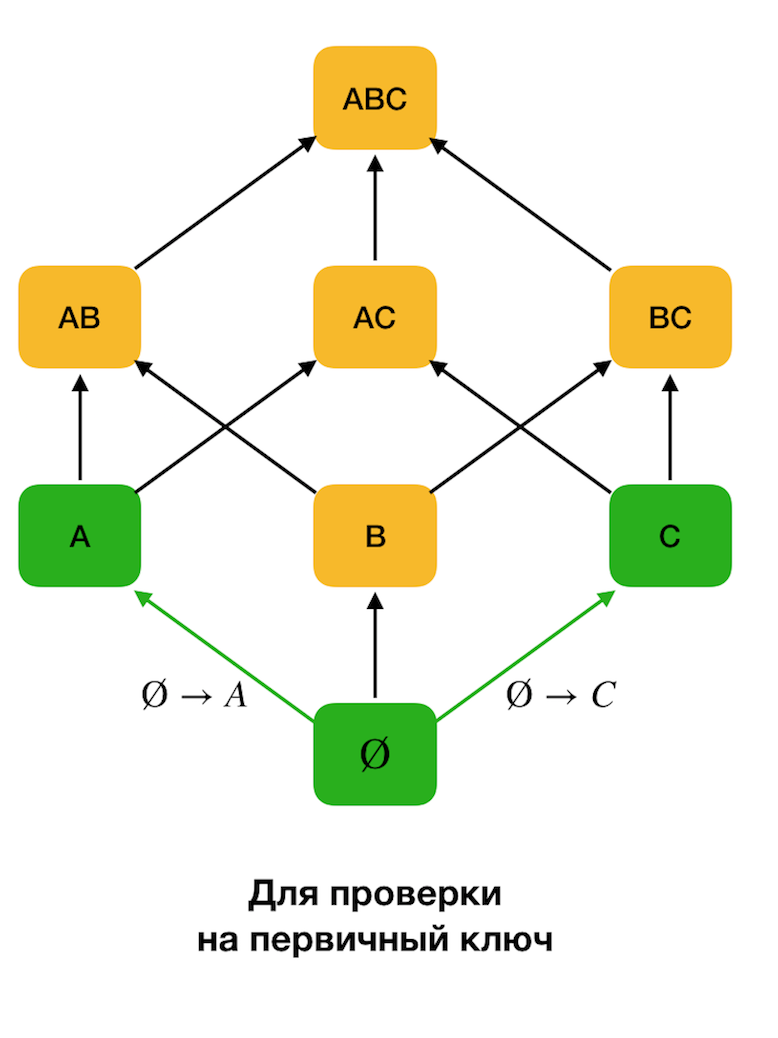




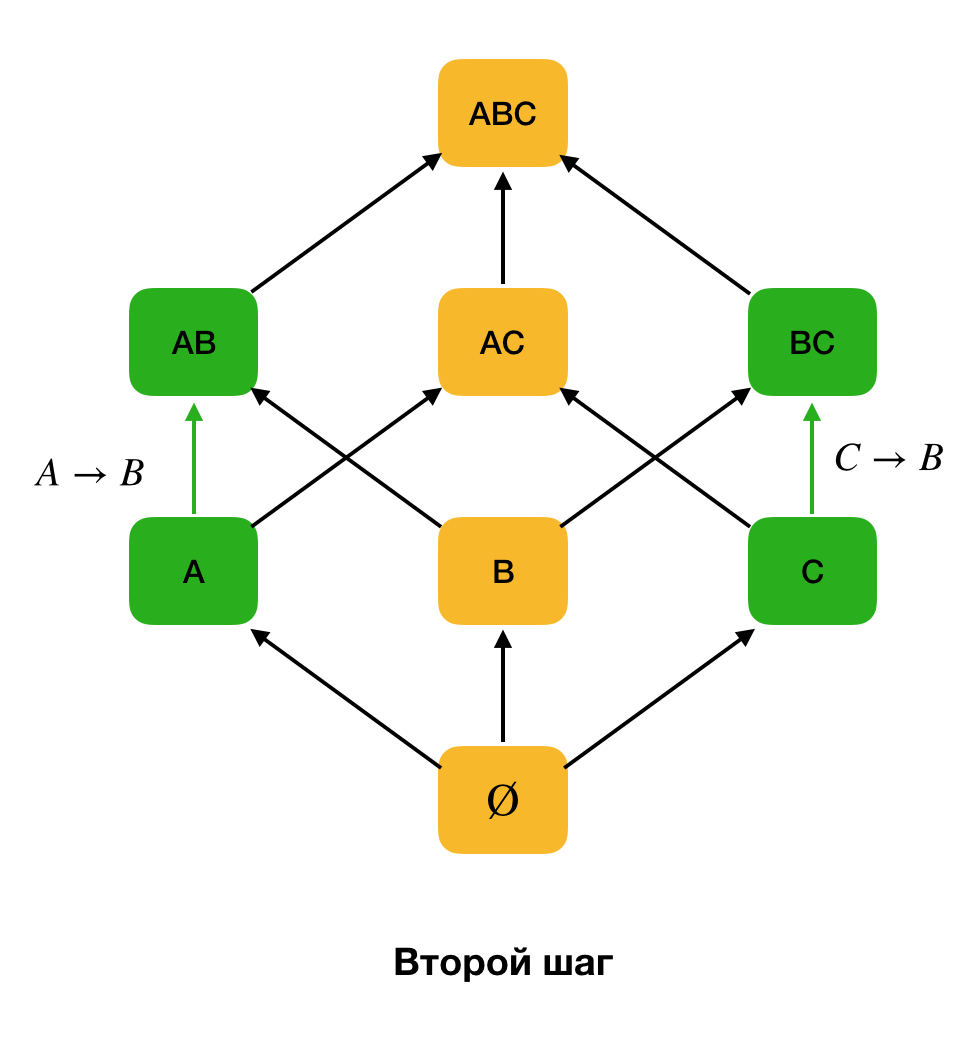
Además, como regla general, todos los algoritmos de búsqueda FZ modernos utilizan una estructura de datos como una partición (partición eliminada [1] en la fuente original). La definición formal de partición es la siguiente:

Definición 6. Sea X ⊆ R el conjunto de atributos para la relación r. Un grupo es un conjunto de índices de tuplas de r que tienen el mismo valor para X, es decir, c (t) = {i | ti [X] = t [X]}. La partición es un conjunto de grupos, excluyendo los grupos de longitud de unidad:

$$

$$\ pi (X): = \ {c (t) | t \ in r \ wedge | c (t) | > 1 \}$$

En palabras simples, la partición para el atributo X es un conjunto de listas, donde cada lista contiene números de línea con los mismos valores para X. En la literatura moderna, una estructura que representa particiones se denomina índice de lista de posición (PLI). Los grupos de longitud de unidad se excluyen para la compresión PLI porque son grupos que contienen solo un número de registro con un valor único que siempre será fácil de configurar.

Considera un ejemplo. Volvamos a la misma tabla con los pacientes y construyamos particiones para las columnas Paciente y Paul (apareció una nueva columna a la izquierda, en la que se marcan los números de fila de la tabla):





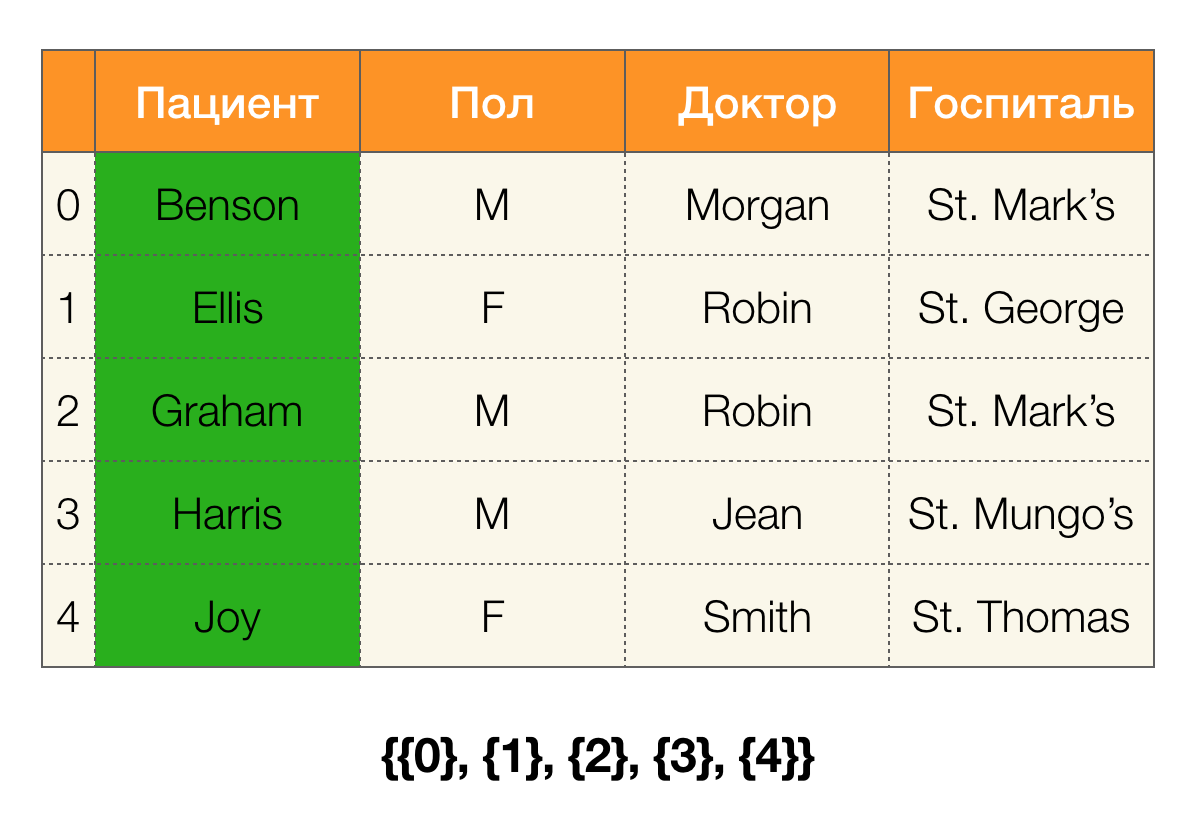
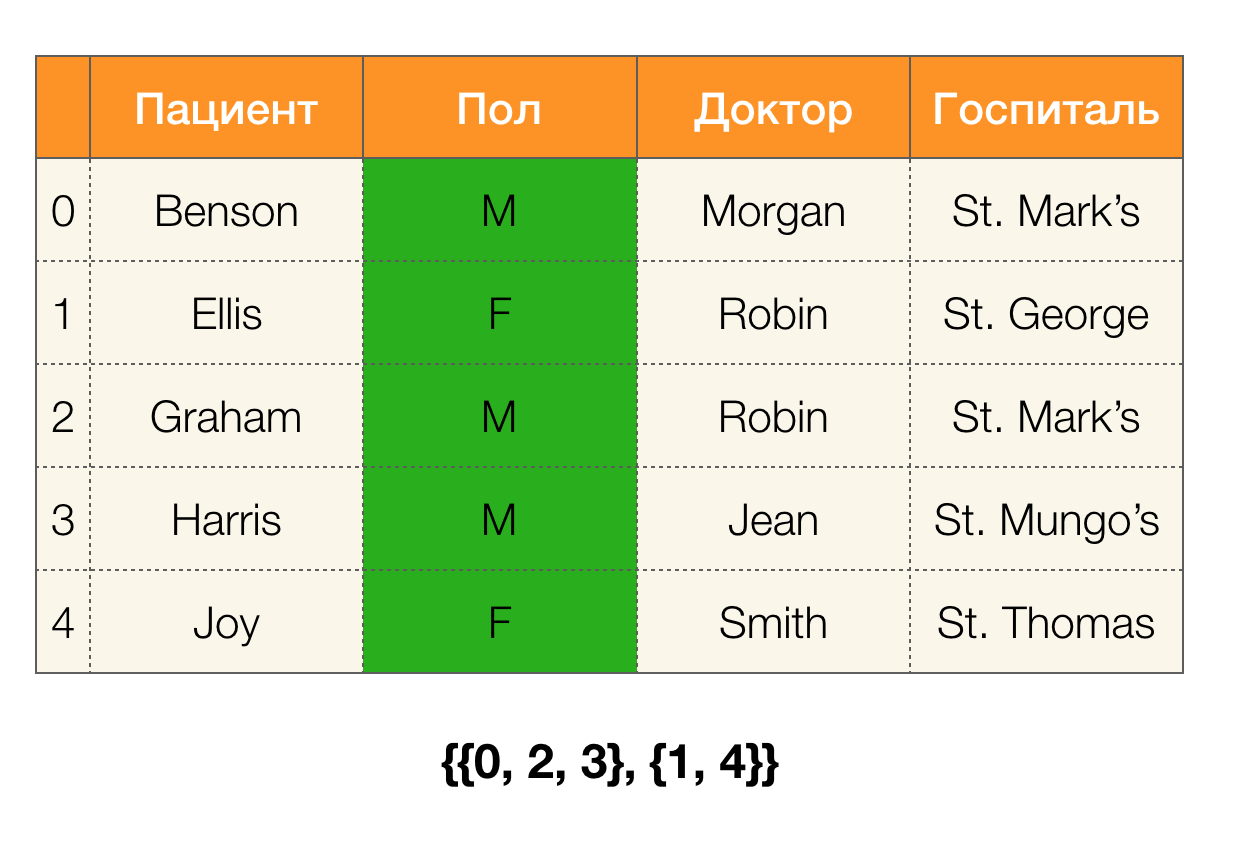
Además, según la definición, la partición para la columna Paciente estará realmente vacía, ya que los clústeres individuales están excluidos de la partición.

Las particiones se pueden obtener por varios atributos. Y para esto hay dos formas: revisar la tabla, construir una partición de una vez de acuerdo con todos los atributos necesarios, o construirla usando la operación de particiones que se cruzan por un subconjunto de atributos. Los algoritmos de búsqueda FZ usan la segunda opción.

En palabras simples, por ejemplo, para obtener una partición por columnas ABC , puede tomar particiones para AC y B (o cualquier otro conjunto de subconjuntos disjuntos) e intersecarlos entre sí. La operación de intersección de dos particiones identifica grupos de la mayor longitud común a ambas particiones.

Veamos un ejemplo:





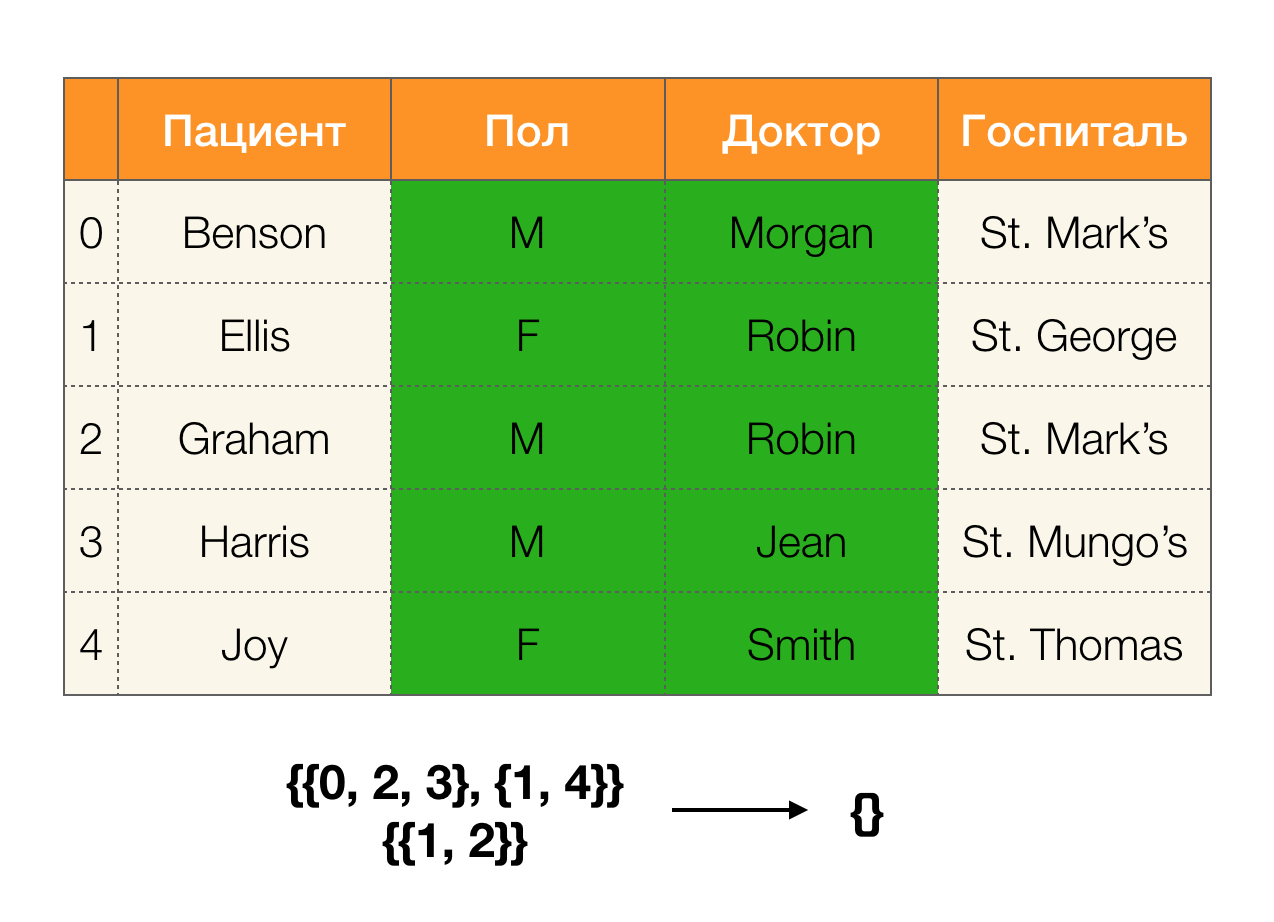
En el primer caso, recibimos una partición vacía. Si observa detenidamente la tabla, los valores idénticos para los dos atributos no están allí. Si modificamos ligeramente la tabla (el caso de la derecha), entonces ya tenemos una intersección no vacía. Al mismo tiempo, las líneas 1 y 2 realmente contienen los mismos valores para los atributos Paul y Doctor .

A continuación, necesitamos un concepto como el tamaño de la partición. Formalmente:

$$

$$| \ pi (X) | = | \ {c \ in \ pi (X): | c | > 1 \} |$$

En pocas palabras, el tamaño de la partición es el número de grupos incluidos en la partición (recuerde que los grupos individuales no están incluidos en la partición):





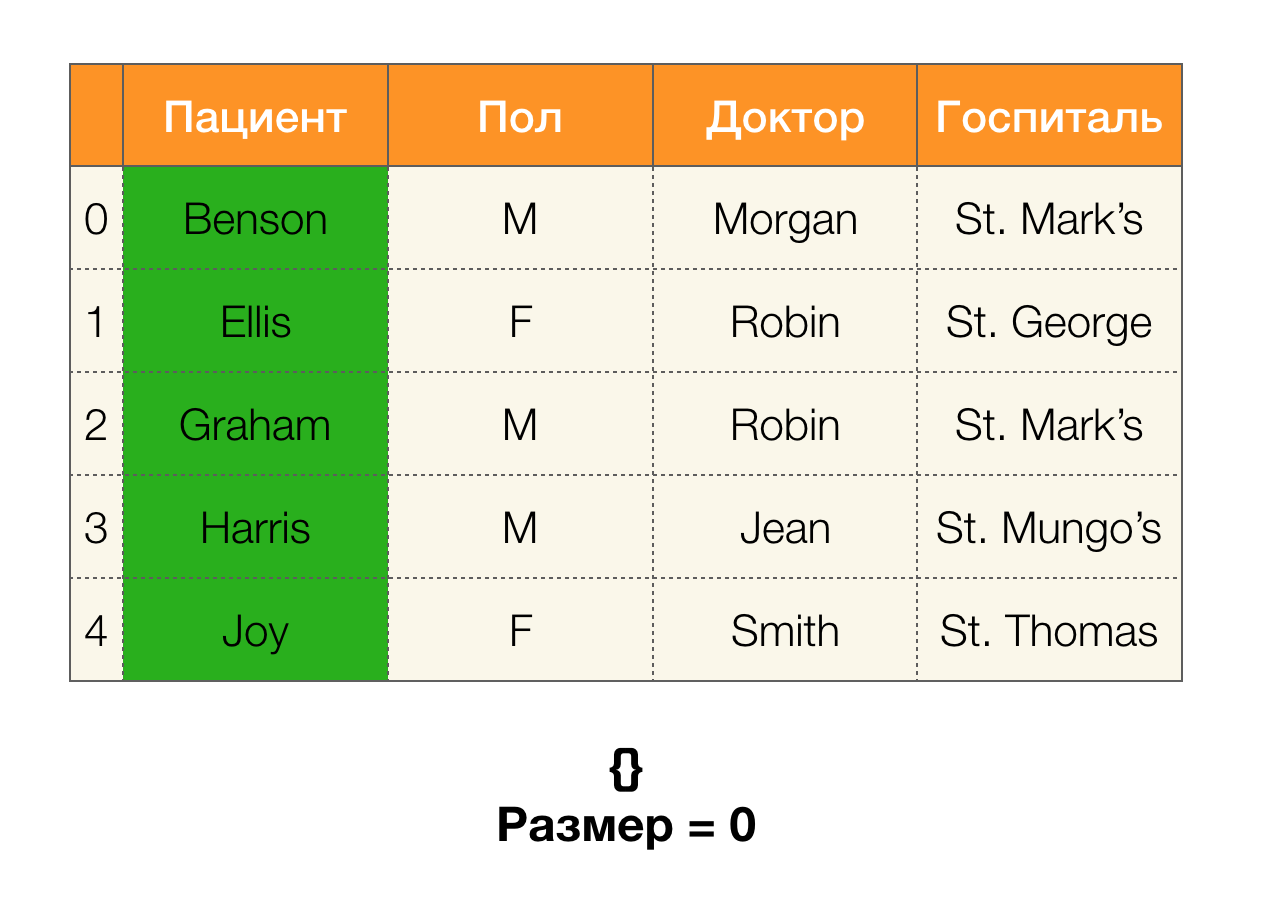
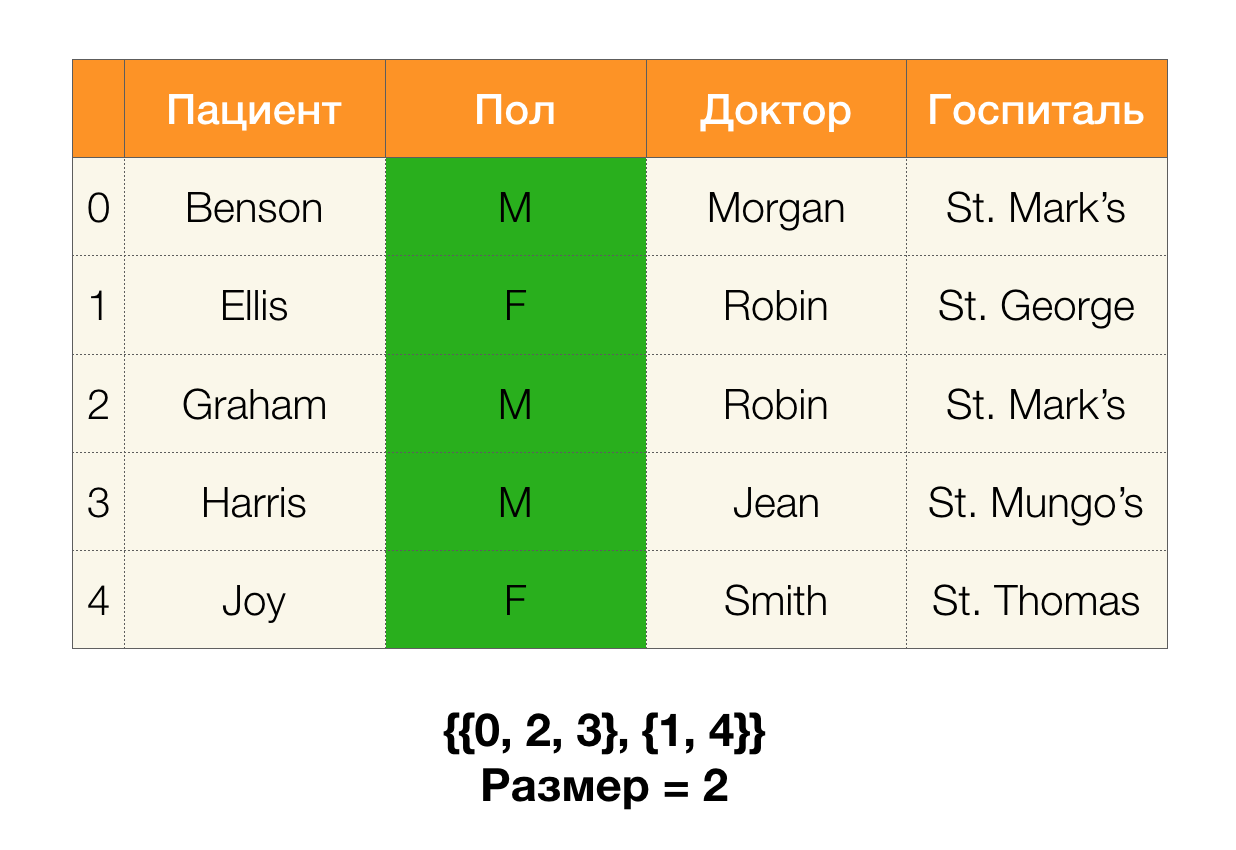
Ahora podemos definir uno de los lemas clave, que para particiones dadas nos permite establecer si la dependencia se mantiene o no:

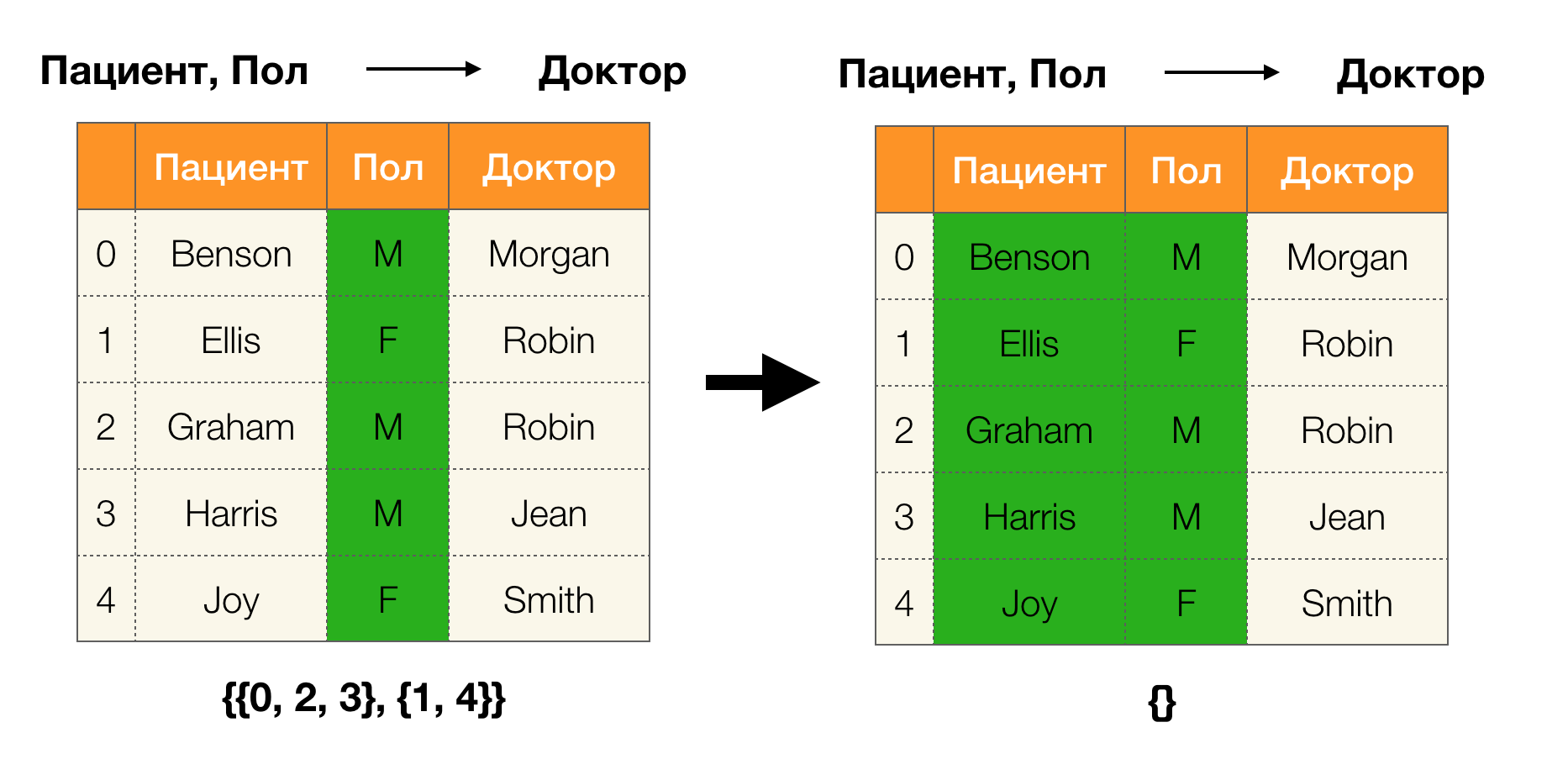
Lema 1 . La dependencia A, B → C se mantiene si y solo si

$$

$$| \ pi (AB) | = | \ pi (AB \ cup \ {C \}) |$$

Según el lema, para determinar si se mantiene una dependencia, se deben realizar cuatro pasos:

1. Calcule la partición para el lado izquierdo de la dependencia
2. Calcule la partición para el lado derecho de la dependencia
3. Calcule el producto del primer y segundo paso
   
4. Compare los tamaños de particiones obtenidas en el primer y tercer paso
   

El siguiente es un ejemplo de comprobar si este lema mantiene la dependencia:






En este artículo, examinamos conceptos como la dependencia funcional, la dependencia funcional aproximada, el lugar donde se usan y los algoritmos de búsqueda de la Ley Federal. También examinamos en detalle los conceptos básicos, pero importantes, que se utilizan activamente en algoritmos modernos para buscar leyes federales.

Referencias a la literatura:

1. Huhtala Y. y col. TANE: Un algoritmo eficiente para descubrir dependencias funcionales y aproximadas // The computer journal. - 1999. - T. 42. - No. 2. - S. 100-111.
2. Kruse S., Naumann F. Descubrimiento eficiente de dependencias aproximadas // Procedimientos de la Dotación VLDB. - 2018. - T. 11. - No. 7. - S. 759-772.
3. Papenbrock T., Naumann F. Un enfoque híbrido para el descubrimiento de dependencia funcional // Actas de la Conferencia Internacional sobre Gestión de Datos de 2016. - ACM, 2016 .-- S. 821-833.
4. Papenbrock T. et al. Functional dependency discovery: An experimental evaluation of seven algorithms //Proceedings of the VLDB Endowment. – 2015. – . 8. – №. 10. – . 1082-1093.
5. Kumar A. et al. To join or not to join?: Thinking twice about joins before feature selection //Proceedings of the 2016 International Conference on Management of Data. – ACM, 2016. – . 19-34.
6. Abo Khamis M. et al. In-database learning with sparse tensors //Proceedings of the 37th ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems. – ACM, 2018. – . 325-340.
7. Hellerstein JM et al. The MADlib analytics library: or MAD skills, the SQL //Proceedings of the VLDB Endowment. – 2012. – . 5. – №. 12. – . 1700-1711.
8. Qin C., Rusu F. Aproximaciones especulativas para la optimización de descenso de gradiente distribuido en terascala // Actas del Cuarto Taller sobre análisis de datos en la nube. - ACM, 2015 .-- S. 1.
9. Meng X. y col. Mllib: Aprendizaje automático en apache spark // The Journal of Machine Learning Research. - 2016. - T. 17. - No. 1 .-- S. 1235-1241.

Autores del artículo: Anastasia Birillo , investigadora de JetBrains Research , estudiante del centro CS y Nikita Bobrov , investigadora de JetBrains Research.