👨‍💼 🍩 👗 Julia y redes neuronales: flujo 💰 💽 🈳

Ha pasado poco más de un año desde que MIT anunció el lanzamiento del lenguaje de alto rendimiento de uso general Julia . Desde entonces, el idioma ha ganado popularidad: se usa en más de 1,500 universidades (en algunas se enseña como el primer idioma de instrucción), y los campos de aplicación abarcan desde el diagnóstico médico y la planificación de misiones espaciales hasta problemas apremiantes, como la optimización del tráfico del autobús escolar .

Uno de los campos clave de actividad de muchos proyectos, no es difícil de adivinar, es el aprendizaje automático, para el cual Julia tiene muchas herramientas poderosas , y recientemente se ha publicado un proyecto bastante interesante: el Sistema de Programación de Probabilidad General "GEN" .

Hoy prestaremos atención, como su nombre lo indica, al paquete Flux , que proporciona todo el poder de las redes neuronales. ¡Intentaremos pasar de procesar e investigar conjuntos de imágenes a una red neuronal capacitada para obtener un clasificador completo!

Sitio web oficial
Fuentes en github
La documentación
Y aquí puedes jugar con modelos entrenados

Instalación

Descargue el kit de distribución del sitio oficial e instale el intérprete de Julia ( REPL ) en su computadora.

Para que el administrador de paquetes funcione correctamente, los usuarios de Windows 7 / Windows Server 2012 también deben instalar:

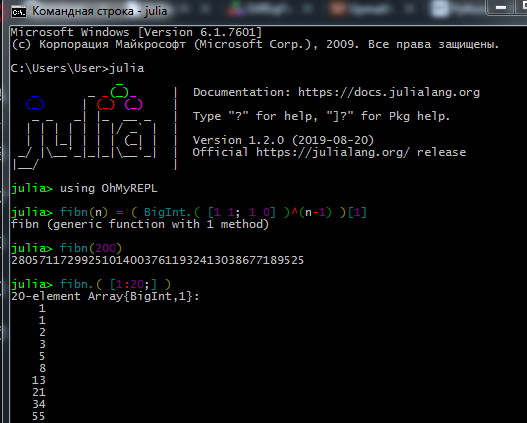
TLS easy_fix Para más detalles, vea el hilo del discurso .
Windows Management Framework 3.0 o posterior .

El proceso de trabajar en REPL se parece a esto:

Los verdaderos datasayantistas y los lingüistas de máquinas prefieren Jupyter . Aquí puede consultar la instalación, así como encontrar lecciones interactivas para el autoaprendizaje con tareas en ruso (enlaces a tutoriales originales y una guía del idioma allí).

Aquí puede ver cómo trabajar con el Jupyter Notebook.

Si hay problemas de instalación

No se puede establecer la conexión: verifique sus derechos de acceso (¿tiene restricciones para escribir en carpetas en C: \, inicie sesión como administrador o inicie Julia en modo administrador), si usa un proxy, asegúrese de que esté configurado no solo para el navegador
A algunos paquetes no les gusta el alfabeto cirílico en la ruta del archivo, por lo que debido al nombre de usuario en ruso tuve muchos problemas
Si el paquete de Interact no muestra resultados, es posible que haya instalado WebIO incorrectamente, lo que puede solucionarse
```
#]add WebIO using WebIO jup = WebIO.find_jupyter_cmd() WebIO.install_jupyter_nbextension( jup ) 
```
Para que algunos paquetes funcionen correctamente en Windows, las rutas a Julia y Jupyter deben ingresarse en variables de entorno.

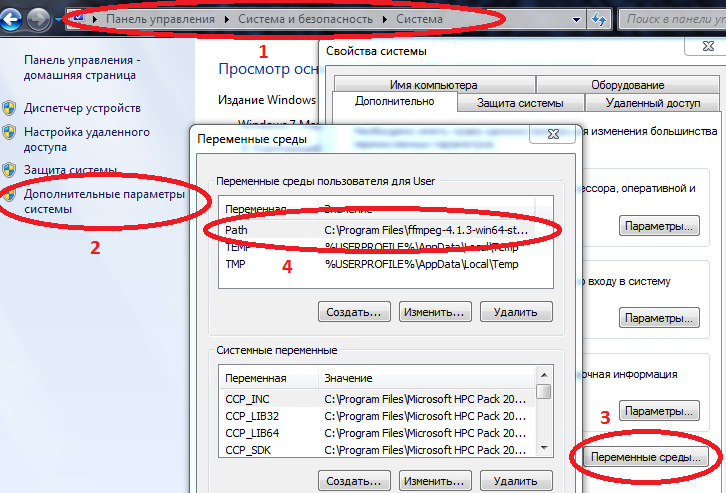
Computadora / Propiedades del sistema / Parámetros avanzados del sistema / Variables de entorno / Ruta (Crear si no) y agregue la ruta a julia.exe allí
Ejemplo C: \ Users \ User \ AppData \ Local \ Julia-1.2.0 \ bin
si Path ya tiene valores, sepárelos con un punto y coma.
Ahora, si conduce a julia a la consola de comandos ( cmd ), se iniciará el intérprete.

Una vez instalado todo lo que necesita, puede proceder a descargar los paquetes que necesita hoy. Ingrese comandos en REPL o Jupyter

Código

 using Pkg pkgs = ["Plots", "TextParse", "CSV", "DataFrames", "ImageMagick", "Images", "Interact", "Flux"] for p in pkgs Pkg.add(p) end for p in pkgs Pkg.build(p) end

Después de aprender los conceptos básicos del lenguaje (trabajar con matrices, crear funciones, descargar paquetes, trazar gráficos), puede continuar con el material posterior.

Carga y procesamiento de datos.

Recopilar y organizar datos es un arte separado. Con respecto a Julia, la red tiene mucho material desactualizado, pero primero puede probar el tutorial anterior y, para un estudio más exhaustivo, lea el libro Ciencia de datos con Julia (en el dominio público)

Y hoy, tal vez, trabajaremos con datos ya preparados: un conjunto de datos de una gran cantidad de fotografías de frutas desde varios ángulos, ¿quién quería una fruta fresca?

En realidad, esta es la tarea: ¡enseñaremos a la red neuronal a distinguir las manzanas de las bananas!

Primero lo primero, suba algunas imágenes de prueba:

 using Images fnames = [ "data/10_100.jpg", "data/107_100.jpg", "data/yellow_apple_2.jpg", "data/8_100.jpg", "data/104_100.jpg", "data/3_100.jpg" ] #   fruits = [load(fname) for fname in fnames] hcat(fruits...) #

¿Cómo difieren los objetos en las imágenes entre sí? Primero, por forma, segundo por color, y luego por texturas y otros atributos. El análisis de imágenes es un tema interesante en sí mismo, y la clasificación puede hacerse no solo por las neuronas, sino también, por ejemplo, por las wavelets . Comenzaremos con el signo más simple: el color.

Como sabe, las imágenes se almacenan en la memoria de la computadora en forma de matrices, en nuestro caso se trata de matrices, cada celda contiene tres números, que indican las cantidades de colores rojo, verde y azul en cada píxel de la imagen. Veamos la cantidad promedio de cada color en estas imágenes:

 using Statistics: mean M1 = [ mean(float.(c.(img))) for c = [red,green,blue], img = fruits ] 3×6 Array{Float32,2}: 0.570278 0.652852 0.977111 0.835252 0.903998 0.842564 0.338118 0.468729 0.950773 0.806882 0.880692 0.755442 0.322406 0.379424 0.835212 0.707626 0.799643 0.761916

Observamos cuidadosamente la primera línea, ¿no te molesta? ¡Una manzana amarilla y plátanos son más rojos que las manzanas de la variedad Breburn! ¿Cómo es eso? Vamos, invente minas agrias, tal vez los escolares estén leyendo este tutorial, o los alumnos más jóvenes del Ballet and Tractor Institute. Por lo tanto, trataremos de evitar omisiones. El hecho es que el fondo de cada imagen es blanco, y en notación RGB está representado por los valores (1,1,1). Y dado que hay 6 fondos más en las imágenes de 3 guiones, además del color de los plátanos y la manzana amarilla también contiene color rojo, resulta que las dos primeras imágenes pierden en rojo. Para mayor claridad, dividimos las imágenes en colores básicos:

 function tweaking(img) R = colorview( RGB, red.(img),zeroarray,zeroarray ) G = colorview( RGB, zeroarray,green.(img),zeroarray ) B = colorview( RGB, zeroarray,zeroarray, blue.(img) ) [R; G; B] end tweaking( hcat(fruits...) )

¿Alguna vez has escuchado la palabra críptica "base"? Entonces, podemos decir que estas imágenes se presentan en una base RGB . Cuanto más negro, menos cierto color, y como esperábamos, el fondo con su riqueza hace que el cálculo de promedios sea ruidoso. Eliminarlo

 function remove_background(img) mtrx = copy( channelview(img) ) for i = 1:size(mtrx, 2), j = 1:size(mtrx, 3) if reduce(&, mtrx[:,i,j] .> [0.8, 0.8, 0.8]) #   -  mtrx[:,i,j] .= [0.5, 0.5, 0.5] end end colorview(RGB, mtrx) end greyfruits = remove_background.(fruits)

 M3 = [ mean(float.(c.(img))) for c = [red,green,blue], img = greyfruits ] 3×6 Array{Float32,2}: 0.451008 0.532696 0.578967 0.527727 0.52849 0.500276 0.218805 0.348609 0.552679 0.499192 0.505136 0.412946 0.203528 0.260142 0.439354 0.400631 0.424784 0.419291

La diferencia en el área ocupada por cada objeto todavía está afectando, pero en general, se puede concluir que los plátanos son manzanas más verdes ( y azules ). Este será el criterio de evaluación, es decir, un signo. Ahora echemos un vistazo al resto de las imágenes:

 pth = "C:\\Users\\User\\Desktop\\Banana" # Apple Braeburn fnames = readdir(pth)[1:300] 300-element Array{String,1}: "0_100.jpg" "104_100.jpg" "107_100.jpg" "10_100.jpg" "112_100.jpg" "117_100.jpg" "118_100.jpg" "119_100.jpg" ...

Para cada imagen, neutralizamos la contribución del fondo, encontramos la cantidad promedio de cada color, recordando simultáneamente los tamaños de imagen ...

 dataz = [] for fname in fnames img_i = load("$pth\\$fname") gbimg = remove_background(img_i) colorz = [ mean(c.(gbimg)) for c = [red,green,blue] ] inform = [size(gbimg, 1) size(gbimg, 2) colorz' ] push!(dataz, inform) end dataz

... y luego puede organizar nuestros datos en estructuras convenientes para el trabajo - marcos de datos:

 using DataFrames, CSV banans = DataFrame( vcat(dataz...), [:height, :width, :red, :green, :blue] ) CSV.write("data/bananas.csv", banans) #

 apples = CSV.read("data/Apple_Braeburn.csv") #    banans = CSV.read("data/bananas.csv")

 Desc = describe(apples, :all) #

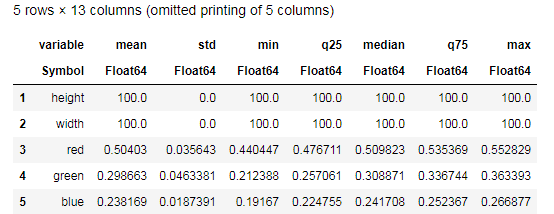
Intente comprender los datos proporcionados por la función describe() y compárelos con una tabla similar para las bananas. Bueno, ¿qué tipo de análisis de datos puede ser sin gráficos?

 function plot2features(clr) x_apples = apples[:, :green] x_banans = banans[:, :green] y_apples = apples[:, clr] y_banans = banans[:, clr] scatter(x_apples, y_apples, lab = "apples", colour = :red) scatter!(x_banans, y_banans, lab = "bananas", legend = :topleft, colour = :yellow) hline!([mean(y_apples), mean(y_banans) ], lab = "" ) vline!([mean(x_apples), mean(x_banans) ], lab = "" ) xaxis!("green") yaxis!("$clr") end plot2features(:red)

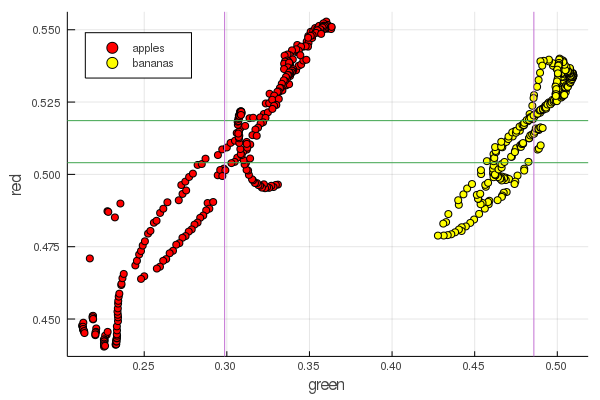
 plot2features(:blue)

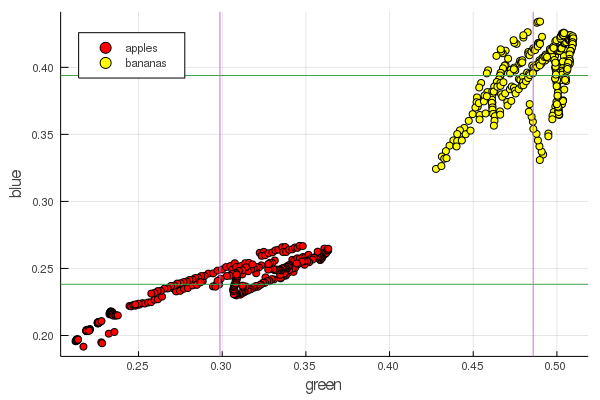
El rojo medio del plátano tiene un valor muy cercano al de la media manzana. Pero en el segundo gráfico, el aislamiento de las frutas está inmediatamente más claramente trazado por dos características de color a la vez. Las separaciones se pueden mejorar mediante la renormalización correcta, por ejemplo, nuestros valores verdes cambian de 0.2 a 0.55, y si realiza la conversión

x_{i}^{'} = f r a c x_{i} - m i n (x) m a x (x) - m i n (x)

$x_i '= \ frac {x_i - \ min (x)} {\ max (x) - \ min (x)}$

entonces obtenemos los datos reescalados en [0,1], lo que aumentará la brecha entre estos ~~montones~~ grupos de puntos.

Perceptrón

La tarea de clasificación consiste en definir un modelo y seleccionar parámetros para los cuales diversos datos recibirán de forma única una evaluación de su pertenencia a una clase en particular. En pocas palabras, necesitamos introducir una determinada función y establecer sus parámetros para que separe nuestras manzanas de las bananas.

El modelo más famoso y popular para estos fines es la neurona artificial McCulloch-Pitts, desarrollada a principios de la década de 1940. Posteriormente, Frank Rosenblatt propuso una red neuronal entrenada : el perceptrón. No es difícil encontrar explicaciones completas sobre las redes neuronales, incluido este recurso (por ejemplo, redes neuronales para principiantes , uso de redes neuronales en el reconocimiento de imágenes , redes neuronales, principios fundamentales de funcionamiento, variedad y topología )

Seleccionar el sigmoide como la función de activación y establecer las salidas de los objetos clasificados (frutas) de acuerdo con sus salidas

s i g m a (x; w, b) := f r a c 1 1 + e x p (- w x + b)

$\ sigma (x; w, b): = \ frac {1} {1 + \ exp (-wx + b)}$

x = m a t h r m d a t a

$x = \ mathrm {data}$

s i g m a (x; w, b) a p r o x 0 i m p l i c a m a t h r m a p p l e

$\ sigma (x; w, b) \ aprox 0 \ implica \ mathrm {apple}$

s i g m a (x; w, b) a p r o x 1 i m p l i c a m a t h r m b a n a n a

$\ sigma (x; w, b) \ aprox 1 \ implica \ mathrm {banana}$

seleccione tales parámetros $W$ y $b$ para que los valores de salida del sigmoide para los datos recibidos correspondan a la notación anterior

 using Interact sigmo(x,w,b) = 1 / (1 + exp(-w*x+b)) r_apples, g_apples, b_apples = apples[:, :red], apples[:, :green], apples[:, :blue] r_banans, g_banans, b_banans = banans[:, :red], banans[:, :green], banans[:, :blue]; @manipulate for w in 10:1:60, b in -5:1:25 plot(x->sigmo(x,w,b), 0, 1, label="Model", legend = :topleft, lw=3) scatter!(g_apples[1:5], zeros(10), label="Apple", colour = :red) scatter!(g_banans[1:5], ones(10), label="Banana", colour = :yellow) end

 foon(x) = sigmo(x,60,24) plot(foon, 0, 1, label="Model", legend = :topleft, lw=3) scatter!(foon, g_apples, label="Apple", colour = :red) scatter!(foon, g_banans, label="Banana", colour = :yellow) xaxis!("green")

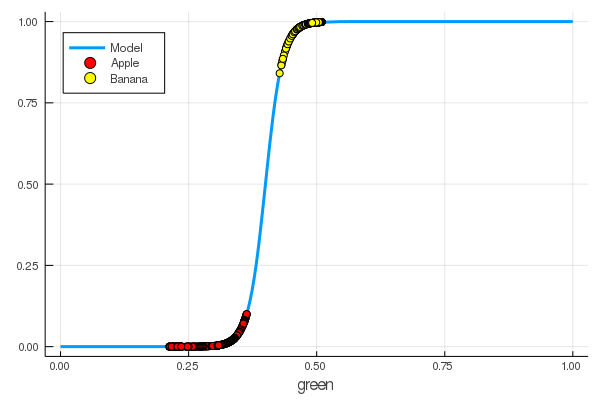
¡Enseñamos manualmente a una neurona a distinguir las manzanas de las bananas por la cantidad de verde!

Naturalmente, el deseo de automatizar este proceso. Introducimos la función de pérdida

L (w, b) = (0 - σ (x_{1}, w, b))^{2} + (1 - σ (x_{2}, w, b))^{2}

$L (w, b) = (0 - σ (x_1, w, b)) ^ 2 + (1 - σ (x_2, w, b)) ^ 2$

Ahora el proceso de aprendizaje consistirá en minimizar esta función:

Código

 apples_mean_green = mean(g_apples) banans_mean_green = mean(g_banans) L(w, b) = (0 - sigmo(apples_mean_green,w,b))^2 + (1 - sigmo(banans_mean_green,w,b))^2 w_range = 10:0.5:30 b_range = 0:0.5:20 L_values = [L(w,b) for b in b_range, w in w_range] @manipulate for w in w_range, b in b_range p1 = surface(w_range, b_range, L_values, xlabel="b", ylabel="w", cam=(80,40), cbar=false, leg=false) scatter!(p1, [w], [b], [L(w,b)+1e-2], markersize=5, color = :blue) p2 = plot(x->sigmo(x,w,b), 0, 1, label="Model", legend = :topleft, lw=3) scatter!(p2, [apples_mean_green], [0.0], label="Apple", markersize=10) scatter!(p2, [banans_mean_green], [1.0], label="Banana", markersize=10, xlim=(0,1), ylim=(0,1)) plot(p1, p2, layout=(2,1)) end

Anteriormente estudiamos paquetes para Julia que permiten resolver problemas de optimización por varios métodos. Afortunadamente, ¡lo esencial ya está en el entorno Flux!

Flujo

 using Flux

Primero, presentamos los datos para el entrenamiento en una forma digerible:

 Y = [zeros(length(g_apples)); ones(length(g_banans)) ] |> permutedims X = [g_apples; g_banans] |> permutedims; #   -   # dataz = repeated((X, Y), 20)

Siguiente en orden:

Creamos un conjunto de datos de entrenamiento combinando los datos de entrada con las respuestas correctas con respecto a la clasificación de estos datos.
Establecemos los parámetros W y b por matrices de valores aleatorios (hay un signo en la entrada y otro en la salida, por lo que las matrices tienen un tamaño de 1 x 1 )
Como modelo, establecemos una capa densa : un perceptrón con una función de activación sigmoidal.
Establecemos la función de pérdida: la suma de las diferencias al cuadrado (aún puede usar el Flux.crossentropy() más popular)
Como método de optimización, elegimos el descenso por gradiente . Toma un parámetro: la velocidad de descenso
Establecemos una función de evaluación que redondeará los valores de los resultados del modelo y los comparará con las respuestas correctas.
E imprima los parámetros de nuestro modelo no entrenado

 dataz = [(X, Y)] W = param(rand(1)) b = param(rand(1)) model = Dense(W, b, σ) loss(x, y) = mse(model(x), y) opt = Descent(0.1) accuracy(x, y) = mean( round.(model(x)) .== y ) params(model) Params([[0.3372841444115968] (tracked), [0.8430399003786011] (tracked)])

Veamos cuál es el resultado de la función de pérdida para nuestros datos.

 loss(X, Y) #  ,   0.310845210182773 (tracked)

Y verifique los resultados de la función de evaluación

 accuracy(X, Y) 0.5

El resultado es bastante natural: las salidas se distribuyen de manera bastante uniforme y la mitad de los datos se clasifican correctamente:

Código

 modeldataz(x) = x |> model |> data |> permutedims # modeldataz(x) = permutedims(data(model(x)))

 modelX = modeldataz(X) modelapples = modeldataz(g_apples') modelbanans = modeldataz(g_banans') plot(modelX, legend = false) hline!([0.5]) p1 = yaxis!((0,1)) curv = [-1:0.01:1;]' |> modeldataz plot( [-1:0.01:1;], curv, label="Model", legend = :topleft, lw=3) scatter!(g_apples, modelapples, label="Apple", colour = :red) scatter!(g_banans, modelbanans, label="Banana",colour = :yellow) hline!([0.5], lab = "", legend = :topleft) p2 = xaxis!("green") plot(p1, p2)

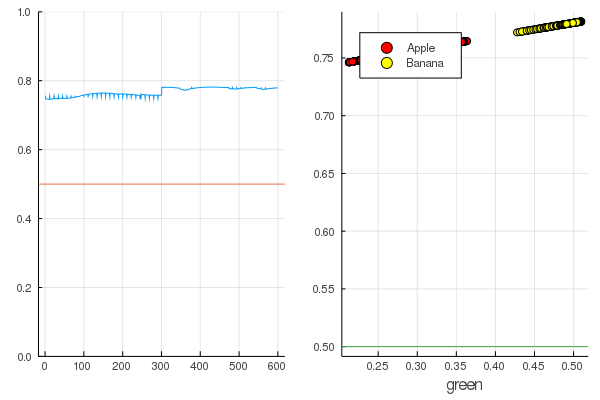
Comencemos: es bastante simple. Solo necesita gritarle a la red neuronal: "¡Entrena!", Mientras indica qué entrenar y qué minimizar, y ella completará una sesión de entrenamiento. Por lo tanto, la obligaremos a destetar todo como debería, pero solo sin fanatismo, para que no haya reciclaje.

 for i in 1:7000 train!(loss, params(model), dataz, opt) end model.W, model.b ([9.578663260720564] (tracked), [-3.7540362587506464] (tracked))

Las pérdidas se han vuelto mucho menos:

 loss(X, Y) 0.09152783090457564 (tracked)

Una calificación es mejor:

 accuracy(X, Y) 1.0

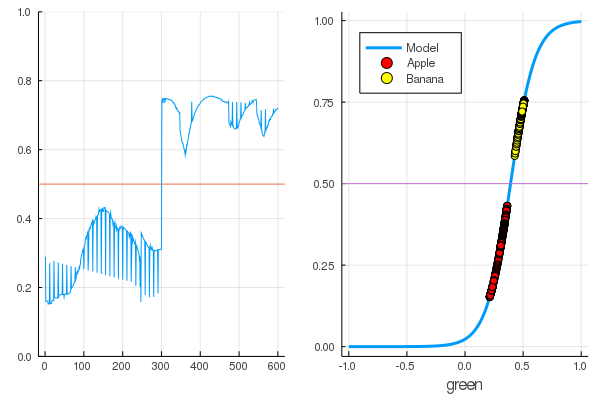
Los datos se dividen y una formación adicional hará que el modelo funcione más verticalmente. Verifique el modelo entrenado en el primer conjunto de frutas:

 function classifier(img) gbimg = remove_background(img) greenmean = mean(float.(green.(gbimg))) answ = data( model( [ greenmean ]' ) )[1] fr = answ > 0.5 ? "Banana" : "Apple" "$fr $(round(200abs(0.5-answ)))%" end hcat(fruits...)

 classifier.(fruits) 6-element Array{String,1}: "Apple 68.0%" "Apple 20.0%" "Banana 65.0%" "Banana 47.0%" "Banana 49.0%" "Banana 10.0%"

Una manzana amarilla especialmente plantada, por supuesto, no fue reconocida correctamente, y un plátano rojo apenas entró en su categoría. Pero la neurona solo obtiene un número de la imagen: la cantidad promedio de verde. Puede agregar otro signo, por ejemplo, la cantidad de azul, lo que hará que el modelo sea un poco más adaptable.

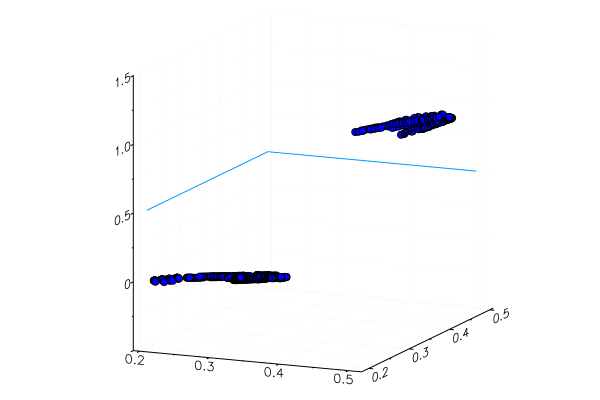
O puede usar no la representación RGB, sino HSV (tono, saturación, valor), en el que el canal de tono contendrá información sobre el color de la imagen.

Todo el placer de las redes neuronales es que ellos mismos pueden distinguir características que a veces no son muy obvias (correlación de colores, su distribución, contornos y curvas ...), y puede ayudarlos con la ayuda de técnicas y heurísticas especiales, lo que convierte el trabajo con redes neuronales en arte real

Para que el liderazgo no crezca demasiado ~~y hacer una serie de artículos demasiado flojos~~ ¡Déjenos también dar un ejemplo de la clasificación de imágenes con números escritos a mano, y el lector interesado generalizará el conocimiento adquirido en imágenes con frutas y creará su propia red neuronal, capaz de, digamos, marcar objetos en bodegones!

Mnist

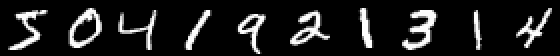
 using Images using Flux, Flux.Data.MNIST, Statistics using Flux: onehotbatch, onecold, crossentropy, throttle using Base.Iterators: repeated # using CuArrays # Classify MNIST digits with a simple multi-layer-perceptron imgs = MNIST.images() # Stack images into one large batch X = hcat(float.(reshape.(imgs, :))...); hcat(imgs[1:10]...)

Un ejemplo es interesante porque ya hay diez salidas. Los llamados vectores One-hot son útiles aquí.

 labels = MNIST.labels() # One-hot-encode the labels Y = onehotbatch(labels, 0:9)

 10×60000 Flux.OneHotMatrix{Array{Flux.OneHotVector,1}}: 0 1 0 0 0 0 0 0 0 0 0 0 0 … 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 … 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0

Definimos una cadena de neuronas como modelo, la entropía cruzada será una función de pérdida y Adam como método de optimización:

 m = Chain( Dense(28^2, 32, relu), Dense(32, 10), softmax) loss(x, y) = crossentropy(m(x), y) accuracy(x, y) = mean(onecold(m(x)) .== onecold(y)) dataset = repeated((X, Y), 20) evalcb = () -> @show(loss(X, Y)) opt = ADAM()

Entrena en modo ahorrador, pero imprime las pérdidas cada 10 segundos:

 for i = 1:10 Flux.train!(loss, params(m), dataset, opt, cb = throttle(evalcb, 10)) end #   ...

 accuracy(X, Y) 0.64545

Y verifique los datos no utilizados en el entrenamiento

 # Test set accuracy tX = hcat(float.(reshape.(MNIST.images(:test), :))...) tY = onehotbatch(MNIST.labels(:test), 0:9) accuracy(tX, tY) 0.6488

¡Las redes neuronales en Julia son simples y muy emocionantes! Incluso si no hay necesidad de buscar conexiones entre su campo de actividad y el aprendizaje automático, al menos debe sentir esta curiosidad, que se grita desde todos los ángulos, ¡y no faltarán herramientas!

¡Todo el calor moderado de la CPU!

Julia y redes neuronales: flujo

Instalación

Carga y procesamiento de datos.

Perceptrón

Flujo

Mnist

More articles: