Análisis detallado del método simplex

Prologo

Recientemente, era necesario crear un programa desde cero que implementara el algoritmo del método simplex. Pero en el curso de la solución, me encontré con un problema: no hay tantos recursos en Internet donde pueda ver un análisis teórico detallado del algoritmo (su razón de ser: por qué tomamos estos o esos pasos) y consejos prácticos de implementación, directamente, el algoritmo. Luego me hice una promesa: tan pronto como complete la tarea, escribiré mi publicación sobre este tema. En realidad, hablaremos de esto.

Observación La publicación se escribirá en un lenguaje bastante formal, pero recibirá comentarios, lo que debería aportar cierta claridad. Tal formato preservará el enfoque científico y, al mismo tiempo, puede ayudar a algunos en el estudio de este tema.

§1. Declaración del problema de programación lineal.

Definición: La programación lineal es una disciplina matemática dedicada a la teoría y los métodos para resolver problemas extremos en conjuntos de espacios n-dimensionales definidos por sistemas de ecuaciones lineales y desigualdades.

La tarea general de la programación lineal (en adelante, LP) tiene la forma:

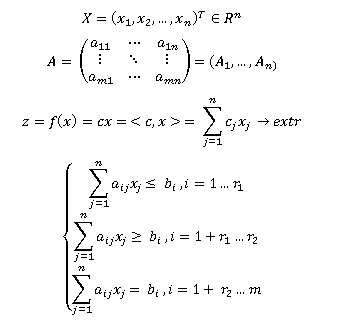
§2. La forma canónica del problema de LP

La forma canónica del problema de LP:



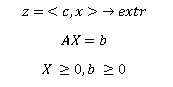Nota: Cualquier problema de LP se reduce a canónico.

El algoritmo para la transición de un problema de LP arbitrario a la forma canónica:

1. Desigualdades con negativo$$ $ en línea $ b_i $ en línea $ multiplicar por (-1).
2. Si hay una desigualdad de la forma (≤), entonces agregue al lado izquierdo$$ $ en línea $ s_i $ en línea $ Es una variable adicional, y obtenemos igualdad.
3. Si hay una desigualdad en la forma (≥), restar del lado izquierdo$$ $ en línea $ s_i $ en línea $ , y obtenemos la igualdad.
4. Hacemos el reemplazo de variables:

• Si$$ $ en línea $ x_i ≤ 0 $ en línea $ entonces$$ $ en línea $ x_i '= -x_i ≥ 0 $ en línea $
• Si$$ $ en línea $ x_i $ en línea $ - cualquiera$$ $ en línea $ x_i = x_i '- x_i' '$ en línea $ donde$$ $ en línea $ x_i ', x_i''≥ 0 $ en línea $

Nota: numeraremos$$ $ en línea $ s_i $ en línea $ por el número de desigualdad al que lo agregamos.

Nota:$$ $ en línea $ s_i $ en línea $ ≥0.

§3. Puntos de esquina. Variables básicas / libres. Soluciones basicas

Definición: Punto$$ $ en línea $ X ∈ D $ en línea $ llamado un punto de esquina si la representación$$ $ en línea $ X = αX ^ 1 + (1-α) X ^ 2, donde X ^ 1, X ^ 2 ∈ D; 0 <α <1 $ en línea $ solo posible con$$ $ en línea $ X ^ 1 = X ^ 2 $ en línea $ .

En otras palabras, es imposible encontrar dos puntos en la región, el intervalo de paso que contiene$$ $ en línea $ X $ en línea $ (es decir$$ $ en línea $ X $ en línea $ No es un punto interno).

El método gráfico para resolver el problema de LP muestra que encontrar la solución óptima está asociado con un punto de esquina. Este es el concepto básico cuando se desarrolla un método simplex.

Definición: Sea un sistema de m ecuaciones yn incógnitas (m <n). Dividimos las variables en dos conjuntos: (nm) establecemos las variables iguales a cero, y las m variables restantes se determinan resolviendo el sistema de ecuaciones iniciales. Si esta solución es única, las variables m distintas de cero se denominan básicas; cero (nm) variables: libre (no básico), y los valores resultantes correspondientes de las variables se denominan solución básica.

§4. Método simplex

El método simplex le permite encontrar efectivamente la solución óptima, evitando la enumeración simple de todos los puntos de esquina posibles. El principio principal del método: los cálculos comienzan con algún tipo de solución básica "inicial", y luego se realiza una búsqueda de soluciones que "mejoren" el valor de la función objetivo. Esto es posible solo si un aumento en alguna variable conduce a un aumento en el valor de lo funcional.

Requisitos previos para aplicar el método simplex:

1. La tarea debe tener una forma canónica.
2. La tarea debe tener una base explícita.

Definición: Una base seleccionada explícitamente es un vector de la forma:$$ $ en línea $ (.. 0100 ..) ^ T, (..010 ..) ^ T, (.. 0010 ..) ^ T ... $ en línea $ es decir solo una coordenada del vector es distinta de cero e igual a 1.

Nota: El vector base tiene dimensión (m * 1), donde m es el número de ecuaciones en el sistema de restricción.

Para conveniencia de los cálculos y la visualización, generalmente se usan tablas simplex:

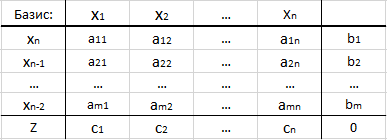
• La primera línea indica el "nombre" de todas las variables.
• En la primera columna, se indican los números de las variables base, y en la última celda, la letra Z (esta es la línea funcional).
• En el "centro de la tabla" indique los coeficientes de la matriz de restricción - aij.
• La última columna es el vector de los lados derechos de las ecuaciones correspondientes del sistema de restricción.
• La celda más a la derecha es el valor de la función objetivo. En la primera iteración, se supone que es 0.

Nota: Las bases son variables, coeficientes en la matriz de restricciones en las que se forman los vectores de base.

Nota: Si las restricciones en el problema original están representadas por desigualdades de la forma ≤, cuando el problema se reduce a la forma canónica, las variables adicionales introducidas forman la solución básica inicial.

Nota: Los coeficientes en la línea funcional se toman con el signo "-".

Algoritmo de método simplex:

1. Elija una variable que introduciremos en la base. Esto se hace de acuerdo con el principio indicado anteriormente: debemos elegir una variable cuyo aumento conduzca a un aumento en lo funcional. La selección se realiza de acuerdo con la siguiente regla:

• Si la tarea es mínima, seleccione el elemento positivo máximo en la última fila.
• Si la tarea está al máximo, seleccione el mínimo negativo.

Tal elección, de hecho, corresponde al principio mencionado anteriormente: si la tarea es mínima, cuanto mayor sea el número que restamos, más rápido disminuirá la funcionalidad; al máximo, por el contrario: cuanto mayor es el número, más rápido crece el funcional.

Nota: Aunque tomamos el número negativo mínimo en el problema al máximo, este coeficiente muestra la dirección de crecimiento de lo funcional, ya que la línea funcional en la tabla simplex se toma con el signo "-". Una situación similar con minimización.

Definición: Una columna de una tabla simplex correspondiente a un coeficiente seleccionado se denomina columna inicial.

2. Elija una variable que introduciremos en la base. Para hacer esto, debe determinar cuál de las variables base es más probable que desaparezca cuando la nueva variable base crece. Algebraicamente, esto se hace de la siguiente manera:

• El vector de las partes de la derecha se divide por la columna de terminación
• Entre los valores obtenidos, elija el mínimo positivo (no se consideran las respuestas negativas y cero)

Definición: Una línea de este tipo se llama línea inicial y corresponde a una variable derivada de la base.

Nota: De hecho, expresamos las viejas variables de base de cada ecuación del sistema de restricción a través del resto de las variables y vemos en qué ecuación el aumento en la nueva variable de base probablemente dará 0. Entrar en esta situación significa que nos topamos con un nuevo vértice. Por eso no se consideran los elementos cero y negativos, porque Obtener ese resultado significa que la elección de una variable base tan nueva nos alejará del área más allá de la cual no hay soluciones.

3. Estamos buscando un elemento de pie en la intersección de la fila y columna principal.

Definición: Tal elemento se llama elemento principal .

4. En lugar de la variable a excluir, en la primera columna (con los nombres de las variables básicas), escriba el nombre de la variable que ingresamos en la base.

5. Luego, comienza el proceso de cálculo de una nueva solución básica. Ocurre usando el método de Jordan-Gauss .

• Nueva línea de plomo = Antigua línea de plomo / plomo
• Nueva fila = Nueva fila - Factor de fila en la columna inicial * Nueva fila inicial

Nota: Una conversión de este tipo tiene como objetivo introducir la variable seleccionada en la base, es decir representación de la columna principal como vector base.

6. Después de eso, verificamos la condición de optimización. Si la solución resultante no es óptima, repita todo el proceso nuevamente.

§5. Interpretación del resultado del método simplex.

1. Óptima

La condición de optimización para la solución resultante:

• Si la tarea está al máximo, no hay coeficientes negativos en la fila funcional (es decir, con cualquier cambio en las variables, el valor del funcional resultante no crecerá).
• Si la tarea es mínima, no hay coeficientes positivos en la fila funcional (es decir, con cualquier cambio en las variables, el valor de la función resultante no disminuirá).

2. Funcionalidad ilimitada

Sin embargo, vale la pena señalar que un determinado funcional puede no alcanzar un máximo / mínimo en un área determinada. El atributo algebraico de esto se puede formular de la siguiente manera:

Al elegir una fila inicial (variable a excluir), el resultado de la división por términos del vector de los lados derechos por la columna inicial contiene solo valores cero y negativos.

De hecho, esto significa que no importa qué crecimiento establezcamos una nueva variable base, nunca encontraremos un nuevo vértice. Por lo tanto, nuestra función no se limita al conjunto de soluciones factibles.

3. Soluciones alternativas

Al encontrar la solución óptima, es posible otra opción: hay soluciones alternativas (otro punto de esquina que da el mismo valor de lo funcional).

Signo algebraico de la existencia de una alternativa:

Después de alcanzar la solución óptima, hay coeficientes cero para las variables libres en la fila funcional.

Esto significa que con el crecimiento de la variable correspondiente con un coeficiente cero, el valor de lo funcional no cambiará y una nueva solución básica también dará lo óptimo de lo funcional.

Epílogo

Este artículo está dirigido a una comprensión más profunda de la parte teórica. En los comentarios y explicaciones aquí puede obtener respuestas a preguntas que generalmente se omiten al estudiar este método y se toman a priori. Sin embargo, uno debe entender que muchos métodos de optimización numérica se basan en el método simplex (por ejemplo, el método Gomori , el método M ) y sin una comprensión fundamental, es poco probable que se pueda avanzar mucho en el estudio y la aplicación de todos los algoritmos de esta clase.

Un poco más adelante escribiré un artículo sobre la implementación práctica del método simplex, así como varios artículos sobre el Método de Variables Artificiales (Método M), el Método Gomori y el Método de Ramificación y Borde.

Gracias por su atencion!

PS

Si ya está atormentado por la implementación del método simplex, le aconsejo que lea el libro de A. Taha. Introducción al estudio de operaciones : todo está bien analizado allí, tanto en teoría como en ejemplos; y también vea ejemplos de resolución de problemas de matburo.ru; esto ayudará con la implementación en el código.