Libro de Alan Turing y Mysterious Note - Science Detective

Traducción original en mi blog

¿Cómo me llegó este libro?

En mayo de 2017, recibí un correo electrónico de mi antiguo maestro de secundaria llamado George Rutter, en el que escribió: “ Tengo una copia del gran libro alemán de Dirac (Die Prinzipien der Quantenmechanik), que perteneció a Alan Turing, y posteriormente mientras leía tu libro Idea Makers , me pareció por sentado que tú eres la persona que lo necesita ". Me explicó que había recibido un libro de otro (fallecido en ese momento) mi maestro de escuela Norman Rutledge , de quien sabía que era amigo de Alan Turing. George concluyó su carta con la frase: " Si necesita este libro, podría entregárselo la próxima vez que venga a Inglaterra ".

Después de un par de años en marzo de 2019, realmente llegué a Inglaterra, después de lo cual acordé con George encontrarnos para desayunar en un pequeño hotel en Oxford. Comimos, conversamos y esperamos a que la comida se asentara. Luego llegó el momento adecuado para discutir el libro. George metió la mano en su maletín y sacó un volumen académico típico y modestamente diseñado de mediados del siglo XX.



Abrí la portada, preguntándome si podría estar en el reverso de la inscripción: " Propiedad de Alan Turing" o algo así. Pero, desafortunadamente, este no fue el caso. Sin embargo, se le adjuntó una nota suficientemente expresiva en cuatro hojas de Norman Rutledge a George Rutter, escrita en 2002.

Conocí a Norman Rutledge cuando aún era un estudiante de secundaria en Eton a principios de la década de 1970. Era un profesor de matemáticas apodado The Nutty Norman. Fue un maestro agradable en todos los aspectos y contó un sinfín de historias sobre matemáticas y todo tipo de cosas interesantes. Fue responsable de garantizar que la escuela recibiera una computadora (programada con una cinta perforada del ancho de un escritorio); esta fue la primera computadora que utilicé .

En aquellos días, no sabía nada sobre el pasado de Norman (recuerde que esto fue mucho antes del advenimiento de Internet). Solo sabía que él era el "Dr. Rutledge". A menudo contaba historias sobre personas de Cambridge, pero en sus historias nunca mencionó a Alan Turing. Por supuesto, Turing no era lo suficientemente famoso en ese momento (aunque, según parece, ya supe de él por alguien que lo conocía en Bletchley Park (la mansión en la que se encontraba el centro de cifrado durante la Segunda Guerra Mundial)).

Alan Turing no fue famoso hasta 1981, cuando comencé a estudiar programas simples , aunque en aquel entonces en el contexto de autómatas celulares, y no en máquinas de Turing .

De repente, un día, mirando un catálogo de tarjetas en la biblioteca del Instituto de Tecnología de California , me topé con el libro Alan M. Turing , escrito por su madre Sarah Turing. El libro tenía mucha información, incluidos los trabajos científicos inéditos de Turing sobre biología. Sin embargo, no aprendí nada sobre su relación con Norman Rutledge, ya que el libro no mencionó nada sobre él (aunque, como descubrí, Sarah Turing se correspondió con Norman sobre este libro , y Norman incluso escribió una reseña al final).



Diez años más tarde, sintonizado con extrema curiosidad por Turing y su trabajo de biología (entonces inédito), visité el archivo de Turing en King's College, Cambridge . Pronto, habiéndome familiarizado con lo que tenían del trabajo de Turing, y después de dedicarle un tiempo, pensé que al mismo tiempo podría pedirle que también viera su correspondencia personal. Al revisarlo, encontré varias cartas de Alan Turing a Norman Rutledge.

En ese momento, se publicó la biografía de Andrew Hodges, que hizo tanto que Turing finalmente se hizo famoso, confirmó que Alan Turing y Norman Rutledge eran realmente amigos, y también que Turing era un consultor científico de Norman. Quería preguntarle a Rutledge sobre Turing, pero para entonces Norman ya estaba retirado y llevaba una vida aislada. Sin embargo, cuando completé el trabajo en el libro A New Kind of Science en 2002 (después de mi retiro de diez años), lo rastreé y le envié una copia del libro con el título "A mi último maestro de matemáticas". Luego nos correspondimos un poco, y en 2005 volví a Inglaterra y acepté reunirme con Norman para tomar una taza de té en un hotel de lujo en el centro de Londres.

Tuvimos una buena charla sobre muchas cosas, incluido Alan Turing. Norman comenzó nuestra conversación con la historia de que realmente conocía a Turing, sobre todo superficialmente, hace 50 años. Pero, sin embargo, tenía algo que contar sobre él personalmente: " Era insociable ". " Se rió mucho ". " Realmente no podía hablar con los no matemáticos ". " Siempre tuvo miedo de molestar a su madre ". " Se fue durante el día y corrió un maratón ". " No era demasiado ambicioso ". Entonces la conversación volvió a la identidad de Norman. Dijo que a pesar del hecho de que ya se había retirado durante 16 años, todavía escribe artículos para el " Periódico matemático ", de modo que, en sus palabras, "para completar todos sus trabajos científicos antes de ir a otro mundo " , donde, como agregó con una sonrisa apenas perceptible, " todas las verdades matemáticas ciertamente serán reveladas ". Cuando terminó la fiesta del té, Norman se puso su chaqueta de cuero y se dirigió a su ciclomotor, ignorando por completo las explosiones que interrumpieron el tráfico en Londres ese día.

Esta fue la última vez que vi a Norman, murió en 2013.

Seis años después, me senté a desayunar con George Rutter. Conmigo había una nota de Rutledge, escrita por él en 2002 con su letra característica:



Al principio leí la nota con fluidez. Ella era expresiva como siempre:

Recibí un libro de Alan Turing de su amigo y ejecutor Robin Gandy (en King's College era normal repartir libros de la colección de camaradas fallecidos, y elegí la colección de poemas de A.E. Houseman de los libros de Ivor Ramsey como un regalo adecuado (él era el decano y saltó de la capilla [en 1956]) ...

Más tarde, en una breve nota, escribe:

Usted pregunta dónde, al final, este libro debería haber ido; en mi opinión, debería ir a alguien que aprecia todo lo relacionado con el trabajo de Turing, por lo que su destino depende de usted.

Stephen Wolfram me envió su impresionante libro, pero no me sumergí lo suficiente en él ...

En conclusión, felicitó a George Rutter por tener el coraje de mudarse (como resultó, temporalmente) a Australia después de retirarse, y dijo que él mismo " jugaría mudarse a Sri Lanka como un ejemplo de una existencia barata y similar al loto ". pero agregó que "los eventos que tienen lugar allí ahora indican que no debería haber hecho esto " (aparentemente refiriéndose a la guerra civil en Sri Lanka).

Entonces, ¿qué se esconde en las entrañas del libro?

Entonces, ¿qué he hecho con una copia de un libro en alemán escrito por Paul Dirac que perteneció a Alan Turing? No leo alemán, pero tenía una copia del mismo libro en inglés (que es el idioma de su original) de la edición de 1970. Sin embargo, una vez en el desayuno me pareció correcto que debería revisar cuidadosamente el libro página por página. Al final, esta es una práctica común cuando se trata de libros antiguos.

Cabe señalar que me llamó la atención la elegancia de la presentación de Dirac. El libro fue publicado en 1931, pero su formalismo puro (y, sí, a pesar de la barrera del idioma, pude leer las matemáticas descritas en el libro) es casi lo mismo que si estuviera escrito hoy. (No quiero centrarme demasiado en Dirac aquí, pero mi amigo Richard Feynman me dijo que, al menos en su opinión, la exposición de Dirac es monosilábica. Norman Rutledge me dijo que era amigo en Cambridge del hijo adoptivo de Dirac , que se convirtió en teórico en Norman estaba muy a menudo en la casa de Dirac y dijo que el "gran hombre" a veces se desvanecía personalmente en el fondo, mientras que el primer plano siempre tenía muchos acertijos matemáticos. Desafortunadamente, yo nunca he conocido a Paul Dirac, aunque Me dijeron que después de t wow, cuando finalmente dejó Cambridge y se fue a Florida, perdió la mayor parte de su rigidez anterior y se convirtió en una persona bastante sociable).

Pero volvamos al libro de Dirac, que pertenecía a Turing. En la página 9, noté subrayados y pequeñas notas de margen escritas en lápiz simple. Seguí pasando las páginas. Después de varios capítulos, las notas desaparecieron. Pero luego, de repente, encontré una nota incrustada en la página 127 con el siguiente contenido:



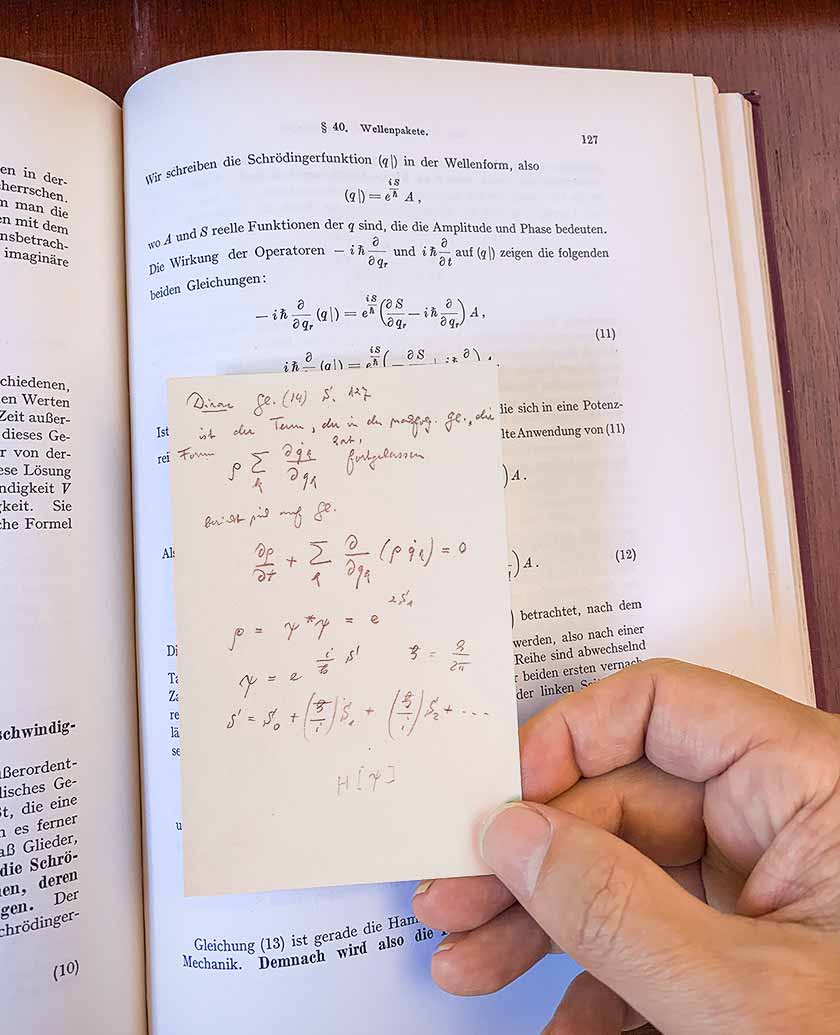
Fue escrito en alemán en letra alemana estándar. Y parece que de alguna manera podría estar conectado con la mecánica lagrangiana . Pensé que probablemente alguien poseía este libro antes de Turing, y esta debe ser una nota escrita por esta persona.

Seguí hojeando el libro. No hay notas Y pensé que ya no podía encontrar nada. Pero luego, en la página 231, encontré el marcador de la compañía, con texto impreso:



¿Eventualmente encontraré algo más? Seguí hojeando el libro. Luego, al final del libro, en la página 259, en la sección sobre la teoría relativista de los electrones, encontré lo siguiente:



Desplegué esta hoja de papel:



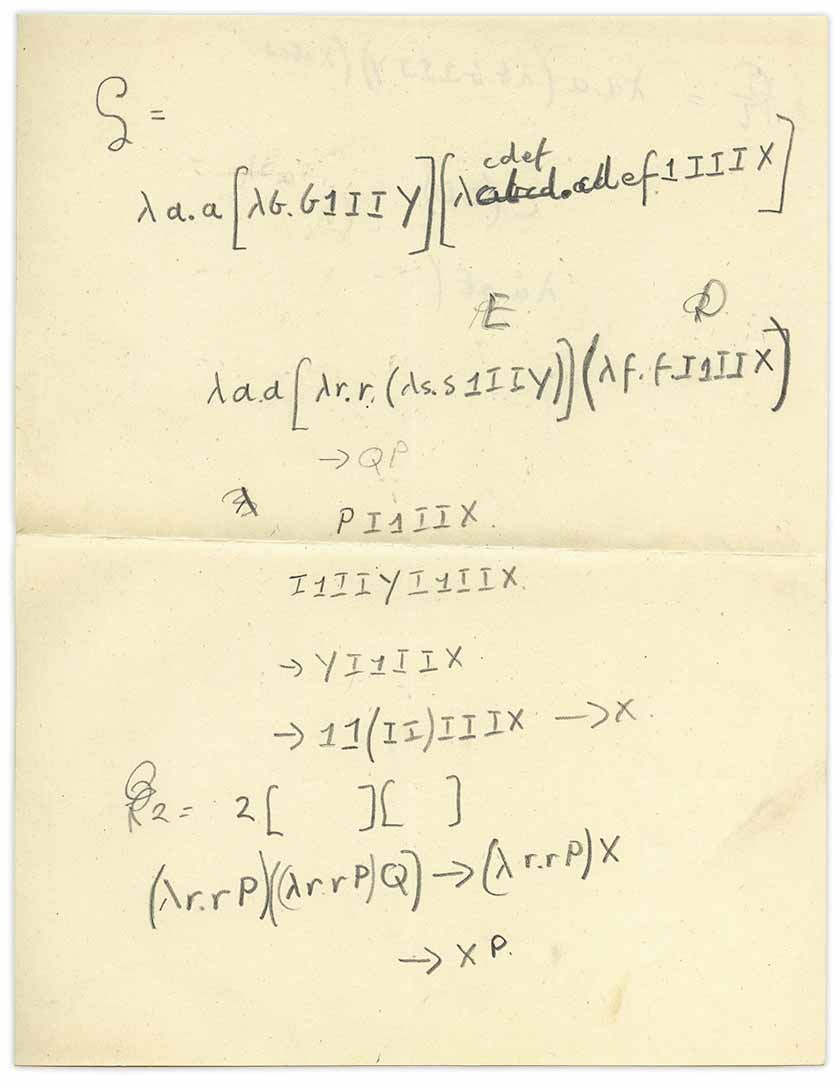
Inmediatamente me di cuenta de que se trataba de un cálculo lambda con una mezcla de combinadores , pero ¿cómo apareció esta hoja aquí? Recuerde que este libro es un libro sobre mecánica cuántica, pero la hoja adjunta trata de la lógica matemática, o lo que ahora se llama la teoría de la computación. Esto es típico de los escritos de Turing. Me preguntaba si Turing personalmente escribió esta nota.

Incluso durante el desayuno, busqué en Internet las muestras de escritura de Turing, pero no encontré ejemplos en forma de cálculos, por lo que no pude sacar conclusiones sobre la identidad exacta de la escritura. Y pronto tuve que irme. Empaqué cuidadosamente el libro, listo para revelar el secreto de lo que era la página y quién lo escribió, y lo llevé conmigo.

Sobre el libro

En primer lugar, discutamos el libro en sí. Los principios de la mecánica cuántica de Paul Dirac se publicaron en inglés en 1930 y pronto se tradujeron al alemán. (El prefacio de Dirac está fechado el 29 de mayo de 1930; pertenece al traductor Werner Bloch el 15 de agosto de 1930). El libro se convirtió en un hito en el desarrollo de la mecánica cuántica, estableciendo sistemáticamente un claro formalismo para realizar cálculos y, entre otras cosas, explicando la predicción de Dirac sobre el positrón , que será inaugurado en 1932.

¿Por qué Alan Turing tenía un libro en alemán, no en inglés? No lo sé con certeza, pero en aquellos días el alemán era el idioma principal de la ciencia, y sabemos que Alan Turing pudo leerlo. (Después de todo, en el título de su famoso trabajo de máquina de Turing " Acerca de los números computables con un apéndice al Problema de resolución (Entscheidungsproblem) "era una palabra alemana muy larga, y en la parte principal del artículo opera con caracteres góticos bastante oscuros en forma de" letras alemanas ", que usó en lugar de, por ejemplo, caracteres griegos).

¿Alan Turing compró el libro él mismo o se lo entregó? No lo se En el interior de la portada del libro de Turing hay una notación a lápiz "20 / -", que era la notación estándar "20 chelines", similar a £ 1. En la página de la derecha hay un "26.9.30" borrado, que supuestamente significa 26 de septiembre de 1930, tal vez la fecha en que se compró el libro por primera vez. Luego, en el extremo derecho, el número borrado es "20". Quizás este sea nuevamente el precio. (¿Podría ser este el precio en los Reichsmarks , si suponemos que el libro se vendió en Alemania? En ese momento, 1 Reichsmark valía aproximadamente 1 chelín, el precio alemán probablemente se escribiría como, por ejemplo, "20 RM"). Finalmente, en el interior de la contraportada es "c 5 / -", tal vez es (con un gran descuento) el precio de un libro usado.

Veamos las fechas principales de la vida de Alan Turing. Alan Turing nació el 23 de junio de 1912 (casualmente, exactamente 76 años antes de Mathematica 1.0 ). En el otoño de 1931, ingresó en King's College, Cambridge. Recibió su licenciatura después de los tres años estándar de estudio, en 1934.

En la década de 1920 y principios de la década de 1930, la mecánica cuántica era un tema candente, y Alan Turing estaba ciertamente interesado en él. Sabemos por sus archivos que en 1932, tan pronto como se publicó el libro, recibió los " Fundamentos matemáticos de la mecánica cuántica " de John von Neumann (en alemán ). También sabemos que en 1935 Turing recibió una tarea del físico de Cambridge Ralph Fowler sobre el tema del estudio de la mecánica cuántica. (Fowler propuso calcular la constante dieléctrica del agua , que en realidad es una tarea muy difícil, que requiere un análisis completo con la teoría de campo cuántico interactuante, que aún no está completamente resuelta).

Y sin embargo, ¿cuándo y cómo obtuvo Turing su copia del libro de Dirac? Dado que el libro tiene un precio roto, Turing supuestamente lo compró ya usado. ¿Quién fue el primer dueño del libro? Las notas en el libro parecen relacionarse principalmente con la estructura lógica, se observa que alguna relación lógica debe considerarse un axioma. Entonces, ¿qué pasa con la nota adjunta en la página 127?

Bueno, esto puede ser una coincidencia, pero solo en la página 127: Dirac habla sobre el principio cuántico de menor acción y sienta las bases para una integral a lo largo del camino de Feynman , que es la base de todo el formalismo cuántico moderno. ¿Qué contiene la nota? Contiene una extensión de la ecuación 14, que es una ecuación para la evolución temporal de la amplitud cuántica. El autor de la nota reemplazó Dirac A por amplitud con ρ, posiblemente reflejando el anterior registro alemán alemán (analogía de la densidad del líquido). Luego, el autor intenta expandir la acción en potencias de ℏ (la constante de Planck dividida por 2π, que a veces se denomina constante de Dirac ).

Pero parece que de lo que está contenido en la página, hay poco que se pueda aprender útil. Si mantiene la página a la luz, contiene una pequeña sorpresa: una marca de agua con la inscripción "Z f. Physik Chem B ":



Esta es una versión abreviada de Zeitschrift für physikalische Chemie, Abteilung B , la revista alemana de química física, que se ha publicado desde 1928. ¿Quizás la nota fue escrita por el editor de la revista? Aquí está el título de la revista para 1933. Convenientemente, los editores se enumeran con su ubicación, y uno de ellos se destaca: "Born · Cambridge".



Este es Max Bourne, autor de la regla de Bourne y mucho más en la teoría de la mecánica cuántica (así como el abuelo de la cantante Olivia Newton-John ). Entonces, ¿esta nota puede haber sido escrita por Max Born? Pero, desafortunadamente, esto no es así, porque la letra no coincide.

¿Qué pasa con los marcadores en la página 231? Aquí es de dos lados:



El marcador es raro y bastante bonito. ¿Pero cuándo se hizo? Hay una librería Heffers en Cambridge , aunque ahora es parte de Blackwell. Durante más de 70 años (hasta 1970), Heffers se ubicó en la dirección, como muestra la pestaña, 3 y 4 por Petty Cury .

Esta pestaña contiene una clave importante: este es el número de teléfono „Tel. 862. " Resultó que en 1939 la mayor parte de Cambridge (incluyendo Heffers) cambió a números de cuatro dígitos y, por supuesto, en 1940 los marcadores se imprimieron con números de teléfono "modernos". (Los números telefónicos en inglés gradualmente se hicieron más largos; cuando crecí en Inglaterra en la década de 1960, nuestros números telefónicos eran Oxford 56186 y Kidmore End 2378. En parte, recuerdo estos números porque, curiosamente, ahora es no se veía, siempre llamaba a mi número cuando contestaba una llamada entrante).

El marcador en este formulario se imprimió hasta 1939. ¿Pero cuánto tiempo antes de eso? Puede encontrar bastantes escaneos de anuncios antiguos de Heffers en Internet, al menos desde 1912 (junto con "Le pedimos que satisfaga sus solicitudes ...") agregan "Teléfono 862", agregando "(2 líneas)". También hay algunos marcadores con un diseño similar que se pueden encontrar en los libros desde 1904 (aunque no está claro si fueron originales para estos libros (es decir, impresos al mismo tiempo). A los fines de nuestra investigación, parece que podemos concluir que Este libro vino de la tienda Heffers (que, por cierto, era la librería principal de Cambridge) en algún momento entre 1930 y 1939.

Página con cálculo lambda

Así que ahora sabemos algo sobre cuándo se compró el libro. Pero, ¿qué pasa con la "página de cálculo lambda"? ¿Cuándo se escribió esto? Bueno, por supuesto, para entonces, el cálculo lambda debería haberse inventado. Y esto fue hecho por Alonzo Church , un matemático de Princeton , en su forma original en 1932 y en su forma final en 1935. (Hubo trabajos de científicos de predecesores, pero no utilizaron la notación λ).

Existe una relación compleja entre Alan Turing y el cálculo lambda. En 1935, Turing se interesó en la "mecanización" de las operaciones matemáticas e inventó la idea de una máquina de Turing que la utilizara para resolver los problemas de los fundamentos de las matemáticas. Turing envió un artículo sobre este tema a la revista francesa ( Comptes rendus ), pero se perdió en el correo; y luego resultó que el destinatario a quien la envió todavía no estaba allí, ya que se había mudado a China.

Pero en mayo de 1936, incluso antes de que Turing pudiera enviar su artículo a otra parte, el trabajo de Alonzo Church llegó de los Estados Unidos . , 1934 , , , 1922 .
, - , ( - ). ( ) , , . 1936 ( ) « …» .

: 1936 1938 ( 1937 ) , , . , -, — , - , — , , .

1938 , , -, , . 1945 , . 1947–8 , , .

1951 . ( , , , , - , ). , 1954 , : « » ( : « , »). , , 7 1954 , . ( , , .)

, -. , :



, , , . ? , , , Spalding&Hodge, Papermakers, « », - , -, . , , , Excelsior, , 1890- 1954 .

?

Entonces, echemos un vistazo más de cerca a lo que está a ambos lados de la hoja. Comencemos con lambdas.

Aquí hay una manera de definir funciones "puras" o "anónimas" , y son el concepto básico en lógica matemática, y ahora en programación funcional. Estas funciones son bastante comunes en Wolfram Language , y su trabajo es bastante fácil de explicar. Por ejemplo, alguien escribe f [ x ] para denotar la función f aplicada al argumento x. Y hay muchas funciones con nombre f como Abs o Sin o Blur . Pero, ¿qué pasa si alguien quiere que f [ x ] sea 2x +1 ? No hay un nombre inmediato para esta función. Pero, ¿hay otra forma de asignación, f [ x ]?

La respuesta es sí: en lugar de f escribimos la Function[a,2a+1] . Y en el lenguaje de Function [a,2a+1][x] Wolfram Function [a,2a+1][x] aplica funciones al argumento x, dando como resultado 2x+1 . Function[a,2a+1] es una función "pura" o "anónima", que es una operación pura de multiplicar por 2 y sumar 1.

Entonces, λ en el cálculo lambda es un análogo exacto de Function en Wolfram Language, y por lo tanto, λ a. (2 a + 1) es equivalente a Function[a, 2a + 1] . (Vale la pena señalar que la función, por ejemplo, Function[b,2b+1] equivalente; las "variables relacionadas" aob son solo lugares para sustituir el argumento de la función, y en Wolfram Language se pueden evitar usando opciones alternativas para definir una función pura (2# +1)& ).

En las matemáticas tradicionales, las funciones generalmente se consideran objetos que muestran datos de entrada (por ejemplo, enteros) y datos de salida (que también son, por ejemplo, enteros). Pero, ¿qué es este objeto Function (o λ)? En esencia, este es un operador estructural que toma expresiones y las convierte en funciones. Esto puede parecer un poco extraño en términos de las matemáticas tradicionales y la forma matemática de escribir, pero si alguien necesita manipular caracteres arbitrarios, lo cual es mucho más natural, incluso si al principio parece un poco abstracto. (Cabe señalar que cuando los usuarios aprenden Wolfram Language, siempre puedo decir que han superado un cierto umbral de pensamiento abstracto cuando tienen una idea de Function ).

Las lambdas son solo parte de lo que hay en la página. Existe otro concepto aún más abstracto: estos son los combinadores . Considere la línea PI1IIx bastante oscura? ¿Qué significa eso? De hecho, esta es una secuencia de combinadores, o, una composición abstracta de funciones simbólicas.

La superposición habitual de funciones, bastante familiar en matemáticas, en Wolfram Language se puede escribir en la forma: f[g[x]] - que significa "aplicar f al resultado de aplicar g a x ". ¿Pero son realmente necesarios los soportes para esto? En Wolfram, f@g@ x es una forma alternativa de notación. En esta publicación, confiamos en la definición de Wolfram Language: el operador @ está asociado con el lado derecho, por lo que f@g@x equivalente a f@(g@x) .

Pero, ¿qué significará la entrada (f@g)@x ? Esto es equivalente a f[g][x] . Y si fyg fueran funciones ordinarias en matemáticas, eso no tendría sentido, pero si f es una función de orden superior , entonces f[g] sí misma puede ser una función que se puede aplicar muy bien a x .

Tenga en cuenta que todavía hay cierta complejidad. En f[] - f es una función de un argumento. Y f[] equivalente a escribir la Function[a, f[a]][x] . Pero, ¿qué pasa con la función de dos argumentos, por ejemplo, f[x,y] ? Esto se puede escribir como Function[{a,b},f[a, b]][x, y] . Pero, ¿qué pasa con la Function[{a},f[a,b]] ? Que es esto Hay una "variable libre" b , que simplemente se pasa a la función. Function[{b},Function[{a},f[a,b]]] unirá esta variable, y luego la Function[{b},Function[{a},f [a, b]]][y][x] da f[x,y] nuevo. (Establecer la función para que tenga un argumento se llama "curry" en honor del científico lógico llamado Haskell Curry ).

Si existen variables libres, es decir, hay muchas dificultades diferentes con respecto a cómo se pueden definir las funciones, pero si nos restringimos a objetos Function u λ que no tienen variables libres, entonces básicamente se pueden establecer libremente. Tales objetos se llaman combinadores.

Los combinadores tienen una larga historia. Se sabe que fueron propuestos por primera vez en 1920 por el discípulo de David Gilbert , Moses Schoenfinkel .

En ese momento, solo muy recientemente se descubrió que no era necesario usar las expresiones And , Or y Not para representar expresiones en la lógica proposicional estándar: era suficiente usar el único operador, que ahora llamaremos Nand (porque, por ejemplo, si escribimos Nand ·, Entonces Or[a,b] toma la forma (a · a) · (b · b) ). Schönfinkel quería encontrar la misma representación mínima de lógica de predicados, o esencialmente lógica, incluidas las funciones.

Se le ocurrieron dos "combinadores" S y K. En Wolfram Language, esto se escribe como
K [x _] [y_] → x y S [x _] [y _] [z_] → x [z] [y [z]].

Es de destacar que fue posible utilizar estos dos combinadores para realizar cualquier cálculo. Entonces por ejemplo

S [K [S]] [S [K [S [K [S]]]]] [S [K [K]]]]

se puede usar como una función para agregar dos enteros.

Todos estos, por decirlo suavemente, son objetos bastante abstractos, pero ahora que entendemos qué son las máquinas de Turing y el cálculo lambda, podemos ver que los combinadores de Schoenfinkel realmente anticiparon el concepto de computación universal. (Y aún más notable, las definiciones de S y K de 1920 son mínimamente simples y se parecen a la máquina de Turing universal muy simple que propuse en la década de 1990, cuya universalidad se demostró en 2007 ).

Pero volvamos a nuestro folleto y línea PI1IIx . Los caracteres grabados aquí son combinadores, y todos están diseñados para definir una función. Aquí la definición es que la superposición de funciones debe ser asociativa a la izquierda, por lo que fgx no debe interpretarse como f @ g @ x o f @ (g @ x) o f [g [x]], sino como (f @ g ) @x o f [g] [x]. Traduciremos esta entrada a un formato conveniente para Wolfram Language: PI1IIx tomará la forma p [i] [one] [i] [i] [x] .

¿Por qué escribir algo así? Para explicar esto, necesitamos discutir el concepto de números de la Iglesia (llamado así por la Iglesia Alonzo). Digamos que solo trabajamos con símbolos y con lambdas o combinadores. ¿Hay alguna manera de usarlos para especificar enteros?

¿Qué tal simplemente decir que el número n corresponde a la Function[x, Nest[f,x,n]] ? O, en otras palabras, eso (en notación más corta):

1 es f[#]&
2 es f[f[#]]&
3 es f[f[f[#]]]& y así sucesivamente.

Todo esto puede parecer algo más oscuro, pero la razón por la que es interesante es que nos permite hacer todo completamente simbólico y abstracto, sin tener que hablar explícitamente de algo como números enteros.

Con este método de especificar números, imagine, por ejemplo, sumar dos números: 3 puede representarse como f[f[f[#]]]& y 2 es f[f[#]]& . Puede agregarlos simplemente aplicando uno de ellos al otro:



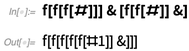
¿Pero cómo es f ? ¡Podría ser cualquier cosa! En cierto sentido, "ir a lambda" hasta el final y representar números usando funciones que toman f como argumento. En otras palabras, imagine 3, por ejemplo, como Function[f,f[f[f[#]]] &] o Function[f,Function[x,f[f[f[x]]]] . (cuándo y cómo necesita nombrar variables es una trampa en el cálculo lambda).

Considere un fragmento del artículo de Turing de 1937, Computabilidad y Difusibilidad λ , que configura los objetos exactamente como acabamos de discutir:



Aquí, la grabación puede ser algo confusa. La x de Turing es nuestra f , y su x ' (el compositor cometió un error al insertar un espacio) es nuestra x . Pero aquí se usa exactamente el mismo enfoque.

Entonces, veamos la línea inmediatamente después del doblez frente a la hoja. Esto es I1IIYI1IIx . Según la forma de Wolfram Language, este será i[one][i][i][y][i][one][i][i][x] . Pero aquí i es una función idéntica, por lo tanto, i[one] devuelve solo una . Mientras tanto, uno es la representación numérica de Church para 1 o Function[f,f[#]&] . Pero con esta definición, one[] convierte a[#]& y one[a][b] convierte a[b] . (Por cierto, i[][b] , o Identity[][b] también Identity[][b] a [b] ).

Será mucho más claro si escribimos las reglas de reemplazo para i y one , en lugar de usar directamente el cálculo lambda. El resultado será el mismo. Aplica estas reglas explícitamente, obtenemos:



Y esto es exactamente lo mismo que se presenta en el primer registro abreviado:



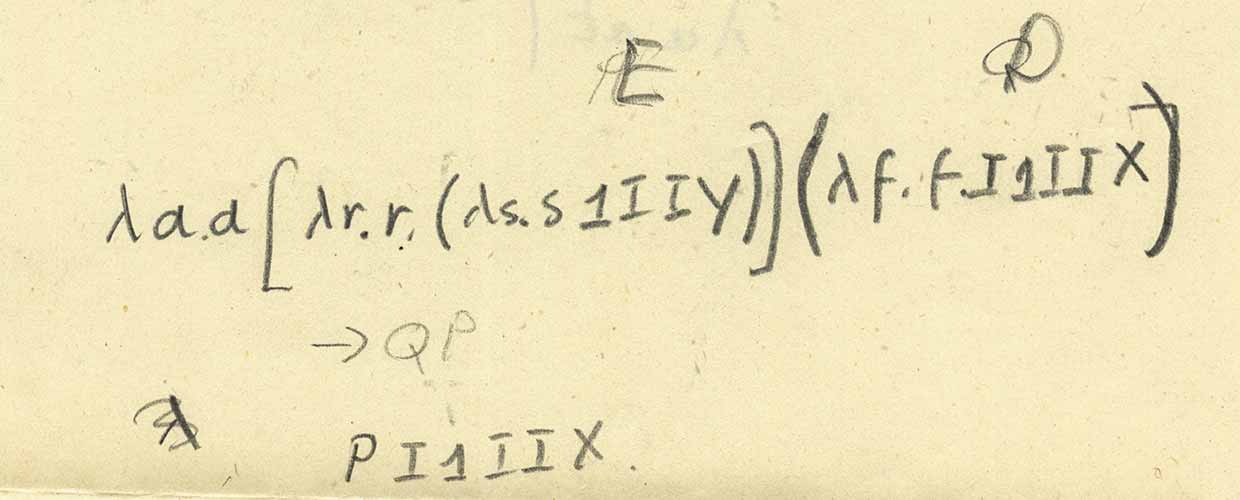
Miremos ahora la hoja nuevamente, en su parte superior:



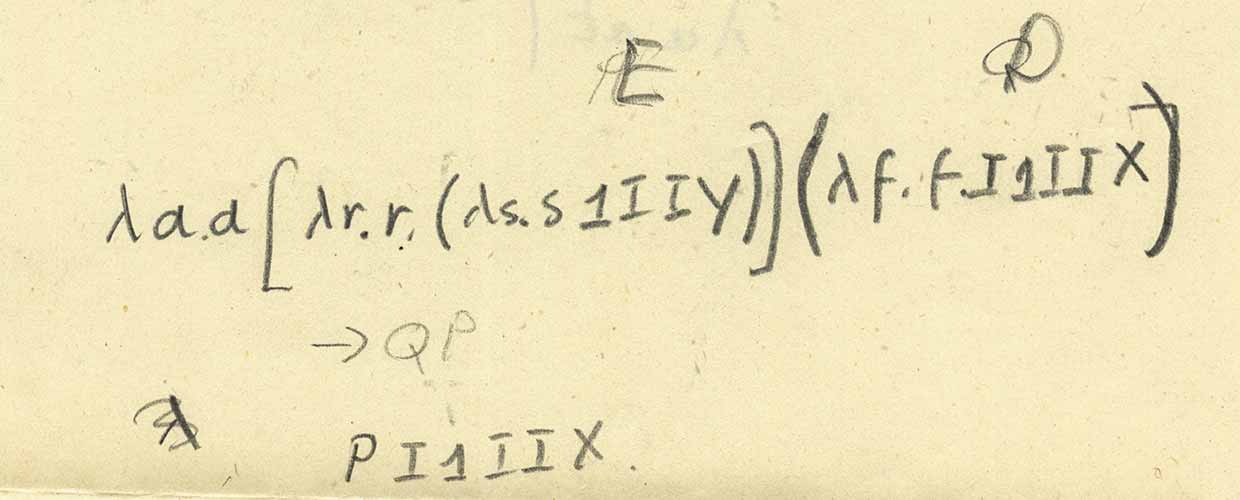
Hay objetos bastante confusos e incomprensibles "E" y "D", pero con ellos queremos decir "P" y "Q", por lo que podemos escribir la expresión y calcularla (tenga en cuenta que aquí, después de cierta confusión con el último símbolo - "científico misterioso" pone [...] y (...) para representar las funciones de la aplicación):



Entonces esta es la primera abreviatura que se muestra. Para ver más, sustituyamos las definiciones por Q:



Obtenemos exactamente la siguiente abreviatura que se muestra. ¿Qué sucede si sustituimos las expresiones por P?



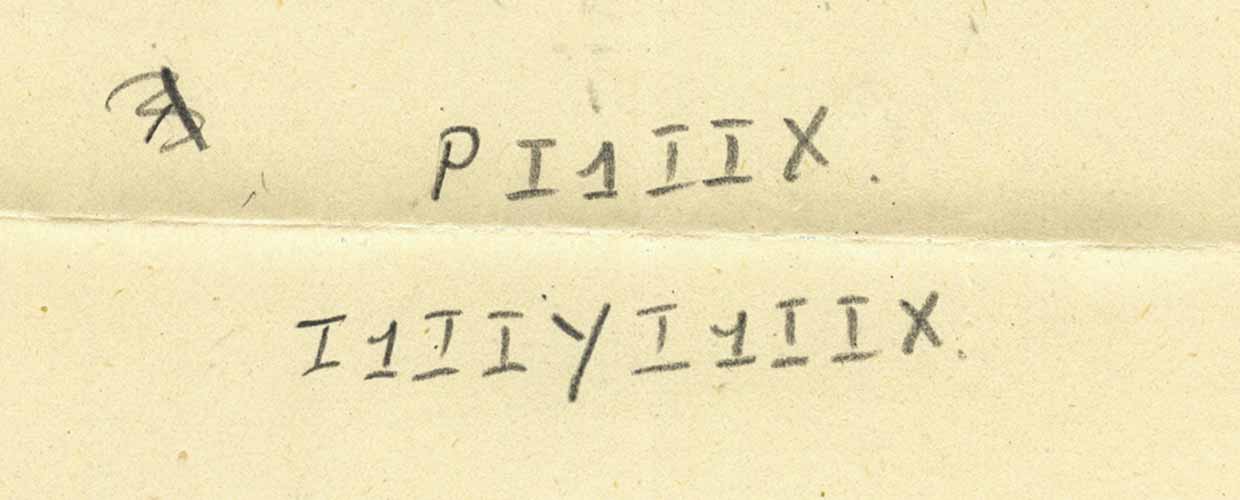
Aquí está el resultado:



Y ahora, usando el hecho de que i es una función que genera el argumento en sí, obtenemos:



Oooops! Pero esta no es la siguiente línea registrada. ¿Hay algún error aquí? No está claro Porque, al final, a diferencia de la mayoría de los otros casos, no hay una flecha que indique que la siguiente línea sigue a la anterior.

Aquí hay algún tipo de misterio, pero pasemos al final del folleto:



Aquí 2 es el número de la Iglesia, definido, por ejemplo, por el patrón two[a_] [b_] → a[a[b]] . Tenga en cuenta que esta es en realidad la forma de la segunda línea si a se trata como Function[r,r[]] yb como q . Entonces, esperamos que el resultado de los cálculos sea el siguiente:



Sin embargo, la expresión [b] encuentra dentro puede escribirse como x (probablemente difiere de x escrita previamente en la hoja) - como resultado, obtenemos el resultado final:



Entonces, podemos descifrar un poco de lo que está sucediendo en esta hoja, pero al menos un enigma que aún permanece es lo que debería ser Y.

De hecho, la lógica combinatoria tiene un combinador Y estándar: el llamado combinador de punto fijo . Formalmente, se define por el hecho de que Y [ f ] debe ser igual a f [Y [ f ]], o, en otras palabras, Y [ f ] no cambia cuando se aplica f, por lo que este es un punto fijo para f . (El combinador Y está asociado con el # 0 en Wolfram Language).

Actualmente, el Y-combinator se ha hecho famoso gracias al acelerador de lanzamiento Y-Combinator , llamado Paul Graham (que durante mucho tiempo fue fanático de la programación funcional y del lenguaje de programación LISP e implementó la primera tienda web basada en este lenguaje). Una vez me dijo personalmente, " nadie entiende lo que Y es un combinador ". (Cabe señalar que Y Combinator es exactamente lo que permite a las empresas evitar operaciones de punto fijo ...)

El combinador Y (como un combinador de punto fijo) se inventó varias veces. A Turing realmente se le ocurrió su implementación en 1937, a la que llamó Θ. Pero, ¿es la letra "Y" en nuestra página un famoso combinador de punto fijo? Quizás no. Entonces, ¿cuál es nuestra "Y"? Considere esta reducción:



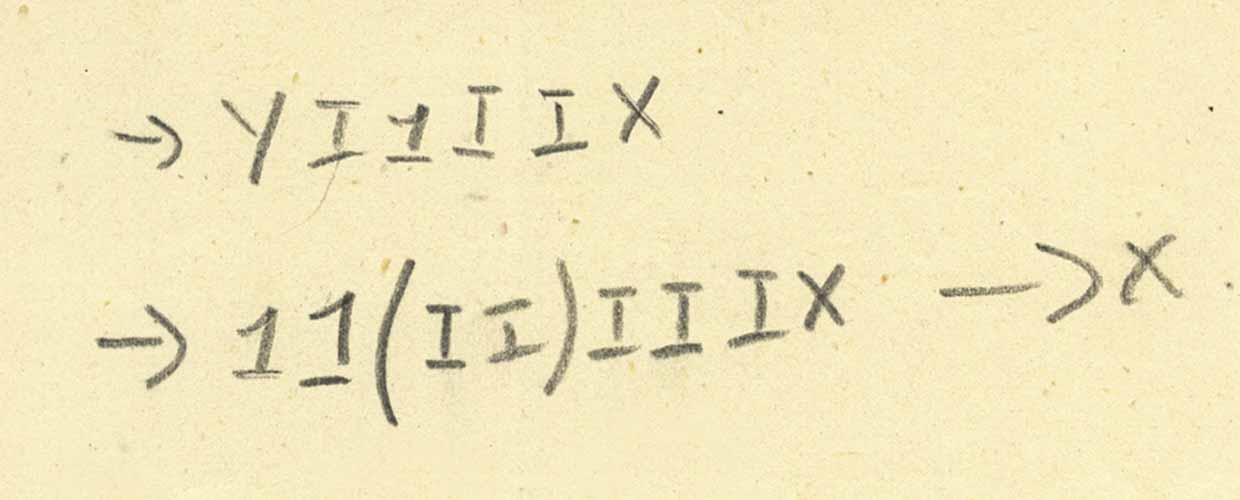
Pero esta información claramente no es suficiente para determinar inequívocamente qué es Y. Está claro que Y opera no solo con un argumento; Parece que el asunto es al menos dos argumentos, pero no está claro (al menos para mí) cuántos argumentos se necesitan para la entrada y qué hace.

Finalmente, aunque podemos dar sentido a muchas partes del folleto, debemos decir que a escala global no está claro qué se hizo en él. Aunque requiere muchas explicaciones de lo que se presenta en la hoja, es bastante elemental en el cálculo lambda y el uso de combinadores.

Presumiblemente, aquí hay un intento de crear un "programa" simple: usar el cálculo lambda y los combinadores para hacer algo. Pero en la medida en que esto es típico para la ingeniería inversa, es difícil para nosotros decir qué debería ser este "algo" y cuál es un objetivo común "explicable".

Hay otra característica presentada en la hoja, que vale la pena comentar aquí: el uso de varios tipos de corchetes. En matemática tradicional, los paréntesis se usan principalmente para todo, y aplicaciones de una función (como en f (x) ), y agrupaciones de miembros (como en (1 + x) (1-x) , o, menos obviamente, a (1- x) ). (En Wolfram Language, separamos los diversos usos de los corchetes, entre corchetes para definir las funciones f [x] , y los paréntesis se usan solo para la agrupación).

Cuando apareció por primera vez el cálculo lambda, había muchas preguntas sobre el uso de corchetes. Más tarde, Alan Turing escribió un trabajo completo (inédito) titulado " Transformando la forma matemática de notación y fraseología ", pero ya en 1937 sintió que necesitaba describir definiciones modernas (en lugar de piratas informáticos) para el cálculo lambda (que, por cierto, surgió de para la iglesia).

Dijo que f aplicado a g debería escribirse {f} (g) , a menos que f sea ​​el único carácter, en cuyo caso podría ser f (g) . Luego dijo que lambda (como en la Function[a, b] ) debería escribirse como λ a [ b ] o, alternativamente, λ a . b .

Sin embargo, quizás en 1940 se descartó la idea de utilizar {...} y [...] para denotar diferentes objetos, principalmente a favor de los corchetes en un estilo matemático estándar.

Echa un vistazo a la parte superior de la página:



De esta forma, es difícil de entender. En las definiciones de la Iglesia, los corchetes son para agrupar, con un corchete de apertura que reemplaza un punto. Usando esta definición, queda claro que Q (eventualmente etiquetado como D), encerrado entre paréntesis al final, es a lo que se aplica toda la lambda inicial.

De hecho, el corchete aquí no limita el cuerpo de la lambda; en cambio, en realidad representa otra aplicación de la función, y no hay una indicación explícita de dónde termina el cuerpo lambda. Al final, está claro que el "científico misterioso" cambió el corchete de cierre a uno redondo, aplicando así efectivamente la definición de Church y obligándolo a calcular la expresión, como se muestra en la hoja.

Entonces, ¿qué significa esta pequeña pieza de todos modos? Creo que esto sugiere que la página se escribió en la década de 1930, o no mucho después, ya que la leyenda de los corchetes aún no se había establecido.

Entonces, ¿de quién era la letra?

Entonces, antes de eso hablamos sobre lo que está escrito en la página. ¿Pero qué pasa con el que lo escribió de todos modos?

El candidato más obvio para este papel sería el propio Alan Turing, ya que, después de todo, la página estaba dentro de su libro. En términos de contenido, parece que no hay nada incompatible con el hecho de que Alan Turing podría escribir esto, incluso en el momento en que comenzó a lidiar con el cálculo lambda después de recibir el artículo de Church a principios de 1936.

¿Qué hay de la escritura a mano? ¿Pertenece a Alan Turing? Considere varias muestras sobrevivientes, que, como sabemos con certeza, fueron escritas por Alan Turing:



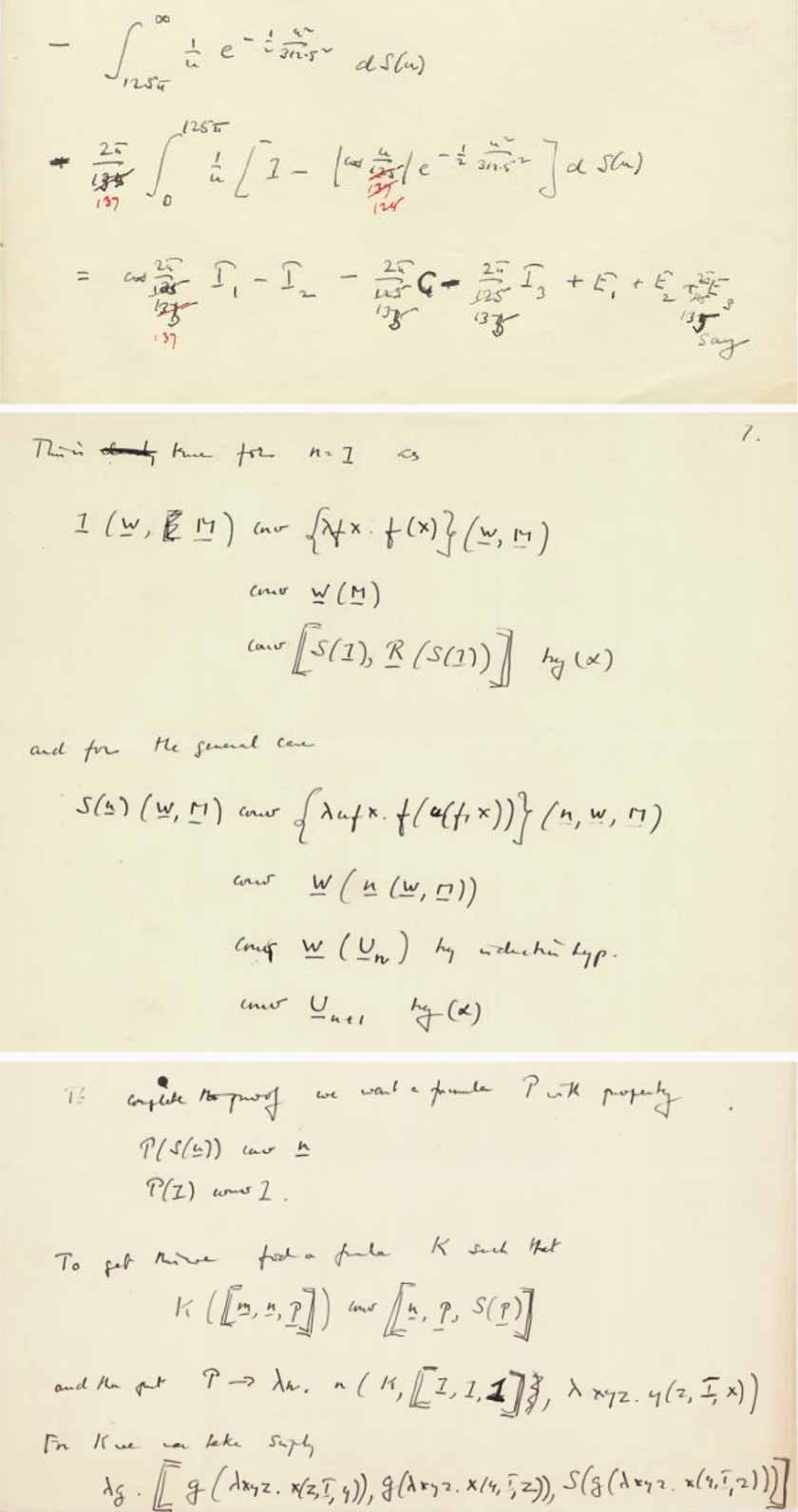
El texto presentado claramente se ve muy diferente, pero ¿qué pasa con la notación utilizada en el texto? Al menos, en mi opinión, esto no parece tan obvio, y podemos suponer que cualquier diferencia puede ser causada por el hecho de que las muestras existentes (presentadas en los archivos) están escritas, por así decirlo, "al final", mientras que las nuestras Una página es un reflejo del trabajo del pensamiento.

Resultó conveniente para nuestra investigación que había una página en el archivo de Turing en la que escribió una tabla de caracteres necesarios para la anotación. Y al comparar estos caracteres letra por letra, se parecen bastante a mí (estos registros se hicieron durante el tiempo de Turing cuando estudiaba el crecimiento de las plantas , por lo tanto, apareció la nota "área de la hoja"):



Quería investigar esto más a fondo, así que envié muestras a Sheila Lowe , una experta profesional en escritura (y autora de escritura), a quien conocí una vez, simplemente presentando nuestro folleto como "muestra A" y la escritura existente de Turing como "Muestra" B ". Su respuesta fue final y negativa: “ El estilo de escritura es completamente diferente. En cuanto a la personalidad, el autor de la muestra "B" tiene una forma de pensar más rápida e intuitiva que el autor de la muestra "A ".

Todavía no estaba completamente convencido de esto, pero decidí que era hora de buscar otras opciones.

Entonces, si resulta que Turing no escribió esto, ¿quién lo hizo? Norman Rutledge me dijo que recibió el libro de Robin Gandhi, quien era el albacea de Turing. Entonces envié "Muestra" C "" de Gandhi:



Pero la conclusión inicial de Sheila fue que las tres muestras probablemente fueron escritas por tres personas diferentes, y nuevamente señaló que la muestra "B" se obtuvo del " pensador más rápido, el que probablemente busca soluciones inusuales a los problemas ". . (Encuentro agradable que un especialista en escritura moderna hiciera tal evaluación de la escritura de Turing, dado lo activamente que todos en las tareas escolares de Turing de la década de 1920 se quejaron de su escritura).

Bueno, en ese momento, parecía que tanto Turing como Gandhi estaban excluidos de la lista de "sospechosos". Entonces, ¿quién podría escribir esto? Empecé a pensar en personas a quienes Turing podía prestarle su libro. Por supuesto, al mismo tiempo, deberían poder hacer cálculos utilizando el cálculo lambda.

Sugerí que la persona debería ser de Cambridge, o al menos de Inglaterra, dada la marca de agua en papel. Confundí la hipótesis de trabajo de que 1936 más o menos era el momento adecuado para escribir esto. Entonces, ¿a quién conocía en ese momento y con quién se comunicaba Turing? . ( 13 , 1930 1936 .)

. , , , — 1933 , («» ) : 0.12345678910111213… ( 1, 2, 3, 4 ,…, 8, 9, 10, 11, 12,…, , «» , ).

1937 - , , . ( , - ).

, ( ) , . ( , 1948 Turbochamp — , , ).

? LinkedIn, , , Microsoft. , , . ( ):



, ( f . .)

? , . « », , . ( , , , , , ).

— , .

«»

, . , , , , , .

, -, ? 1946 (, ). 1949 , . 1954 , . , 1957 . , (, , , , . .). 1960 , ( ) ( ), , .

? - (, , , 2005 , «»). , « ».

- , , , ? . , - - - . , 1955 « » ( , BooleanMinimize ). , ( «NAR», «NAR…», , «NARLAB» — «» ). .

. , , , « ». , , , , 1954 , . , , .

, « ( , ) » « , , , , [ ] ». , ? . ( , , , 1902 , « » : « »).

, , , , , 12 , -, , , 21 ).

, , - . , - . , , , 1938 . 2000 - ( ) — , , 2002 , .

, , ? , , . :



, . , , , , , .

: ? , , , .

- , — 1940 — . , 1944 , , . , , .

, , , , 1952 , « » . , , , , — , , . , . , , , , . , 1980- , “ » — , , , . ( , , , , « , »). , « , , , — … », , « ».)

, , . . , « » (. . -), -.

. 1969 , , , , , .
, , . . — — . . - , , .

1995 , . — . . , , — , , , . , , , , , 24 . ( 2001 — 45 ).

, ? , , , , , ( , , , c ). ( ) « » ( ), , -, , . , .

, . , 30 , . , , , - — , , , (, , , Mathematica ). , , , , , , , . , , , .

? , , () , . ( , .) , 1 . , .

, , . : « ! » , . . , -, , , .

, , , , , . , : . ; .

, . , ? - , 1930- . , , , - 1940- . , . , , , , , -.

, - , , , . , , , , , , . , , — , , …

: ( ), ( ) ( ).

Wolfram Language?
.
Inscripción para nuevos cursos . Curso en línea listo.
Wolfram Language.