Resolver la ecuación de regresión lineal simple.

El artículo analiza varios métodos para determinar la ecuación matemática de una línea de regresión simple (por pares).

Todos los métodos para resolver la ecuación discutida aquí se basan en el método de mínimos cuadrados. Denotamos los métodos de la siguiente manera:

• Solución analítica
• Descenso de gradiente
• Descenso de gradiente estocástico

Para cada uno de los métodos para resolver la ecuación de la línea recta, el artículo describe varias funciones que se dividen principalmente en las que se escriben sin usar la biblioteca NumPy y las que usan NumPy para los cálculos. Se cree que el uso hábil de NumPy reduce los costos informáticos.

Todo el código en este artículo está escrito en python 2.7 usando el Jupyter Notebook . Código fuente y archivo de datos de muestra publicado en github

El artículo está más enfocado tanto en principiantes como en aquellos que ya han comenzado a dominar el estudio de una sección muy extensa en inteligencia artificial: el aprendizaje automático.

Para ilustrar el material, usamos un ejemplo muy simple.

Condiciones de ejemplo

Tenemos cinco valores que caracterizan la dependencia de Y en X (Tabla No. 1):

Tabla No. 1 "Condiciones del ejemplo"



Suponemos que los valores $$$x_i$ Es el mes del año y $$$y_i$ - Ingresos de este mes. En otras palabras, los ingresos dependen del mes del año, y $$$x_i$ - El único signo del que dependen los ingresos.

Un ejemplo es regular, tanto en términos de la dependencia condicional de los ingresos en el mes del año, como en términos de la cantidad de valores; hay muy pocos de ellos. Sin embargo, esta simplificación permitirá que lo que se llama en los dedos explique, no siempre con facilidad, el material absorbido por los principiantes. Y también la simplicidad de los números permitirá, sin costos laborales significativos, a aquellos que deseen resolver el ejemplo en papel.

Suponga que la dependencia que se muestra en el ejemplo puede aproximarse bastante bien mediante la ecuación matemática de una línea de regresión simple (por pares) de la forma:

$$

$$Y = a + bx$$

donde $$$x$ - este es el mes en que se recibieron los ingresos, $$$Y$ - ingresos correspondientes al mes, $$$a$ y $$$b$ - coeficientes de regresión de la línea estimada.

Tenga en cuenta que el coeficiente $$$b$ a menudo llamado pendiente o gradiente de la línea estimada; representa la cantidad por la cual cambiar $$$Y$ al cambiar $$$x$ .

Obviamente, nuestra tarea en el ejemplo es seleccionar dichos coeficientes en la ecuación $$$a$ y $$$b$ para lo cual las desviaciones de nuestros ingresos mensuales estimados de las respuestas verdaderas, es decir Los valores presentados en la muestra serán mínimos.

Método de mínimos cuadrados

De acuerdo con el método de mínimos cuadrados, la desviación debe calcularse cuadrándola. Tal técnica evita el reembolso mutuo de las desviaciones, si tienen signos opuestos. Por ejemplo, si en un caso, la desviación es +5 (más cinco) y en el otro -5 (menos cinco), la suma de las desviaciones se reembolsará mutuamente y será 0 (cero). No puede desperdiciar la desviación, pero use la propiedad del módulo y luego todas las desviaciones serán positivas y se acumularán en nosotros. No nos detendremos en este punto en detalle, sino que simplemente indicaremos que para la conveniencia de los cálculos, es costumbre ajustar la desviación al cuadrado.

Así es como se ve la fórmula con la ayuda de la cual determinamos la suma más pequeña de desviaciones al cuadrado (errores):

$$

$$ERR (x) = \ sum \ limits_ {i = 1} ^ n (a + bx_i - y_i) ^ 2 = \ sum \ limits_ {i = 1} ^ n (f (x_i) -y_i) ^ 2 \ rightarrow min$$

donde $$$f (x_i) = a + bx_i$ Es una función de aproximación de respuestas verdaderas (es decir, ingresos calculados por nosotros),

$$$y_i$ - estas son respuestas verdaderas (ingresos provistos en la muestra),

$$$i$ Es el índice de muestra (el número del mes en el que se determina la desviación)

Diferenciamos la función, definimos las ecuaciones diferenciales parciales y estamos listos para proceder a la solución analítica. Pero primero, tomemos una breve digresión sobre qué es la diferenciación y recordemos el significado geométrico de la derivada.

Diferenciación

La diferenciación es la operación de encontrar la derivada de una función.

¿Para qué es un derivado? La derivada de una función caracteriza la tasa de cambio de una función e indica su dirección. Si la derivada en un punto dado es positiva, entonces la función aumenta, de lo contrario, la función disminuye. Y cuanto mayor sea el valor del módulo derivado, mayor será la tasa de cambio de los valores de la función, así como más inclinado el ángulo de la gráfica de la función.

Por ejemplo, bajo las condiciones del sistema de coordenadas cartesianas, el valor de la derivada en el punto M (0,0) igual a +25 significa que en un punto dado, cuando el valor se desplaza $$$x$ derecho a unidad arbitraria, valor $$$y$ aumenta en 25 unidades convencionales. En el gráfico, parece un ángulo de elevación bastante empinado $$$y$ desde un punto dado.

Otro ejemplo. Un valor derivado de -0.1 significa que cuando se compensa $$$x$ por unidad convencional, valor $$$y$ disminuye en solo 0.1 unidades convencionales. Al mismo tiempo, en el gráfico de funciones, podemos observar una inclinación hacia abajo apenas perceptible. Haciendo una analogía con la montaña, parece que estamos descendiendo muy lentamente la suave pendiente de la montaña, a diferencia del ejemplo anterior, donde tuvimos que tomar picos muy empinados :)

Así, después de diferenciar la función $$$ERR (x) = \ sum \ limits_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ por coeficientes $$$a$ y $$$b$ , definimos las ecuaciones de derivadas parciales de primer orden. Después de definir las ecuaciones, obtenemos un sistema de dos ecuaciones, decidiendo cuáles podemos elegir tales valores de los coeficientes $$$a$ y $$$b$ en el cual los valores de las derivadas correspondientes en puntos dados cambian en un valor muy, muy pequeño, y en el caso de la solución analítica no cambian en absoluto. En otras palabras, la función de error en los coeficientes encontrados alcanza un mínimo, ya que los valores de las derivadas parciales en estos puntos serán cero.

Entonces, de acuerdo con las reglas de diferenciación, la ecuación de la derivada parcial del primer orden con respecto al coeficiente $$$a$ tomará la forma:

$$

$$2na + 2b \ sum \ limits_ {i = 1} ^ nx_i - 2 \ sum \ limits_ {i = 1} ^ ny_i = 2 (na + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i)$$

Ecuación derivada parcial de primer orden con respecto a $$$b$ tomará la forma:

$$

$$2a \ sum \ limits_ {i = 1} ^ nx_i + 2b \ sum \ limits_ {i = 1} ^ nx ^ 2_i - 2 \ sum \ limits_ {i = 1} ^ nx_iy_i = 2 \ sum \ limits_ {i = 1} ^ nx_i (a + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i)$$

Como resultado, obtuvimos un sistema de ecuaciones que tiene una solución analítica bastante simple:

\ begin {ecuación *}
\ begin {cases}
na + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i = 0
\\
\ sum \ limits_ {i = 1} ^ nx_i (a + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i) = 0
\ end {casos}
\ end {ecuación *}

Antes de resolver la ecuación, precargue, verifique la carga correcta y formatee los datos.

Descargar y formatear datos

Cabe señalar que debido al hecho de que para la solución analítica, y más tarde para el gradiente y el descenso del gradiente estocástico, usaremos el código en dos variaciones: usando la biblioteca NumPy y sin usarla, necesitaremos formatear los datos en consecuencia (ver código).

Visualización

Ahora, después de que, en primer lugar, descargamos los datos, en segundo lugar, verificamos la carga correcta y finalmente formateamos los datos, realizaremos la primera visualización. A menudo, el método de diagrama de pares de la biblioteca Seaborn se utiliza para esto. En nuestro ejemplo, debido a los números limitados, no tiene sentido usar la biblioteca Seaborn . Utilizaremos la biblioteca Matplotlib normal y solo veremos el diagrama de dispersión.


Anexo No. 1 "Dependencia de ingresos en el mes del año"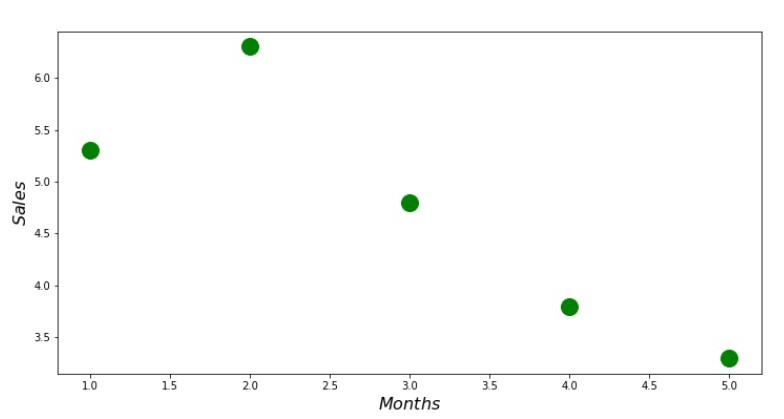

Solución analítica

Utilizaremos las herramientas más comunes en python y resolveremos el sistema de ecuaciones:

\ begin {ecuación *}
\ begin {cases}
na + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i = 0
\\
\ sum \ limits_ {i = 1} ^ nx_i (a + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i) = 0
\ end {casos}
\ end {ecuación *}

De acuerdo con la regla de Cramer, encontramos un determinante común, así como determinantes por $$$a$ y por $$$b$ , después de lo cual, dividiendo el determinante por $$$a$ en el determinante común: encontramos el coeficiente $$$a$ de manera similar, encuentre el coeficiente $$$b$ .


Esto es lo que tenemos:



Entonces, se encuentran los valores de los coeficientes, se establece la suma de las desviaciones al cuadrado. Dibujamos una línea recta en el histograma de dispersión de acuerdo con los coeficientes encontrados.


Anexo No. 2 "Respuestas correctas y estimadas"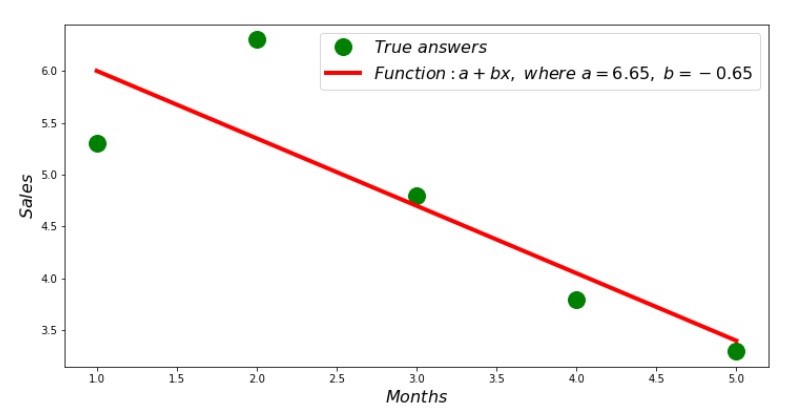



Puede consultar el calendario de desviaciones de cada mes. En nuestro caso, no podemos sacarle ningún valor práctico significativo, pero satisfaceremos la curiosidad de cuán bien la ecuación de regresión lineal simple caracteriza la dependencia de los ingresos en el mes del año.


Anexo No. 3 "Desviaciones,%"



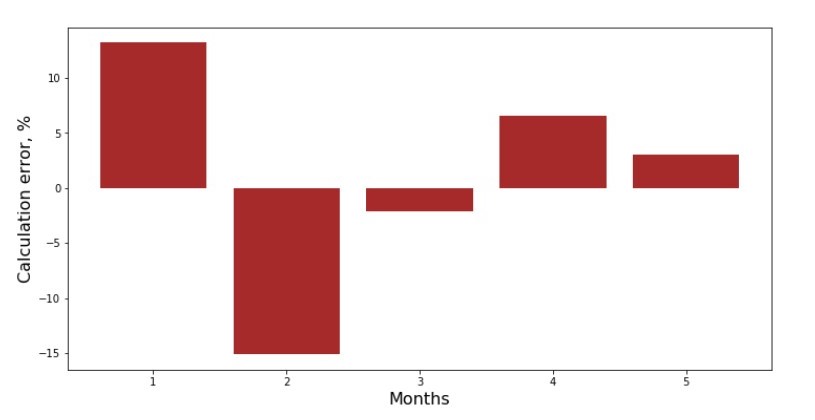
No es perfecto, pero completamos nuestra tarea.

Escribimos una función que, para determinar los coeficientes $$$a$ y $$$b$ usa la biblioteca NumPy , más precisamente, escribiremos dos funciones: una usando una matriz pseudo-inversa (no recomendada en la práctica, ya que el proceso es computacionalmente complejo e inestable), la otra usando una ecuación de matriz.


Compare el tiempo necesario para determinar los coeficientes. $$$a$ y $$$b$ , de acuerdo con los 3 métodos presentados.




En una pequeña cantidad de datos, aparece una función "autoescrita" que encuentra los coeficientes utilizando el método de Cramer.

Ahora puede pasar a otras formas de encontrar los coeficientes $$$a$ y $$$b$ .

Descenso de gradiente

Primero, definamos qué es un gradiente. De manera simple, un gradiente es un segmento que indica la dirección del crecimiento máximo de una función. Por analogía con una subida cuesta arriba, donde se ve el gradiente, hay la subida más empinada hasta la cima de la montaña. Al desarrollar el ejemplo de la montaña, recordamos que, de hecho, necesitamos el descenso más pronunciado para llegar a las tierras bajas lo antes posible, es decir, el mínimo, el lugar donde la función no aumenta ni disminuye. En este punto, la derivada será cero. Por lo tanto, no necesitamos un gradiente, sino un anti-gradiente. Para encontrar el anti-gradiente, solo necesita multiplicar el gradiente por -1 (menos uno).

Llamamos la atención sobre el hecho de que una función puede tener varios mínimos, y habiendo descendido a uno de ellos de acuerdo con el algoritmo propuesto a continuación, no podremos encontrar otro mínimo que sea posiblemente más bajo que el encontrado. ¡Relájate, no estamos en peligro! En nuestro caso, estamos tratando con un mínimo único, ya que nuestra función $$$\ sum \ limits_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ en el gráfico hay una parábola ordinaria. Y como todos deberíamos saber muy bien del curso de matemáticas de la escuela, la parábola solo tiene un mínimo.

Después de descubrir por qué necesitábamos un gradiente, y también que el gradiente es un segmento, es decir, un vector con coordenadas dadas, que son exactamente los mismos coeficientes $$$a$ y $$$b$ podemos implementar gradiente de descenso.

Antes de comenzar, sugiero leer algunas oraciones sobre el algoritmo de descenso:

• Determinamos las coordenadas de los coeficientes de forma pseudoaleatoria $$$a$ y $$$b$ . En nuestro ejemplo, determinaremos los coeficientes cercanos a cero. Esta es una práctica común, pero cada práctica puede tener su propia práctica.
• De coordinar $$$a$ reste el valor de la derivada parcial del primer orden en el punto $$$a$ . Entonces, si la derivada es positiva, entonces la función aumenta. Por lo tanto, quitando el valor de la derivada, nos moveremos en la dirección opuesta del crecimiento, es decir, en la dirección del descenso. Si la derivada es negativa, entonces la función en este punto disminuye y quitando el valor de la derivada nos movemos hacia el descenso.
• Realizamos una operación similar con la coordenada $$$b$ : resta el valor de la derivada parcial en el punto $$$b$ .
• Para no saltar al mínimo y no volar al espacio lejano, es necesario establecer el tamaño del escalón hacia el descenso. En general, puede escribir un artículo completo sobre cómo configurar correctamente el paso y cómo cambiarlo durante el descenso para reducir el costo de los cálculos. Pero ahora tenemos una tarea ligeramente diferente, y estableceremos el tamaño del paso mediante el método científico de "hurgar" o, como dicen en la gente común, empíricamente.
• Después de que somos de las coordenadas dadas $$$a$ y $$$b$ restando los valores de las derivadas, obtenemos nuevas coordenadas $$$a$ y $$$b$ . Tomamos el siguiente paso (resta), ya de las coordenadas calculadas. Y así, el ciclo comienza una y otra vez, hasta que se logra la convergencia requerida.

Eso es todo! Ahora estamos listos para ir en busca del desfiladero más profundo de la Fosa de las Marianas. Bajando




Nos sumergimos hasta el fondo de la Fosa de las Marianas y allí encontramos los mismos valores de los coeficientes. $$$a$ y $$$b$ , que de hecho era de esperar.

Hagamos otra inmersión, solo que esta vez, el llenado de nuestro vehículo de aguas profundas será otras tecnologías, a saber, la biblioteca NumPy .



Valores coeficientes $$$a$ y $$$b$ inmutable

Veamos cómo cambió el error durante el descenso del gradiente, es decir, cómo cambió la suma de las desviaciones al cuadrado con cada paso.


Gráfico №4 "La suma de los cuadrados de las desviaciones en el descenso del gradiente"



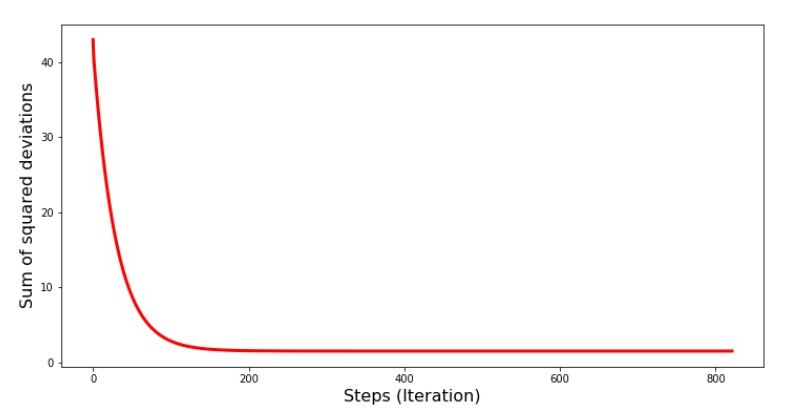
En el gráfico vemos que con cada paso el error disminuye, y después de un cierto número de iteraciones observamos una línea prácticamente horizontal.

Finalmente, estimamos la diferencia en el tiempo de ejecución del código:




Quizás estamos haciendo algo mal, pero una vez más, una función simple "autoescrita" que no usa la biblioteca NumPy está adelantada usando la función que usa la biblioteca NumPy .

Pero no nos quedamos quietos, sino que avanzamos hacia el estudio de otra forma emocionante de resolver la ecuación de la regresión lineal simple. Conoceme

Descenso de gradiente estocástico

Para comprender rápidamente el principio de funcionamiento del descenso de gradiente estocástico, es mejor determinar sus diferencias con respecto al descenso de gradiente ordinario. Nosotros, en el caso de gradiente descendente, en las ecuaciones de derivadas de $$$a$ y $$$a$ usó las sumas de los valores de todos los atributos y las respuestas verdaderas disponibles en la muestra (es decir, las sumas de todos $$$x_i$ y $$$y_i$ ) En el descenso de gradiente estocástico, no utilizaremos todos los valores disponibles en la muestra, sino que, de manera pseudoaleatoria, elegiremos el llamado índice de muestra y utilizaremos sus valores.

Por ejemplo, si el índice está determinado por el número 3 (tres), entonces tomamos los valores $$$x_3 = 3$ y $$$y_3 = $ 4.$ , luego sustituimos los valores en las ecuaciones de derivadas y determinamos las nuevas coordenadas. Luego, una vez determinadas las coordenadas, nuevamente determinamos de forma seudoaleatoria el índice de la muestra, sustituimos los valores correspondientes al índice en las ecuaciones diferenciales parciales y determinamos las coordenadas de una manera nueva. $$$a$ y $$$a$ etc. antes de reverdecer la convergencia. A primera vista, puede parecer que esto puede funcionar, pero funciona. Es cierto que vale la pena señalar que no todos los pasos reducen el error, pero la tendencia ciertamente existe.

¿Cuáles son las ventajas del descenso de gradiente estocástico sobre el habitual? Si nuestro tamaño de muestra es muy grande y se mide en decenas de miles de valores, entonces es mucho más fácil de procesar, digamos miles de ellos al azar que la muestra completa. En este caso, se inicia el descenso de gradiente estocástico. En nuestro caso, por supuesto, no notaremos una gran diferencia.

Nos fijamos en el código.




Observamos cuidadosamente los coeficientes y nos damos cuenta de la pregunta "¿Cómo es eso?". Tenemos otros valores de los coeficientes. $$$a$ y $$$b$ . ¿Quizás el descenso de gradiente estocástico encontró parámetros más óptimos de la ecuación? Por desgracia no. Es suficiente mirar la suma de las desviaciones al cuadrado y ver que con los nuevos valores de los coeficientes, el error es mayor. No te apresures a la desesperación. Trazamos el cambio de error.


Gráfico №5 “La suma de los cuadrados de las desviaciones en el descenso de gradiente estocástico”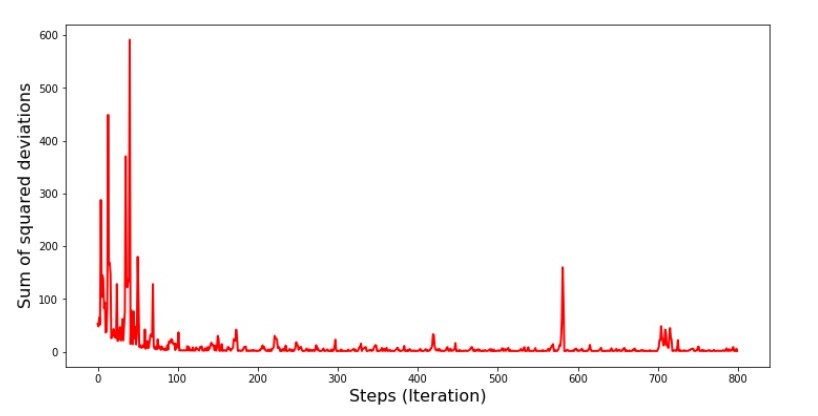



Después de mirar el cronograma, todo encaja y ahora lo arreglaremos todo.

Entonces que paso? Lo siguiente sucedió.Cuando seleccionamos aleatoriamente un mes, es para el mes seleccionado que nuestro algoritmo busca reducir el error al calcular los ingresos. Luego seleccionamos otro mes y repetimos el cálculo, pero ya reducimos el error para el segundo mes seleccionado. Y ahora recordemos que durante los primeros dos meses nos hemos desviado significativamente de la línea de la ecuación de regresión lineal simple. Esto significa que cuando se selecciona cualquiera de estos dos meses, y luego se reduce el error de cada uno de ellos, nuestro algoritmo aumenta seriamente el error en toda la muestra. Entonces que hacer? La respuesta es simple: necesita reducir el paso de descenso. Después de todo, al disminuir el paso de descenso, el error también dejará de "saltar" hacia arriba y hacia abajo. Por el contrario, el error "omitir" no se detendrá, pero no lo hará tan rápido :) Lo comprobaremos.




Gráfico No. 6 "La suma de los cuadrados de las desviaciones en el descenso de gradiente estocástico (80 mil pasos)"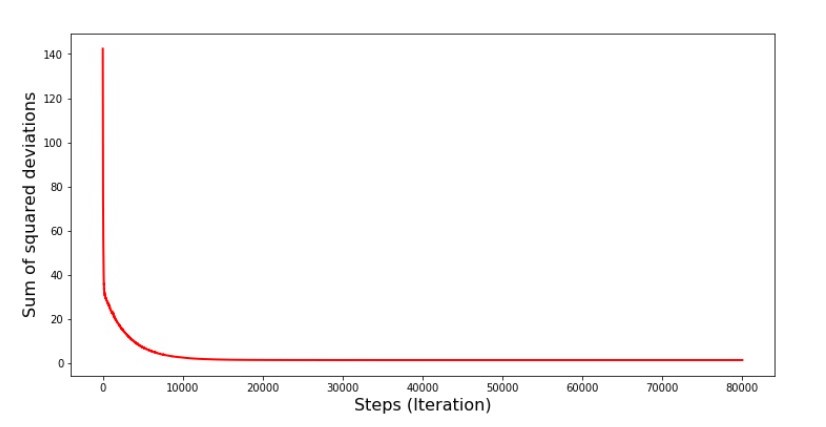



Los valores de los coeficientes mejoraron, pero aún no son ideales. Hipotéticamente, esto se puede corregir de esta manera. Por ejemplo, en las últimas 1000 iteraciones, elegimos los valores de los coeficientes con los que se cometió el error mínimo. Es cierto que para esto tendremos que anotar los valores de los coeficientes. No haremos esto, sino que prestaremos atención al horario. Se ve suave y el error parece disminuir de manera uniforme. Este no es realmente el caso. Veamos las primeras 1000 iteraciones y compárelas con la última.


Programa No. 7 “La suma de los cuadrados de las desviaciones del SGD (primeros 1000 pasos)”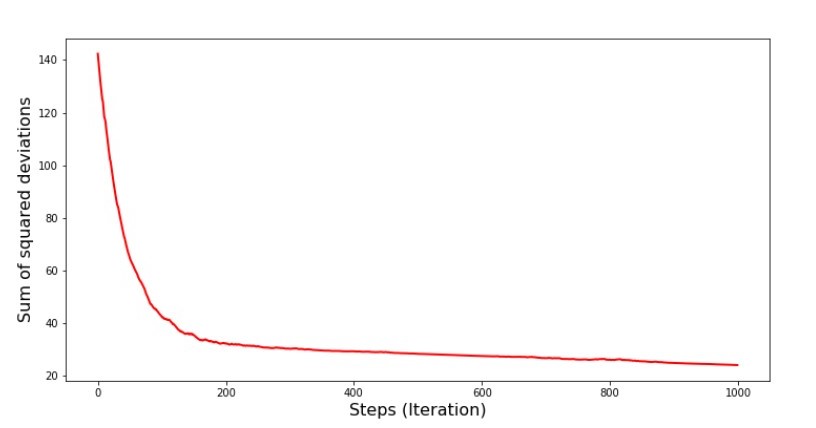



Gráfico No. 8 “La suma de los cuadrados de las desviaciones del SGD (últimos 1000 pasos)”



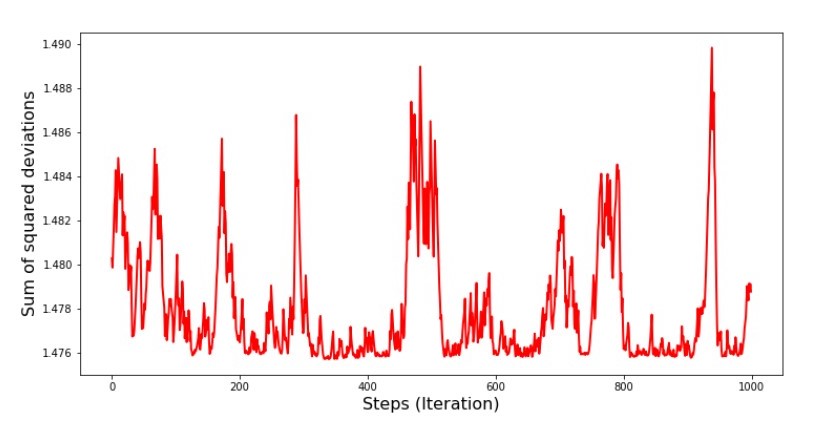Al comienzo del descenso, observamos una disminución de error bastante uniforme y aguda. En las últimas iteraciones, vemos que el error da vueltas y vueltas alrededor de un valor de 1.475 y en algunos puntos incluso es igual a este valor óptimo, pero luego sube de todos modos ... Nuevamente, puedo anotar los valores de los coeficientes$$$a$ y $$b , y luego seleccione aquellos para los cuales el error es mínimo. Sin embargo, tuvimos un problema más serio: tuvimos que dar 80 mil pasos (ver código) para obtener valores cercanos a lo óptimo. Y esto ya contradice la idea de ahorrar tiempo computacional con un descenso de gradiente estocástico en relación con el gradiente. ¿Qué se puede corregir y mejorar? No es difícil notar que en las primeras iteraciones bajamos con confianza y, por lo tanto, debemos dejar un gran paso en las primeras iteraciones y reducir el paso a medida que avanzamos. No haremos esto en este artículo, ya se ha prolongado. Aquellos que lo deseen pueden pensar cómo hacer esto, no es difícil :)Ahora realizaremos un descenso de gradiente estocástico usando la bibliotecaNumPy$b$

(y no tropezaremos con las piedras que identificamos anteriormente)




Los valores resultaron ser casi los mismos que durante el descenso sin usar NumPy . Sin embargo, esto es lógico.

Descubriremos cuánto tiempo nos llevaron los descensos de gradiente estocástico.




Cuanto más se adentra en el bosque, más oscuras son las nubes: nuevamente, la fórmula "autoescrita" muestra el mejor resultado. Todo esto sugiere que debería haber formas aún más sutiles de usar la biblioteca NumPy , lo que realmente acelera las operaciones de los cálculos. En este artículo no nos enteramos de ellos. Habrá algo en qué pensar cuando lo desee :)

Resumir

Antes de resumir, me gustaría responder la pregunta que probablemente surgió de nuestro querido lector. ¿Por qué, de hecho, tal "tormento" con descensos, por qué tenemos que subir y bajar la montaña (principalmente hacia abajo) para encontrar la preciada tierra baja, si tenemos un dispositivo tan poderoso y simple en nuestras manos, en forma de una solución analítica que nos teletransporta instantáneamente a lugar correcto?

La respuesta a esta pregunta se encuentra en la superficie. Ahora hemos examinado un ejemplo muy simple en el que la respuesta verdadera$$y yo depende de un atributo$y_i$$$$x_i$ .En la vida, esto no se ve a menudo, así que imagina que tenemos signos de 2, 30, 50 o más. Agregue a esto miles, o incluso decenas de miles de valores para cada atributo. En este caso, la solución analítica puede no pasar la prueba y fallar. A su vez, el descenso del gradiente y sus variaciones nos acercarán lenta pero seguramente a la meta: el mínimo de la función. Y no se preocupe por la velocidad: probablemente también analicemos métodos que nos permitirán establecer y ajustar la longitud del paso (es decir, la velocidad).

Y ahora en realidad un breve resumen.

En primer lugar, espero que el material presentado en el artículo ayude a los principiantes a "salir con científicos" a comprender cómo resolver las ecuaciones de regresión lineal simple (y no solo).

En segundo lugar, examinamos varias formas de resolver la ecuación. Ahora, dependiendo de la situación, podemos elegir el que mejor se adapte para resolver el problema.

En tercer lugar, vimos el poder de las configuraciones adicionales, a saber, la longitud del paso del descenso del gradiente. Este parámetro no puede ser descuidado. Como se señaló anteriormente, para reducir el costo de los cálculos, la longitud del paso debe cambiarse a lo largo del descenso.

Cuarto, en nuestro caso, las funciones "autoescritas" mostraron el mejor resultado temporal de los cálculos. Esto probablemente se deba al uso no profesional de las capacidades de la biblioteca NumPy. Pero sea como sea, la conclusión es la siguiente. Por un lado, a veces vale la pena cuestionar las opiniones establecidas, y por otro, no siempre vale la pena complicar las cosas; por el contrario, a veces una forma más simple de resolver un problema es más efectiva. Y dado que nuestro objetivo era analizar tres enfoques para resolver la ecuación de la regresión lineal simple, el uso de funciones "autoescritas" fue suficiente para nosotros.

← Trabajo previo del autor - “Estudiamos la declaración del teorema del límite central usando la distribución exponencial”$\leftarrow$
→ El próximo trabajo del autor - "Traemos la ecuación de regresión lineal en forma de matriz"$\rightarrow$

Literatura (o algo así)

1. Regresión lineal

http://statistica.ru/theory/osnovy-lineynoy-regressii/

2. Método de mínimos cuadrados

mathprofi.ru/metod_naimenshih_kvadratov.html

3. Derivado

www.mathprofi.ru/chastnye_proizvodnye_primery.html

4. Gradiente

matemático /proizvodnaja_po_napravleniju_i_gradient.html

5. Descenso de gradiente

habr.com/en/post/471458

habr.com/en/post/307312

artemarakcheev.com//2017-12-31/linear_regression

6. NumPy library

docs.scipy.org/doc/ numpy-1.10.1 / reference / generate / numpy.linalg.solve.html

docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.pinv.html

pythonworld.ru/numpy/2. html