Examinamos el método de Monte Carlo , hoy veremos cómo juega la mente de la computadora en 2048 usando el viejo minimax con recorte alfa-beta.

Este artículo fue escrito con el apoyo de EDISON, una compañía que desarrolla aplicaciones móviles y brinda servicios de prueba de software .
Solución espiada por el usuario stackoverflow
 ovolve
ovolve , quien señaló en la discusión
cómo enseñar a AI el juego 2048 .
Traducción de comentarios de ovolveSoy el autor del programa mencionado en este hilo. Puedes ver la IA
en acción o ver
el código .
Actualmente, el programa gana en aproximadamente el 90% de los casos al ejecutar java-scripts en un navegador en mi computadora portátil, gastando 100 milisegundos para pensar en el curso, trabajando, aunque no perfectamente, pero bastante bien.
Dado que el juego es un espacio de estado discreto con información completa, de hecho es un juego por turnos como el ajedrez y las damas, utilicé los mismos métodos que mostraron su rendimiento en estos juegos, es decir,
búsqueda de minimax con
recorte alfa-beta . Como los enlaces proporcionan mucha información sobre este algoritmo, solo hablaré sobre las dos heurísticas principales que utilicé en
la función de estimación estática y formalizaré muchas de las suposiciones intuitivas hechas por otras personas aquí.

Monotonía
Esta heurística trata de garantizar que todos los valores de mosaico aumenten o disminuyan tanto hacia la izquierda / derecha como hacia arriba / abajo. Esta heurística por sí sola refleja la conjetura de que muchos otros han mencionado que los mosaicos más valiosos deberían agruparse en una esquina. Esto, por regla general, evita la acumulación de fichas menos valiosas y mantiene el tablero organizado, ya que las fichas más pequeñas caen en cascada en las más grandes.
Aquí hay una captura de pantalla de una cuadrícula completamente monótona. Obtuve esta situación ejecutando un algoritmo con la función eval instalada para ignorar otras heurísticas y tener en cuenta solo la monotonía.

Suavidad (suavidad, uniformidad)
La heurística anterior en sí misma tiende a crear estructuras en las cuales las celdas vecinas tienen un valor reducido, sin embargo, por supuesto, las vecinas deben tener el mismo significado para combinar. Por lo tanto, la heurística de suavidad simplemente mide la diferencia de valores entre las fichas adyacentes, tratando de minimizar su número.
Un comentarista de Hacker News proporcionó una
interesante formalización de esta idea en términos de teoría de grafos.
Traducción de formalización con Hacker NewsAyer le mostré este juego a un colega, un amante de la teoría de gráficos, y también decidimos pensar en cómo resolver este juego usando IA.
La solución más simple es minimax, que, según lo veo, se implementa bastante bien. Si alguien aquí no está familiarizado con minimax, OP escribió un código muy elegante y bien comentado que sería un gran tutorial.
El enfoque menos computacionalmente intensivo que propusimos fue modelar el estado del juego en forma de un gráfico G (V, E) , donde V es un conjunto de fichas activas y E es un conjunto de bordes que conectan fichas adyacentes ponderadas por la función c (v1, v2) , que devuelve el valor absoluto de la diferencia entre los dos mosaicos. Para cada solución, la IA elige un movimiento que minimiza la suma de los pesos de todos los bordes en el nuevo estado del juego.
La razón de esto es que la única forma de progresar en el juego es tener fichas con los mismos valores uno al lado del otro, para lo cual el peso en G será 0. Por lo tanto, la IA debería tratar de minimizar el peso total. Al final, habrá un gran número en los tableros con un gran peso de bordes a las fichas adyacentes, por lo que la IA intentará mantener estas fichas junto a otras fichas grandes para minimizar la diferencia.
Como el juego es estocástico, el enfoque que describí puede no funcionar en el peor de los casos, pero también se puede aplicar a la solución minimax existente como una función de peso para cada nodo en el árbol.
Aquí hay una captura de pantalla de una malla perfectamente lisa, amablemente proporcionada por este excelente
tenedor simulado .
(enlace al archivo web, mientras que los scripts de Java en la página funcionan y puede usar el teclado para moverse en cualquier dirección - nota del traductor).Azulejos sueltos
Y finalmente, hay una penalización por tener muy pocas fichas libres, ya que las opciones pueden terminar rápidamente cuando el campo de juego se vuelve demasiado estrecho.
¡Y eso es todo! Buscar en el espacio del juego mientras se optimizan estos criterios ofrece un rendimiento sorprendentemente bueno. Uno de los beneficios de utilizar un enfoque genérico como este en lugar de una estrategia de movimiento codificada explícitamente es que el algoritmo a menudo puede encontrar soluciones interesantes e inesperadas. Si observa su progreso, a menudo realiza movimientos sorprendentes pero efectivos, como el cambio repentino de muros o esquinas, cerca de los cuales construye su juego.

Pequeño cambio
La captura de pantalla demuestra el poder de este enfoque. Eliminé el límite de mosaico (para que continúen creciendo después de llegar a 2048), y aquí está el mejor resultado después de ocho pruebas.
Sí, esto es 4096 junto con 2048. =) Esto significa que ha alcanzado la esquiva ficha 2048 en un tablero.
El código Java-Script para minimax con recorte alfa-beta y función de evaluación estática del usuario ovolve stackoverflow se detalla a continuación en el artículo.
El método minimax está dedicado a varios excelentes artículos habr, por lo que omitimos la explicación académica detallada de en qué consiste. Para aquellos que se
unieron a la comunidad de TI, recientemente escuché los hermosos términos "minimax" y "recorte alfa-beta", pero no sé lo que esto significa, intentemos, literalmente en un par de párrafos, explicar el significado más general.
Minimax
En algunos juegos, el proceso de un juego entre dos jugadores (que hacen un movimiento a su vez) puede representarse como un llamado árbol de opciones. En cada posición específica, cada jugador generalmente puede elegir entre diferentes opciones para su movimiento. Y en respuesta a cada una de estas opciones, un oponente también puede ser de muchas maneras.
Fragmento de un árbol de opciones.Dado que en cualquier momento del juego hay información completa sobre el estado del campo de juego, el estado actual de la posición siempre se puede estimar con precisión. Dicha función se denomina
función de evaluación estática o
SFO abreviada. Además, cuanto más importante es esta función al evaluar una posición específica, más ventajosa es la posición para un jugador (llamémosle
jugador maximizador ). Cuanto más pequeño es el valor numérico de esta función al evaluar una posición, más ventajosa es la posición para el segundo jugador (llamémoslo el
jugador que minimiza ).
Después de cada movimiento, la posición cambia y, por lo tanto, su puntaje cambia. Al considerar el árbol de opciones, cada jugador necesita no solo preferir aquellas ramas en las que la calificación es más favorable para él. También debes evitar aquellas ramas en las que la evaluación de la posición es favorable para el oponente.
Se supone que el oponente también se guía por el racionalismo y también evita opciones que podrían llevarlo a perder. Es decir, cada jugador, al elegir una opción, procede a maximizar su propio beneficio y al mismo tiempo minimizar el beneficio del oponente.
Esto es minimax.
Recorte alfa beta
Es bastante obvio: quien calcula un árbol desde una posición dada a una mayor profundidad, tiene más posibilidades de ganar. Pero hay una molestia: el árbol de opciones en los juegos tiene el desagradable hábito de ramificarse y crecer exponencialmente con cada nivel de anidación. Las habilidades de conteo de los programas, y aún más por lo que las personas son limitadas, el conteo "hasta el tapete" está lejos de ser siempre posible. Puede resultar fácilmente que un jugador ha contado hasta una posición en la que tiene una buena evaluación del campo de juego, pero literalmente en el siguiente nivel (ilegible) el oponente tiene la oportunidad de hacer un movimiento que cambie radicalmente la estimación de la posición al contrario.
¿Quién tiene la culpa y qué hacer? La complejidad computacional es la responsable del recorrido completo del árbol; se propone luchar cortando ramas innecesarias. Si el jugador que evalúa la posición ve que alguna rama del árbol de opciones:
o menos rentable para él que otras ramas que ya han sido analizadas,
o más beneficioso para el oponente que otras ramas que ya han sido analizadas,
entonces el jugador descarta esta rama, no pierde tiempo y recursos al considerar las subopciones de esta rama obviamente peor para él.
Esto le permite asignar más recursos informáticos para calcular ramas más favorables a una mayor profundidad de representación en el árbol de opciones. En el proceso de evaluar el campo de juego en diferentes niveles del árbol de opciones, el jugador opera con dos coeficientes que cambian dinámicamente:
alfa (el valor del SFD que se encuentra mínimamente en la rama, es decir, más favorable para el jugador que minimiza) y
beta (el valor del SFD que se encuentra más en la rama, es decir, más favorable para el jugador maximizador). En cada nivel, comparar el SFD de la posición actual con
los coeficientes
alfa y
beta le permite barrer (sin calcularlos completamente) ramas que son
menos beneficiosas para el jugador que evalúa la posición y / o
más beneficioso para su oponente.
Este es el recorte alfa beta.
Función minimax recursiva con recorte alfa beta
2048 con AI se implementa como una aplicación de Excel con macros VBA, así es como el algoritmo minimax con recorte alfa beta parece un básico visual despreciable. Código Ovolve en java-script function AI(grid) { this.grid = grid; }
Función de evaluación estática
Dado que en cada nivel del árbol de opciones tienes que evaluar el campo de juego (para decidir cuál de los jugadores, la posición estimada es realmente más ventajosa), debes decidir con qué criterios distinguir una buena posición de una mala.
Suponemos que el jugador maximizador es la persona (o IA) que decide en cuál de las 4 direcciones (arriba, izquierda, derecha, abajo) mover todas las fichas. Un jugador que minimiza es esa subrutina insidiosa que genera aleatoriamente 2 o 4 en los lugares más inapropiados.
La OFS se compila desde la perspectiva de un jugador maximizador. Cuanto mayor sea la calificación SFD para el campo de juego, mejor será la posición para el "maximalista". Cuanto más bajo, más agradable es la posición en el tablero para el "minimalista".
En el caso de 2048, ¿qué factores se consideran favorables para quien mueve las fichas?
Monotonía
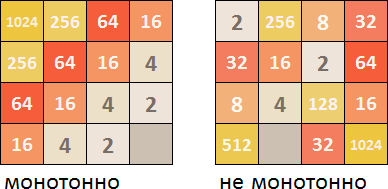
En primer lugar, es deseable que las fichas estén dispuestas en orden ascendente / descendente en algunas direcciones. Si esto no se hace, cuando se generen nuevas fichas, el campo de juego se obstruirá rápidamente con fichas ordenadas al azar de diferentes tamaños, que no pueden conectarse inmediatamente entre sí normalmente.
En el Distrito Federal de Siberia, debe mirar en las 4 direcciones (de arriba hacia abajo, de izquierda a derecha, de derecha a izquierda, de abajo hacia arriba) y calcular dónde están los progresos decrecientes o decrecientes. Si en progresión hay fichas que no encajan en la serie general, esto reduce el coeficiente numérico de la monotonía. Luego, de los 4 coeficientes para todas las direcciones, se selecciona el mejor, que se tiene en cuenta en el valor total del Distrito Federal de Siberia.
Suavidad

Además, sería más preferible que la progresión de estar parado en una fila de fichas no solo aumentara, sino que no disminuyera (o en lugar de disminuirla, es preferible que no aumentara), es decir, es bueno cuando las mismas fichas están cerca, lo que les permite colapsar en una, ganando puntos y aumentando el espacio libre en el campo de juego.
Por lo tanto, el Distrito Federal de Siberia está buscando en el campo de juego fichas adyacentes idénticas y tiene en cuenta el número de tales pares en un coeficiente especial.
Celdas vacías

Obviamente, cuanto más espacio libre, más espacio para maniobrar y menos posibilidades de perder rápidamente.
La OFS considera celdas vacías en el campo y, cuanto más, la posición se considera más rentable para el jugador maximizador.
Azulejo máximo
Dado que lo principal en este juego es obtener un gran mosaico en el campo, cuanto más mejor, 2048, 4096, 8192 (o lo que sea que tenga la fuerza y la paciencia para), las opciones en las que el valor máximo del mosaico es más deben considerarse como el SFD más rentable.
Distrito Federal de Siberia para 2048
Implementación del Distrito Federal de Siberia como macro VBA Código Ovolve en java-script function Grid(size) { this.size = size; this.startTiles = 2; this.cells = []; this.build(); this.playerTurn = true; }
2048.xlsm
La propia aplicación Excel se
puede descargar de Google .
La funcionalidad de la aplicación se describe
en un artículo anterior, donde AI juega usando el método Monte Carlo . La solución de hoy se ha agregado al Monte Carlo existente.
Todos los artículos de la serie AI y 2048.
- Montecarlo
- Recorte de minimax + alfa beta
- Esperando el máximo
- Red neuronal