Algoritmo de búsqueda difusa de TextRadar: enfoques básicos
A diferencia de las comparaciones de cadenas difusas, cuando ambas cadenas comparadas son equivalentes, la cadena de búsqueda y la cadena de datos se resaltan en la tarea de búsqueda difusa, y es necesario determinar no el grado de similitud de las dos cadenas, sino el grado de presencia de la cadena de búsqueda en la cadena de datos.
Declaración del problema.
Una cadena de datos y una cadena de búsqueda se proporcionan como conjuntos de caracteres arbitrarios que consisten en palabras: grupos de caracteres separados por espacios.
Se requiere encontrar en la línea de datos el conjunto de fragmentos más cercano a la línea de búsqueda por la composición y la posición relativa de los caracteres.
Para evaluar la calidad del resultado de la búsqueda, calcule el coeficiente de relevancia, cuyo valor debe estar en el rango de 0 a 1, donde 0 debe corresponder a la ausencia completa de caracteres de la cadena de búsqueda en la cadena de datos, y 1 debe corresponder a la presencia de la cadena de búsqueda en la cadena de datos en la forma no distorsionada.
La búsqueda debe llevarse a cabo mediante un análisis carácter por carácter de las líneas de origen, teniendo en cuenta la disposición mutua de caracteres y palabras en las líneas, pero sin tener en cuenta la sintaxis y la morfología del lenguaje.
Descripción del algoritmo
La búsqueda se lleva a cabo en varias etapas.
Construcción de una matriz de coincidencias.
La matriz de coincidencia (M) es una matriz bidimensional, cuyo número de columnas corresponde a la longitud de la cadena de datos y el número de filas a la longitud de la cadena de búsqueda. Los elementos de la matriz de coincidencia toman los valores 0 o 1 dependiendo de si los caracteres correspondientes de las líneas coinciden o no, con la excepción de espacios (delimitadores de palabras).
La matriz de coincidencia para la cadena de datos "ABCD EF" y la cadena de búsqueda "ABC" tiene la forma:
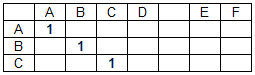
Elemento de matriz de coincidencia m (i, j) = 1 si d (i) = s (j), donde D es una matriz de caracteres de cadena de datos, S es una matriz de caracteres de cadena de búsqueda, i es un número de columna de la matriz de coincidencia M (número de caracteres de una cadena de datos ), j es el número de fila de la matriz de coincidencia (el número del carácter en la cadena de búsqueda). En otros casos, m (i, j) = 0. Las coincidencias de separadores de palabras (en nuestro caso, espacios) no se tienen en cuenta, es decir: m (i, j) = 0 si d (i) = s (j) = '' .
Emparejar diagonales de matriz
Los elementos de la matriz de coincidencia M forman diagonales. Los elementos de la matriz están en la misma diagonal si sus índices i y j difieren simultáneamente en +1 o en - 1.

Las diagonales corresponden a las posiciones de la cadena de búsqueda en la secuencia de desplazamientos a lo largo de la cadena de datos.

Los elementos de una de las diagonales y el desplazamiento correspondiente en la figura anterior se resaltan en azul.
La idea de utilizar una secuencia de cambios de línea entre sí en un problema de búsqueda difusa se remonta a la técnica bien conocida para detectar señales de radar en un contexto de interferencia, que implica el cálculo de la función de correlación mutua de las señales de radio. La función de correlación cruzada determina el grado de similitud de las copias de dos señales diferentes v (t) yu (t), desplazadas por el tiempo τ entre sí y se define como la integral: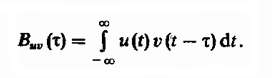
El número total de diagonales se calcula mediante la fórmula:

Las longitudes de las diagonales son iguales a la longitud de la cadena de búsqueda.
Grupos de partidos
Las unidades que siguen en sucesión en las diagonales de la matriz de coincidencia forman grupos de coincidencias. A continuación se muestran los grupos de coincidencia para la cadena de datos "ABCD DEF JH" y la cadena de búsqueda "ABC DE J" - 4 grupos ubicados en diferentes diagonales.

Matrices de proyección
Las diagonales de la matriz de coincidencia y los grupos de coincidencia contenidos en ellas se asignan a las secciones correspondientes de la cadena de búsqueda y la cadena de datos, formando dos matrices de proyección: la cadena de búsqueda y la cadena de datos, respectivamente. Para nuestro ejemplo, las matrices de proyección se verán así:
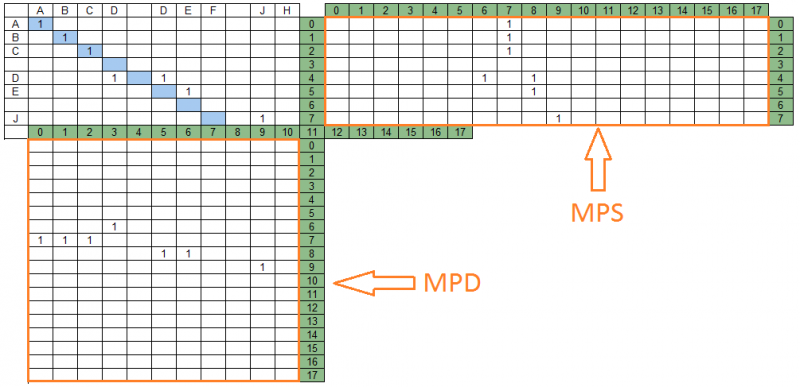
En la figura anterior, a la derecha de la matriz de coincidencia se encuentra la matriz de proyecciones en la cadena de búsqueda - MPS, debajo - la matriz de proyecciones en la cadena de datos MPD. El número de columnas MPS es igual al número de filas MPD e igual al número de diagonales de la matriz de coincidencia; en nuestro ejemplo, hay 18.
Buscar un conjunto de grupos de resultados
Para resolver el problema, es necesario encontrar un conjunto de grupos que "cubra" más la cadena de búsqueda, con la menor fragmentación (lo más grande posible), sin intersecciones mutuas en las matrices de proyección, y la asignación de los cuales en la cadena de datos será más cercana a la cadena de búsqueda "original" .
Intersección de grupos en la matriz de proyección.En nuestro ejemplo, hay grupos que se cruzan en la matriz MPS; en la figura siguiente se resaltan en rojo. Además, en la matriz MPD, estos mismos grupos no se cruzan, en la figura se resaltan en verde.
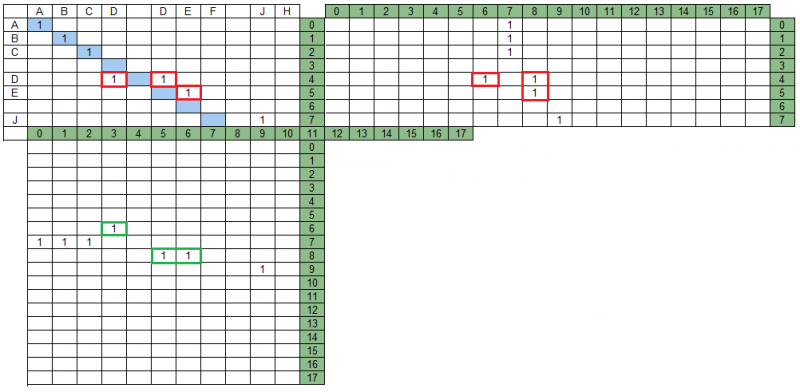
La búsqueda del conjunto de grupos resultante implica que no todos los grupos se incluirán en él y que algunos de los grupos restantes se pueden modificar (truncar) al analizar intersecciones mutuas de grupos en proyecciones.
La búsqueda del conjunto de resultados se puede llevar a cabo pasando por el ciclo "infinito" (el número de iteraciones del ciclo no excede el número de grupos) de la
tabla de todos los grupos , en los que se colocan inicialmente los grupos de la matriz coincidente, en cada iteración se realizarán las siguientes acciones:
- Elegir el mejor de acuerdo con ciertos parámetros (según el contexto del problema que se resuelva); en el caso más simple, esta puede ser la elección del primer grupo del tamaño más grande que se encuentre;
- Colocación del mejor grupo en la tabla de grupos de resultados y su eliminación de la tabla de todos los grupos (cuyas filas se rastrean);
- Eliminar (o truncar) de la tabla de grupos que se cruzan con el mejor grupo seleccionado en las matrices de proyección de grupos.
El conjunto óptimo de grupos para nuestro ejemplo se presenta en la figura siguiente: los grupos de conjuntos se resaltan en naranja.

El grupo eliminado durante el procesamiento de intersección (intersección en la matriz MPS con el mejor grupo de la segunda iteración) se resalta en rojo.
El resultado de la búsqueda en la fila de datos se verá así:

Cálculo del coeficiente de relevancia.
Para una evaluación cuantitativa de los resultados de búsqueda, las longitudes de los grupos encontrados se comparan con las longitudes de palabras de la cadena de búsqueda (evaluación de composición de grupo), así como la longitud total de la cadena de búsqueda con la longitud de los grupos encontrados en la cadena de datos. Se supone que la importancia de evaluar la composición de los grupos encontrados es mayor que la importancia de la estimación de la extensión en la fila de datos, que se tiene en cuenta en los coeficientes de ponderación de la fórmula para calcular el coeficiente de relevancia:

Donde el coeficiente de composición del grupo se calcula como la relación entre la suma de las longitudes al cuadrado de los grupos encontrados y la suma de las longitudes al cuadrado de las palabras de la cadena de búsqueda:

El factor de longitud es la relación entre la longitud de la cadena de búsqueda y la longitud total de los grupos encontrados en la cadena de datos. Si el valor obtenido de esta manera es mayor que 1, se toma su valor inverso:

Para nuestro ejemplo:

Alcance estimado de la computación
Las operaciones más intensivas en recursos son:
- determinación de la matriz de coincidencia M: el número de elementos de la matriz se define como el producto de la longitud de la cadena de búsqueda por la longitud de la cadena de datos: L * L;
- definición de matrices de proyección en datos y cadenas de búsqueda: el número de elementos de la matriz será para MPS: (L + L - 1) * L, para MPD: (L + L - 1) * ;
- la formación de la tabla de todos los grupos: el número de grupos no excederá el valor L * L / 2;
- busque el conjunto de grupos resultante: el número de iteraciones del ciclo no excede el número inicial de grupos, es decir, L * L / 2.
Por lo tanto, la cantidad total de cálculos será un múltiplo del producto de la longitud de la cadena de búsqueda por la longitud de la cadena de datos:

La linealidad de la cantidad de cálculo en relación con el tamaño de los datos de origen es un argumento importante a favor de la aplicación práctica del algoritmo.
No linealidad
Vale la pena señalar que la linealidad se debe a un procedimiento simplificado para encontrar el conjunto resultante de grupos. En el caso general, si consideramos todas las opciones posibles para colocar grupos en una fila de datos teniendo en cuenta las posibles opciones de procesamiento de intersección y seleccionamos el mejor
conjunto de grupos del conjunto de posibles, en lugar de elegir
un grupo en cada iteración del ciclo, la cantidad de cálculos dejará de ser lineal con respecto al tamaño fuente de datos. La dependencia no lineal de la cantidad de cómputo del tamaño de los datos fuente limita enormemente las posibilidades de aplicación práctica.
Encuentra el equilibrio
Para garantizar el equilibrio óptimo entre la calidad de la búsqueda y la necesidad de recursos, es importante elegir la metodología de búsqueda correcta para el conjunto resultante de grupos, que, por regla general, se puede hacer utilizando las características de contexto del problema que se está resolviendo.
Se ha implementado un soporte de demostración en el
sitio web
textradar.ru donde puede probar el funcionamiento del algoritmo.
Comparación con análogos:
Comparación del algoritmo de búsqueda difusa TextRadar con análogos: Lucene, Sphinx, Yandex, 1C