Una de las tareas más difíciles en los sistemas de diseño asistidos por computadora es el fileteado al modelar objetos de formas complejas. Para la construcción de filetes, así como para toda la geometría en CAD, el núcleo geométrico es responsable.

Desde el punto de vista del desarrollador del núcleo, es imposible cubrir todas las opciones de redondeo debido a su variedad infinita. Nuestros matemáticos constantemente agregan nuevos casos especiales al núcleo C3D, y recientemente han realizado un redondeo de tres caras (o redondeo completo).

¿Cuál es su complejidad y cómo funciona el algoritmo ?, dice Anna Ladilova, matemática y programadora de C3D Labs.

¿Qué es el redondeo completo?

Supongamos que tenemos un cuerpo con tres cadenas de caras: central (superior) y lateral (derecha e izquierda). Se requiere reemplazar la cara central con una superficie de filete que encajaría suavemente en las caras laterales adyacentes. Esta nueva superficie estará completamente redondeada. En general, tiene un radio variable que se detecta automáticamente.



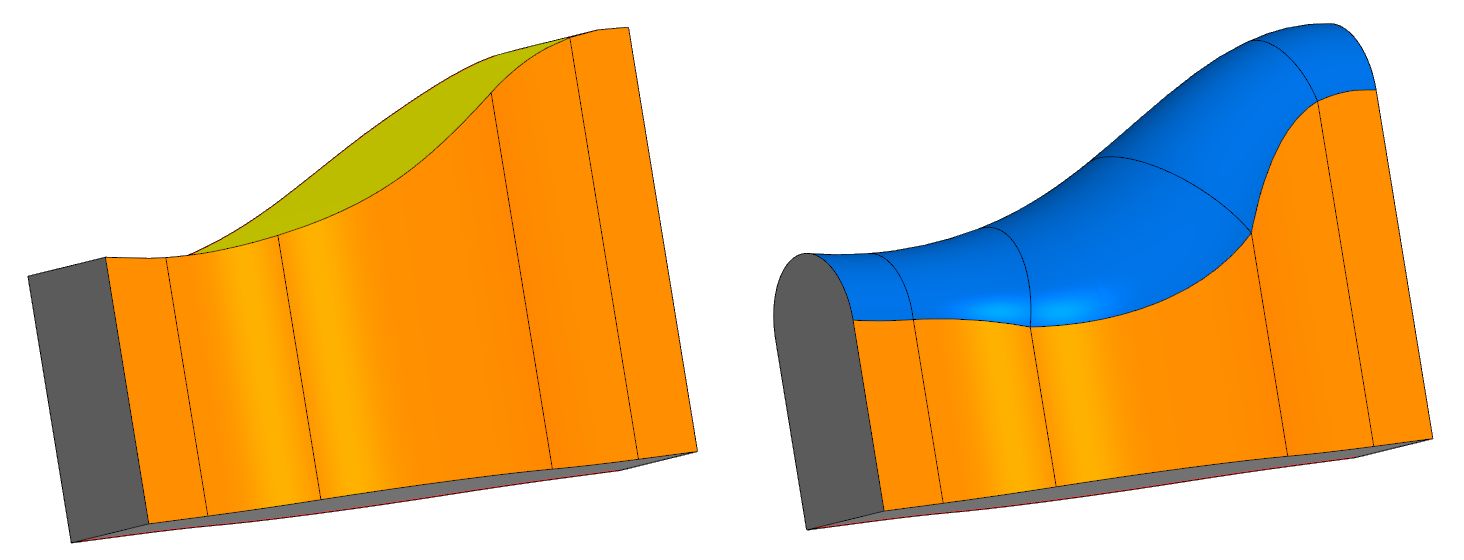
En muchos sistemas CAD conocidos, se implementa la operación de redondeo completo, pero no se revelan sus matemáticas.


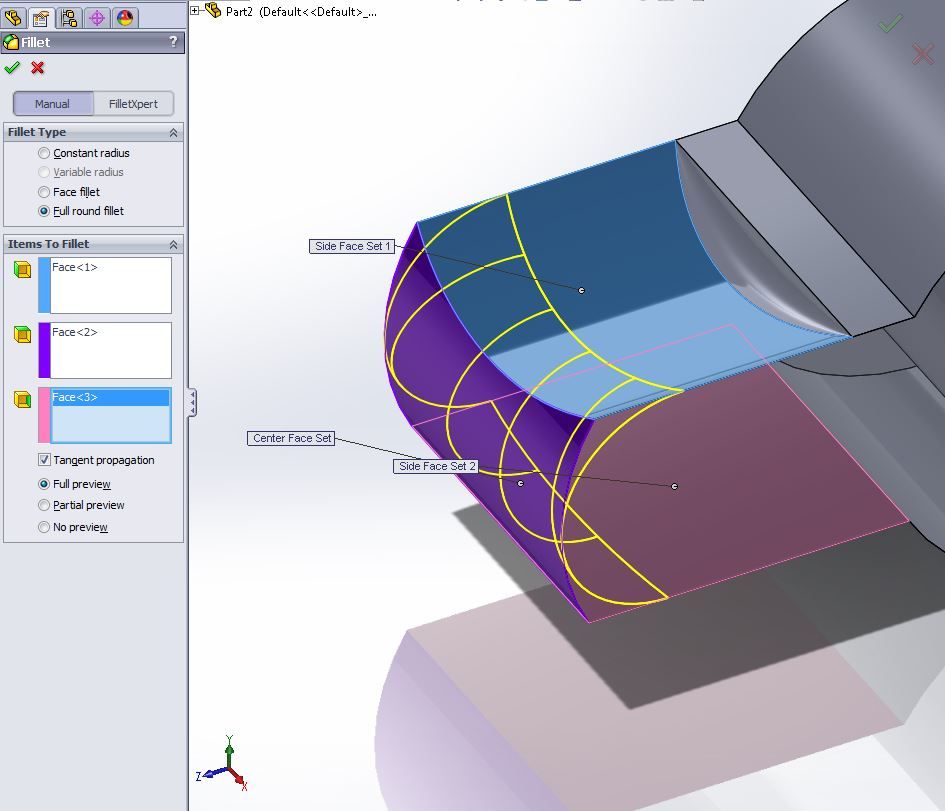Operación de filete redondo completo de Solidworks

Por lo tanto, desarrollamos nuestro propio algoritmo. Y difiere de los algoritmos de otros desarrolladores.

Las operaciones, aunque se llaman igual, conducen a resultados ligeramente diferentes. Esto sugiere que SolidWorks ofrece una definición diferente para redondear tres caras.


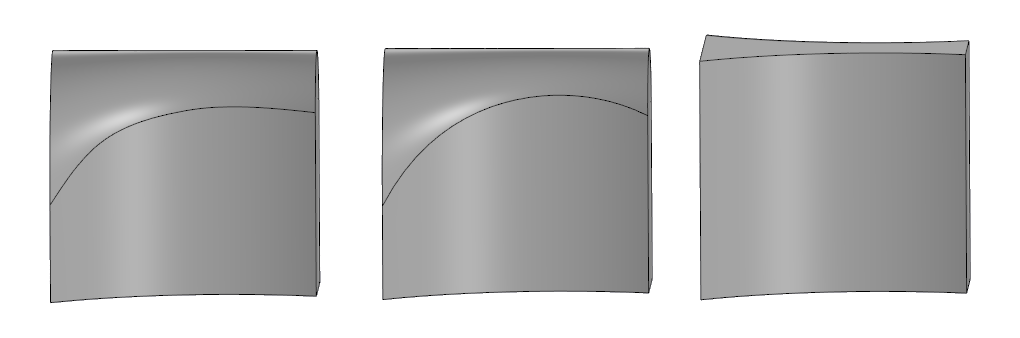A la derecha está el modelo original, en el centro hay un redondeo completo en SolidWorks, a la izquierda, en C3D.

Algoritmo de redondeo completo

La tarea de construir cualquier tipo de filetes incluye varias etapas:

1. Divide la cadena dada en componentes elementales (para redondear tres caras es exactamente tres caras: izquierda, derecha y centro).
2. Organizar constantemente componentes elementales.
3. Construya una superficie de filete para cada componente elemental.
4. Coser las superficies de filete adyacentes con costillas.
5. Para procesar las secciones finales de la cadena de filete, es decir, conectarlas correctamente al cuerpo modificado.

El punto clave en este procedimiento es el tercer paso: construir una superficie de filete para tres caras dadas.

Para construir la superficie deseada, primero es necesario determinar las curvas por las cuales el filete toca cada una de las tres caras. En el caso general, estas curvas solo se pueden construir como splines que pasan por puntos conocidos que se calculan de antemano.

Considere cómo puede calcular un triple de puntos, uno en cada spline.


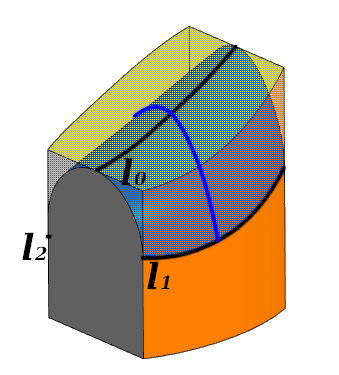Procesamiento elemental. El filete toca cada una de las tres caras a lo largo de las curvas l ₀ ; l ₁ ; l ₂ . La línea azul muestra la sección transversal.

En cada sección transversal $$$ABC$:

• $$$OA = OB = OC$- calculado automáticamente
• $$$OA, OB, OC$ortogonal a los planos tangentes de las superficies en los puntos correspondientes
• $$$p$₀ - punto de anclaje, se encuentra en el plano $$$ABC$.

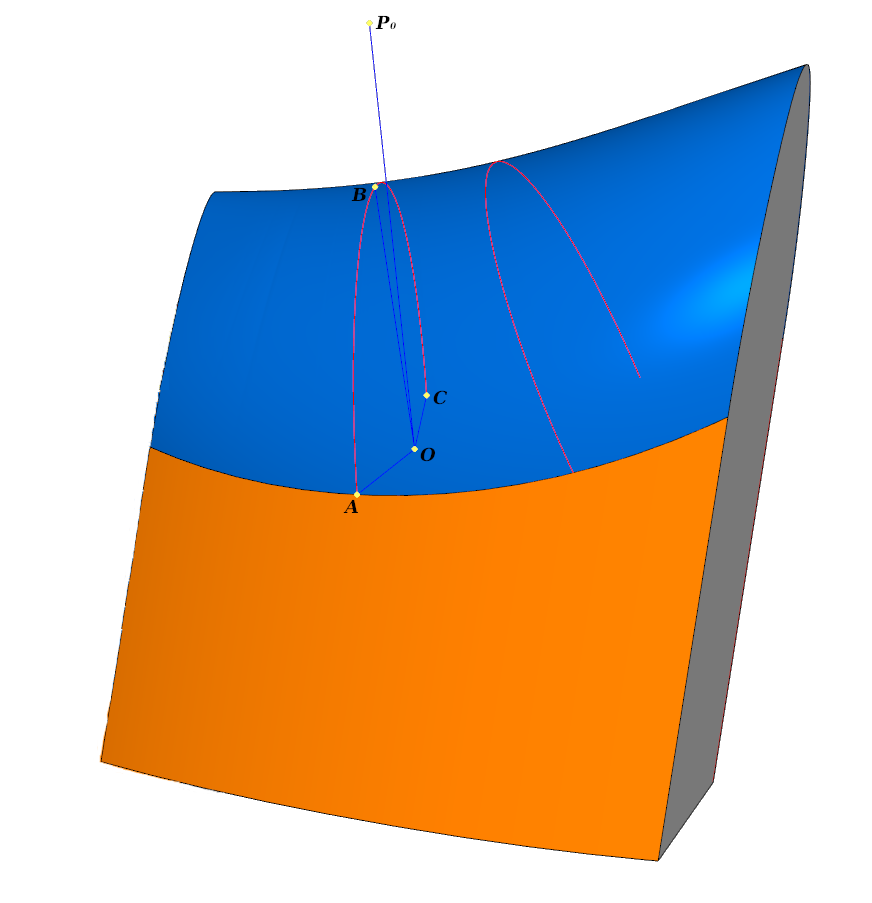
Definimos las superficies iniciales de las caras central, izquierda y derecha por vectores de radio en un cierto dominio de definición. Deje que las superficies laterales se definan por vectores de radio $$$r$₁ $$$(u, v)$y $$$r$₂ $$$(z, w)$y el central $$$r$_{0 0} $$$(x, y)$. Introducimos un parámetro numérico positivo $$$d$.

Denote por $$$n$_{0 0} $$$(x, y)$, $$$n$₁ $$$(u, v)$, $$$n$₂ $$$(z, w)$normales simples a las superficies correspondientes, dirigidas "hacia adentro".


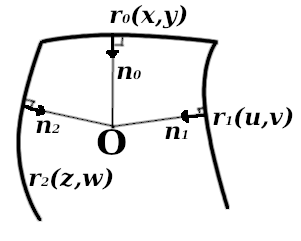Cruce la "sección" al construir un filete

Requerimos que los extremos de estas normales se estiren $$$d$veces, golpea un punto - punto $$$O$.

En términos de geometría diferencial, nuestros requisitos pueden formularse mediante un sistema de siete ecuaciones con siete parámetros:

$$$dn$_{0 0} $$$(x, y)$= $$$dn$₁ $$$(u, v)$,
$$$dn$_{0 0} $$$(x, y)$= $$$dn$₂ $$$(z, w)$,
( $$$r$_{0 0} $$$(x, y)$- $$$p$_{0 0} $$$r$₁ $$$(u, v)$- $$$p$_{0 0} $$$r$₂ $$$(z, w)$- $$$p$₀ ) = $$$0$,

donde

• $$$d$- radio variable
• $$$p$₀ - punto de anclaje
• $$$x, y, u, v, z, w$- variables del área de definición de parámetros.

Usando algoritmos de métodos numéricos (por ejemplo, el método de Newton), encontramos una solución para este sistema: $$$x$_{0 0} $$$y$_{0 0} $$$u$_{0 0} $$$v$_{0 0} $$$z$_{0 0} $$$w$_{0 0} $$$d$₀ .

La solución define puntos de contacto con superficies:

• $$$r$₀ ( $$$x$_{0 0} $$$y$₀ )
• $$$r$₁ ( $$$u$_{0 0} $$$v$₀ )
• $$$r$₂ ( $$$z$_{0 0} $$$w$₀ )

así como el radio $$$d$₀ .

Corriendo por un conjunto de puntos $$$p$₀ , obtenemos conjuntos de triples de puntos tangentes con superficies desde las cuales puede restaurar "curvas táctiles" $$$l$_{0 0} $$$l$₁ $$$l$_{2 a} medida que Hermite se divide pasando por puntos calculados.

Alcance [ $$$t$_min $$$t$_max ] todas las curvas son iguales y el parámetro $$$t$_me corresponde a un punto $$$r$_0i $$$r$_1i $$$r$_2i . Además, estas curvas se usan para calcular la sección transversal del filete deseada.

Arreglamos algunos parámetros $$$t$y calcule los puntos para ello:

• $$$r$_{0 0} $$$(x (t), y (t)),$
• $$$r$₁ $$$(u (t), v (t)),$
• $$$r$₂ $$$(z (t), w (t))$.

Construimos una curva spline que pasa por estos puntos y vectores normales ortogonales a ellos $$$n$_{0 0} $$$(x (t), y (t))$, $$$n$₁ $$$(u (t), v (t))$, $$$n$₂ $$$(z (t), w (t))$en consecuencia

Si el enunciado del problema se modifica ligeramente y se busca la curva en puntos dados y vectores tangentes en estos puntos, entonces los métodos por los cuales se puede implementar dicha spline se pueden encontrar, por ejemplo, en el libro de Nikolai Golovanov "Modelado geométrico".

El libro describe en detalle los métodos para redondear un borde del cuerpo, en particular, se muestra que la sección transversal de un redondeo se puede realizar como una curva NURBS definida por tres puntos. Si se redondean tres caras, una curva similar estará determinada por cinco puntos.

Entonces, para cada parámetro $$$t$podemos definir un conjunto de puntos para construir NURBS y, por lo tanto, definir cada punto de la sección transversal de la superficie del filete. Por lo tanto, el problema de la construcción de la superficie está completamente resuelto.

Hubo una pequeña pregunta en la descripción de esta parte del algoritmo: cómo elegir el conjunto de puntos "correctamente" $$$p$₀ correspondiente a la sección transversal a través de la cual será fácil restaurar las "curvas táctiles" $$$l$_{0 0} $$$l$₁ $$$l$₂ ?

Parece razonable tomarlos con alguna curva preseleccionada. No entraremos en los detalles de la construcción de esta curva, solo notamos que debe ser suave, sin auto intersecciones y "promedio" de las cadenas de bordes que delimitan la cara central a la izquierda y a la derecha.


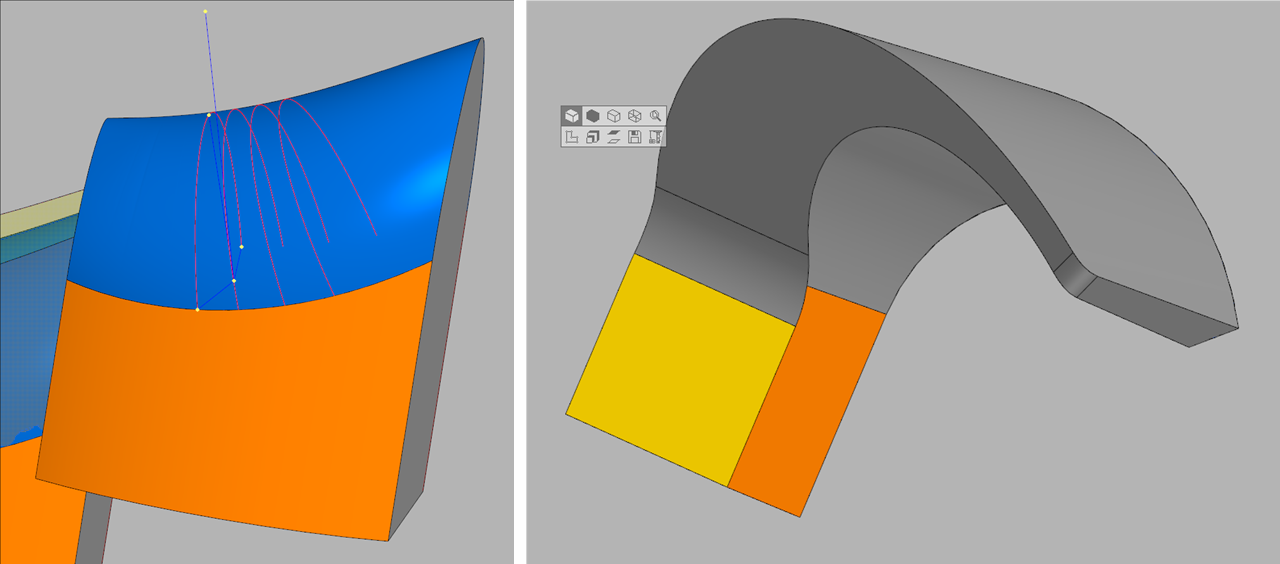Izquierda, transversal, dependiente del punto $$$p$₀ .
A la derecha, las cifras pueden ser bastante complejas, por lo que elegir la curva "auxiliar" correctamente es una tarea separada.

Ahora que somos capaces de construir superficies de filete para los casos elementales más simples, podemos pasar a un problema más complejo: construir una superficie para una cadena de caras.
El principal problema aquí es "coser" superficies adyacentes de manera suave. Este es el cuarto paso del algoritmo.

La dificultad radica precisamente en la suavidad de la reticulación, ya que las superficies se construyen con diferentes datos iniciales. Para garantizar la suavidad, uno tiene que recurrir a varios trucos: cambiar la dirección y la longitud de los vectores de derivadas en la dirección longitudinal a una cierta distancia del límite, cambiar los valores de las derivadas de las funciones de peso en los límites, etc. Los resultados son visibles en la figura: las líneas de cebra más suaves corresponden a una superficie más suave.




Arriba hay un modelo sin un algoritmo de suavizado. Abajo: después de aplicar el algoritmo.

Resumen

Como resultado de nuestra investigación, el núcleo geométrico C3D es capaz de construir una sección transversal de filete, curvas de soporte, filete de tres caras; sabe cómo suavizar la superficie eligiendo una parametrización; sabe parcialmente cómo unir suavemente las superficies de filete adyacentes.


Autor - Anna Ladilova, Ph.D., matemática / programadora C3D Labs