Cómo funciona la criptografía de curva elíptica en TLS 1.3

Un par de alertas para el lector:

Para simplificar (un poco) el proceso de descripción y ajustar el volumen del artículo que vamos a escribir, es esencial hacer un comentario significativo y establecer la restricción principal de inmediato: todo lo que vamos a decir hoy sobre la práctica El lado de la problemática es viable solo en términos de TLS 1.3. Lo que significa que, si bien su certificado ECDSA aún funcionaría en TLS 1.2 si lo desea, proporciona compatibilidad con versiones anteriores, la descripción del proceso de protocolo de enlace real, los trajes de cifrado y los puntos de referencia cliente-servidor solo cubre TLS 1.3. Por supuesto, esto no se relaciona con la descripción matemática de los algoritmos detrás de los sistemas de cifrado modernos.

Este artículo no fue escrito por un matemático ni un ingeniero, aunque ayudaron a encontrar una manera de evitar las matemáticas aterradoras y lo revisaron. Muchas gracias a los empleados de Qrator Labs.

( E líptico C urve) D iffie- H ellman ( E phemeral)

The Diffie: el legado de Hellman en el siglo XXI

Por supuesto, esto no ha comenzado ni con Diffie ni con Hellman. Pero para proporcionar una línea de tiempo correcta, necesitamos señalar fechas y eventos principales.

Hubo varias personas importantes en el desarrollo de la criptografía moderna. En particular, Alan Turing y Claud Shannon hicieron una increíble cantidad de trabajo sobre el campo de la teoría de la computación y la teoría de la información, así como sobre el criptoanálisis general, y tanto Diffie como Hellman, son acreditados oficialmente por tener la idea de la clave pública. (o la llamada criptografía asimétrica) (aunque se sabe que en el Reino Unido se hicieron avances serios en la criptografía que permanecieron en secreto durante mucho tiempo), convirtiendo a esos dos caballeros en pioneros.

¿En que exactamente?

Bueno, esto puede sonar peculiar; sin embargo, antes del 6 de noviembre de 1976, no había conocimiento público de los sistemas de cifrado de clave pública. Whitfield Diffie y Martin Hellman (y, de hecho, Ralph Merkle): matemáticos, ingenieros informáticos y entusiastas, así como criptólogos fueron los primeros.

Para aquellos que no lo saben, debido al papel que desempeñó el criptoanálisis durante la Segunda Guerra Mundial y su enorme impacto en mantener la información en secreto, los dos países que creían que tenían el conocimiento más avanzado en criptografía, los EE. UU. Y el Reino Unido incluyeron el cifrado en sus listas de municiones y aprovecharon una fuerte prohibición de exportación (debilitando simultáneamente la implementación de cifrado para uso privado, privado y comercial). Por esta razón, los investigadores del Reino Unido que trabajan en la técnica de intercambio de claves asimétricas en la sede de comunicaciones gubernamentales y desarrollan un esquema análogo no fueron reconocidos para esta invención hasta 1997, cuando las restricciones en los algoritmos de criptografía y su descripción se volvieron ineficaces.

Volviendo a nuestros inventores duales, ¿qué han revolucionado Diffie y Hellman específicamente?

Echemos un vistazo a su trabajo original, que ilustra perfectamente el salto gigante que han introducido (incluso teóricamente con su trabajo de investigación):

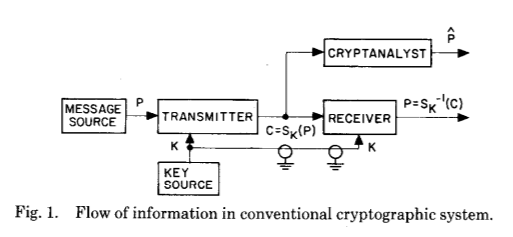
Y el siguiente:

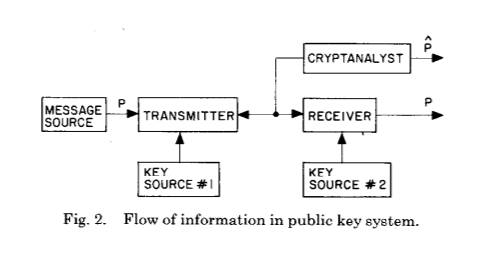
Estas dos imágenes ilustran perfectamente el gran cambio que Whitfield Diffie y Martin Hellman introdujeron después de siglos de evolución de criptografía y criptoanálisis: el establecimiento de una clave secreta compartida como resultado de un cálculo criptográfico.

Echemos un vistazo a otra buena foto con colores:



Explica lo que está pasando. Antes de la invención del acuerdo de clave de Diffie y Hellman, solo había una clave simétrica: se usaba para cifrar y descifrar el mensaje. Si desea darle a alguien esa "clave", debe transferirse a través de un canal "seguro". Puede imaginar de inmediato todas las restricciones de un esquema de generación anterior de este tipo: necesita un canal seguro ya establecido, no puede reutilizar la clave e, idealmente, la longitud de la clave debe ser la misma que la longitud del mensaje.

Claude Shannon en su obra clasificada en tiempos de guerra " Teoría de la comunicación de los sistemas de secreto " demostró que todos los cifrados teóricamente irrompibles deben tener los mismos requisitos que el código único, conocido como el cifrado Vernam, por el autor de este cifrado simétrico de flujo polialfabético.

Nuevamente, vamos a echar un vistazo al artículo original:


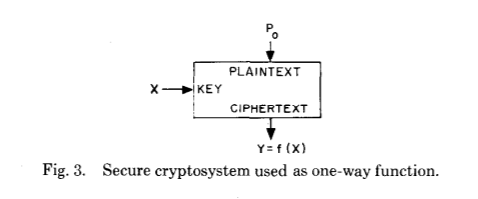
Antes de continuar, preguntémonos: ¿cómo dos, aunque brillantes, sin embargo, los seres humanos obtuvieron una mejora tan significativa en un campo aplicado con tal historia, especialmente en el momento de la guerra?
Bueno, por el:

• Teoría de la información , formulada por Claude Shannon;
• Teoría de la computación influenciada, en particular, por Alonzo Church, John von Neumann y Alan Turing;
• Y, lo que es más importante, la teoría de la computabilidad se basa principalmente en el trabajo de Turing, que podríamos decir que todo se desarrolló y maduró en el mismo período del siglo XX. Diffie y Hellman mencionaron a Claude Shannon como el influyente más significativo de su trabajo.

La " seguridad universal " de Lenstra ilustra la cantidad de energía necesaria para "romper" el sistema criptográfico simétrico con varias longitudes clave. Resultó que romper una clave de curva elíptica de 228 bits de largo requeriría la misma cantidad de energía que se necesita para hervir toda el agua en la Tierra. Sin embargo, es válido solo bajo la consideración de algoritmos y hardware conocidos, ya que, estrictamente hablando, nadie sabe si existen algoritmos o hardware significativamente más eficientes. La clave EC de 228 bits es comparable a la clave RSA de 2380 bits, más sobre eso más adelante. Aunque en esta estimación, las claves RSA y EC se utilizan en un esquema de cifrado asimétrico, tales longitudes de clave son algo equivalentes a una clave de cifrado simétrico de 128 bits.

Es fácil imaginar que algo "difícil de calcular" requeriría mucha energía y / o tiempo necesario para el cálculo. Tendemos a pensar que las computadoras pueden "calcular todo", pero resulta que no es cierto. Primero, existen ejemplos indecidibles, como el problema de detención, aunque en el campo de la criptografía, podemos evitar esta trampa. En segundo lugar, si consideramos el tiempo necesario para que se ejecute un algoritmo en particular, puede ser arbitrariamente alto. Eso es lo que explotamos en criptografía. Un problema se considera "fácil" de calcular si el tiempo requerido para ejecutar el algoritmo respectivo depende del tamaño de entrada (medido en bits) como un polinomio:$$ $ en línea $ T (n) = O (n ^ k) $ en línea $ , para alguna constante positiva$$ $ en línea $ k $ en línea $ . En el campo de la teoría de la complejidad computacional , tales problemas forman la clase de complejidad P.

La clase de complejidad P es casi central, ya que representa el problema para el cual existe un algoritmo de tiempo polinómico determinista. Otra clase de complejidad es el NP (los problemas que son "difíciles" de calcular), que representan un conjunto de problemas de decisión, es decir, problemas que requieren una respuesta "sí" o "no", que tienen una prueba verificable en tiempo polinómico. ¿Ves la palabra "prueba" aquí? Ahí es donde llegamos a las funciones de trampillas, que pertenecen a la clase de complejidad NP.


Créditos: xkcd

Funciones unidireccionales; Funciones de trampillas

Por definición, una función unidireccional es una función que es fácil de calcular en cada entrada pero es difícil de revertir, es decir, calcular la entrada original dada solo la salida. "Fácil" y "difícil" se refieren a las definiciones de la teoría de la complejidad computacional anteriores. Curiosamente, la existencia de funciones unidireccionales no está probada (matemáticamente) porque su existencia probaría que las clases de complejidad P y NP no son iguales, mientras que P igual NP o no es hoy un problema abierto. Por lo tanto, tenga en cuenta que toda la criptografía moderna se basa en hipótesis no comprobadas.

Ahora, en su artículo original, Diffie y Hellman presentan otra generación de las funciones unidireccionales que llamaron "funciones de puerta trampa". ¿Cómo se diferencian?
Como explican en su documento histórico:

En un criptosistema de clave pública, el cifrado y el descifrado se rigen por claves distintas, E y D, de modo que calcular D a partir de E es computacionalmente inviable (por ejemplo, requiere$$ $ en línea $ 10 ^ {100} $ en línea $ instrucciones). La clave de cifrado E se puede revelar [en un directorio] sin comprometer la clave de descifrado D. Esto permite que cualquier usuario del sistema envíe un mensaje a cualquier otro usuario cifrado de tal manera que solo el destinatario previsto pueda descifrarlo. .. El problema de la autenticación es quizás una barrera aún más grave para la adopción universal de las telecomunicaciones para las transacciones comerciales que los problemas de distribución de claves ... [it] ... está en el corazón de cualquier sistema que implique contratos y facturación.

Por convención, los caracteres de criptografía "Alice" y "Bob" (que buscan una comunicación segura) se utilizan con frecuencia para explicar el concepto de clave pública. Alice y Bob acuerdan enteros grandes$$ $ en línea $ n $ en línea $ y$$ $ en línea $ g $ en línea $ con$$ $ en línea $ 1 <g <n $ en línea $ . La selección impacta la seguridad del sistema. "El módulo$$ $ en línea $ n $ en línea $ debería ser primo; mas importante$$ $ en línea $ (n-1) / 2 $ en línea $ también debe ser un primo <...> y$$ $ en línea $ g $ en línea $ debería ser un módulo raíz primitivo$$ $ en línea $ n $ en línea $ <...> [y]$$ $ en línea $ n $ en línea $ debe tener <...> al menos 512 bits de largo ”. El protocolo Diffie - Hellman se puede establecer en forma elemental en 5 pasos.

1. Alice elige$$ $ en línea $ x $ en línea $ (un gran número entero aleatorio) y calcula$$ $ en línea $ X = g ^ x \ bmod n $ en línea $
2. Bob elige$$ $ en línea $ y $ en línea $ (un gran número entero aleatorio) y calcula$$ $ en línea $ Y = g ^ y \ bmod n $ en línea $
3. Alice envía$$ $ en línea $ X $ en línea $ a Bob, mientras Bob envía$$ $ en línea $ Y $ en línea $ a Alice (guardan$$ $ en línea $ x $ en línea $ y$$ $ en línea $ y $ en línea $ secreto el uno del otro)
4. Alice calcula$$ $ en línea $ k = Y ^ x \ bmod n $ en línea $
5. Bob calcula$$ $ en línea $ k '= X ^ y \ bmod n $ en línea $

Como resultado, Alice y Bob tienen el mismo valor.$$ $ en línea $ k = k '$ en línea $ eso sirve como un secreto compartido.

La función de trampilla es una función unidireccional que hace posible encontrar su inverso si uno tiene una información especial llamada "trampilla". Suena fácil, aunque fue bastante difícil encontrar tales funciones: el primer método factible se encontró en la implementación de un algoritmo de cifrado asimétrico de criptografía de clave pública llamado RSA en honor a sus creadores: Ron Rivest, Adi Shamir y Leonard Adleman.

RSA

En RSA, la dureza de invertir la función se basa en el hecho de que la factorización (encontrar multiplicadores primos de un número) lleva mucho más tiempo que la multiplicación, o deberíamos decir aquí que ningún método de tiempo polinómico para factorizar números enteros grandes en una computadora clásica tiene encontrado, sin embargo, no se ha demostrado que no exista ninguno.

En RSA, como en cualquier otro sistema de cifrado de clave pública, hay dos claves: pública y privada. RSA toma el mensaje de entrada (representado como una cadena de bits) y le aplica una operación matemática (módulo de exponenciación un número entero grande) para obtener un resultado que se ve indistinguible de aleatorio. El descifrado toma este resultado y aplica una operación similar para recuperar el mensaje original. En la criptografía asimétrica, el cifrado se realiza con la clave pública y el descifrado con la clave privada.

Como? Porque los operandos pertenecen a un grupo cíclico finito (un conjunto de enteros con multiplicación en aritmética modular). Las computadoras no se manejan muy bien con números arbitrariamente grandes, pero, afortunadamente, nuestro grupo cíclico de enteros es realizar una operación llamada "ajuste": un número mayor que el máximo permitido se ajusta a un número en el rango válido que operamos . Esto nos permite operar con teclas de "no más de" longitud. En la criptografía de curva elíptica, también se usan grupos cíclicos (multiplicativos), pero se construyen de manera un poco diferente, como veremos más adelante.

Básicamente, lo que hace RSA es tomar dos números primos grandes y multiplicarlos para obtener el llamado módulo. Todos los otros números a tratar residen entre cero y el módulo. El módulo debe ser parte de la clave pública, y su longitud de bits determina la longitud de la clave. La segunda parte de la clave pública es un número elegido entre cero y el totient de Euler (la implementación moderna de RSA toma el totient de Carmichael en lugar del Euler) del módulo con algunas restricciones adicionales. Finalmente, la clave privada debe calcularse resolviendo alguna ecuación modular. Para cifrar un número, simplemente lo elevamos a la potencia igual a la clave pública, y para descifrar un número, lo elevamos a la potencia igual a la clave privada. Gracias a la naturaleza cíclica del grupo, recuperamos el número inicial.

Hay dos problemas importantes con el RSA hoy en día, uno es consecuencia del otro. A medida que crece la longitud de una clave (es decir, el número de sus bits), el factor de complejidad no crece tan rápido como cabría esperar. Esto se debe a que existe un algoritmo de factorización sub-exponencial (pero aún súper polinomial ). Por lo tanto, para mantener un nivel de seguridad adecuado, la longitud de la clave RSA debe crecer algo más rápido que la longitud de la clave ECC. Es por eso que las claves RSA más extendidas en la actualidad tienen una longitud de 2048 o 3072 bits.

Un poco más tarde, veremos en números cómo la longitud de la clave afecta la eficiencia general del sistema criptográfico al comparar el certificado RSA y ECDSA firmado con la autoridad Let's Encrypt.

(Célvica elíptica) D igital S ignature A lgorithm

La búsqueda de una mejor función de trampilla eventualmente llevó a los criptógrafos a una rama de las matemáticas de mediados de los 80 dedicada a las curvas elípticas.

Sería la tarea final describir la criptografía de curva elíptica en un artículo, por lo que no lo haremos. En cambio, echemos un vistazo a una función de trampilla de curva elíptica basada en el problema de logaritmo discreto.

Hay muchos iniciadores y más introducciones en profundidad en la criptografía de curva elíptica, y recomendamos especialmente "ECC: una introducción suave" de Andrea Corbellini si está interesado en las matemáticas.

Lo que nos interesa son parámetros bastante "simples".

La curva elíptica se define mediante una ecuación como esta:$$ $ en línea $ y ^ 2 = x ^ 3 + ax + b $ en línea $
Dicha curva es necesaria para construir un subgrupo cíclico sobre un campo finito. Por lo tanto, se están utilizando los siguientes parámetros:

• La prima$$ $ en línea $ p $ en línea $ que especifica el tamaño del campo finito;
• Los coeficientes$$ $ en línea $ a $ en línea $ y$$ $ en línea $ b $ en línea $ de la ecuación de curva elíptica;
• El punto base$$ $ en línea $ g $ en línea $ eso genera el subgrupo mencionado;
• El orden$$ $ en línea $ n $ en línea $ del subgrupo;
• El cofactor$$ $ en línea $ h $ en línea $ del subgrupo.

En conclusión, los parámetros de dominio para nuestros algoritmos son el sextuplet$$ $ en línea $ (p, a, b, G, n, h) $ en línea $ .
Dichas curvas elípticas funcionan sobre el campo finito.$$ $ en línea $ \ mathbb {F} _p $ en línea $ donde$$ $ en línea $ p $ en línea $ es un número primo bastante grande. Entonces tenemos un conjunto de módulos enteros$$ $ en línea $ p $ en línea $ , donde las operaciones, como la suma, resta, multiplicación, inversa aditiva, inversa multiplicativa son posibles. La suma y la multiplicación funcionan de manera similar a la aritmética modular o llamada "reloj" que vimos en las "envolturas" de RSA.
Dado que la curva es simétrica respecto al eje x, dado cualquier punto$$ $ en línea $ P $ en línea $ podemos tomar$$ $ en línea $ −P $ en línea $ ser el punto opuesto Tomamos$$ $ en línea $ −O $ en línea $ para ser justo$$ $ en línea $ O $ en línea $ .
La suma de puntos de curva se define de una manera que los puntos dados$$ $ en línea $ P $ en línea $ y$$ $ en línea $ Q $ en línea $ , podemos dibujar líneas que intersectan esos puntos y la curva de intersección en un tercer punto$$ $ en línea $ R $ en línea $ para que$$ $ en línea $ P + Q = -R $ en línea $ y$$ $ en línea $ P + Q + R = 0 $ en línea $ .

Echemos un vistazo a la explicación de Marc Hughes :

Arriba se muestra una línea de pendiente constante que viaja a lo largo de la superficie del toro. Esta línea pasa a través de dos puntos enteros seleccionados al azar en la curva.



Para agregar dos puntos en el gráfico, dibuje una línea desde el primer punto seleccionado$$ $ en línea $ P $ en línea $ hasta el segundo punto seleccionado$$ $ en línea $ Q $ en línea $ y extienda la línea hasta que se cruce con otro punto en el gráfico$$ $ en línea $ -R $ en línea $ , extendiéndolo a través de los límites de la trama si es necesario.

Una vez que intercepte un punto entero, refleje el punto verticalmente a través del centro del gráfico (una línea de puntos anaranjada) para encontrar el nuevo punto$$ $ en línea $ R $ en línea $ en el gráfico Por lo tanto$$ $ en línea $ P + Q = R $ en línea $ .

La multiplicación por un escalar ahora es trivial:$$ $ en línea $ n \ cdot P = P + P + P + \ dots + P $ en línea $ (aquí están$$ $ en línea $ n $ en línea $ sumandos).

La función de trampilla aquí se encuentra dentro del problema del logaritmo discreto (para curvas elípticas), no de la factorización que analizamos en la sección RSA. El problema es: si sabemos$$ $ en línea $ P $ en línea $ y$$ $ en línea $ Q $ en línea $ que es tal$$ $ en línea $ k $ en línea $ que$$ $ en línea $ Q = k \ cdot P $ en línea $ ?

Se supone que tanto el problema de factorización (subyacente al RSA) como el logaritmo discreto para curvas elípticas (que es la base de ECDSA y ECDH) son difíciles, es decir, no hay algoritmos conocidos para resolver este problema en tiempo polinómico para una clave dada longitud

Si bien, normalmente, cualquier persona se avergonzaría de mezclar el intercambio de claves (ECDH) con el algoritmo de firma (ECDSA), debemos explicar cómo funcionan juntos. Un certificado TLS moderno contiene una clave pública, en nuestro caso, del par de claves generado por el algoritmo de curva elíptica, generalmente firmado por una autoridad de nivel superior. El cliente verifica la firma del servidor y obtiene el secreto compartido. El secreto compartido se utiliza en un algoritmo de cifrado simétrico, como AES o ChaCha20. Sin embargo, el principio sigue siendo el mismo: acuerde los parámetros del dominio (el sextuplet), obtenga el par de claves, donde la clave privada es un entero seleccionado al azar (el multiplicando de$$ $ en línea $ Q = k \ cdot P $ en línea $ ), y la clave pública es un punto en la curva. Los algoritmos de firma usan el punto base$$ $ en línea $ g $ en línea $ , que es un generador para un subgrupo de orden primo grande$$ $ en línea $ n $ en línea $ tal que$$ $ en línea $ n \ cdot G = 0 $ en línea $ , donde 0 es el elemento de identidad. La firma prueba que la conexión segura se está estableciendo con la parte auténtica: un servidor que tiene el certificado TLS (clave pública) firmado por alguna autoridad de certificación para el nombre del servidor dado.

(EC) DH (E) + ECDSA = Forma actual de apretón de manos

En el TLS moderno (1.3), el cliente y el servidor generan su par de claves pública-privada sobre la marcha, mientras establecen la conexión, esto se denomina versión efímera del intercambio de claves. Las bibliotecas TLS de navegador más populares lo admiten. En su mayoría, utilizan la curva elíptica Edwards 25519 , introducida por Daniel J. Bernstein (djb), que ofrece seguridad de 128 bits. Desde 2014 openssh usa esta curva para la creación del par de claves. Sin embargo, en 2019, los navegadores aún no admiten sesiones TLS con servidores que tengan un certificado con clave pública EdDSA.

Pero volvamos a cómo funcionan las cosas a fines de 2019 con TLS 1.3.

Los mecanismos de intercambio de claves en TLS 1.3 están restringidos a (EC) basados ​​en DH (E) (con el x25519 es compatible con las bibliotecas TLS del lado del cliente de los navegadores más populares, así como las bibliotecas TLS del lado del servidor, como OpenSSL, que inspeccionaremos un poco más tarde), y la lista del conjunto de cifrado contiene solo tres entradas: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 y TLS_CHACHA20_POLY1305_SHA256. Para aquellos de ustedes que saben cómo se nombraron los conjuntos de cifrado en la versión TLS 1.2, es evidente de inmediato que el mecanismo de intercambio de claves ahora está "separado" del nombre del conjunto de cifrado, también se eliminaron los modos de intercambio estático RSA y Diffie estático - Hellman de la especificación por completo. Incluso la reanudación de la sesión basada en PSK se realiza a través de ECDHE en TLS 1.3. También es cierto para los parámetros personalizados de DH, que ahora no están permitidos, dejando solo aquellos generalmente aceptados como seguros en la especificación del protocolo final.

Es interesante que haya una diferencia bastante significativa en cómo funcionan los algoritmos de cifrado asimétrico en la actualidad. Con ECC (y los certificados ECDSA en particular) utilizamos claves más pequeñas para llegar a niveles de seguridad "convenientes", en comparación con RSA. Eso permite el uso de un algoritmo de cifrado asimétrico más fuerte y mecanismos de intercambio de claves en dispositivos más pequeños y, a veces, incluso en cosas que generalmente no se consideran un dispositivo (tarjeta inteligente).

En primer lugar, es necesario mencionar lo que significa "criptosistema híbrido" en términos de TLS 1.3.
Un criptosistema híbrido es el que utiliza el cifrado asimétrico (clave pública) para establecer un secreto compartido, que luego se utiliza como clave en una secuencia simétrica o cifrado de bloque.

En segundo lugar, infraestructura de clave pública y certificados. Es interesante que en su entrevista de 2004 Martin Hellman mencionó a un "héroe no reconocido" Loren Kohnfelder, cuya tesis de licenciatura del MIT introdujo una estructura de árbol de lo que ahora conocemos como infraestructura de clave pública. Sin embargo, volvamos a los certificados.

El hecho de que el servidor realmente tenga la clave privada está garantizado por su firma, que se puede verificar con la clave pública del servidor. Y el certificado asegura que alguna clave pública pertenece a un servidor específico. Significa que está estableciendo una comunicación segura con la parte específica y no con un impostor. Tu banco, no un cibercriminal. En TLS 1.3 hay una mejora significativa sobre el formato de negociación anterior: el servidor firma toda la información que tiene hasta este momento: el saludo del cliente y el saludo del servidor, incluido el cifrado negociado. Echemos un vistazo a la sección correspondiente del RFC 8446 :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

En TLS 1.3, el cliente envía la clave compartida (junto con los parámetros necesarios), algoritmos de firma de inmediato en el primer mensaje (Client Hello). Las claves necesarias para intercambiar con el servidor se crean en segundo plano, sin que el usuario lo note. Se intercambian aún más con el servidor para crear un secreto común, a partir de claves secretas pre-master que se establecieron cuando el servidor envió su mensaje (Server Hello) respondiendo al cliente.
En el lado "Server Hello" puede ver que el Certificado * se transfiere al cliente, junto con la parte Certificado Verificación * que verifica que la parte posee la clave privada para la entrada de clave pública correspondiente, y crea la clave de sesión (simétrica) si todo sale según lo planeado, lo que significa que el lado que solicita los datos (cliente) verificó con éxito el lado que responde (servidor), creando aún más un secreto común.

Hay dos operaciones esenciales ocultas en estas transmisiones: creación de firma y verificación de firma. Estos se realizan en ambos lados de la comunicación, ya que la "firma" es esencialmente una prueba de que la parte realmente tiene la clave privada correspondiente a la clave pública, que los datos provienen del firmante y el mensaje no fue alterado en tránsito.

Con RSA, como veremos más adelante, la operación de firma es la más costosa. Como estamos firmando con una clave larga de 2048 o 3072 bits, dicha operación carga el servidor significativamente, mucho más de lo que carga al cliente verificando dicha firma.

Con ECDSA, tenemos claves más pequeñas (vamos a ver el ECDSA con NIST P-256 (o el secp256v1)) pero operaciones más complejas. Como resultado, podría verse como el RSA "al revés": el cálculo de verificación de firma carga más al cliente, mientras que el servidor maneja fácilmente la creación de la firma. Las mediciones verifican eso, vea la sección "Un poco de referencia".

Este efecto escala fácilmente Internet hoy en día, ya que los clientes modernos son casi igual de poderosos que los servidores (teniendo en cuenta solo la frecuencia central de la CPU), por lo que podrían llevar a la práctica la costosa operación. El servidor, a su vez, puede usar las capacidades liberadas para crear más firmas y establecer más sesiones.

Encriptemos la firma del certificado

Entonces, para proporcionar al lector un poco de instrucciones prácticas y prácticas sobre cómo crear un servidor habilitado para TLS con el par de claves ECDSA firmado por la autoridad Let's Encrypt, decidimos ilustrar un proceso completo de creación de un par de claves necesario para crear una CSR (solicitud de firma de certificado) para Let's Encrypt y, como resultado, obtener el certificado ECDSA necesario para nuestro servidor.

Tenemos que generar una clave privada para continuar. Utilizaremos la biblioteca OpenSSL.
El manual de OpenSSL describe la generación de cualquier tecla EC a través de un comando especial, designado especialmente para la rama de la curva elíptica del algoritmo de generación.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

Para verificar que la biblioteca OpenSSL hizo todo bien, podemos ejecutar el comando ec .

 openssl ec -in privatekey.pem -noout -text 

La salida nos mostrará la curva especificada con la que se ha creado la clave.

El siguiente paso es bastante esencial para la creación de la CSR: para omitir el proceso de completar todos los detalles de información necesarios para obtener el certificado, necesitamos el archivo de configuración. Afortunadamente, Mozilla hizo todo el trabajo por nosotros, presentando el " Generador de configuración SSL ". Allí, puede elegir entre las opciones de servidor disponibles. La configuración pura de OpenSSL, peculiarmente no presente en la página del generador, se vería así:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

Nota: no es necesario tener el CNF; si no lo hace, se le solicitará que complete estos detalles en la línea de comando.

Ahora, siga la creación de una CSR en sí. Aquí tenemos un útil comando OpenSSL.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

También podemos verificar la corrección de una CSR recién creada.

 openssl req -in csr.pem -noout -text -verify 

Aquí hemos llegado a una fase final: usar un cliente ACME, certbot, para pasar nuestra solicitud de firma de certificado a Let's Encrypt.

Certbot lo ayuda a obtener el certificado necesario y tiene muchas opciones. Aquí dijo, si eres nuevo en el cifrado de clave pública y la infraestructura PKI que tenemos en 2019, es mejor que uses --dry-run antes de intentar obtener el certificado para cualquier dominio tuyo.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

En este caso, el cliente certbot verifica que la lista de dominios solicitados (en la línea de comando) coincida con los dominios enumerados en la solicitud de firma de certificado. En el --dns-somednsprovider miente un poco, porque hay muchas maneras en que puedes probar Let's Encrypt que estás en posesión de una parte particular del tráfico de Internet. Sin embargo, si está utilizando algún proveedor de alojamiento en la nube pública, digamos DigitalOcean, Hetzner, Amazon, Azure, cualquier cosa, probablemente habría una forma más natural de proporcionar la información necesaria, porque su proveedor ya creó alguna herramienta de integración.

Después, si está seguro de la exactitud de los parámetros que está utilizando para pasar su CSR a Let's Encrypt a través de un cliente certbot, excluya el parámetro --dry-run de su comando y continúe.

Si tiene éxito, el cliente produciría varios certificados como salida: el certificado firmado en sí, los certificados raíz e intermedios, y la combinación de estos últimos como la cadena de certificados nombrada por última vez, todo en el formato de archivo .pem.

OpenSSL tiene un comando que podríamos usar para inspeccionar los certificados:

 openssl x509 -in chainfilepath.pem -noout -text 

En este punto, se hace evidente que Let's Encrypt firmó el certificado utilizando el resumen SHA256. Además, la firma de ECDSA Root and Intermediates se incluye en la sección "Próximas funciones", lo que significa que en este momento solo obtendría intermedios de RSA. Pero está bien, ya que todavía está utilizando la clave pública ECDSA.

Al final de esta sección, nos gustaría decir algo en relación con la longitud de las teclas. En seguridad de la información, es común decir que el nivel de seguridad es 2 ^ x, donde x es la longitud de bits (RSA es una pequeña excepción aquí, ya que crece un poco más lento que exponencialmente). Para aproximar cómo las teclas utilizadas para diferentes algoritmos se corresponden entre sí, nos referiremos a la página wiki de OpenSSL.
Como puede ver, las diferencias son bastante prominentes. Aunque con Let's Encrypt no pudimos obtener ningún certificado firmado fuera de las claves de curva elíptica 256 (secp256v1) y 384 (secp384r1).

Problemas conocidos y excepciones, y LA NSA

Créditos: xkcd

Probablemente, el tema central del uso de la criptografía de curva elíptica a través de los años fue la necesidad de un generador de números aleatorios cuidadosamente diseñado, para crear claves del nivel de seguridad requerido.

Hubo un escándalo masivo alrededor del algoritmo Dual_EC_DRBG (generador de bits aleatorio determinista de curva elíptica dual), que tardó muchos años en resolverse. Además, existe incertidumbre acerca de las patentes ECC, ya que se sabe que muchas de ellas pertenecían a la empresa Certicom, que fue adquirida por Blackberry. También hay compañías que están certificadas para el uso de ECC de Blackberry. Por supuesto, existe una desconfianza simple en algunas normas del NIST, que podría verse afectada o no por la NSA o cualquier otra institución de vigilancia y cumplimiento de los Estados Unidos.

El lado de la implementación de un problema es una pregunta completamente diferente. En 2010, la consola PlayStation 3 sufrió una recuperación de clave privada de Sony debido a la implementación inadecuada del algoritmo ECDSA: tenían un estático aleatorio que hacía que la función de trampilla tuviera solución. OpenSSL también sufrió en el año siguiente, sin embargo, corrigió rápidamente la vulnerabilidad que permitía la recuperación de una clave privada con la ayuda de un ataque de tiempo, para obtener más información, consulte el documento original .

En 2013, en la conferencia RSA, un grupo de investigadores presentó su " ¡Falló al azar! Documento sobre las vulnerabilidades de la clase Java SecureRandom. Medio año después, se redujo a las billeteras de Android Bitcoin , creadas usando PRNG criptográficamente seguro insuficiente.

Debido a serias vulnerabilidades en serie descubiertas, en el mismo agosto de 2013, IETF lanzó un RFC 6979 , que describe una generación determinista de k utilizada en la creación de claves. Podríamos decir que tal medida solucionó el problema, pero no lo haremos, en cualquier momento los investigadores podrían encontrar problemas en numerosas implementaciones debido a una desviación innecesaria de las especificaciones del protocolo.

Sobre la NSA. Si no ha escuchado sobre la historia de Dual_EC_DRBG: reserve algo de tiempo y lea los artículos correspondientes, no se arrepentirá de entrar en detalles. Edward Snowden es parte de esta historia porque las revelaciones de 2013 probaron las sospechas anteriores. Como resultado, muchos criptógrafos prominentes perdieron la confianza en el NIST, ya que esa organización diseñó y describió muchas de las curvas y otros algoritmos, subyacentes a ECDSA.

La curva 25519 de Daniel Bernstein y la función DH es la respuesta a estos dos problemas y, como describimos anteriormente, una transición hacia EdDSA es lenta pero evidente. Incluso con las curvas NIST, todavía no se ha encontrado evidencia de su vulnerabilidad y, como ya hemos mencionado, la experiencia relacionada con el azar ha sido bastante instructiva.

Para concluir esta parte, queremos dar la cita de John von Neumann: "Cualquiera que intente generar números aleatorios por medios deterministas está, por supuesto, viviendo en un estado de pecado".

Un poco de referencia

Utilizamos un servidor NGINX 1.16.0 con OpenSSL 1.1.1d para ejecutar estos puntos de referencia con varios certificados. Como mencionamos anteriormente, actualmente Let's Encrypt solo permite los algoritmos prime256v1 y secp384r1 para las solicitudes de firma de certificados, y no proporciona certificados ECDSA raíz e intermedios, probablemente trabajando en esta característica al momento de escribir este artículo.
Como puede ver, para un solo núcleo de la CPU Intel® Xeon® Silver 4114 @ 2.20GHz (lanzado Q3'17), la diferencia general en el rendimiento de ECDSA, en comparación con el ampliamente adoptado RSA 2048 es 3.5x.

Ahora echemos un vistazo a los resultados de velocidad de OpenSSL del mismo procesador con ECDSA y RSA.
Aquí podemos ver una confirmación de la tesis dada anteriormente de los diferentes costos computacionales para el signo y verificar las operaciones de ECC y RSA. Como resultado, actualmente equipado con TLS 1.3 ECC proporciona un aumento significativo del rendimiento en el nivel de seguridad de bit más alto, en comparación con RSA. Esa es la razón más importante por la que en Qrator Labs alentamos a nuestros clientes a adoptar ECDSA. Con las CPU modernas, obtienes casi la diferencia de 5 veces a favor de ECDSA.

Si está interesado en cómo su CPU realiza cálculos criptográficos, puede ejecutar un simple comando de openssl speed . Los -rsa , -ecdsa y -eddsa le darían resultados de referencia para los algoritmos de firma correspondientes.

(Superpuesto) Futuro

Créditos: djb

Es irónico que mientras estábamos preparando este artículo, Google anunció " alcanzar la supremacía cuántica ". ¿Significa esto que estamos en peligro en este momento y que todo lo desarrollado hasta este momento no proporciona ningún secreto?

Pues no.

Como Bruce Schneier escribió en su ensayo para IEEE Security and Privacy " Criptografía después de las tierras de los extraterrestres ", se podría hacer un gran golpe con una computadora cuántica lo suficientemente potente como para la criptografía de clave pública (asimétrica). La criptografía simétrica seguiría siendo fuerte.

Queremos citar a Bruce Schneier con lo siguiente:

Hay un escenario futuro más a considerar, uno que no requiere una computadora cuántica. Si bien hay varias teorías matemáticas que sustentan la unidireccionalidad que utilizamos en la criptografía, probar la validez de esas teorías es, de hecho, uno de los grandes problemas abiertos en la informática. Así como es posible que un criptógrafo inteligente encuentre un nuevo truco que facilite romper un algoritmo en particular, podríamos imaginar extraterrestres con suficiente teoría matemática para romper todos los algoritmos de encriptación. Para nosotros, hoy, esto es ridículo. La criptografía de clave pública es una teoría de números y es potencialmente vulnerable a los extraterrestres con mayor inclinación matemática. La criptografía simétrica es tanto un embrollo no lineal, tan fácil de hacer más complejo y tan fácil de aumentar la longitud de la clave, que este futuro es inimaginable. Considere una variante AES con un bloque de 512 bits y un tamaño de clave, y 128 rondas. A menos que las matemáticas sean fundamentalmente diferentes de nuestra comprensión actual, eso será seguro hasta que las computadoras estén hechas de algo diferente a la materia y ocupen algo que no sea el espacio.

Pero si sucede lo inimaginable, eso nos dejaría con una criptografía basada únicamente en la teoría de la información: los pads únicos y sus variantes.

Esta es el área donde, excepto en busca de fallas de implementación, se pueden encontrar la mayoría de los problemas. Si hay un grupo de matemáticos, criptoanalistas / criptógrafos e ingenieros informáticos bien financiados que trabajan para probar o refutar algunos problemas matemáticos complejos extraordinarios (como el P? = NP) y lograr resultados sustanciales hasta este momento, podríamos estar en problemas. Sin embargo, es poco probable que tales avances en ciencias de la computación, información y teorías de computabilidad se oculten, ya que ese hecho escribiría los nombres de sus creadores en las páginas de Historia y, específicamente, los libros de texto de Historia de Internet, lo que no tiene precio para cualquiera que sea inteligente . Por lo tanto, tal escenario podría considerarse casi imposible.

No está claro si en los próximos 5 años habría algún éxito con la computación cuántica, aunque ya hay varias primitivas de criptografía consideradas adecuadas para el mundo post-cuántico: retículas, curvas elípticas supersingulares basadas en isogenia, hashes y códigos. Por ahora, los especialistas en seguridad solo están experimentando con ellos. Sin embargo, no hay duda de que, en caso de necesidad, la humanidad emplearía rápidamente dichos algoritmos a gran escala.

Por ahora, la criptografía basada en la curva elíptica parece ser perfecta para la década futura, ya que proporciona seguridad y rendimiento.